经典边界条件黏弹性Pasternak地基上Bernoulli-Euler梁横向自振特性分析
2021-01-16付艳艳余云燕
付艳艳, 余云燕
(兰州交通大学 土木工程学院, 兰州 730070)
土木工程中的许多工程构件,诸如铁道轨枕、公路路面,隧道中用以增强地基承载力的梁,在对它们进行动力分析时均可简化为地基梁模型[1-4]。而结构的自振特性又是反映结构动力特性的重要物理量,在结构安全性及可靠性评价时具有重要的意义,因此地基梁的动力特性在学术界及工程领域也备受关注。
Bernoulli-Euler梁在梁理论的发展历史上有着非常重要的地位,由于其理论形式简单易用,并且在很多问题上都能给出可以接受的工程近似解答,故而在以往对地基梁的研究中多有应用。Ge等[5]研究了Winkler地基上含有空腔的Bernoulli-Euler的自振频率和模态;彭丽等[6]运用复模态方法研究了有限长黏弹性Winkler 地基上的Bernoulli-Euler梁的振动特性,得出简支边界条件下的复频率方程和复模态函数表达式。马建军等[7~8]基于Winkler地基模型、Euler梁理论,研究了考虑土体质量及有限深度土体运动影响的有限长地基梁的线性和非线性固有频率及模态构型。彭丽等[9-10]应用复模态方法研究了Pasternak地基上不同边界条件下的Bernoulli-Euler梁的自振特性数值解及任一初始激励条件下外激励的响应。丁虎等[11]由共振关系给出Pasternak地基上两端简支和两端固支边界条件下Bernoulli-Euler梁的固有频率以及模态。此外,由于Pasternak地基模型考虑了地基梁与地基之间剪切作用,能够更精确的模拟地基土体的力学性质。因此,近年来关于黏弹性Pasternak地基梁自振特性的研究成果也颇多。Wang等[12]研究了Pasternak地基上各种经典边界条件下的Timoshenko梁的自振频率近似解,并给出具体算例分析了转动惯量、剪切模量和地基参数对梁自振频率的影响。彭丽等[13]应用复模态方法研究了Pasternak 地基上Timoshenko梁的自振特性。Zhang等[14]通过差值矩阵法研究了在保守轴向压缩力下黏弹性Pasternak地基上锥形截面Timoshenko梁的横向自振特性。虽然在以上的研究中对黏弹性Pasternak地基与Bernoulli-Euler梁的组合也有所涉及,但却非常有限,且这些研究对各种经典边界条件的分析较为分散,尚不够全面。
回传射线矩阵法(MRRM)计算精度高、计算速度快、数值稳定性好,在结构的自振特性研究中已有一定的应用[15-19],但在这些研究中对结构模态的研究仅停留在实部范围内。故本文基于回传射线矩阵法(MRRM),在复数域内对黏弹性Pasternak地基上的Bernoulli-Euler梁在两端简支、两端自由、两端固支、简支-自由、简支-固支及固支-自由这六种边界条件下的横向自振特性进行研究。建立各边界条件下的回传射线矩阵,推导得到各边界条件下的频率方程;根据边界条件及正交归一化条件进一步求解出模态函数解析表达式。通过具体算例验证自振频率及衰减系数解析表达式的正确性,分析不同边界条件下的自振频率、衰减系数及模态。为黏弹性地基梁的振动特性研究提供理论基础。
1 振动控制方程及方程的解
黏弹性Pasternak地基上Bernoulli-Euler梁的力学模型及坐标系如图1所示。
对黏弹性Pasternak地基上的Bernoulli-Euler梁进行节点编号,如图1所示,分别在节点1及节点2处建立局部坐标系x12及x21,若以l表示梁长,则两者的关系为x12=l-x21。整体坐标系x的方向与局部坐标系x12一致。其横向自由振动控制方程为
(1)
式中:ρ、A、I分别表示梁体的材料密度、横截面面积和横截面对其形心主轴的惯性矩;E为梁体材料杨氏模量;k1、k2、β分别为土体的弹性系数、剪切系数和阻尼系数;v为梁的挠度;t为时间。

图1 黏弹性Pasternak 地基上Bernoulli-Euler梁的力学模型及坐标系
对式(1)进行无量纲化,令
(2)
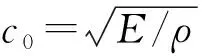
将式(2)代入式(1),并整理得:
(3)
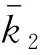
(4)
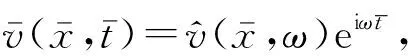
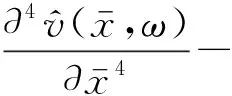
(5)
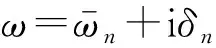
求解式(5)得:
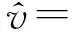
(6)
其中,aj(ω)为入射波波幅,dj(ω)为出射波波幅,λj为波数,其表达式为
j=1,2
(7)
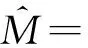
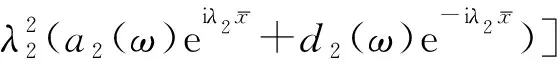
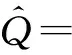
(8)
2 经典边界条件下的自振频率及模态函数
分别考虑两端简支、两端自由、两端固支、简支-自由、简支-固支及固支-自由六种边界条件下的自振频率和模态函数,其节点耦合条件如表1所示。

表1 经典边界条件下黏弹性Pasternak地基上Euler-Bernoulli梁的节点耦合条件
2.1 两端简支边界条件下的自振频率和模态函数
以两端简支为例,基于回传射线矩阵法推导其频率方程及模态函数,将式(6)及式(8)代入表1中两端简支的节点耦合条件中,可得:
(9)
对式(9)进行整理并合并为
d=S1a
(10)
式中:a和d表示总体入射波波幅向量和总体出射波波幅向量;S1为两端简支边界条件下黏弹性Pasternak地基上Bernoulli-Euler梁的总体散射矩阵。其表达式分别为
(11)
由于出射波波幅向量和入射波波幅之间存在如下的相位关系
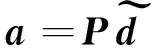
(12)
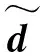
(13)
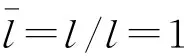
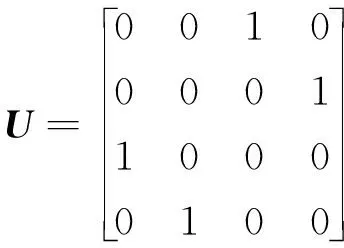
(14)
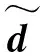
a=PUd
(15)
将式(15)代入式(10)中并整理得
[I-R]d=0
(16)
式中,R=S1PU称为两端简支边界条件下黏弹性Pasternak地基上Euler-Bernoulli梁的回传射线矩阵。
要使式(16)中的d有非零解,则其系数行列式为零,得到两端简支边界条件下黏弹性Pasternak地基上的Bernoulli-Euler梁的频率方程为
(17)
将式(9)转化到单一局部坐标系x12得
(18)
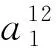
(19)
则两端简支边界条件下的模态函数表达式为
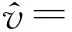
(20)
根据指数函数与三角函数及双曲函数的关系
(21)
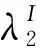
2.2 其它边界条件下的自振频率和模态函数
2.2.1 两端自由边界条件下的自振频率及模态函数
|I-S2PU|=(1-e-2iλ1)(1-e-2iλ2)-
(22)
式中,除了总体散射矩阵S2外,其余各矩阵都与两端简支边界条件下相同,S2的表达式为
(23)
两端自由边界条件下的模态函数表达式为
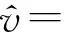
(24)
2.2.2 两端固支边界条件下的自振频率及振动模态
两端固支边界条件下黏弹性Pasternak地基上的Euler-Bernoulli梁的频率方程为
|I-S3PU|=(1-e-2iλ1)(1-e-2iλ2)-
(25)
式中,S3的表达式为
(26)
两端固支边界条件下的模态函数表达式为
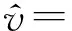
(27)
对比式(22)、式(25) 及式(24) 、式(27)可知,两端固支与两端自由边界条件下的黏弹性Pasternak地基上的Bernoulli-Euler梁的频率方程完全相同,而其相应的振动模态函数却不同。
2.2.3 简支-自由边界条件下的自振频率及振动模态
简支-自由边界条件下黏弹性Pasternak地基上的Bernoulli-Euler梁的频率方程为
|I-S4PU|=(1-e-2iλ1)(1+e-2iλ2)+
(28)
式中,S4的表达式为
(29)
简支-自由边界条件下的模态函数表达式为
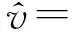
(30)
2.2.4 简支-固支边界条件下的自振频率及振动模态
简支-固支边界条件下黏弹性Pasternak地基上的Bernoulli-Euler梁的频率方程为
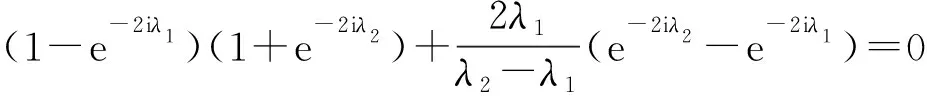
(31)
式中,S5的表达式为
S5=
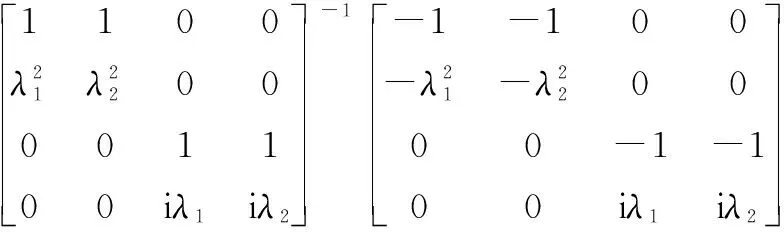
(32)
简支-固支边界条件下的模态函数表达式为
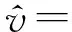
(33)
对比式(28)、式(31) 及式(30) 、式(33)可知,简支-自由与简支-固支边界条件下的黏弹性Pasternak地基上的Bernoulli-Euler梁的频率方程亦完全相同,而其相应的振动模态函数却不同。
2.2.5 固支-自由边界条件下的自振频率及振动模态
固支-自由边界条件下黏弹性Pasternak地基上的Euler-Bernoulli梁的频率方程为
|I-S6PU|=(1-e-2iλ1)(1-e-2iλ2)-
(34)
式中,S6的表达式为
(35)
固支-自由边界条件下的模态函数表达式为
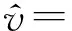
(36)
对比各边界条件下的频率方程,可以看出,两端简支边界条件下的频率方程为完全因式分解式,而其他边界条件下的频率方程不能进行完全因式分解;两端固定及两端自由边界条件下频率方程完全相同,其表达式较两端简支边界条件下多一项;简支自由和简支固定边界条件下的频率表达式也完全相同,亦是两项之和,而固定自由边界条件下的频率方程是三项之和,它又较两端固定(两端自由)的频率方程表达式多了一项。
3 模态函数正交性及其归一化条件
令
(37)
可将式(5)转化为
(38)
根据式(38)进一步可得
(39)
(40)
式中:下标m和n分别代表m阶和n阶自振频率所对应的物理量。
式(40)减去式(39),可以得到
(41)
当m≠n时,ωm≠ωn,则得到地基梁的模态函数正交性条件为
(42)
当m=n时,ωm=ωn,则可得到归一化条件为
(43)
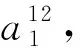
4 算例分析
通过具体算例可直观分析各经典边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的自振频率及模态函数,将用回传射线矩阵法求得的解与参考文献[20]用复模态法所得的解进行对比,考察回传射线矩阵法求解黏弹性Pasternak 地基上的Bernoulli-Euler梁的横向自振频率的正确性。Bernoulli-Euler梁及黏弹性Pasternak地基的各项物理参数如表2和表3所示。

表2 Bernoulli-Euler梁的各项物理参数

表3 黏弹性Pasternak 地基的各项物理参数
4.1 两端简支黏弹性Pasternak 地基上Bernoulli-Euler梁的自振特性解析解
4.1.1 自振频率及衰减系数
式(17)为一完全因式分解式,可以方便求解出其精确解析解。利用三角函数与指数函数的关系,将式(17)化为三角函数的形式为
|I-S1PU|=(1-cos 2λ1+isin 2λ1)(1-cos 2λ2+isin 2λ2)=0
(44)
忽略其奇异解λ1=0,因其对应的是刚体运动,其它的根为
λ1=nπ,n=1,2,3…
(45)
根据式(7),解得:
(46)
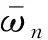
(47)
(48)
(1) 参数对自振频率及衰减系数的影响
由式(46)~(47)可知,两端简支边界条件下黏弹性Pasternak地基上Bernoulli-Euler梁的衰减系数大小与阶数n无关,仅与地基阻尼系数及梁体的尺寸有关;自振频率的大小与阶数n、地基参数和梁体参数都有关。自振频率随弹簧系数和剪切系数的增大而增大,而剪切系数对自振频率的影响大于弹簧系数;阻尼系数的增大会使自振频率减小。
(2) 自振频率及衰减系数的解析解及结果验证
根据式(47)~(48)可准确的求解出两端简支边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的衰减系数和自振频率的解析解,其结果分别如式(49)及表4所示,并将其与复模态方法求得的数值解进行对比。
(49)
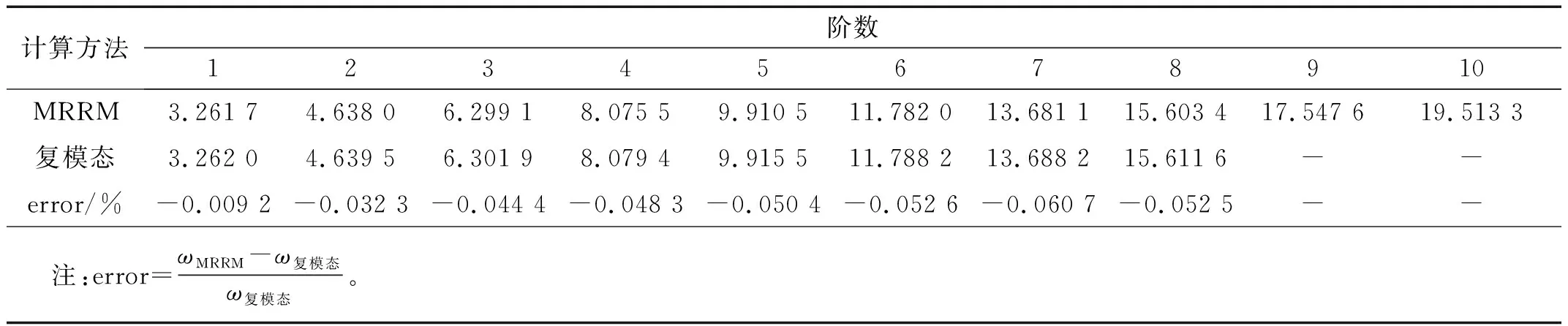
表4 两端简支Pasternak 地基上Bernoulli-Euler梁的前10阶自振频率
采用复模态方法求得的两端简支边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的衰减系数为0.05,与式(49)的结果十分接近。
由表4可知,采用回传射线矩阵法求得的黏弹性Pasternak 地基上两端简支的Bernoulli-Euler梁的自振频率解析解与复模态求得数值解基本一致,其偏差均在0.1%以内,由此也表明采用回传射线矩阵法计算自振频率方法可行。而解析解为精确解,说明复模态方法求得的数值解偏大,与精确解有一定的误差。此处解析解的提出既减少了数学编程软件编程的耗时,又能简单方便、合理可靠的计算出地基梁的自振特性,为黏弹性地基梁的振动特性的研究提供了理论基础。
4.1.2 模态函数
根据式(43)及式(47),可得
(50)
将式(21)代入式(50)中得
(51)
其中
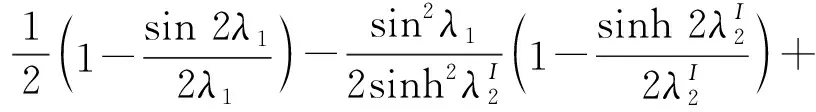
(52)
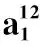
表5 两端简支黏弹性Pasternak 地基上Bernoulli-Euler梁前10阶模态函数待定参数的值(×10-4)
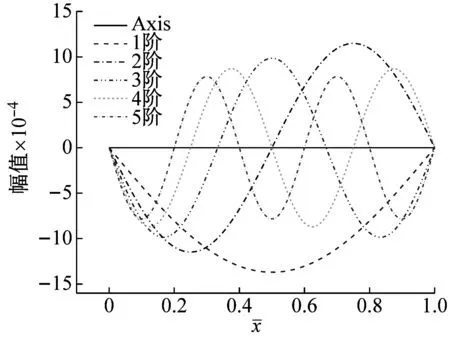
(a) 1~5阶实部
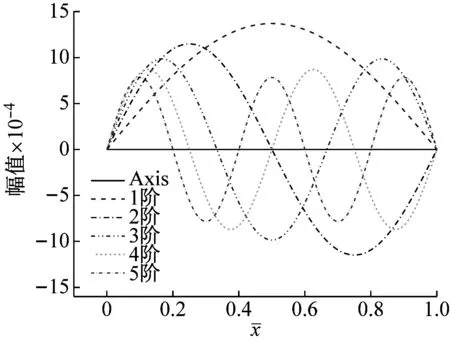
(b) 1~5阶虚部
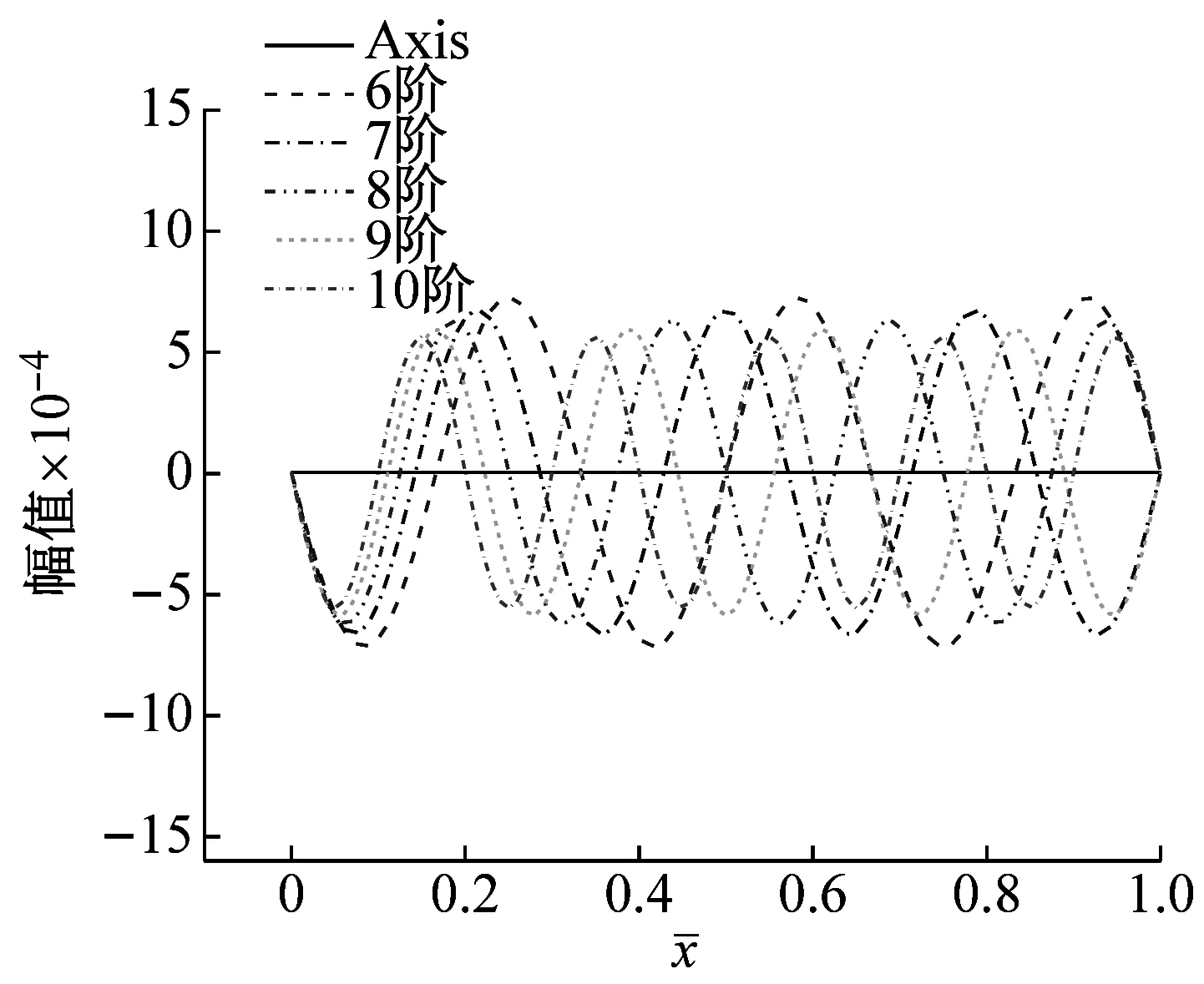
(c) 6~10阶实部
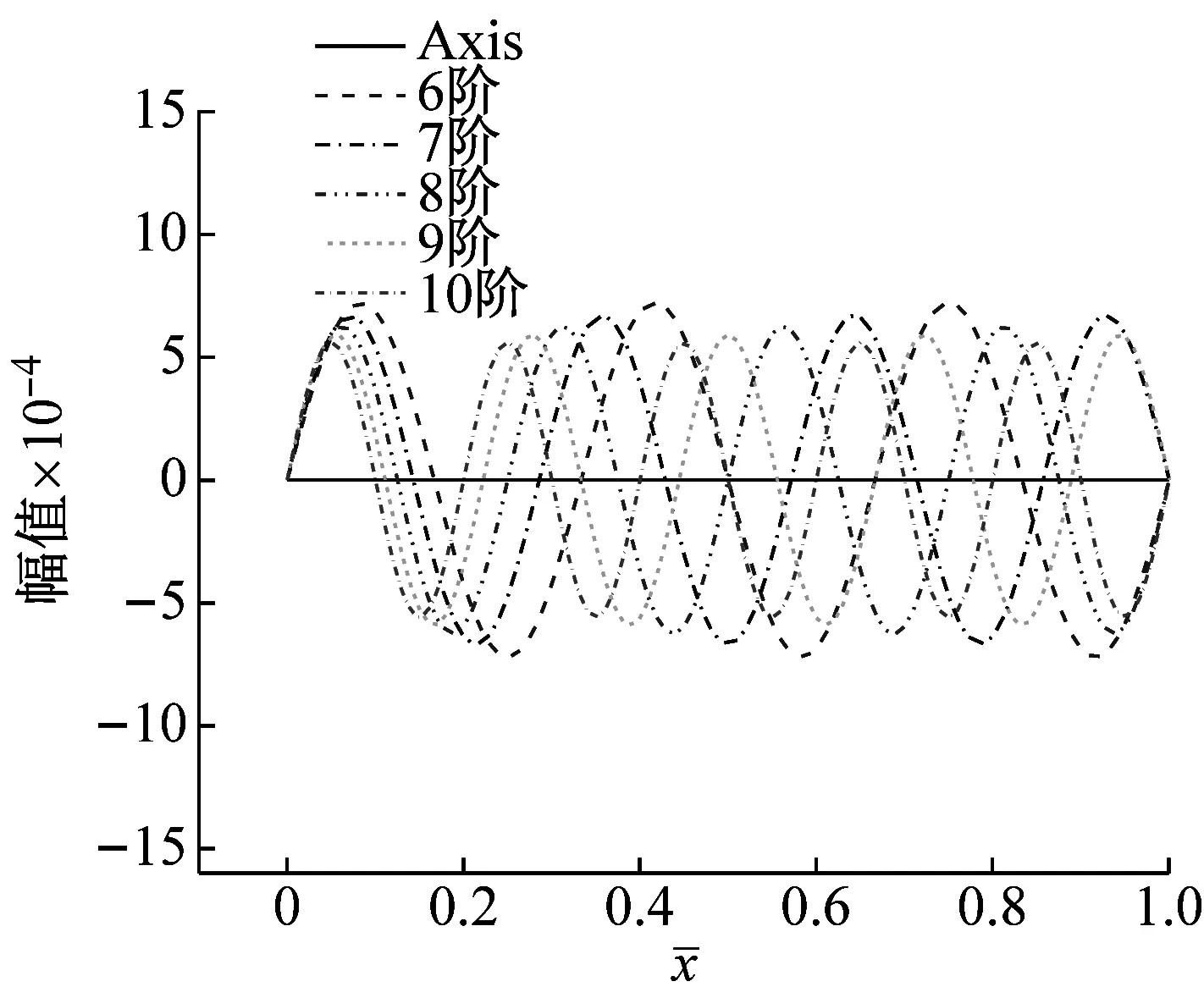
(d) 6~10阶虚部
由图2可知,两端简支边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁各阶模态曲线的实部与虚部关于轴线对称,其振幅随着阶数的增加而逐渐减小,相邻阶数幅值的减量亦随着阶数的增加而逐渐减小。
4.2 其它边界条件下Pasternak 地基上的Bernoulli-Euler梁的自振特性数值解
4.2.1 自振频率及衰减系数
通过Matlab语言编程,求解出除两端简支外的其它边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的各阶衰减系数均约等于0.049 94,与两端简支边界条件下的几乎完全相同,说明黏弹性Pasternak 地基对于Bernoulli-Euler梁振动能量的作用是一个确定的值,仅与地基土特性及梁尺寸有关,而与其上结构的约束情况无关。
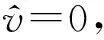
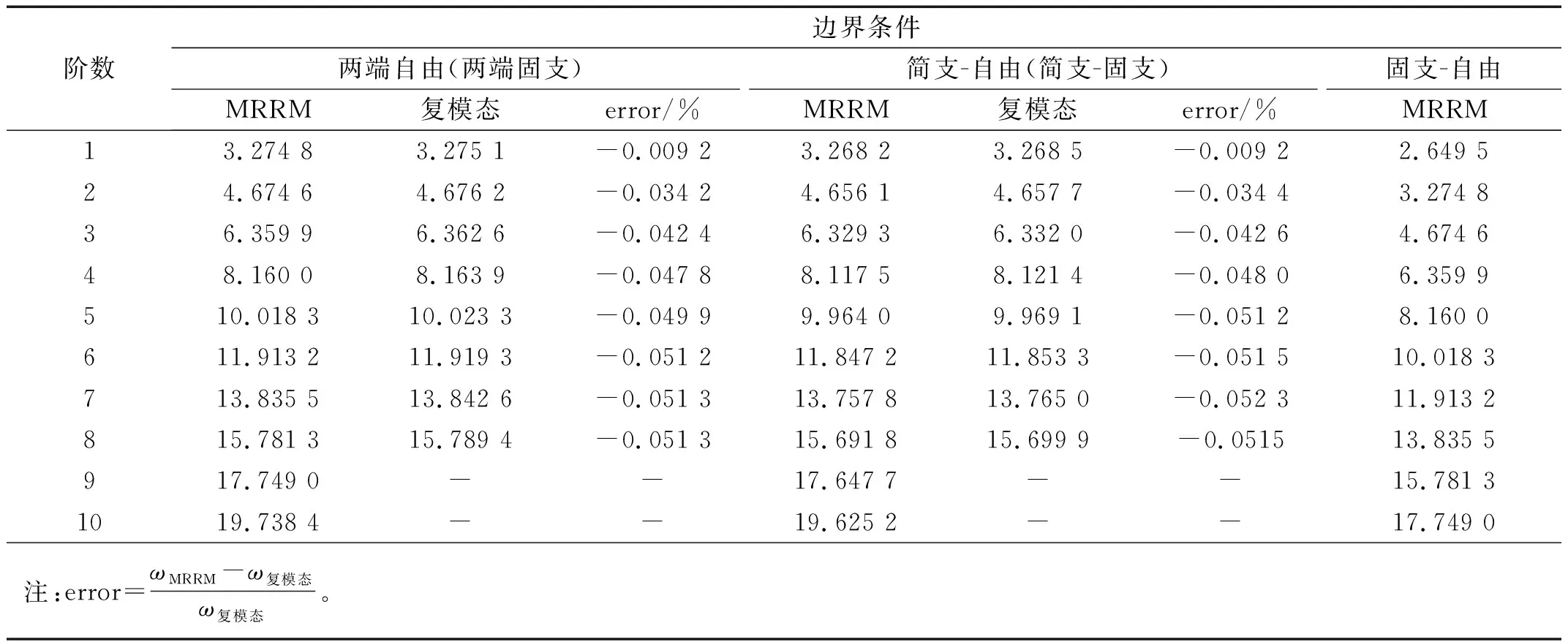
表6 其他边界条件下Pasternak 地基上Bernoulli-Euler梁的前10阶自振频率
由表6可知:
(1) 采用回传射线矩阵法求得的黏弹性Pasternak 地基上两端固支(两端自由)及简支-固支(简支-自由)边界条件下Bernoulli-Euler梁的自振频率与复模态求得结果基本一致,其偏差均在0.1%以内,进一步证明了回传射线矩阵法求解自振频率的正确性。
(2) 六种经典边界条件下黏弹性Pasternak 地基上Bernoulli-Euler的前10阶自振频率从大到小依次排序为:两端固支(两端自由)>简支-固支(简支-自由)>两端简支>固支-自由。
(3) 其他五种边界条件下Pasternak 地基上Bernoulli-Euler的前10阶自振频率的变化规律与两端简支边界条件下基本相同。且从第2阶自振频率开始,固支-自由边界条件下第n阶自振频率与两端固支(两端自由)边界条件下的第n-1阶自振频率几乎相同,说明随着阶数的增大,固支-自由边界条件下频率方程中较两端固支(两端自由)边界条件下多出的一项对自振频率的影响几乎可以忽略。
4.2.2 模态函数
经过计算可知各阶模态函数的实部与虚部关于轴线对称,故图3中仅绘出了其他5种边界条件下Pasternak 地基上Bernoulli-Euler梁前3阶模态函数曲线的实部,如图3所示。其振幅变化规律与两端简支边界条件下的变化规律基本相同。
5 结 论
基于回传射线矩阵法,首先,得到了横向自由振动时两端简支、两端自由、两端固支、简支-自由、简支-固支和固支-自由这六种边界条件下黏弹性Pasternak地基上Bernoulli-Euler梁的自振频率方程及模态函数表达式,其形式较以往研究得到的表达式更加简洁,且更容易看出不同边界条件之间的关联与差异。对其进行求解,得到两端简支边界条件下黏弹性Pasternak地基上Bernoulli-Euler梁横向自由振动时自振特性的解析解及其它边界条件下的数值解。为统一起见,根据正交归一化条件对模态函数中的未知参数进行求解。通过具体算例,对六种经典边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的自振频率、衰减系数及模态函数进行了分析,结果表明:
(1) 两端简支边界条件下黏弹性Pasternak地基上Bernoulli-Euler梁的自振频率的大小与阶数n、地基参数和梁体参数都有关,自振频率随弹簧系数和剪切系数的增大而增大,而剪切系数对自振频率的影响大于弹簧系数;阻尼系数的增大会使自振频率减小。
(2) 六种经典边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的自振频率的大小随阶数n的增长而增大;不同边界条件下自振频率从大到小依次排序为:两端固支(两端自由)>简支-固支(简支-自由)>两端简支>固支-自由。从第2阶自振频率开始,固支-自由边界条件下的第n阶自振频率与两端固支(两端自由)边界条件下的第n-1阶自振频率相同。
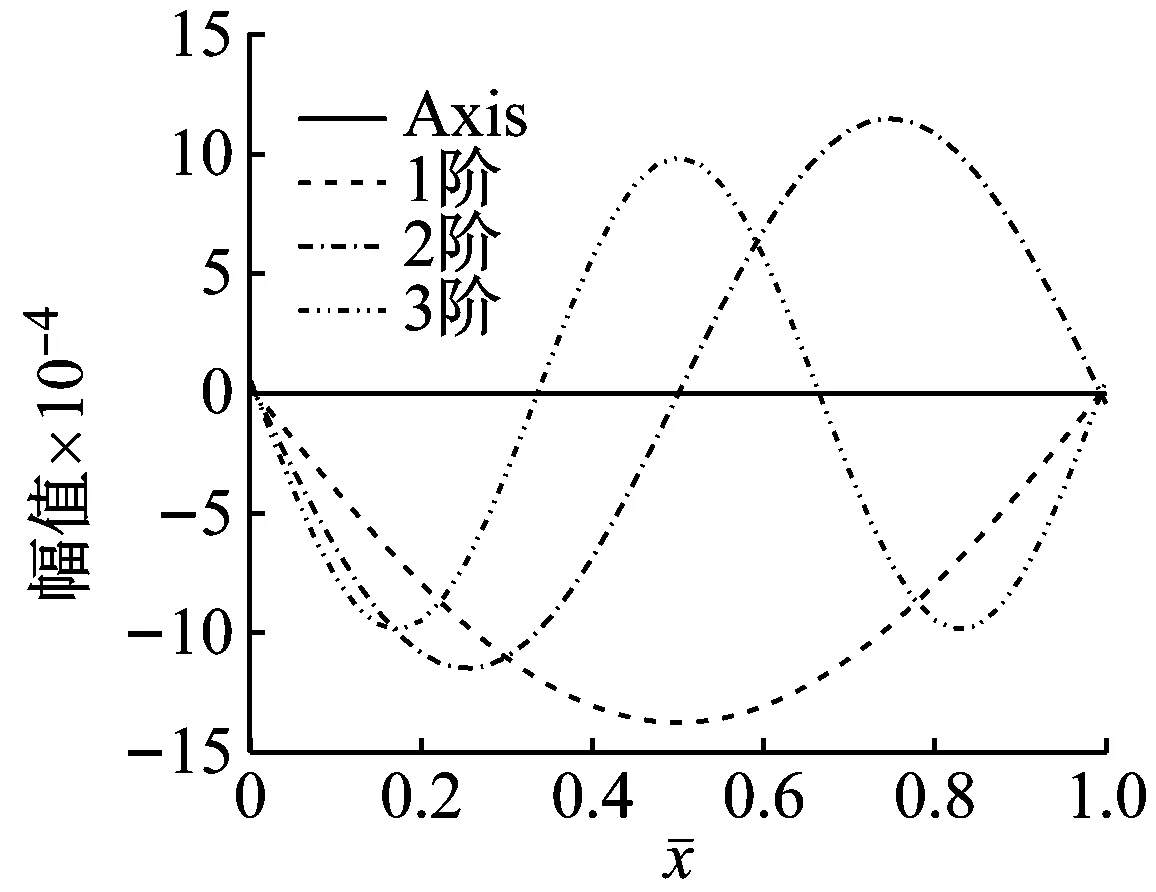
(a) 两端自由
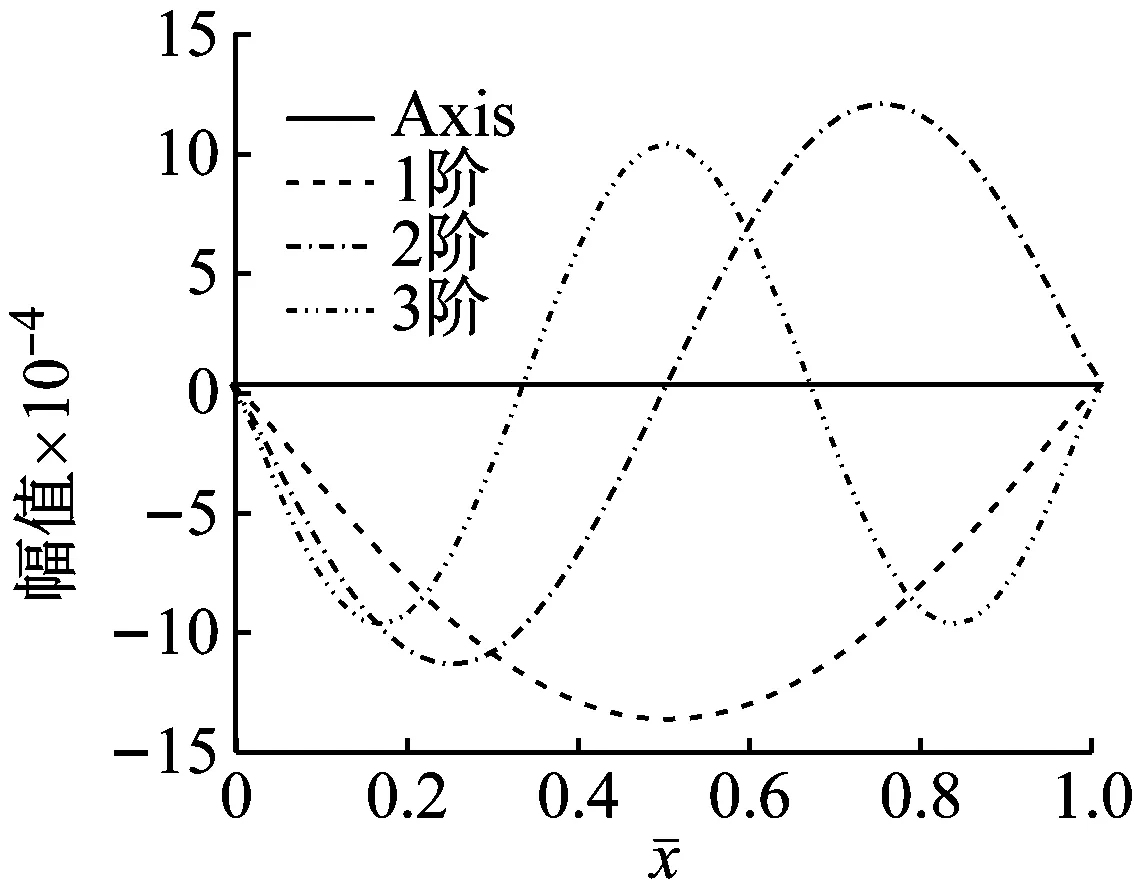
(b) 两端固支
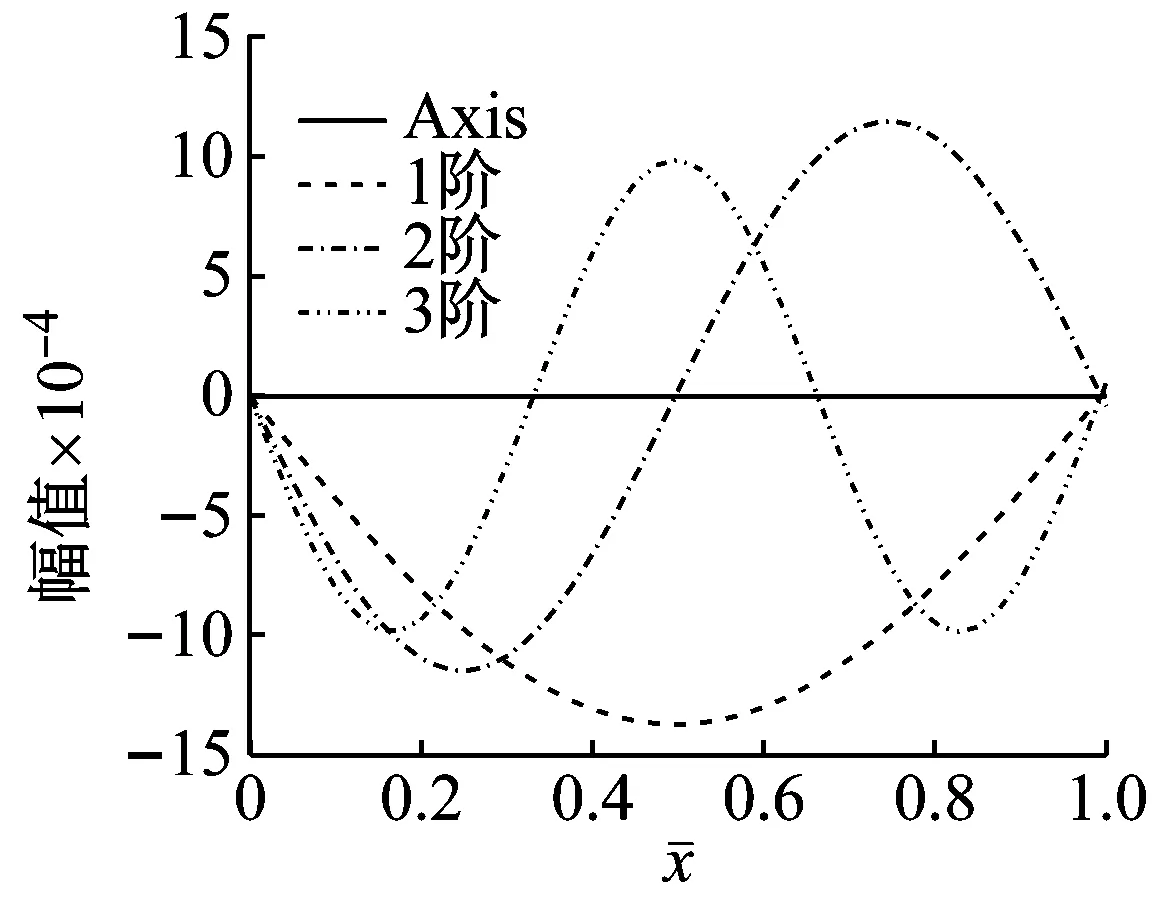
(c) 简支-自由
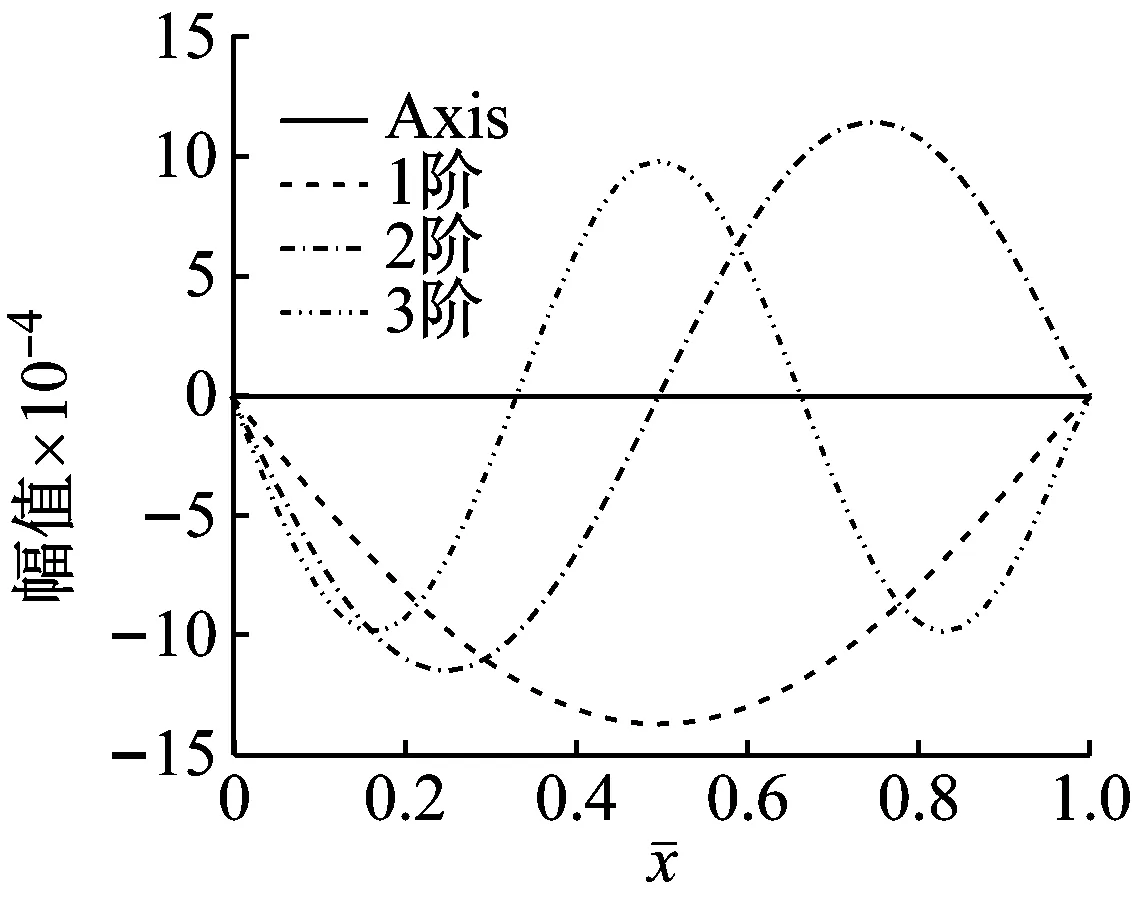
(d) 简支-固定
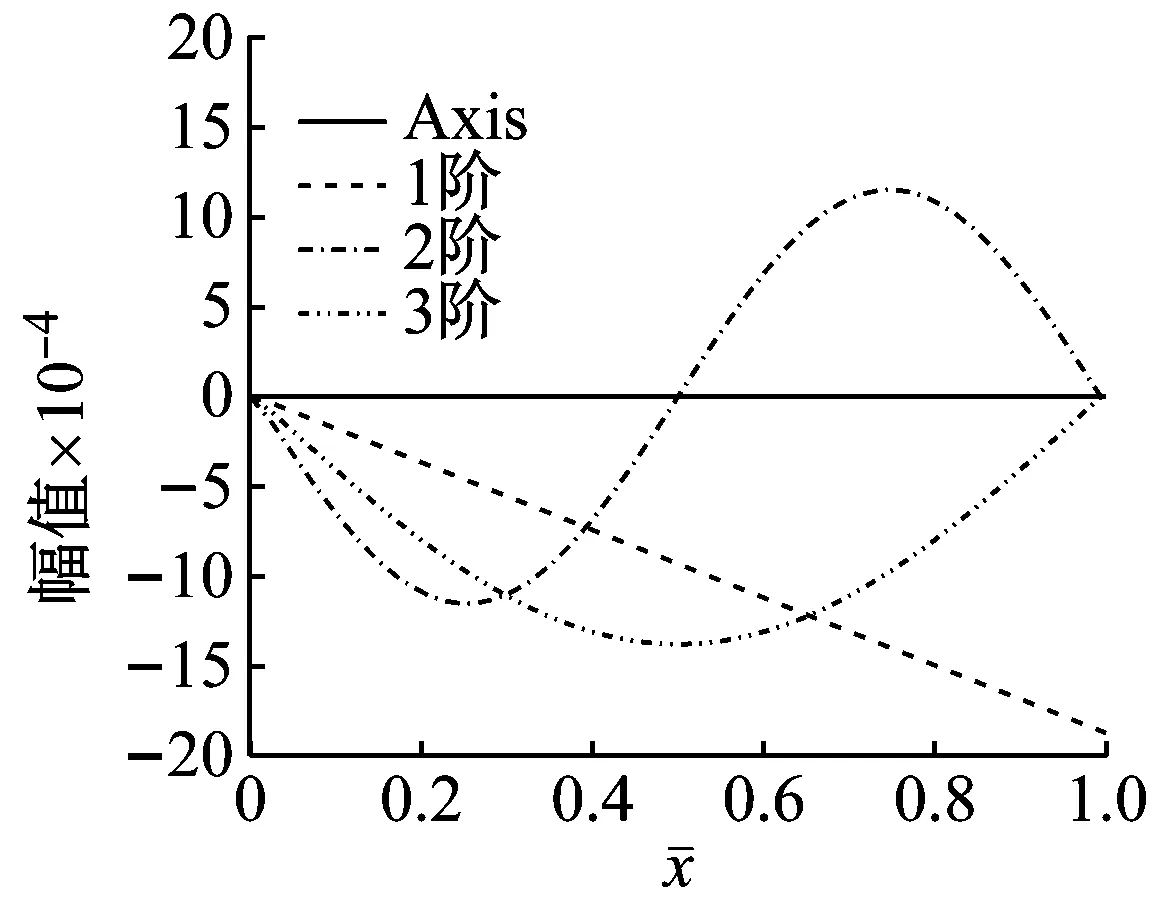
(e) 固支-自由
(3) 六种经典边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁的衰减系数与阶数及约束情况无关,仅与地基土特性及梁自身的尺寸有关,当地基土特性及梁自身的尺寸不发生变化时,黏弹性Pasternak 地基对于Bernoulli-Euler梁振动能量的作用是一个确定的值。
(4) 六种经典边界条件下黏弹性Pasternak 地基上Bernoulli-Euler梁各阶模态曲线的实部与虚部关于轴线对称,其幅值随着阶数的增加而逐渐减小,相邻阶数模态幅值的增量亦随着阶数的增加而逐渐减小。
