圆柱壳体振动主动控制作动器位置优化方法

耿小明, 尹韶平, 周景军, 王 谦

圆柱壳体振动主动控制作动器位置优化方法

耿小明, 尹韶平, 周景军, 王 谦

(中国船舶集团有限公司 第705研究所, 陕西 西安, 710077)

以圆柱壳体为研究对象, 对其振动主动控制中的作动器位置优化问题进行了研究, 采用可控性优化配置准则并对其进行了推导分析, 利用遗传算法完成圆柱壳体内作动器位置的快速寻优。研究结果表明, 优化得到的圆柱壳体内作动器布放位置能获得更佳的振动控制效果, 验证了以圆柱壳体为被控结构的作动器位置优化方法的可行性, 为紧凑空间结构的振动控制及振动传递抑制提供一种作动器布局优化方法。

圆柱壳体; 振动主动控制; 作动器; 位置优化; 遗传算法

0 引言

隐蔽性是水下航行器必备的性能之一, 隐身技术对于水下航行器的生存能力有非常重要的影响[1]。传统的被动控制方法对于低频振动控制效果不理想, 而振动主动控制可以对低频振动进行有效控制。振动主动控制的效果不仅取决于主动控制器的设计, 还取决于作动器作用位置的合理选取, 为了在紧凑空间内利用有限数量的作动器进行振动主动控制, 作动器的位置优化成为关键。作动器的作用位置决定了振动主动控制系统的可控性, 其合理的布放位置可实现对被控结构低频振动的有效控制, 否则会导致系统失稳。

结构振动主动控制的作动器位置优化研究主要从设计优化准则和优化算法2个方面进行[2]。可控性优化准则, 就是要通过优化作动器位置来提高被控模态的可控度。Hamdan等[3]基于响应系数矩阵给出了系统可控度的计算方法, 用以进行作动器的优化配置,。Bruant等[4-5]基于可控可观性准则, 以弹性板为被控结构, 进行了作动器和传感器布局优化。张志谊等[6]根据系统的Gramian矩阵特征值的变化情况, 提出了一种评价可控可观度的方法。Li等[7]考虑控制电压, 定义了一种新的基于系统可控度的优化准则。遗传算法是一种随机搜索类优化算法, 由于其兼具全局最优和快速收敛的特性, 已被广泛应用于振动主动控制作动器/传感器位置优化中[8-12]。

由于成本以及空间限制, 需通过有限数量的作动器对被控结构低阶模态进行控制, 从而达到对结构振动控制的目的。水下航行器动力装置产生的振动通过支撑结构传至壳体, 再通过壳体传递到头段, 会严重影响声呐性能, 因此, 实现对水下航行器壳体上振动及其传递的抑制有重要意义。文中以圆柱壳体为研究对象, 建立一种作动器位置优化方法, 以抑制和衰减壳体上振动的传递, 通过建立其有限元模型, 从结构的动力学方程出发, 基于状态空间方程和可控性准则建立控制性能指标, 利用遗传算法来求解作动器最优的作用位置, 并通过振动主动控制系统仿真和试验验证理论优化结果的合理性。

1 基于遗传算法的作动器位置优化

1.1 优化准则

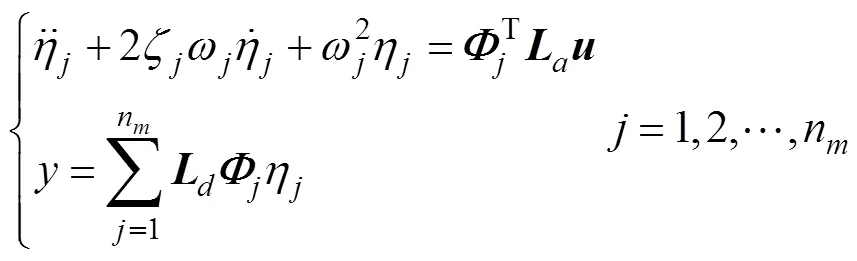
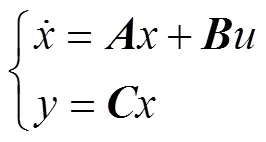
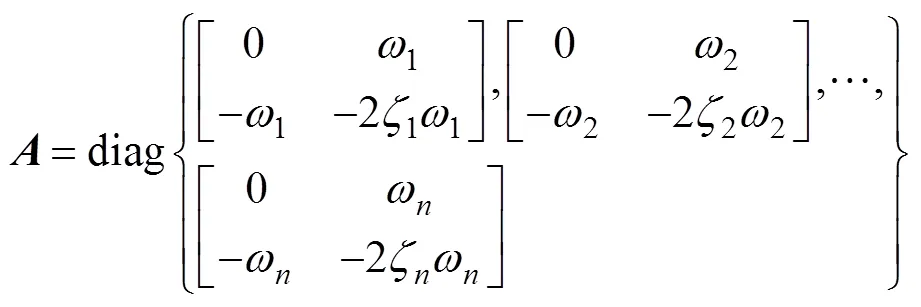
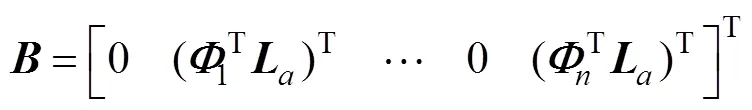
采用可控性优化准则, 利用可控Grammian矩阵来优化作动器布局[15]。为了使作动器的控制能量最小, 可定义优化目标函数为

其中

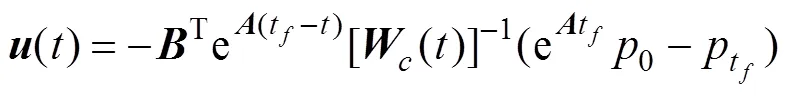
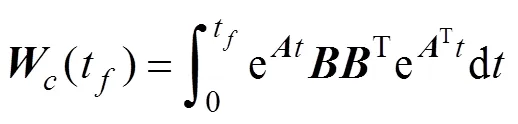
则式(6)可变换为

其李雅普诺夫方程表示为

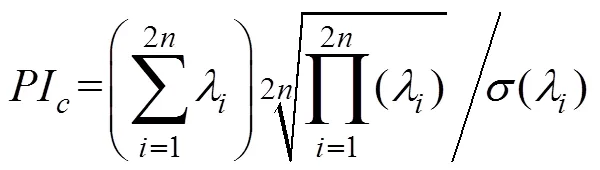
1.2 作动器位置优化遗传算法

遗传算法是借鉴了生物界自然选择和进化机制发展起来的高度并行、随机及自适应的搜索算法[12]。在进行多个作动器位置优化时, 遗传算法能够保证全局最优的优化效果[13], 其操作步骤如下。

1) 编码与解码

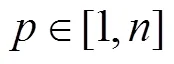
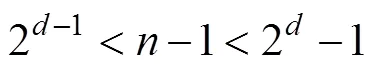
解码过程为从遗传子型到表现型的映射, 即将二进制串到节点编号的映射, 解码公式为

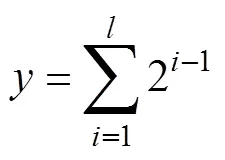
2) 生成初始种群

在上述编码后的解空间内随机生成个初始带有特征的染色体实体, 即二进制串的结构, 将这个带有特征的染色体实体作为优化过程的初始种群。

3) 求解适应度

在遗传算法中, 适应度是用来评价每个个体的优劣程度指标。利用式(11)求解适应度值。

4) 交叉操作

5) 变异操作

6) 选择操作

以适应度值为标准, 从每一代群体中选择优质个体进行保留至下一代参与进化。

2 圆柱壳体作动器位置优化数值算例

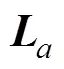
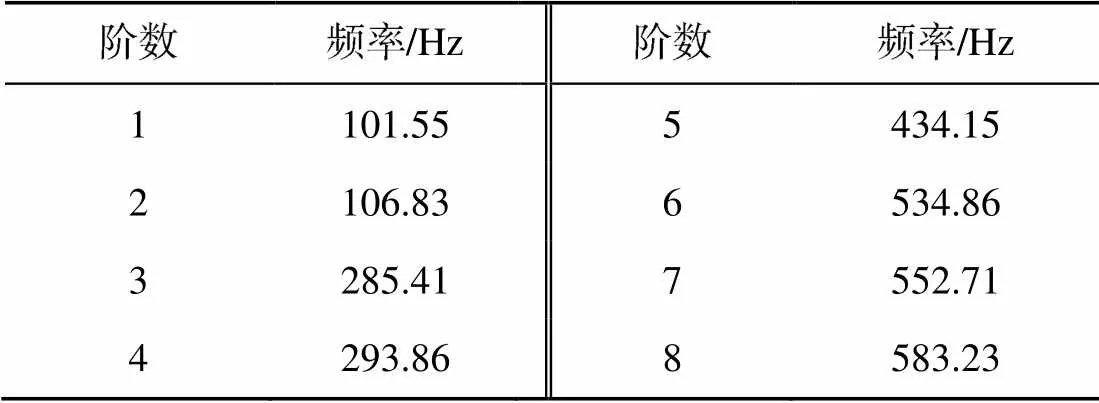
表1 圆柱壳体前8阶模态频率

在圆柱壳体上选若干点作为作动器备选的作用点, 以这些点作为遗传算法优化求解的解空间。圆柱壳体作动器的备选点如图1所示, 图2为圆柱壳体沿节点1~9的母线展开的平面图。

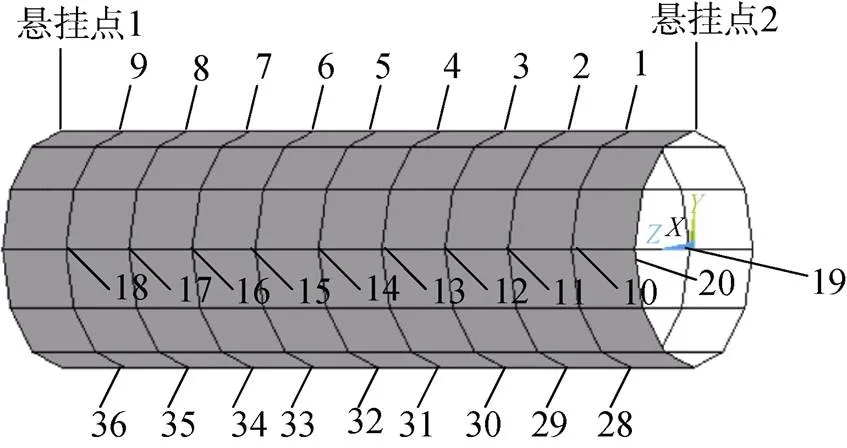
图1 作动器可选布置位置编码

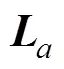
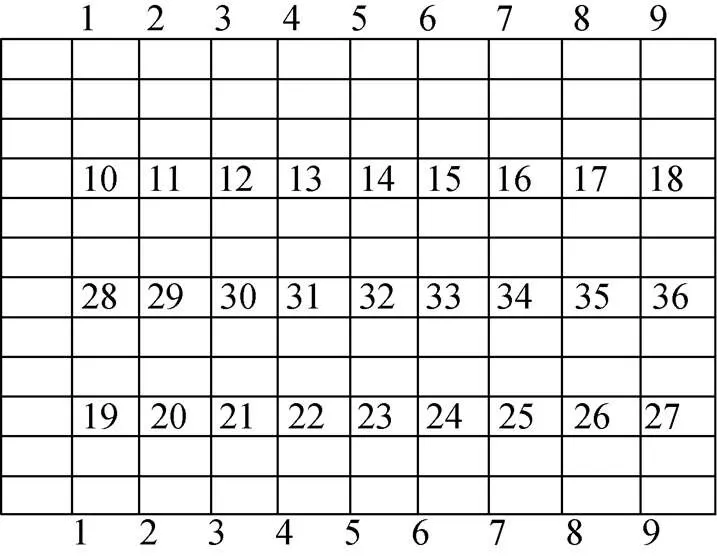
图2 作动器可选位置编码展开图

为了抑制水下航行器动力装置产生的振动向头段传递, 在圆柱壳体模型一端布置激振器模拟动力装置产生的振动, 另一端选一测试点布置传感器, 作为控制的目标点, 在此基础上进行作动器位置寻优。理论上作动器数量越多控制效果越好[13], 但对于紧凑空间的水下航行器, 其内部空间有限, 因此对作动器数量有严格限制, 文中将作动器数量设定为4, 遗传算法优化求解流程如图3所示。

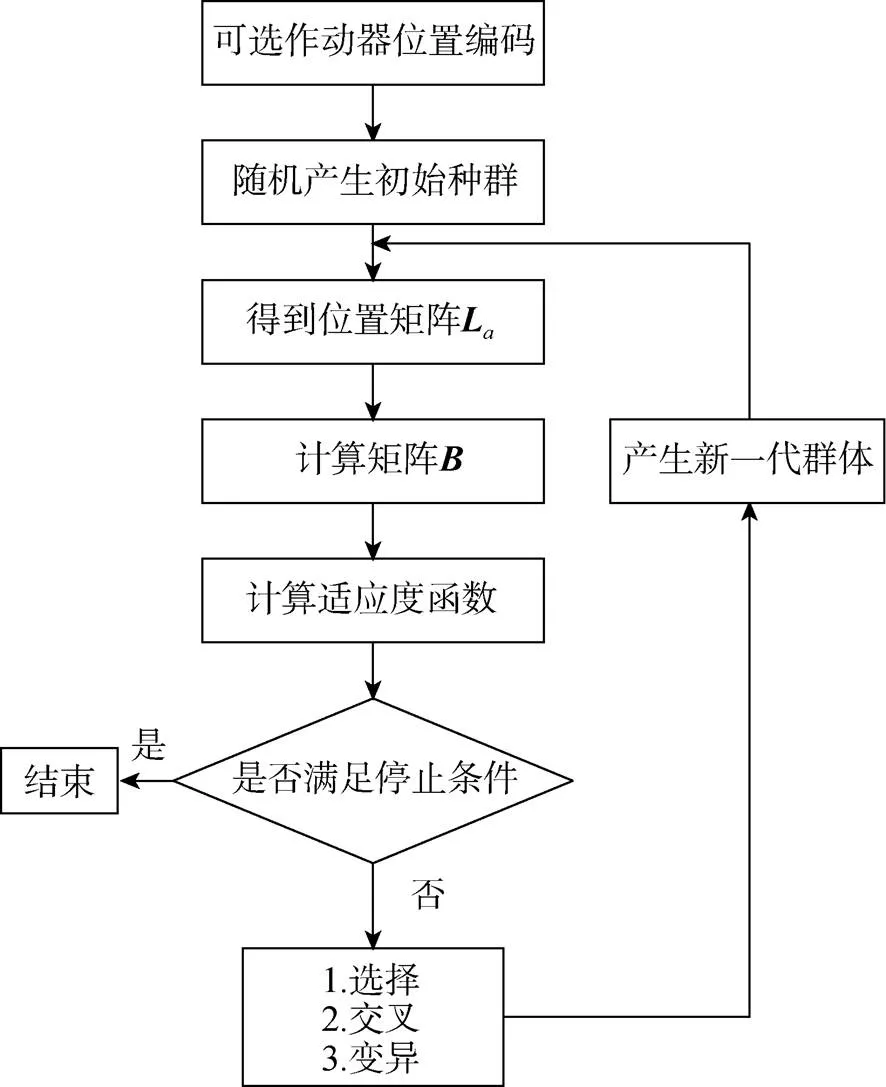
图3 基于遗传算法的作动器位置优化流程图

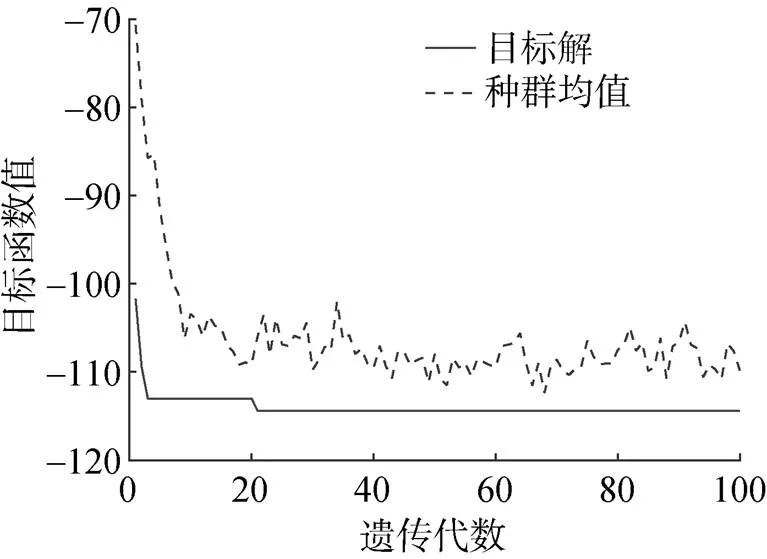
图4 遗传算法进化曲线

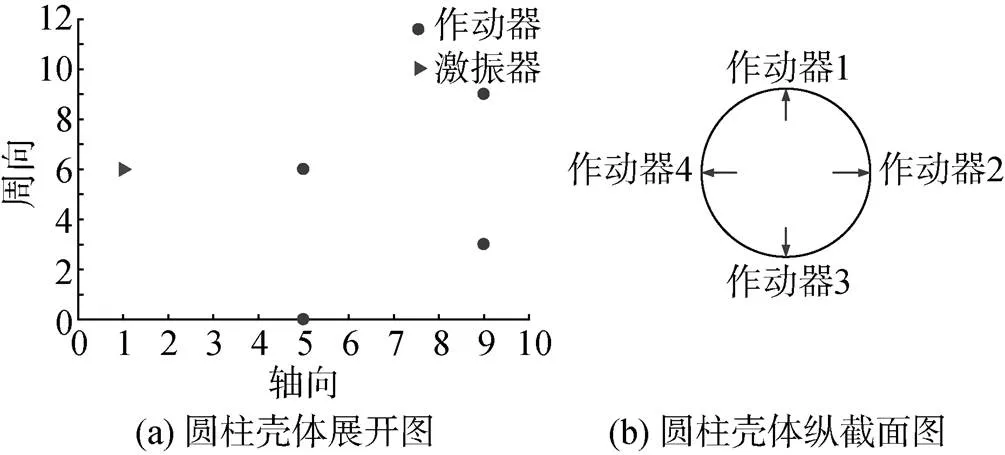
图5 圆柱壳体作动器布置图

3 作动器最优布局仿真和试验验证

3.1 仿真分析

为了验证上述优化的作动器位置对圆柱壳振动的控制效果, 基于MATLAB/simulink搭建振动主动控制仿真模型, 设定3组不同的作动器布置方案, 与优化后的作动器布置方案进行对比分析。

文中的振动主动控制仿真中, 在图1中激振器对应的编号为28的位置输入单频激励信号。

取激励信号为振动主动控制系统的参考信号。在图1中编号为36的位置作为传感器的布置位置, 并作为观测点。由上面的优化结果可知, 作动器的布置位置对应的编号依次为5、18、27、32。

设定激励信号为频率由50~1 000 Hz的11组不同的单频信号, 对作动器理论优化位置的振动控制效果进行仿真分析。其中, 激励频率为50 Hz时未加控制信号和加控制信号时时域和频域的结果对比如图6所示(红色虚线和蓝色实线分别表示未加控制和加控制信号的观测点振动响应)。

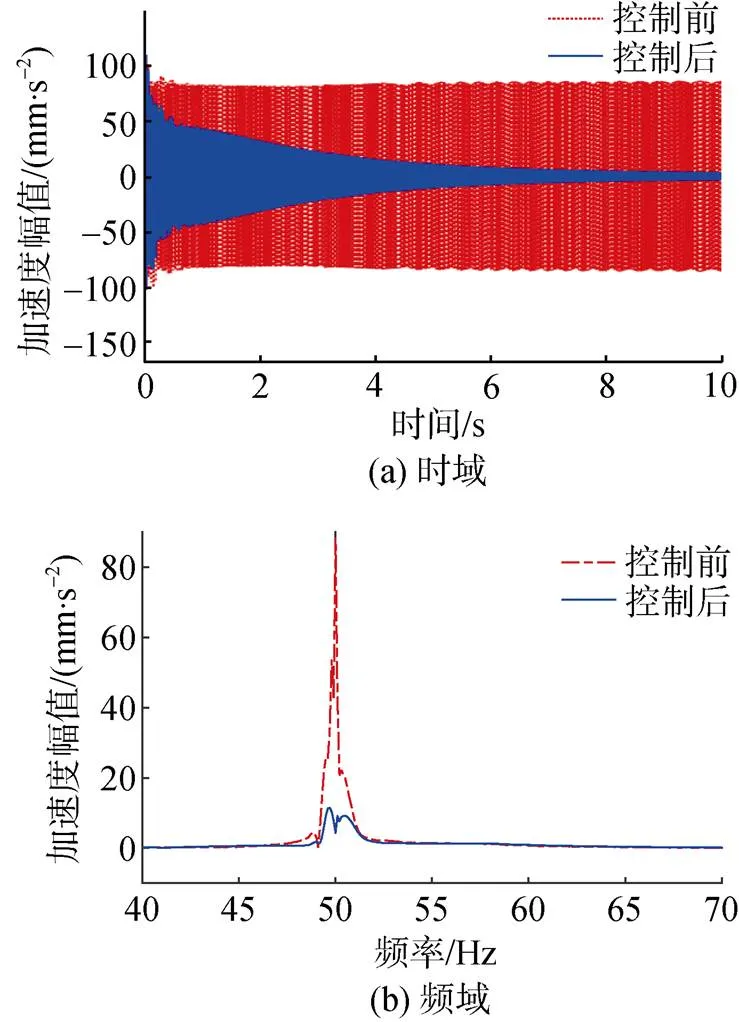
图6 理论优化组控制前后观测点振动响应

不同频率激励信号下理论优化组的控制效果如表2所示, 结果表明, 优化的作动器位置可以有效进行圆柱壳体的振动主动控制, 激励信号小于100 Hz时的振动响应降低量为70%以上, 随着频率升高, 控制效果变差, 由此表明, 振动主动控制对低频信号控制效果较好, 对高频信号控制效果差。

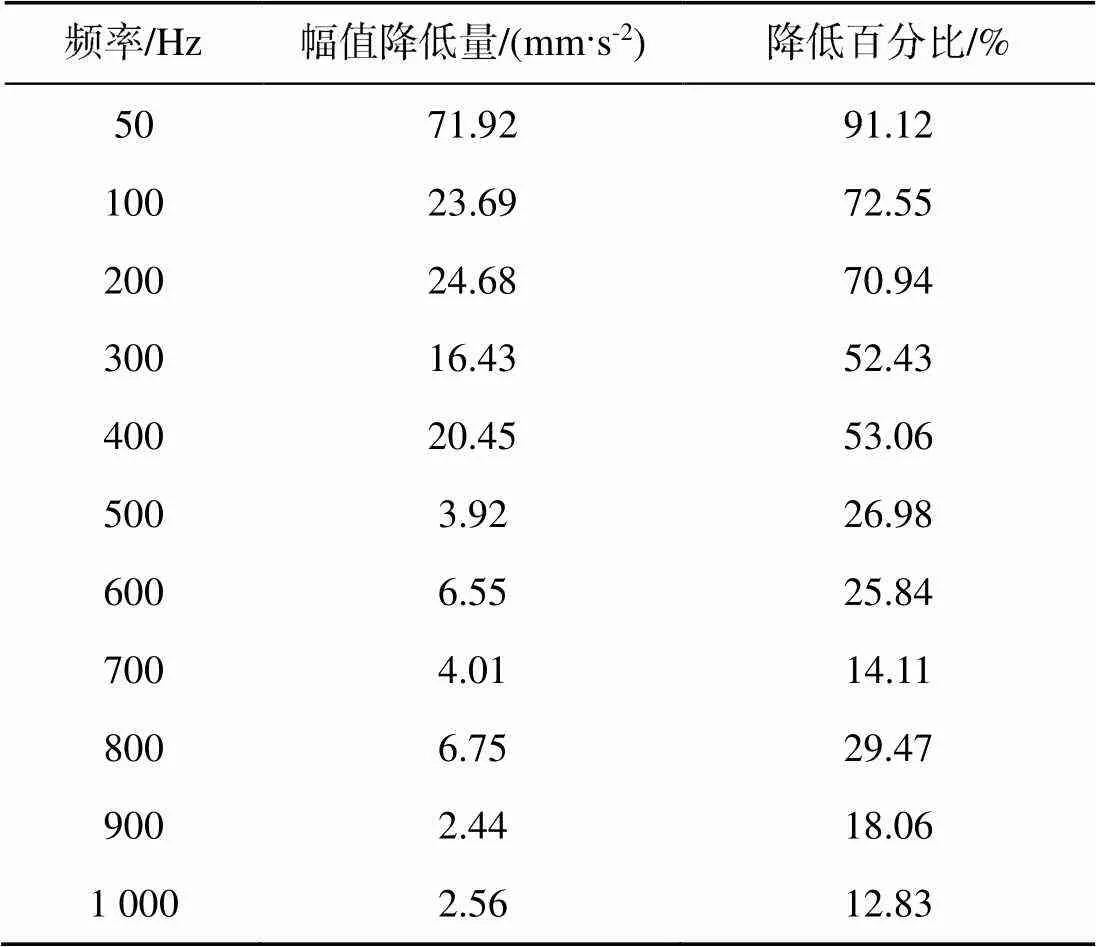
表2 作动器优化位置振动主动控制效果

为了验证理论优化结果的有效性, 随机设定3组布置方案与优化位置结果进行对比。对照组1的作动器布置位置节点编号依次为22、23、24、25, 对照组2的作动器布置位置节点编号依次为2、11、20、29, 对照组3的作动器布置位置节点编号依次为6、14、22、30, 对照组作动器布置如图7所示。通过仿真得到的控制效果对比图如图8所示(激励频率为50 Hz), 不同频率下对照组和优化组控制效果对比如表3所示。

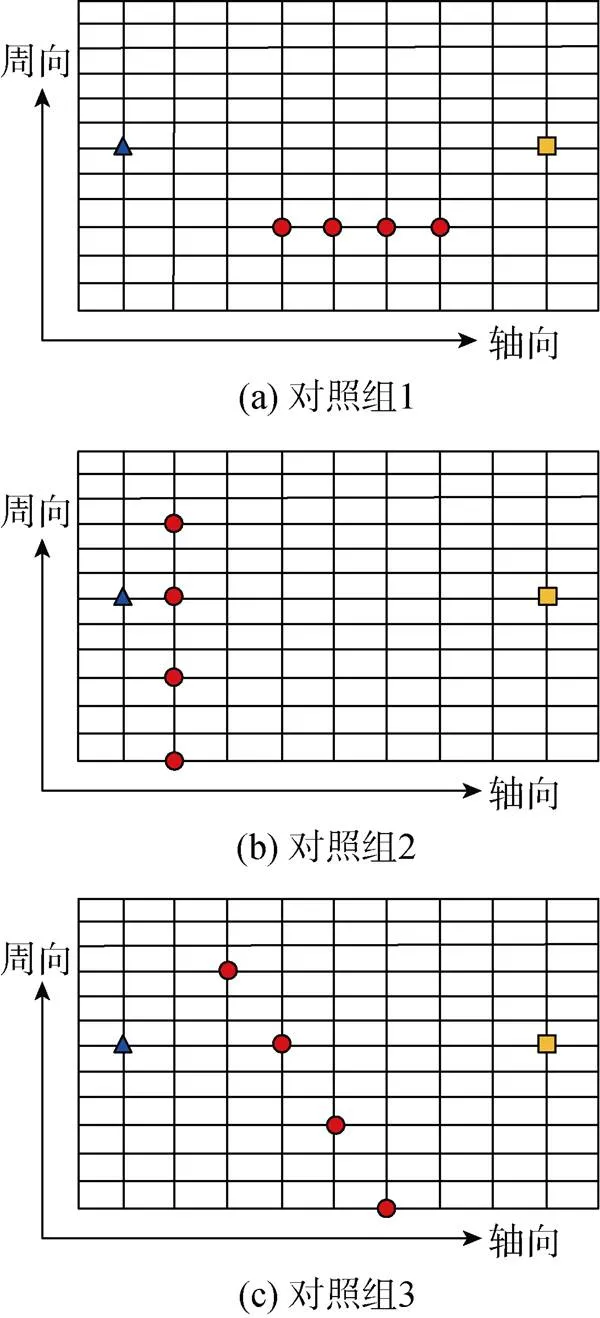
图7 对照组作动器布置图

对仿真结果中观测点的振动信号进行对比可知, 作动器优化位置进行振动主动控制时取得的效果明显优于3个对照组, 不同频率激励下, 理论优化组的控制后观测点振动响应较控制前的降低量高于对照组, 低频激励时优化组和对照组均能进行有效的振动控制, 随着激励频率升高, 各对照组会造成观测点振动响应量级的升高。综合以上仿真结果可知, 除了优化组, 对照组3控制效果最好, 对照组2次之, 对照组1控制效果最差。该仿真对比结果也验证了优化后的作动器位置布局能够更有效地对圆柱壳体的振动进行抑制。同时, 通过振动主动控制仿真也验证了以圆柱壳体为被控结构的作动器优化配置方法的可行性。

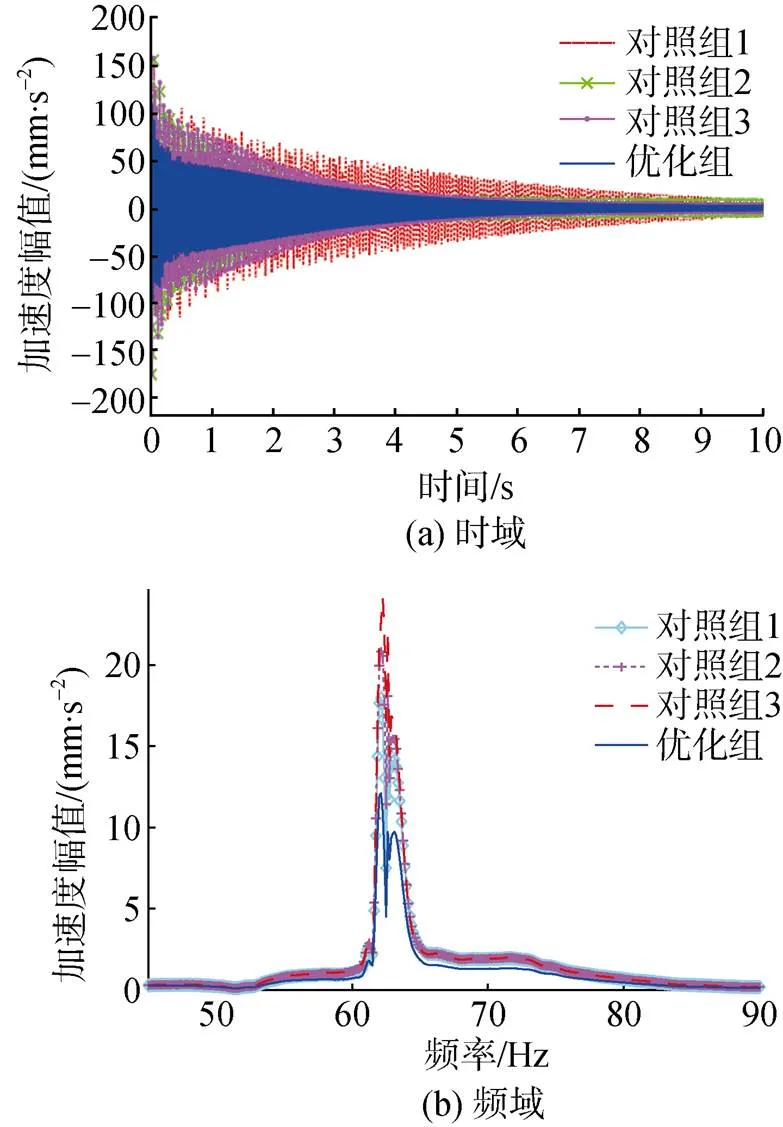
图8 作动器优化位置与对照组控制效果对比图

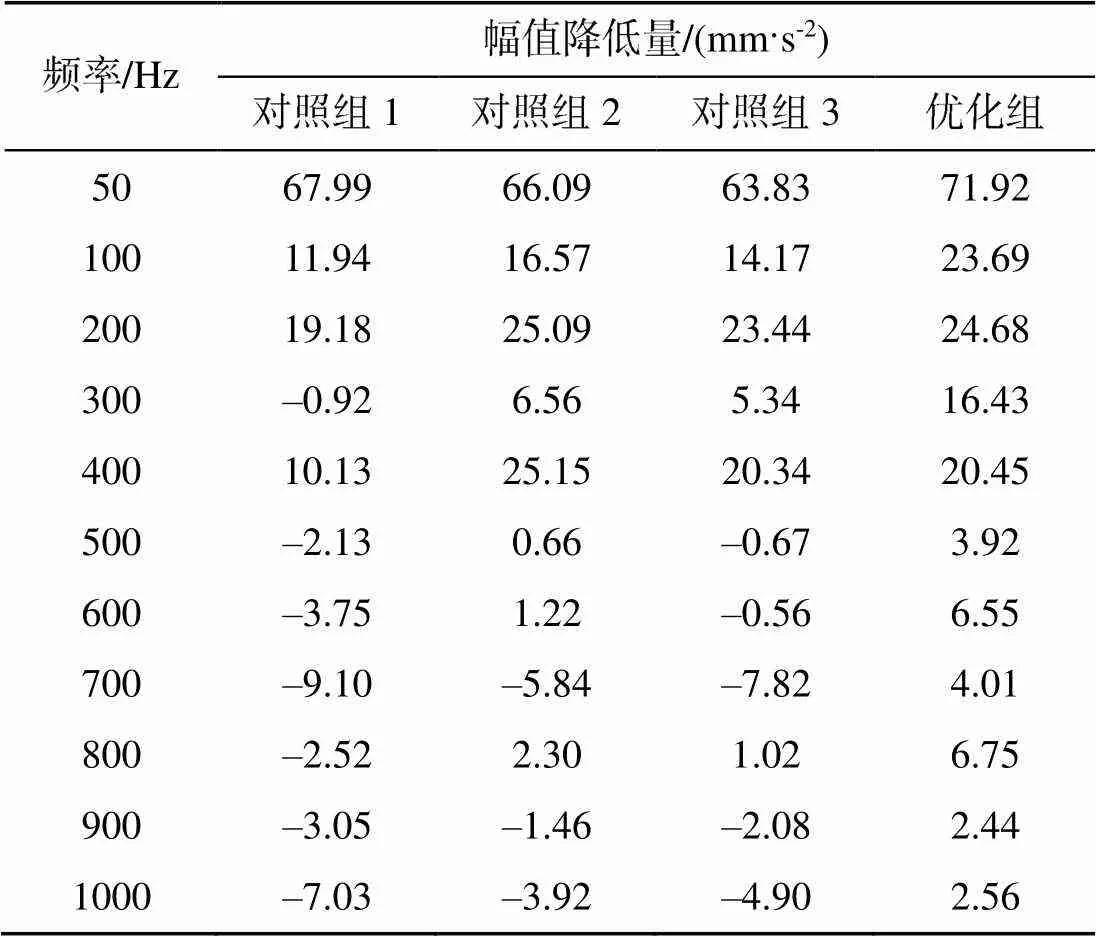
表3 对照组和优化组的振动主动控制效果

3.2 试验分析

振动主动控制试验系统接线图如图9所示,作动器安装图如图10所示。作动器粘贴固定于圆柱壳体的内表面, 输出沿圆柱壳径向的控制力。激振器、作动器和传感器安装位置同上文。试验中利用激振器模拟水下航行器动力装置激励壳体引起的振动初级源, 激励信号经功率放大器后驱动激振器激励圆柱壳体振动, 加速度传感器采集振动信号输入振动主动控制器的模拟/数字(ana- logue to digital, A/D)输入端, 作为参考信号; 利用另一加速度传感器检测壳体端的振动信号并作为误差信号; 振动主动控制器根据输入的参考信号、误差信号, 以FxLMS算法为控制算法进行自动调整自适应滤波器的各权系数得到抵消信号, 该信号通过D/A转换后输入到作动器进行振动控制。

图9 振动主动控制试验系统接线图

图10 作动器安装图

由于篇幅限制, 只列举以50 Hz单频激励信号作为激励力的振动主动控制试验结果。对于激振器产生的50 Hz的单频激振力作用下, 作动器位置优化组和各对照组的观测点振动响应结果如图 11所示。试验结果表明, 优化组的控制效果最好, 观测点振动量级降低了约13 dB; 3个对照组的观测点振动量级分别降低了约7 dB、8.7 dB和10.3 dB。由此表明, 优化的作动器位置对振动传递的抑制更有效, 该试验验证了仿真结果的正确性, 也证明了文中作动器理论优化方法的有效性。

4 结束语

为了抑制水下航行器动力装置产生的振动沿壳体向头段传递, 以圆柱壳一端的观测点的振动量级为控制目标, 对圆柱壳体内的作动器位置进行优化。基于有限元动力学建立振动主动控制系统的数学模型, 基于系统可控性的优化准则, 利用遗传算法对作动器的作用位置进行快速寻优, 最后通过simulink仿真和振动主动控制试验对优化结果进行了验证。结果表明: 利用遗传算法可以有效解决圆柱壳体振动主动控制中作动器的位置优化问题, 完成圆柱壳内作动器布置位置的快速寻优, 更好地进行圆柱壳体的振动及其传递抑制。

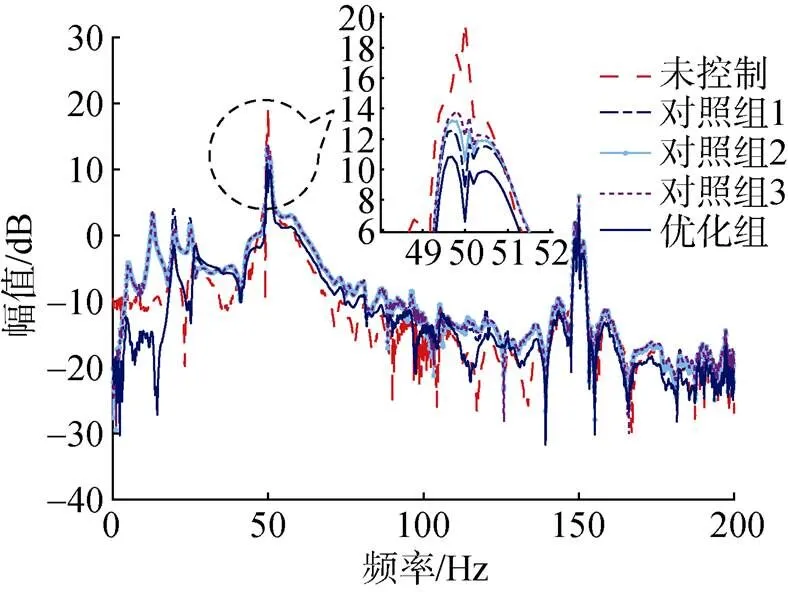
图11 振动主动控制试验结果

[1] 尹韶平. 鱼雷减振降噪技术[M]. 北京: 国防工业出版社, 2016.

[2] 胡泽超, 何琳, 李彦. 圆柱壳体振动主动控制中作动器的优化配置[J]. 船舶力学, 2019, 23(11): 1376-1386.

Hu Ze-chao, He Lin, Li Yan. Optimal Placement of Actuators in Active Control of Cylindrical Shells[J]. Journal of Ship Mechanics, 2019, 23(11): 1376-1386.

[3] Hamdan A M A, Nayfeh A H. Measures of Modal Controllability and Observability for First- and Second-Order Linear Systems[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(3): 421-428.

[4] Bruant I, Gallimard L, Nikoukar S. Optimal Piezoelectric Actuator and Sensor Location for Active Vibration Control, Using Genetic Algorithm[J]. Journal of Sound and Vibration, 2010, 329(10): 1615-1635.

[5] Bruant I, Proslier L. Optimal Location of Actuators and Sensors in Active Vibration Control[J]. Journal of Intelligent Material Systems and Structures, 2016, 16(3): 197-206.

[6] 张志谊, 傅志方, 饶柱石. 模态的可观可控度与作动器、传感器的布置[J]. 振动与冲击, 1998, 17(2): 8-11, 96.

[7] Li D X, Liu W, Jiang J P, et al. Placement Optimization of Actuator and Sensor and Decentralized Adaptive Fuzzy Vibration Control for Large Space Intelligent Truss Structure[J]. Science China(Technological Sciences), 2011, 54(4): 853-861.

[8] Foutsitzi G, Gogos C, Hadjigeorgiou E, et al. Actuator Location and Voltages Optimization for Shape Control of Smart Beams Using Genetic Algorithms[J]. Actuators, 2013, 2(4): 111-128.

[9] Hale J M, Daraji A H. Optimal Placement of Sensors and Actuators for Active Vibration Reduction of a Flexible Structure Using a Genetic Algorithm Based on Modified Hinfinity[J]. Journal of Physics: Conference Series, 2012, 382: 012036.

[10] Li D S, Cheng L, Gosselin C M. Optimal Design of PZT Actuators in Active Structural Acoustic Control of a Cylindrical Shell with a Floor Partition[J]. Journal of Sound and Vibration, 2004, 269(3-5): 569-588.

[11] Jia S, Jia Y, Xu S, et al. Optimal Placement of Sensors and Actuators for Gyroelastic Body Using Genetic Algorithms[J]. AIAA Journal, 2016, 54(8): 2472-2488.

[12] 郭延宁, 王鹏宇, 金珊. 一种新型的挠性航天器作动器布局优化方案[J]. 飞控与探测, 2019, 2(5): 49-54.Guo Yan-ning, Wang Peng-yu, Jin Shan. A New Optimization Approach to the Flexible Spacecraft Actuators Placement[J]. Flight Control & Detection, 2019, 2(5): 49-54.

[13] 高维金, 王亮, 刘永光. 作动器最优配置的柔性结构振动主动控制[J]. 国防科技大学学报, 2018, 40(1): 161- 167.

Gao Wei-jin, Wang Liang, Liu Yong-guang. Active Vibration Control with Optimal Actuator for Flexible Structures[J]. Journal of National University of Defense Technology, 2018, 40(1): 161-167.

[14] HAĆ A, Liu L. Sensor And Actuator Location In Motion Control of Flexible Structures[J]. Journal of Sound and Vibration, 1993, 167(2): 239-261.

[15] Sohn J W, Choi S B, Kim H S. Vibration Control of Smart Hull Structure with Optimally Placed Piezoelectric Composite Actuators[J]. International Journal of Mechanical Sciences, 2011, 53(8): 647-659.

Position Optimization Method for an Active Vibration Control Actuator of a Cylindrical Shell

GENGXiao-ming, YIN Shao-ping, ZHOU Jing-jun, WANG Qian

(The 705 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 710077, China)

In this study, with a cylindrical shell used as a research object, the actuator position optimization problem in the active vibration control of the cylindrical shell is studied. A controllability optimization configuration criterion is employed, a derivation analysis is conducted, and the cylinder is constructed using a genetic algorithm to quickly identify the position of the actuator in the shell. Results show that this method for optimizing the position of the actuator with the cylindrical shell as the control structure can improve the vibration control effect. The method can thus be applied for use in vibration control and vibration transmission suppression in a compact space structure.

cylindrical shell; active vibration control; actuator; position optimization; genetic algorithm

TJ630.31; TB53

A

2096-3920(2020)06-0650-07

10.11993/j.issn.2096-3920.2020.06.009

2020-07-23;

2020-09-25.

海军武器装备预先研究背景项目资助(1020901010103).

耿小明(1995-), 男, 在读硕士, 主要研究方向为无人水下航行器总体技术.

耿小明, 尹韶平, 周景军, 等. 圆柱壳体振动主动控制作动器位置优化方法[J]. 水下无人系统学报, 2020, 28(6): 650-656.

(责任编辑: 许 妍)