基于作战环境配置资源的出动架次率计算模型

彭雅欣, 黄 琦, 余明晖, 杨 杰, 苏厚胜

基于作战环境配置资源的出动架次率计算模型

彭雅欣1, 黄 琦2, 余明晖1, 杨 杰1, 苏厚胜1

(1. 华中科技大学 人工智能与自动化学院, 湖北 武汉, 430074; 2. 中国舰船研究设计中心, 湖北 武汉, 430064)

舰载机、无人艇等海军武器的出动架次率(SGR)是判断其综合作战能力的关键指标, 作战环境的资源配置将影响SGR, 因此研究作战环境的配置资源最优组合将有利于提高系统的作战能力。文中以航母舰载机为例, 在对波次出动模型进行研究的基础上, 建立仿真SGR计算模型, 针对其需重复计算以降低计算结果随机性的问题, 利用反向传播(BP)神经网络对仿真模型进行拟合, 得到BP-SGR计算模型, 并使用该模型进行甲板资源配置优化研究。仿真实验表明, BP-SGR计算模型得到的21组最优资源配置组合SGR值, 均落在仿真模型SGR计算结果99%预测区间内, 且二者相对误差均小于1%, 验证了该模型在资源配置优化问题的适用性。使用该模型可有效对舰载机、无人艇等作战资源配置问题进行求解。

海军武器; 出动架次率; 资源配置; 波次出动; 反向传播神经网络

0 引言

航空母舰有着极强的海空攻防作战能力, 舰载机作为航母的核心作战装备, 是其主要的作战力量, 对航母的综合作战能力有很大影响[1]; 无人艇(unmanned surface vessel, USV)作为海面作战的重要装备, 可进行海洋环境监测、反潜战、可疑目标打击和特种作战等多种作战任务[2]。在执行作战任务时, 舰载机、无人艇在有限资源内的出动能力, 即出动架次率(sortie generation rate, SGR)是衡量系统作战能力的关键指标。对于SGR的计算, Stillion等[3]提出一种单架舰载机的SGR计算模型; Harris等[4]将维修任务考虑为分叉节点, 建立了排队网络模型, 提出了基于平均值分析法的舰载机SGR计算解析模型; 夏国清等[5]将调运中心看作共享资源, 建立了闭排队网络, 使用平均值分析法计算SGR; 郑茂等[6]利用基于蒙特卡洛的仿真对舰载机高峰SGR进行计算; 陈成[7]运用离散时间和基于智能体的混合建模方法, 建立了舰载机出动回收仿真模型, 对SGR进行计算。

上述计算模型主要分为基于排队网络的解析计算模型和仿真计算模型, 前者无法考虑舰载机波次出动模式, 而后者计算时间长, 成本高, 不利于研究多种资源配置组合下的SGR。为此, 文中提出一种用于研究资源配置对SGR影响的计算模型, 可快速计算舰载机、USV等作战武器在波次出动作业中不同资源下的SGR。为求解该模型, 以航母舰载机为例, 首先建立舰载机波次出动的仿真模型, 后利用反向传播(back propagation, BP)神经网络对该仿真模型进行拟合, 并验证其效果, 得到可在波次出动模式下快速计算SGR的计算模型; 最后基于该模型研究各种配置参数对SGR的影响, 寻找最优的资源配置组合。

1 波次出动模型建立

1.1 波次出动流程

舰载机的出动回收是指舰载机以完成作战任务为目的, 从航母飞行甲板上起飞、降落及保障的过程[8]。航母飞行作业分为连续作业模式和波次作业模式[9]2种, 连续性作业模式适合于防御型任务安排的情况, 而执行攻击型作战任务多采用波次作业模式, 文中主要研究作战任务下的SGR, 因此将考虑波次作业模式。

舰载机与无人艇均属于常见的作战武器, 无人艇作战多以集群形式出动, 协同合作作战, 二者在出动回收过程中的共同点在于:

1) 一组协同编队无人艇的出动规模与一个波次舰载机的规模相近;

2) 一组无人艇将一同出动、执行任务并回收, 与舰载机波次出动方式类似;

3) USV和舰载机在执行作战任务时, 均需从指定区域以规定的顺序和方式出动, 其出动效果与作战环境的资源配置情况息息相关。

因此, 文中以舰载机波次出动为例, 建立针对作战环境资源对出动效果的研究方法和模型,且同样适用于USV。

舰载机、USV等作战装备进行作战任务时, 会涉及到多种类型, 文中参照美国海军1997年高峰演习[10], 考虑战斗机和预警机2种舰载机, 其中预警机的甲板作业周期假设为当前攻击机甲板周期的倍数, 且尽量接近4 h, 实际时长取决于当前攻击机的作业周期。一般舰载机的出动回收作业将持续12~18 h, 最长可达24 h[11], 文中假设为12 h。

波次作业条件下[6], 航母飞行甲板的作业以甲板作业周期为工作节奏, 它指的是同一种甲板作业2次之间所间隔的时间, 每个甲板作业周期会回收一批舰载机并出动一批舰载机。甲板作业周期有1+00(1 h), 1+15(1 h15 min), 1+30(1 h30 min), 1+45(1 h45 min), 2+00(2 h)等多种。周期类型分为单周期、双周期和三周期, 文中考虑单周期作业: 一个波次的舰载机会在当前周期内起飞, 在相邻的下一个周期内回收, 具体如图1所示。

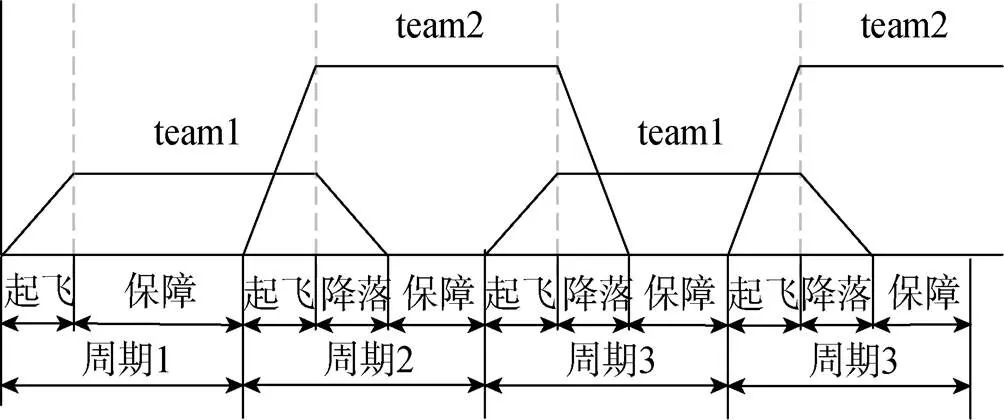
图1 单周期波次出动

一个周期内包含3个事件: 本周期舰载机起飞、上一周期起飞的舰载机回收、下一个周期拟出动舰载机保障。此时舰载机分为2队(team), 其作业情况为; 在周期1中, team1起飞, team2保障; 在周期2中, team2出动, team1回收, 随后team1保障; 在周期3中, team1出动, team2回收, 随后team2保障, 以此周期循环直至任务结束。

1.2 SGR计算参数

影响舰载机SGR的因素很多, 大体上可以分为资源、任务和环境3部分[12]。文中主要考虑资源对舰载机出动架次的影响, 包含甲板作业时间、保障设备弹射器、飞行员和舰载机起降指挥系统等, 这些资源将影响舰载机出动流程中的各种参数。

1) 一站式保障站位数量

传统集中式保障站位是根据不同的功能进行区域划分, 并在不同站位完成不同保障作业, 因此舰载机通常需要在这些区域内频繁来回调度, 才能最终完成起飞和回收作业[13]。而一站式保障站位能够完成舰载机维修、加油及挂弹等所有保障作业, 可大幅度增加保障作业的效率[14], 因此一站式保障站位的数量将影响舰载机的SGR。

2) 平均起飞时间间隔

弹射起飞为航母舰载机起飞的主要方式, 弹射器的数量、维护周期及故障情况将直接影响舰载机的出动速度[12], 文中将利用平均起飞时间间隔代表相关资源的影响情况, 表示同一波次的舰载机起飞时, 相邻两架舰载机的平均时间间隔。

3) 平均降落时间间隔

舰载机降落过程中, 阻拦索、停机区舰载机数量等资源配置条件, 将影响舰载机的降落速率, 文中将利用平均降落时间间隔这一参数体现相关资源的影响, 其表示同一波次的舰载机降落时, 相邻2架舰载机的平均时间间隔。

4) 复飞率

舰载机的降落过程中, 飞行员对舰载机的操作及甲板的降落指挥系统会影响舰载机降落成功率, 舰载机若未成功降落, 则需复飞后再次降落, 文中用复飞率描述该资源的影响, 其表示舰载机降落时, 降落失败需要复飞重新降落的概率。

5) 舰载机完好率

舰载机在保障开始前, 需进行故障诊断, 无故障的舰载机方可进行保障。舰载机完好率指保障的同一波次的舰载机中, 处于完好状态可用于保障起飞的舰载机数量占比, 处于非完好状态的舰载机无法在本波次保障起飞。

6) 甲板作业周期

甲板作业周期为同一种甲板作业2次之间所间隔的时间, 文中考虑的甲板作业周期为2次起飞作业之间所间隔的时间, 同时考虑单周期作业形式, 一个周期内起飞一个波次的飞机, 此时甲板作业周期决定了每波次舰载机的起飞时刻。

2 SGR仿真计算模型

针对上节所述的舰载机波次出动流程进行仿真, 考虑上述参数并计算SGR, 仿真流程如图2所示。仿真时长即为出动回收作业时长, 按前文所述取12 h, 循环部分包含起飞、降落和保障3个部分。针对USV系统, 可根据任务情况选择具体参数, 并自由调整仿真时长。

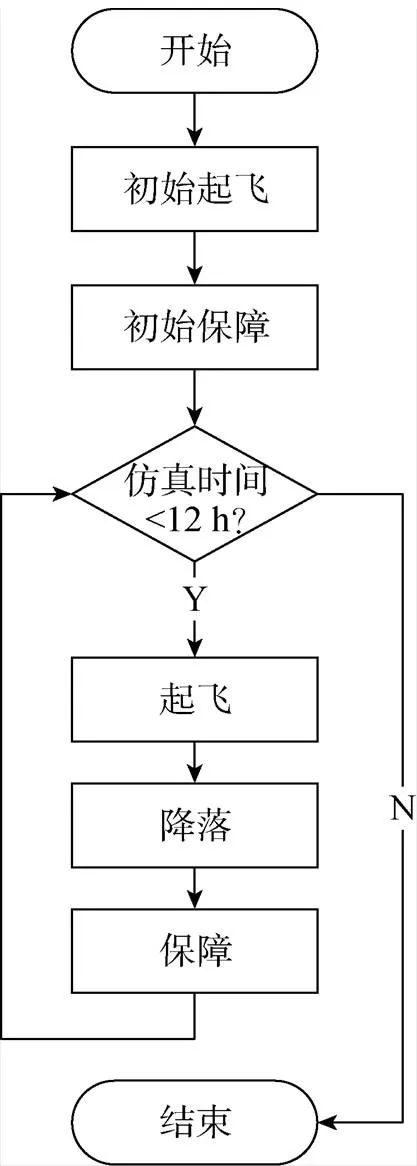
图2 SGR仿真计算模型流程图

2.1 仿真程序设计

仿真流程如图3所示, 仿真以起飞作业开始, 一个甲板作业周期出动一个波次的舰载机, 周期内将完成一个波次飞机的起飞、上个波次飞机的降落及降落飞机的保障。

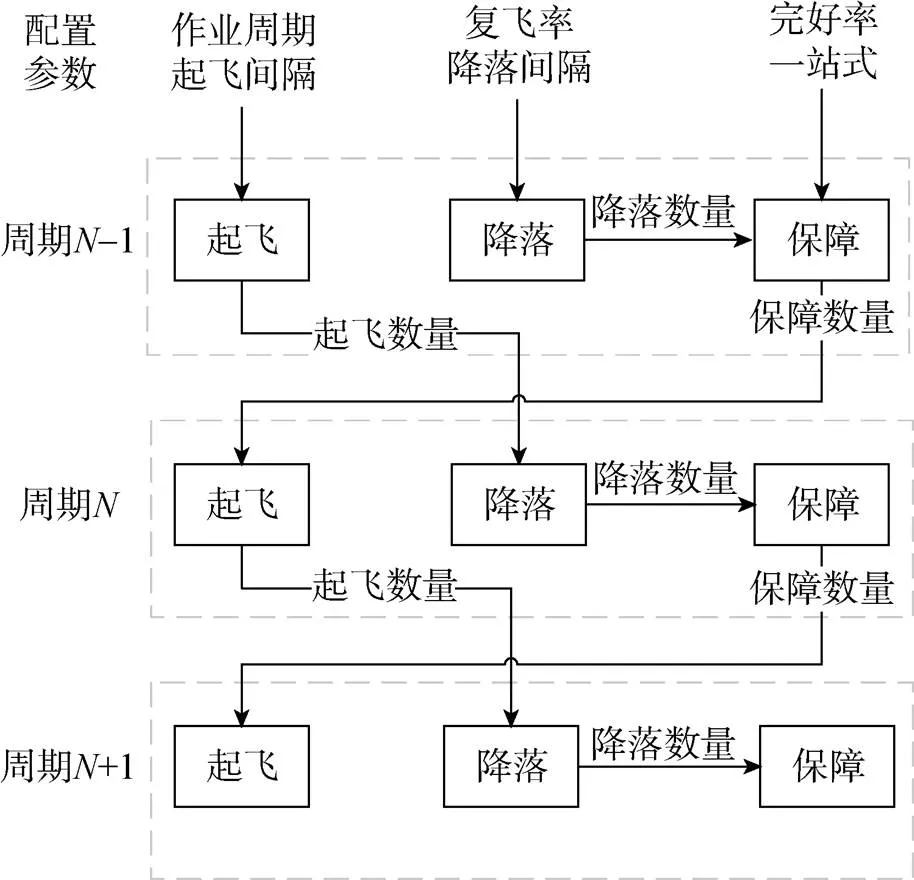
图3 仿真流程示意图

2.1.1 起飞

甲板作业周期和平均起飞时间间隔将对起飞作业产生关键影响, 具体如下

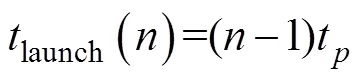
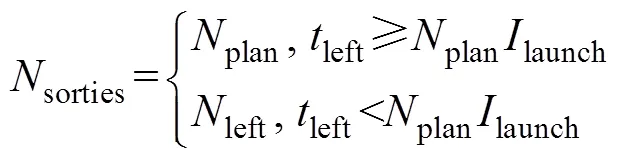
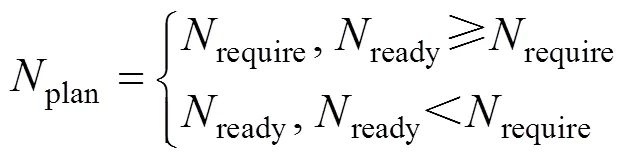
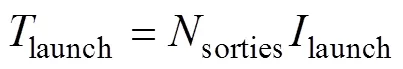
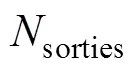
2.1.2 降落

复飞率和平均降落时间间隔将对降落作业产生关键影响。

在舰载机降落过程中, 舰载机复飞将使得实际降落的次数和总降落时长增加。文中考虑对每一架要降落的舰载机, 均需判断其是否需要复飞, 每有一架舰载机需要复飞, 则认为总降落次数增加一次, 因此有

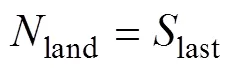
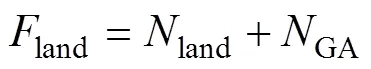
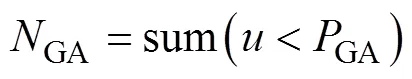
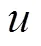
2.1.3 保障

完好率和一站式保障数量将对保障作业产生关键影响。如前所述, 仅完好的舰载机可进行保障作业, 且1个甲板作业周期内, 可用于保障的时长为本周期内完成起飞和降落后的剩余时长, 可完成保障的舰载机数量与当前甲板一站式保障站位数量相关, 因此保障过程有

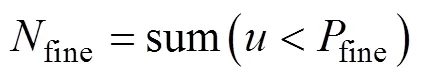
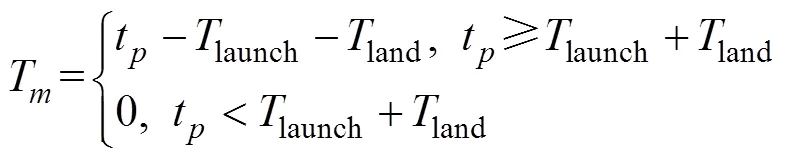
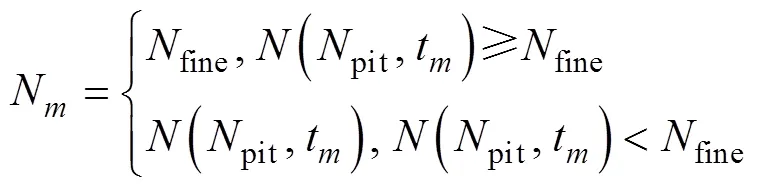
式中:fine为可保障的舰载机数量;fine为完好率;T为可用于保障的时长;(pit,t)为当一站式数量为pit, 可用于保障的时长为t时, 可完成保障的舰载机数量。

2.2 仿真参数设置

仿真参数有一站式保障站位数量、平均起飞时间间隔、作业周期、降落间隔时间、复飞率和舰载机完好率等6种。

美国福特级航母引入了18个一站式保障站位[15], 因此文中也将控制在该范围内; 其余参数设定参照美国海军1997年高峰演习数据[10], 具体配置参数如表1所示。

3 BP-SGR预测模型

SGR计算模型对于研究资源配置优化和瓶颈资源有着重要意义, 文中将基于前文所述的仿真SGR计算模型, 建立BP-SGR预测模型, 并将该模型作为研究航母甲板配置资源的SGR计算模型。

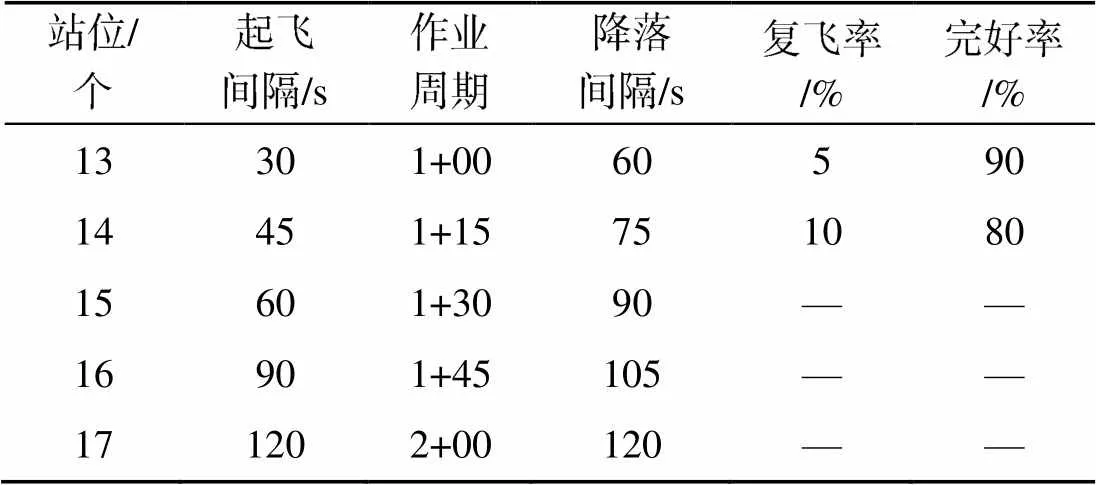
表1 资源配置参数表

3.1 BP-SGR预测模型建立

人工神经网络是人工智能领域一个重要研究方向, 其通过模拟人脑神经元的结构, 刻画隐藏在数据中的非线性关系[16], 其中的BP神经网络[17]特点在于可以实现一个从输入到输出的映射, 具有较强的非线性映射能力, 特别适合于求解内部机制复杂的问题, 与文中研究背景高度契合。

文中所选BP神经网络模型为3层网络拓扑结构。考虑上文6种配置参数, 即6个自变量, 输入层神经元个数为6; 输出为SGR, 即1个因变量, 输出层神经元个数为1; 根据误差精度和训练效果, 最终选择的隐含层神经元个数为25, 图4为BP神经网络结构示意图。

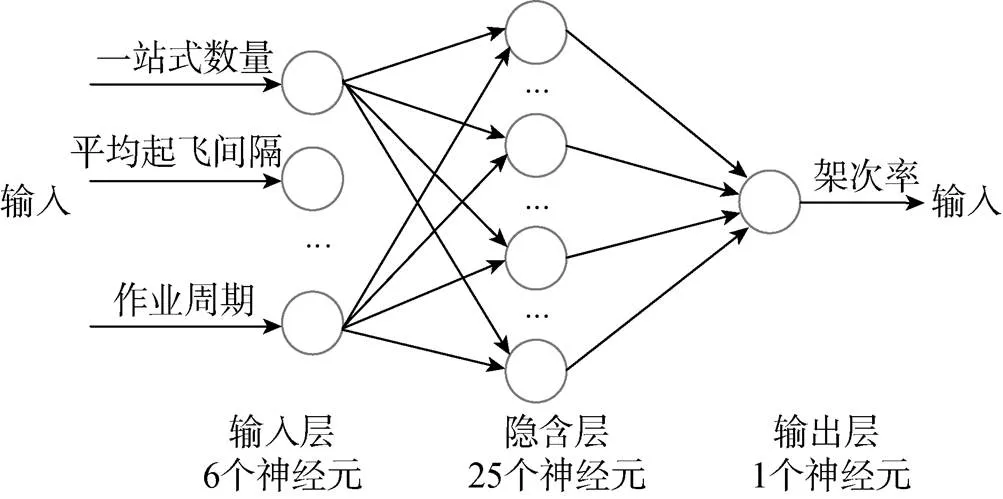
图4 BP神经网络结构示意图

BP神经网络所使用的传递函数均采用如式(12)所示的双曲线正切S型变换函数; 训练算法采用 Levenberg-Marquardt; 性能函数选用均方误差(mean-square error, MSE), 则

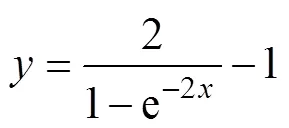
式中:为输出值;为使用该传递函数的输入值。

3.2 训练样本

BP神经网络训练样本来自于第2章所述的仿真计算模型。首先从6种资源参数构成的配置组合中, 随机选取500组; 而仿真计算模型具备随机性, 对同一配置组合, 需重复计算以获取更准确的计算结果, 为保证计算结果可信度, 需确认重复计算的次数, 文中随机选取了100组配置组合, 对其重复计算了500次, 并绘制了仿真样本均值随计算次数变化的曲线图, 如图5所示。

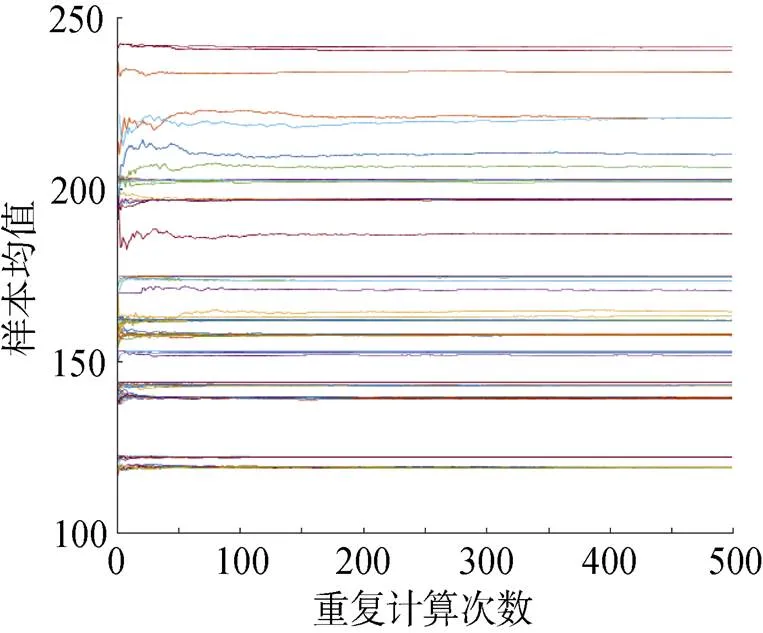
图5 样本均值随仿真次数变化曲线

从曲线变化趋势可知, 当重复计算次数大于100时, 大部分组合的仿真均值已开始收敛, 部分数据仍有小范围浮动, 当重复次数到达500时, 所有组合样本均值已趋于一致, 因此设定500个组合的重复计算次数为500, 可充分保证训练模型计算结果的准确性。

训练过程中75%的数据用于训练, 15%的数据用于交叉验证, 15%的数据用于测试。

3.3 预测模型验证准则

为验证BP-SGR预测模型的准确性, 采用预测区间理论作为验证准则。

参数估计是用样本统计量去估计总体的参数, 其中包含对总体均值和总体方差等的估计[18], 而除此之外, 也希望通过已有样本预测新的观测值, 预测结果无法保证与实际值的完全一致, 但要求其在合理范围之内, 该范围即为预测区间。

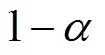
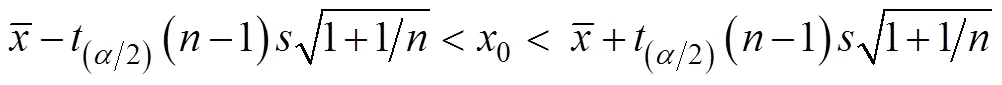
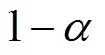
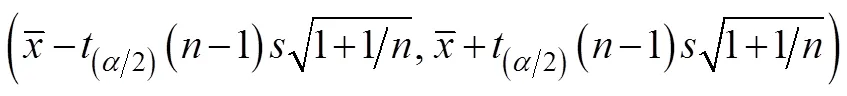
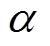
3.4 拟合效果验证

基于上述内容, 随机取训练样本外的50组配置参数, 并针对每组配置参数做如下验证:

1) 利用仿真模型计算100次, 获取100组仿真结果, 计算其均值和标准差, 并利用式(14)计算其99%的预测区间;

2) 利用BP神经网络模型计算SGR;

3) 计算仿真结果均值与BP神经网络模型预测值的相对误差。

对比预测区间和预测值, 结果如表2所示。

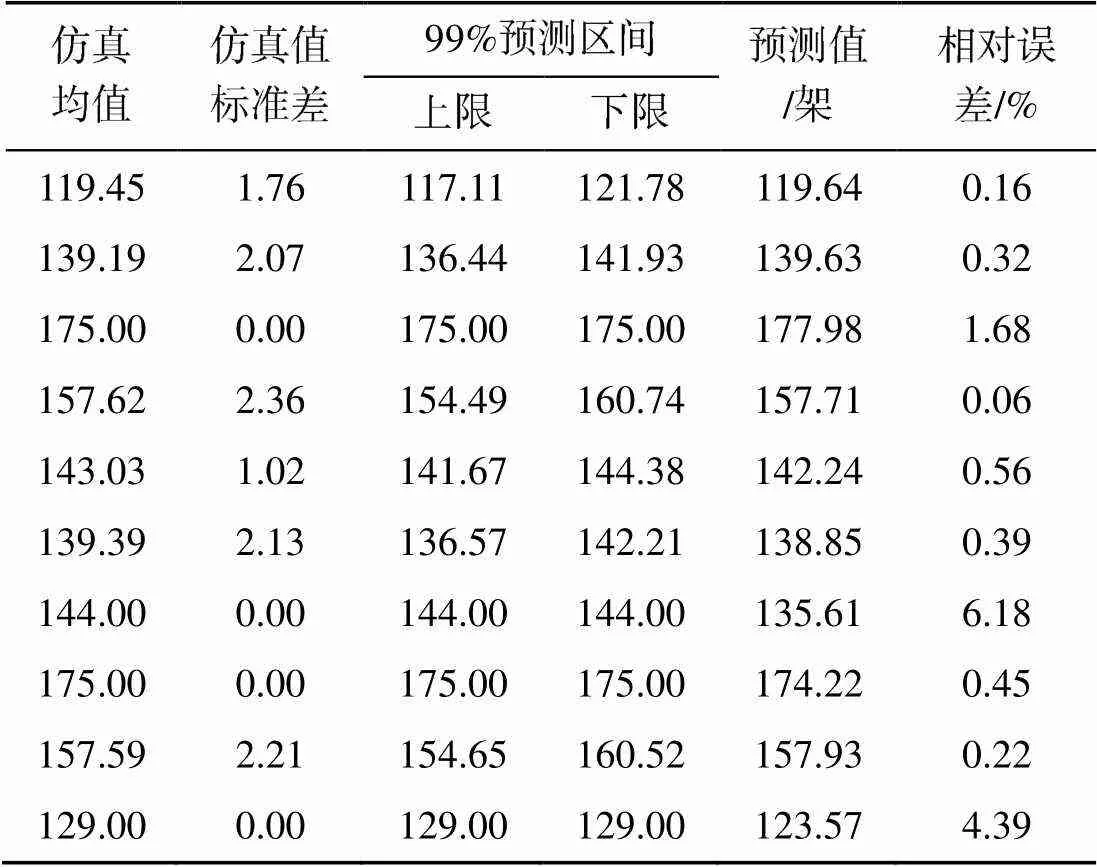
表2 部分验证数据结果

1) 50组实验组合中, 45组实验组合的预测值落入仿真值99%的预测区间内。对于未落在区间的预测值, 其中4组的仿真结果标准差为0, 预测区间宽度为0, 该类数据出现的原因在于, SGR计算结果的随机性来自完好率和复飞率, 而在某些参数组合下, 会出现波次备用机数量足够大或波次剩余保障时长小于0的情况, 此时完好率和复飞率将不会对SGR产生影响, 从而导致SGR计算标准差为0。因此该类数据不宜采用预测区间作为验证指标, 后续将仿真均值和预测结果的相对误差做进一步验证。综合而言, 用预测区间作为验证指标时, 46组数据中, 有45组数据均落入仿真值99%的预测区间内。

2) 以仿真均值和预测结果的相对误差作为验证指标时, 50组实验中, 相对误差最大为6.18%, 其中有42组数据相对误差小于1%, 7组数据相对误差介于1%~5%之间, 1组数据大于5%; 50组数据的平均相对误差为0.73%, 4组标准差为0的数据平均相对误差为3.17%。

综上, 文中构建的BP-SGR预测模型很好地反映了原仿真模型的行为, 其预测结果可作为SGR计算结果, 因此该模型可作为研究航母配置资源的SGR计算模型。相对于仿真SGR计算模型, BP-SGR预测模型的优势在于:

1) 对于某一给定配置组合, 仿真SGR计算模型需多次重复计算以降低结果随机性, 而BP-SGR预测模型仅需计算一次;

2) BP-SGR预测模型的简洁性将有利于开展更多配置组合模式的研究, 覆盖范围更广;

3) BP-SGR预测模型计算时间更短, 速度更快, 可在争分夺秒的战场上快速制定符合实时作战情况的舰载机出动方案, 适用性更强, 灵活度更高。

4 SGR配置组合优化

SGR计算模型是进行SGR配置组合优化研究的基础, 前文已验证了BP-SGR预测模型作为SGR计算模型的可行性与必要性, 文中利用该模型进行SGR配置组合优化研究, 同时将验证优化结果的可信度。

文中考虑的资源配置参数范围如2.2节所述, 包含2 500种配置组合, 由于BP-SGR预测模型可快速计算任意资源配置组合的SGR, 因此在该研究范围内可利用枚举法在所有配置组合中寻找SGR最高的资源配置组合。

由于BP-SGR预测模型的计算结果不可避免与实际架次存在偏差, 因此无法保证该模型得到的最优SGR即为实际的最优SGR, 考虑到前文在验证该模型拟合效果时, 得到预测结果与仿真均值的平均相对误差为0.73%, 因此将基于该模型得到的最优SGR, 获取SGR误差范围小于0.73%的所有配置组合。计算得到的最优SGR为243.25, 在其0.73%误差范围内的最小SGR应为241.48, 经计算得到, 最高的前21组SGR在该范围内, 因此将该21组资源配置组合作为寻优结果, 同时对获取的计算结果采用3.4节描述方法进行二次验证, 判断其计算值可信度, 21组最优配置组合SGR结果如表3所示。

结果表明, 所有预测值均落在仿真值99%预测区间内, 仿真均值相对误差均小于1%, 因此认为BP-SGR预测模型可替代仿真SGR计算模型进行配置组合优化研究, 其优化结果可信。优化结果对应的配置组合如表4所示。

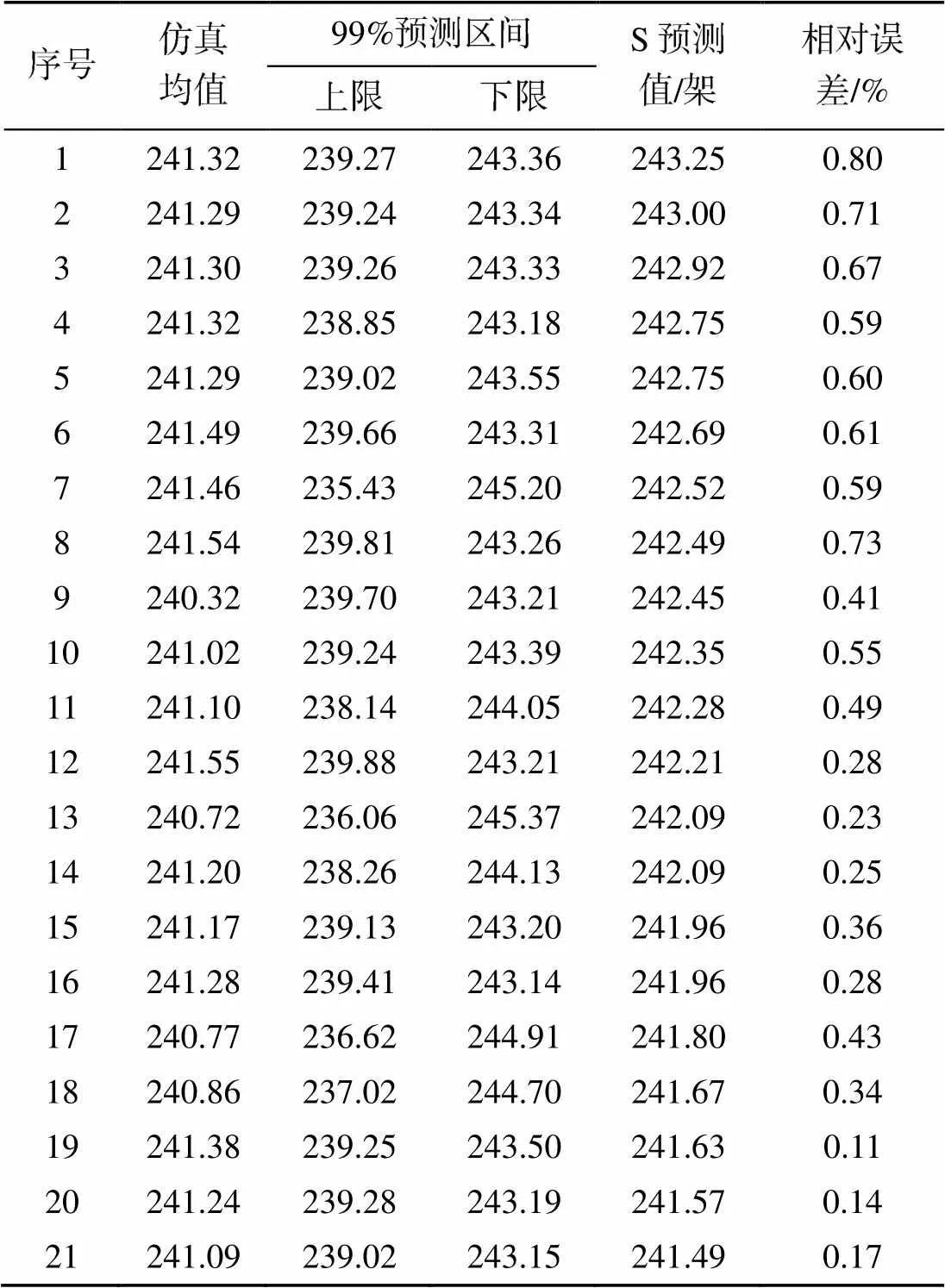
表3 前21组最优SGR结果

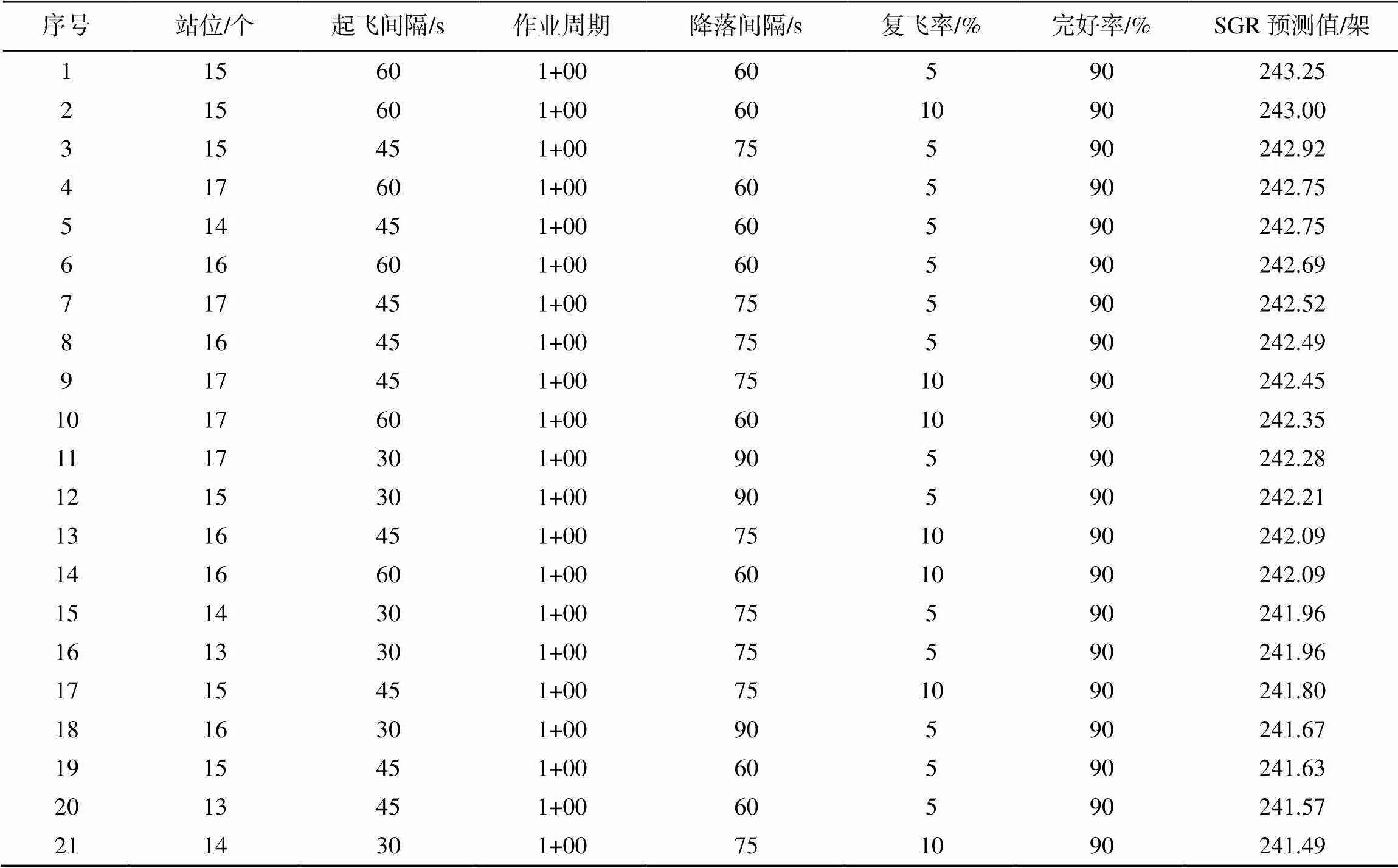
表4 前21组最优SRG配置组合

根据前21组最优SGR配置组合可以发现:

1) 21组最优配置的作业周期均为1+00, 说明在文中给定的参数范围内, 甲板作业周期选取1+00时, 更容易获得较优的SGR;

2) 21组最优配置的舰载机完好率均为90%, 说明在文中给定的参数范围内, 较高的舰载机完好率更容易获得较优的SGR;

3) 参数取值并不是绝对的越大越好或者是越小越好, SGR的高低与参数之间的组合方式相关, 因此在对航母资源进行配置时, 资源的组合方式应成为重点考虑因素之一。

5 结束语

为研究作战环境资源配置对于系统综合作战能力的影响, 文中以甲板舰载机为例, 研究不同甲板配置资源下的航母SGR, 对单周期波次出动流程进行了建模与仿真, 针对仿真模型需多次重复计算以降低结果随机性问题, 采用BP神经网络对仿真模型进行拟合, 得到BP-SGR预测模型。经验证, 该模型很好地反映了原仿真模型的行为, 可作为研究配置资源的SGR计算模型, 且可大幅降低计算次数, 提高模型的简洁度, 有利于开展更大范围的配置组合研究, 并快速制定符合实时战场的出动方案。最后利用该模型进行最优资源配置组合研究, 验证了其在此优化问题上的可行性, 优化结论表明, 除单一资源参数取值外, 资源组合方式也是影响SGR的重要因素之一。

文中提出的预测模型计算时间短, 计算结果准确度高, 适用性广, 适用于研究舰载机、无人艇等装备以波次作业模式执行任务时的作战能力及各资源的具体影响, 为研究资源配置对作战能力的具体影响提供了有益参考。由于所使用的仿真因素多为静态模型, 且资源参数粒度较大,下一步将考虑对可靠性、维修性参数及人员疲劳度等建立动态仿真参数模型, 并细化资源参数粒度, 对各资源进行敏感性分析, 研究其对SGR的影响程度及某种条件下的瓶颈资源。

[1] 刘相春. 航空母舰舰机适配性技术体系[J]. 中国舰船研究, 2016, 11(3): 1-4.Liu Xiang-chun. A Technology System for the Carrier/air Vehicle Integration[J]. Chinese Journal of Ship Research, 2016, 11(3): 1-4.

[2] 熊勇, 余嘉俊, 张加, 等. 无人艇研究进展及发展方向[J]. 船舶工程, 2020, 42(2): 12-19. Xiong Yong,Yu Jia-jun, Zhang Jia, et al. Research Pro- gress and Development Direction of Unmanned Aerial Ve- hicle[J]. Ship Engineering, 2020, 42(2): 12-19.

[3] Stillion J, Orletsky D T. Airbase Vulnerability to Conventional Cruise-missile and Ballistic-missile Attacks: Technology, Scenarios, and U.S. Air Force Responses[M]. Santa Monica, CA: RAND Corporation, 1999: 81-84.

[4] Harris J W. The Sortie Generation Rate Model[C]//The 2002San Diego, CA, USA: [s.n.], 2003: 864-868.

[5] 夏国清, 陈红召, 王元慧. 基于闭排队网络的飞机SGR分析[J]. 系统工程学报, 2011, 26(5): 686-693. Xia Guo-qing, Chen Hong-zhao, Wang Yuan-hui. Analysis of Sortie Generation Rate Based on Closed Queueing Network Model[J]. Journal of Systems Engineering, 2011, 25(5): 686-693.

[6] 郑茂, 黄胜, 赵永振, 等. 舰载机高峰出动仿真方法研究[J]. 武汉理工大学学报, 2013, 273(9): 61-66.Zheng Mao, Huan Sheng, Zhao Yong-zhen, et al. Simulation Research on Carrier based Aircraft Surge Operation[J]. Journal of Wuhan University of Technology, 2013, 273(9): 61-66.

[7] 陈成. 飞行甲板航空保障系统配置对SGR的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.

[8] Stammer R M. A Database Approach to Aircraft Carrier Airplan Production[R]. Monterey: Naval Postgraduate School, 1992: 76.

[9] 尹顾, 李杰, 雷湘平. 现代美国海军[M]. 北京: 国防大学出版社, 1995: 145-184.

[10] Angelyn J. Sortie Generation Capacity of Embarked Air- wings, ADA359178[R]. Alexandria, VA: Center for Naval Analyses, 1998.

[11] 刘相春, 卢晶, 黄祥钊．国外航母舰载机出动回收能力指标体系分析[J]．中国舰船研究, 2011, 6(4): 1-7.Liu Xiang-chun, Lu Jing, Huang Xiang-zhao. Analysis on the Index System of Sortie Generation Capacity of Embarked Aircrafts[J]. Chinese Journal of Ship Research, 2011, 6(4): 1-7.

[12] 林骥鹏. 基于离散事件的舰载机出动架次计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[13] 杨放青. 航母飞行甲板作业能力分析与优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.

[14] 陈练. 效率致胜——美国航母提高舰载机SGR新招数[J]. 现代舰船, 2008(10): 20-22.Chen Lian. Efficiency Wins: A New Way for American Carriers to Improve the Sortie Rate of Carrier Aircraft[J]. Modern Ships, 2008(10): 20-22.

[15] 刘相春. 美国“福特”级航母“一站式保障”技术特征和关键技术分析[J]. 中国舰船研究, 2013, 8(6): 1-5.Liu Xiang-chun. Technical Features and Critical Techno- logies for the “Pit-stop” Aircraft Servicing Adopted by Ford Class Aircraft Carriers[J]. Chinese Journal of Ship Research, 2013, 8(6): 1-5.

[16] 郜星军. 基于神经网络的股票预测模型[D]. 广西: 广西大学, 2019.

[17] 罗成汉. 基于MATLAB神经网络工具箱的BP网络实现[J]. 计算机仿真, 2004, 21(5): 109-111,115. Luo Cheng-han. Realization of BP Network Based on ne- ural Network Tool Kit in MATLAB[J]. Computer Simu- lation. 2004, 21(5): 109-111,115.

[18] 贾俊平, 何晓群, 金勇．统计学[M]. 4版. 北京: 中国人民大学出版社, 2009.

[19] 李泽阳, 刘玲, 胡奕仁. 基于预测区间理论的工程造价信息数据统计测算模型[J]. 统计与决策, 2018, 34(6): 29-32.Li Ze-yang, Liu Ling, Hu Yi-ren. Statistical Calculation Model of Engineering Cost Information Data Based on Prediction Interval Theory[J]. Statistics & Decision, 2018, 34(6): 29-32.

Calculation Model of SGR Based on Operational Environment Configuration Resources

PENG Ya-xin1, Huang Qi2, YU Ming-hui1, YANG-Jie1, SU Hou-sheng1

(1. School of Artificial Intelligence and Automation, Huazhong University of Science and Technology, Wuhan 430074, China; 2. China Ship Development and Design Center, Wuhan 430064, China)

The sortie generation rate(SGR) of naval weapons such as aircraft carriers and unmanned surface vessels (USVs) is the key index for judging the comprehensive operational capabilities of a system, where the resource configuration will greatly affect such a system. Therefore, research on the optimal combination of configuration resource of an operational system can improve the system’s operational capabilities. Using an aircraft carrier SGR as an example and based on the sortie-by-waves model, this study develops a simulation calculation model of the SGR. To avoid the problem of having to repeat the calculation to reduce the randomness of the results, a simulation calculation model is fitted by a back-propagation(BP) neural network, and a BP-SGR calculation model of is obtained. An optimization of the deck resource configuration with the BP-SGR calculation model is also studied. Through a simulation, all of the SGR combination values of 21 groups optimal resource configurations obtained by the BP-SGR calculation model fall within a 99% prediction range of the simulation model’s SGR calculation results. In addition, all relative errors are shown to be less than 1%, thus verifying the applicability of the model to resource configuration optimization. The BP-SGR calculation model can thus be used to solve configuration problems related to aircrafts and USVs.

naval weapon; sortie generation rate(SGR); resource configuration; sortie by waves; back propagation(BP) neural network

彭雅欣, 黄琦, 余明晖, 等. 基于作战环境配置资源的出动架次率计算模型[J]. 水下无人系统学报, 2020, 28(6): 642-649.

U674.771; TP183

A

2096-3920(2020)06-0642-08

10.11993/j.issn.2096-3920.2020.06.008

2020-06-01;

2020-07-26.

国家自然科学基金资助(61403255); 国防基础科研资助项目资助(2017207B005).

彭雅欣(1996-), 女, 在读硕士, 主要研究方向为航母作战、船舶设计、系统仿真与分析.

(责任编辑: 杨力军)