八国初中数学课程标准中根式与无理数的比较研究

甄祎明 康玥媛

摘  要：以中国、英国、韩国、芬兰、日本、美国、澳大利亚和新加坡八国初中数学课程标准中的根式与无理数内容为研究对象，利用NVivo11质性分析软件对其编码，在定性与定量分析的基础上得到我国数学课程标准中根式与无理数设置的一些启示：适度加大无理数的内容广度，在教学建议中加强数学史的渗透，进一步提出对根式与无理数的应用性要求.

关键词：根式;无理数;初中数学;课程标准;国际比较

[2]是数学史上的第一个无理数，它的出现引发了第一次数学危机，并推动数系由有理数扩充到了实数范围. 初中阶段，学生首次接触根式与无理数，掌握根式为其学习无理数提供前期经验，无理数的学习则有助于其深入理解根式中的不尽根问题，并且两者的学习能够帮助学生进一步认知数系. 然而，无理数概念属于超经验数学的范畴，学生难以获得不尽根式和无理数的现实经验，学生对两者的理解存在一定障碍. 课程标准是一个国家教学的指导性文件，其对内容的阐述会影响教师的教学，由此影响学生的学习.

近年来，课程标准的国际比较研究具有较高热度，将世界范围内具有代表性的课程标准进行横向比较，可以为研制本国课程标准、进行课程建设提供经验. 然而，综观国内的数学教育研究成果，相关课程标准研究多从宏观上分析“数与代数”相关内容，由此将根式、无理数等内容蕴含在整体分析中，少有研究聚焦于课程标准中的根式与无理数内容深入比较分析.

基于上述背景，对中国、英国、韩国、芬兰、日本、美国、澳大利亚和新加坡八国的初中数学课程标准中根式与无理数内容进行横向比较，并确定具体研究问题为：八国数学课程标准中根式与无理数的引入时间有何异同？八国数学课程标准中根式与无理数的内容广度如何？八国数学课程标准中根式与无理数的内容设置情况如何？

一、研究设计

1. 研究对象

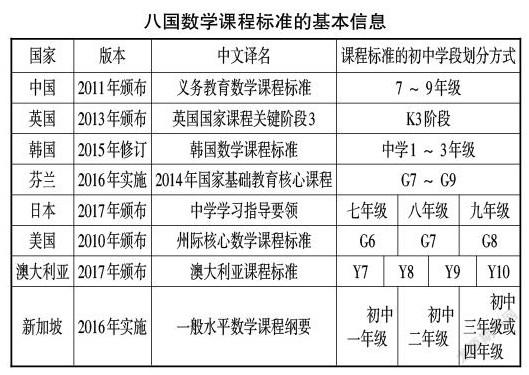
选取中国、英国、韩国、芬兰、日本、美国、澳大利亚和新加坡八国的初中数学课程标准为研究对象，所选国家的教育水平具有代表性，并且部分课程标准在近几年进行了新的修订，一些国家在国际大型测试PISA和TIMSS中表现优异，具有较高的参考价值. 其中，不同国家课程标准的内容划分方式不同，中国、英国、韩国和芬兰课程标准基于整个初中学段叙述课程内容，日本、美国、澳大利亚和新加坡课程标准则基于年级划分课程内容及相关要求，各国数学课程标准的基本信息如下表所示.

2. 研究方法与思路

研究利用NVivo11质性分析软件对八国课程标准中的根式与无理数内容进行编码，并根据编码结果，采用定性与定量相结合的方法进行比较研究. 具体研究思路为：首先，确定编码系统，将课程标准中根式与无理数所有相关内容整理统计，以内容知识点的形式高度概括;其次，进行编码，根据内容知识点，将课程标准中的内容条目以“最短整句”为单位进行编码;然后，编码信度检验，由两位研究者对课程标准文本进行独立编码，通过NVivo11软件的“编码比较（coding comparison）”对两份编码的一致性进行检验，结果显示，两位研究者对根式的编码一致性为93.92%，无理数的编码一致性为95.69%，说明研究的编码一致性程度较高，研究结果可靠;最后，整理分析编码结果并计算内容广度，根据统计结果，分别比较根式与无理数的引入时间、内容广度和内容设置，并做出定性与定量的分析.

在内容广度方面，曹一鸣将内容广度分为绝对广度、可比广度和相对广度三类，根据研究的主题，选取相对广度作为研究的内容广度模型，并将其界定为各国数学课程标准中知识点总量与八国最大值之间的比值.

二、研究结果及其分析

通过对八国课程标准中根式与无理数内容条目的编码，分别得到关于根式与无理数的引入时间、内容广度、内容设置三方面的比较结果.

1. 引入时间比较

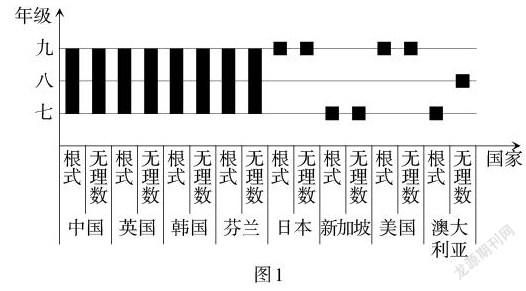
统计八国课程标准中根式与无理数内容的引入时间（如图1），可以发现，在根式的引入时间上，按学段分布的四国课程标准（中国、英国、韩国和芬兰）均在初中学段引入根式. 按年级分布的四国课程标准（日本、美国、澳大利亚和新加坡）中，澳大利亚和新加坡分别在Y7年级、初中一年级（均相当于我国七年级）引入根式，在四国中引入时间最早;美国和日本则分别在G8年级、九年级（均相当于我国九年级）引入根式，在四国中引入时间最晚. 在无理数的引入时间上，按学段分布的四国课程标准均在初中学段引入无理数. 按年级分布的四国课程标准中，新加坡在初中一年级（相当于我国七年级）引入无理数，引入時间最早;澳大利亚在Y8年级（相当于我国八年级）引入无理数;美国和日本则分别在G8年级、九年级引入无理数，在四国中引入时间最晚.

在引入顺序上，通过对课程标准文本的比较，发现八国课程标准均先引入根式，后引入无理数. 在根式与无理数的知识连续性上，大部分国家在同一学段或同一年级学习根式与无理数，只有澳大利亚出现了一年的年级间断.

2. 内容广度比较

对八国课程标准中根式与无理数内容的编码结果进行整理分析，得到内容知识点的统计结果，由此计算内容广度，并对其进行比较分析.

（1）根式的内容广度比较.

在初中阶段，根式多包含平方根和立方根两部分主要内容. 通过编码结果，发现八国课程标准在根式的知识点设置方面有较大差异，大部分国家对根式的阐述较少. 其中，四国设置“平方根的概念、平方根的表示”两个知识点，说明平方根是这些国家普遍重视的知识点;三国设置“平方根的开方计算、立方根的表示”;而“算术平方根、平方根的实际问题、二次根式、最简二次根式、乘方与开方的关系、计算器的使用”则分别只有一国设置，各国课程标准对此部分内容的设置较少关注.

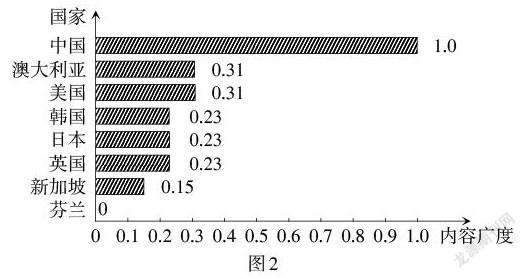
统计编码结果，得到八国课程标准的根式知识点共计17项，具体为：算术平方根的概念、算术平方根的表示、平方根的概念、平方根的表示、平方根的开方计算、平方根的四则运算、平方根的估值、平方根的意义、平方根的实际问题、立方根的概念、立方根的表示、立方根的开方计算、二次根式的概念、二次根式的四则运算、最简二次根式、乘方与开方的关系、计算器的使用. 结合各国课程标准中所含知识点的个数，计算得到八国课程标准中根式的内容广度（如图2）. 由图2可知，各国课程标准中根式内容广度的最值差距明显，并且其数值普遍较低. 在根式内容广度的比较上，内容广度最大的为中国课程标准，并且其数值远超八国广度均值（0.31）;内容广度最小的为芬兰课程标准，并且芬兰课程标准是八国中唯一没有提及根式内容的课程标准;其他六国的内容广度差异较小，大部分较为接近平均值（0.31）.

（2）无理数的内容广度比较.

通过编码结果，发现八国课程标准中对无理数的阐述普遍较少. 其中，四国设置了“无理数的概念”这一知识点，表明其对无理数概念理解的重视;而“比较大小、数轴表示、联系实际”三个知识点则各只有一国设置，说明此部分不是各国课程标准普遍关注的内容.

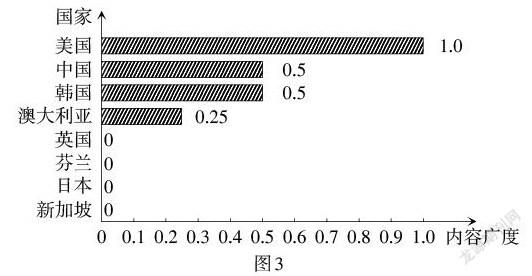
在编码结果的统计中，八国课程标准中提到的无理数相关知识点共计5项，具体为：无理数的概念、比较大小、数轴表示、联系实际、无理数的估值，数量相对较少. 通过计算八国课程标准中无理数的内容广度（如图3），可以发现，八国课程标准的无理数内容广度存在较大差异. 其中，内容广度最大的国家是美国，其次是中国和韩国，再次是澳大利亚，并且其内容广度与八国平均值（0.28）相近，而英国、芬兰、日本和新加坡四国课程标准没有提及无理数相关内容，其无理数内容广度为0，在八国中排名靠后.

3. 内容设置比较

（1）根式的内容设置比较.

我国课程标准强化根式内容的地位，其内容广度高出平均值近70个百分点. 其中，我国比其他国家多设置的内容条目有“算术平方根的概念、算术平方根的表示、二次根式的概念、二次根式的四则运算、最简二次根式、乘方与开方的关系、计算器的使用”7项内容条目;比其他国家缺少“平方根的估值、平方根的意义、平方根的实际问题”3项内容条目.

通过分析课程标准文本对根式内容的阐述，发现在根式的内容设置方面，各国多对“平方根与立方根的概念、表示方法、计算”进行阐述. 特别的是，我国课程标准对二次根式相关内容及计算器的使用进行阐述，提出对多种形式根式的计算要求. 日本课程标准提出“平方根在实际问题中的应用”要求，日本和韩国的课程标准提出对“平方根意义”的理解，英国和澳大利亚两国则提出“对平方根的估值”. 总体上，相较于中国，这些国家更为注重根式在内涵理解和知识应用层面的要求.

（2）无理数的内容设置比较.

在无理数的内容设置上，美国课程标准中无理数的内容广度高出平均值近70个百分点，比其他国家多设置的内容条目有“大小比较、数轴表示”2项内容条目;比其他国家缺少“联系实际”1项内容条目.

通过分析课程标准文本对无理数内容的阐述，发现在无理数的内容设置方面，各国课程标准多对无理数的概念理解提出要求. 而美国课程标准还提出“无理数的数轴表示、估计表达式的值、用有理数逼近無理数”等要求，这样的内容设置有助于学生深刻理解无理数是无限不循环小数的概念内涵，并由此渗透逼近思想. 此外，韩国课程标准提出“平方根和无理数可以利用毕达哥拉斯定理引入;利用边长为1的正方形的对角线长度等，直观地理解无理数的存在”，这样的表述顺应了无理数的历史发展脉络，有助于学生正确建立无理数概念，由此为数系扩充的学习打下坚实的基础. 总体而言，相较于中国，这些国家更注重学生对无理数的概念内涵、产生过程的理解.

三、研究结论及启示

基于以上研究结果，得到如下研究结论.

其一，在引入时间上，八国课程标准根式与无理数的引入时间具有较强的一致性，普遍先引入根式、后引入无理数，并且两者的引入时间具有连续性.

其二，在内容广度上，八国课程标准的根式内容广度普遍较低，无理数的内容广度最值差距明显，呈现出“两极分化”特征. 总体而言，与根式相比之下，八国课程标准中的无理数内容条目均较少.

其三，在内容设置上，八国课程标准中根式与无理数的内容设置则各具特色，并主要体现为对内涵理解、知识应用、产生过程的关注.

基于以上结论，对我国课程标准中根式与无理数的设置提出如下建议.

1. 适度加大无理数的内容广度

通过对课程标准文本的分析，发现相较于无理数，我国的根式知识点数量约为无理数知识点数量的六倍，而无理数是实数中的重要内容，甚至是实数系扩充的关键内容，课程标准对无理数的关注将影响到教师对无理数内容的重视程度，进而影响到学生对此部分内容的学习效果. 在历史上，无理数的发现引发了第一次数学危机，并推动了数系的扩充，其在数系中的重要性与地位不容忽视. 我国课程标准在重点强调根式内容、构建知识网络的同时，也应注意对各部分内容做出更加全面的要求. 在新课程标准的修订中，我国课程标准可考虑适当增加无理数的内容占比，并细化其内容条目，丰富其内容要求，由此强化无理数的重要地位，协调课程标准中根式与无理数的内容广度.

2. 在教学建议中加强数学史的渗透

历史上，人类对无理数的认识从“根号型”开始，并且无理数从出现到被广泛接受经历了相当长的时间，根据人类学习的历史相似性，学生对无理数的接受和理解存在较大的困难. 韩国课程标准提出“以正方形的对角线直观地理解无理数”的教学与学习建议，则顺应了数学史脉络，较为具体地给出了教学设计示例，这样的教学过程有助学生体验知识的产生过程并从中渗透数学文化. 我国课程标准可以考虑在教学建议中加强对数学史的关注，并将建议具体化，从而利于教师准确把握课程标准的意图，使学生有机会更广泛地了解知识的发生背景、原因及过程，启发其思考知识的内在联系，从而在宏观上把握实数系的发展脉络，在微观上理解根式与无理数之间的密切联系.

3. 进一步提出对根式与无理数的应用性要求

情境能够激发学生的学习兴趣、促进其数学理解，国际项目PISA的历次测评框架均体现出其对真实情境的关注，强调个体利用数学知识解决问题的能力，并注重学生应用能力的发展. 通过比较发现，在根式与无理数的阐述中，日本和韩国课程标准均对相关内容在实际问题中的应用提出要求，注重对学生应用意识的培养，而我国课程标准没有提及相关要求. 应用知识解决实际问题，是推动数学不断发展的重要因素之一，更是新时代人才必备的核心能力. 我国课程标准可以考虑提出对根式与无理数的应用性要求，强化知识的实用价值，并拓展教学资源，指引教师进一步挖掘生活中的素材，甚至是跨学科的应用，从而使学生在实际问题的解决中体会根式、无理数引入的必要性，在知识的感悟、形成、发展过程中体会其应用价值.

参考文献：

[1]张奠宙，王华，司擎天. 无理数教学三人谈：超经验数学研究之一[J]. 数学教学，2015（8）：封2，1-2.

[2]杨慧娟，郭蓉蓉，孟梦，等. 中韩小学数学教材中分数除法的比较研究[J]. 数学教育学报，2020，29（2）：64-69.

[3]彭艳贵.“中国”“美国”“新加坡”“英国”“澳大利亚”高中数学课程标准复数内容比较研究[J]. 数学教育学报，2019，28（1）：49-54.

[4]黄思婷，朱哲. 中日初中学段数学课程标准“数与代数”比较研究[J]. 中小学教师培训，2019（7）：75-78.

[5]严虹，曹一鸣. 基础教育阶段数学课程内容设置的国际比较研究：基于六国“数与运算”课程内容的研究[J]. 教育学术月刊，2017（4）：96-103.

[6]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[7]曹一鸣. 高中数学课程标准的国际比较研究[M]. 上海：上海教育出版社，2017.

[8]黄友初. 数学史对职前教师教学知识影响的质性研究：以无理数的教学为例[J]. 数学教育学报，2017，26（1）：94-97.

[9]李健. 初中数学教科书中现实问题情境设置的实证研究：基于中外九版初中数学教科书的纵向与横向比较[D]. 天津：天津师范大学，2019.

[10]曹一鸣，朱忠明. 变与不变：PISA2000—2021数学测评框架的沿革[J]. 数学教育学报，2019，28（4）：1-5.