基于惯性释放方法的某型电动轮自卸车车架结构性能分析

肖学文，刘金华，张 栋，米承继，李文泰

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

电动轮自卸车作为大型露天矿山场所的主要运载装备，其运载质量大、工作时间长，且矿山路面凹凸不平，致使其运行环境十分恶劣[1-2]。车架作为主要承载部件，其结构性能直接影响着整车的安全性能[3]。车架在实际工作过程中承受复杂的边界条件，且在传统方法下车架结构的受力、约束和变形状态等边界条件对有限元分析有重大的影响[4]。传统有限元的车架强度分析，通常是建立轮胎与地面的连接关系，并约束其连接点，相关研究表明，约束点的反力矩会改变结构实际受力状态，致使其结构应力与实际受力间的误差较大[5]。有些研究者使用弹簧单元模拟悬架系统，则需要知道其阻尼值和刚度值，但是实际过程中主要是依靠经验进行设计。而惯性释放法不需要这些约束条件，主要是根据结构质量创建一个惯性力平衡载荷力系，进而求解力学响应条件[5-8]。因此，为解决上述问题，本研究拟采用惯性释放方法对不同工况下的车架结构进行力学性能分析。

惯性释放方法具有在边界条件不确定的情况下，仍能计算出结构的任意响应的优势，因此，诸多学者对它开展了相关研究。为提高新能源车车架强度分析精度，孙辉等[5]基于多体动力学联合有限元分析法，提取了整车在多工况下的车架连接点处的载荷，并通过惯性释放法对车架进行了强度分析。Shen B.S.等[6]采用惯性释放和子模型的方法，对轿车平衡轴的7 种工况进行了接触非线性强度分析。阎琨等[7]将改进的惯性释放法与等效静力法的优化思想和混合胞元自动机法的材料更新规则结合，提出了一种运用在汽车耐撞性拓扑优化问题上的混合法。赵婷婷等[8]利用惯性释放法，对某微型货车车身进行了静态分析，得到其车身应力分布，并结合MSC.Fatigue 软件进行白车身的疲劳分析。目前，基于惯性释放法方面的研究，主要研究对象是轿车的车身，而对于大型的电动轮自卸车车架的应用研究相对较少，因此本研究选取大型的电动轮自卸车车架为研究对象，以期为今后的相关研究提供参考。

模态分析和频率响应分析是车架结构动态特性分析的关键，也是评价车架结构安全性能的重要方法。黄妮等[9]以氢燃料电池客车车架作为研究对象，运用HyperWorks 软件对其进行了模态分析和频率响应分析。刘闯等[10]建立了某轻型客车真空盒支架的有限元模型，并对其进行了材料分析、装配分析、断口分析以及动态频率响应特性分析，确定其支架断裂的原因为在激励频率下发生共振，共振时最大应力远大于材料的屈服极限，从而导致支架断裂。

综上所述，为了研究电动轮自卸车车架在不同边界条件下的结构力学性能，本研究首先建立了车架有限元模型，然后采用惯性释放方法对车架强度进行了分析；其次，将其应力结果与试验结果进行对比分析，在保证车架数值模型准确性的基础上，对车架开展模态分析和频率响应分析，研究车架结构的动态特性，以期为电动轮自卸车车架设计提供参考依据。

2 惯性释放方法

惯性释放方法的原理，是通过结构本身的质量，在外部载荷激励下产生惯性力，构造平衡力系和力矩力系微分方程，使其处于静止平衡状态或是匀加速状态，模拟非约束状态下结构的响应分析[11]。常运用于飞机、轮船、汽车等无约束状态下或者复杂约束下的静力分析，相较于传统的固定约束，能够较好地消除边界约束点反力所产生的应力集中的影响，得到较为合理的计算结果[5]。

图1 为微单元体下载荷分量以及加速度分量示意图，惯性释放法中自平衡微分方程中载荷向量以及加速度向量公式如下。

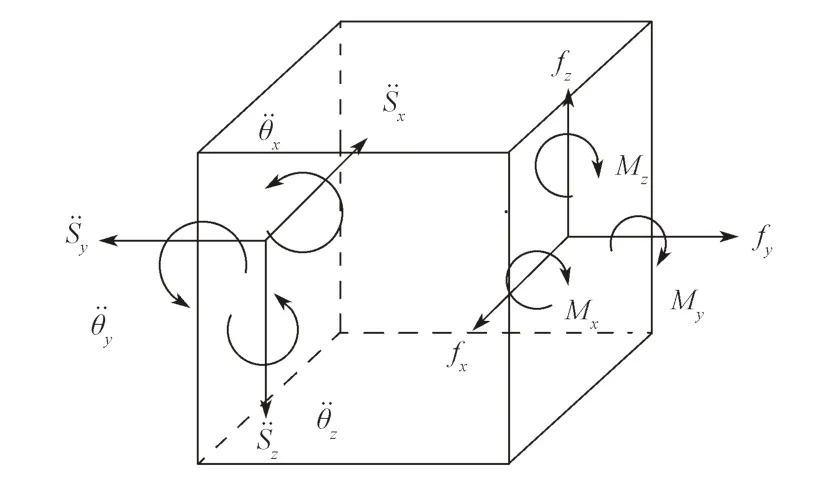
图1 微单元体的分量示意图Fig.1 Schematic diagram of the components of a microelement body

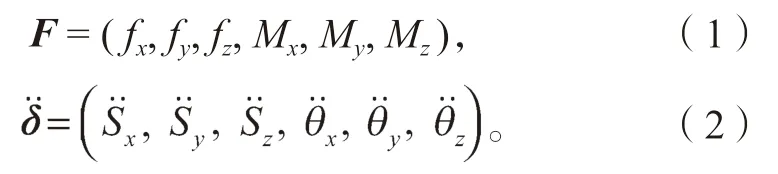
式（1）（2）中：F 为节点外载荷向量；fx、fy、fz为任意一点所受载荷在x、y、z 轴上的投影分量；Mx、My、Mz为任意点所受弯矩在x、y、z 轴上的投影分量；为节点加速度向量；、、为任意一点的线加速度在x、y、z 轴上的投影分量；、、为任意一点的角加速度在x、y、z 轴上的投影分量[11]。

根据运动学和力系平衡关系，可得惯性释放静动力平衡方程[12]为

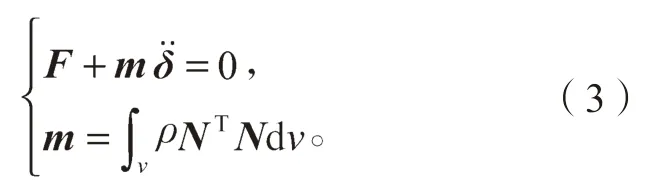
式（3）中：m 为质量矩阵；v 为体积分；ρ 为材料密度；N 为形态矩阵。

通过对上述公式的求解，可以得到任意节点达到平衡时的节点加速度，进而获得任意节点处的惯性力，再将惯性力作为外力施加在有限元的相应单元节点上，最终无需约束边界条件构造一个自平衡力系。在车架有限元计算过程中，消除了约束点的反力引起的变形和应力集中的影响，从而使得分析结果更加符合实际情况。

3 车架有限元模型的建立

电动轮自卸车作为大型露天矿场的主力运输装备，主要包括发动机-动力总成、发电机、冷却系统、驾驶室、燃油箱、驱动电机等主要部分，其三维模型见图2。车架有限元模型的构建和hypermesh 网格离散化的细节以及验证过程参考之前的研究成果[13]。限于篇幅，此处不再赘述。车架主要受到两方面的载荷：悬上载荷和悬下载荷。为了更接近实际工况，在车架悬上的装备质量采用mass 单元模拟，通过reb3单元将mass 单元在质心和车架接触处，建立的车架有限元模型如图3 所示。车架悬上主要部件质量分布如表1 所示。

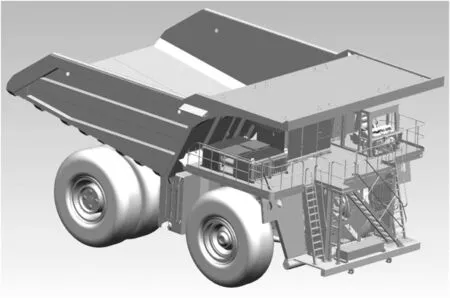
图2 电动轮自卸车三维模型Fig.2 Three-dimensional model of electric wheel dump truck

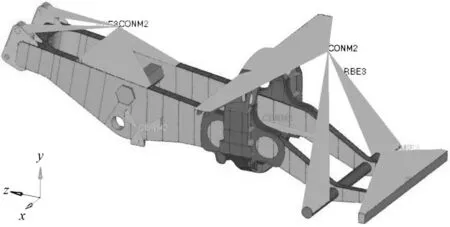
图3 车架有限元模型Fig.3 Frame finite element model

表1 车架悬上主要装备质量Table 1 Quality of main equipment on frame suspension

4 载荷工况及边界条件

电动轮自卸车在运动过程中还需要考虑来自地面的激励，这部分激励主要通过轮胎传递至悬挂系统，再由悬挂系统传递到车架的前后悬挂铰接处，属于悬下载荷。对车架进行不同工况分析时需要输入不同载荷，因此获取其铰接处的载荷十分重要。由于电动轮自卸车十分庞大且属于非公路工程车辆，不容易获取其在不同工况下的悬下载荷，为了获得整车对于不同工况的动态响应，考虑地面摩擦、悬挂系统阻尼和刚度，以及轮胎刚度，因此在ADAMS（automatic dynamic analysis of mechanical systems）软件中需借助电动轮自卸车多体动力学模型模拟其在不同工况下行驶。参考文献[14]，从中分别提取满载工况下的凹坑凸台工况、直线上坡工况、上坡转弯工况、下坡转弯制动工况下，车架前后悬架铰接处的x、y、z 方向的最大载荷值。4 种工况下的载荷分布如表2 所示。

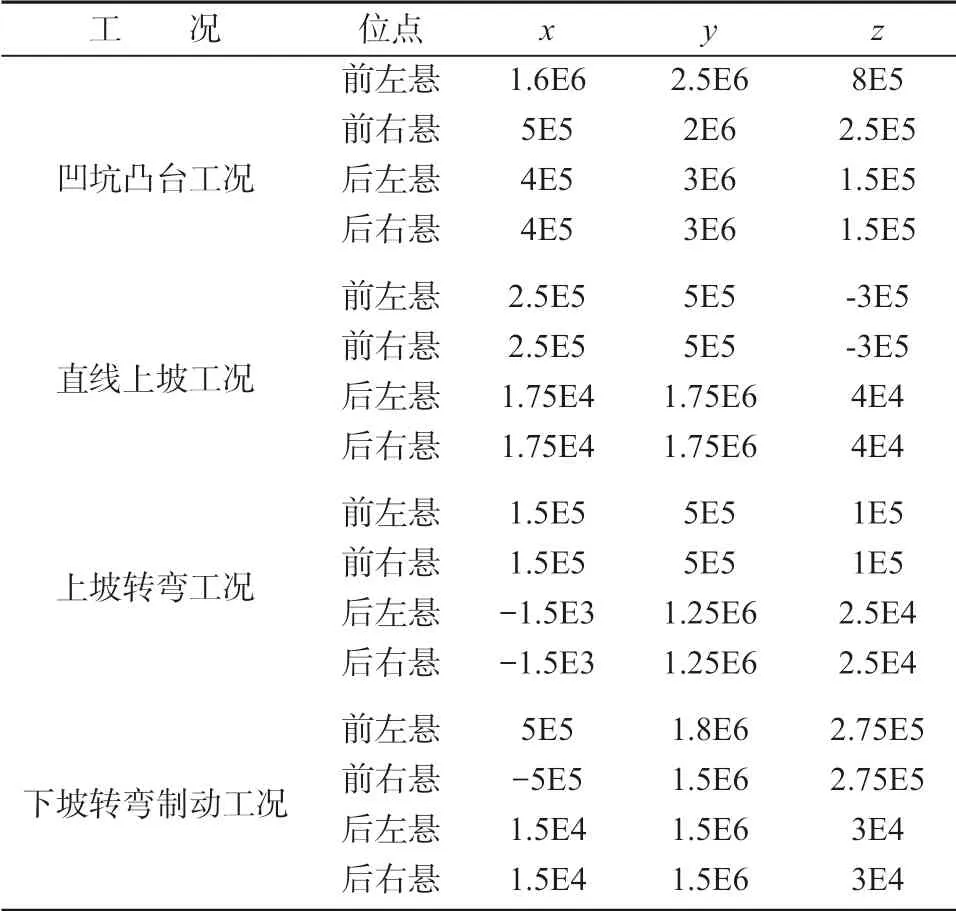
表2 不同工况下车架悬挂铰接处载荷值Table 2 Frame suspension hinged joint loading under different working conditions N

5 车架结构强度分析与应力对比分析

在上述有限元模型的基础上，采用惯性释放方法对车架进行静力分析，此时需要对一个节点6 个自由度虚约束，通常选择在车架质心位置，将虚约束通过reb2 耦合至车架悬架上。基于hypermesh 中Optistruct 求解器分别对车架在4 种工况下进行强度分析，所得结果如图4 所示。多工况下的试验数据参考文献[15]，其车架测点1～5 的分布如图5 所示，并将有限元分析结果与整车满载多工况下的试验数据进行了对比，如表3 所示。

图4 4 种工况的车架应力云图Fig.4 Stress cloud diagram of the frame under four working conditions

图4a 为车架满载凹坑凸台路面匀速行驶工况下的应力云图。从图中可以看出，车架的最大应力为399.5 MPa，出现在纵梁下面板与纵梁后板两板相交处，这是由于后轮在通过凸台时，路面给后悬架的脉冲载荷输入，导致车架弯曲变形，且此处存在几何形状的突变。图4b 为车架满载直线上坡工况，上坡时前后悬架所受的悬上载荷会重新分配，车架后悬挂处所受载荷增加。因此，最大应力同样出现在纵梁下面板与纵梁后板两板相交处。图4c 为车架满载上坡转弯工况，同样，由于悬上载荷的重新分配，导致车架右后轮处载荷以及相应区域应力增加。图4d 则是由于整车在下坡时转弯制动，导致车架所受载荷集中在前悬处。图4 所示的4 种工况下车架应力分布合理，且最大应力均未超过车架材料的允许应力。

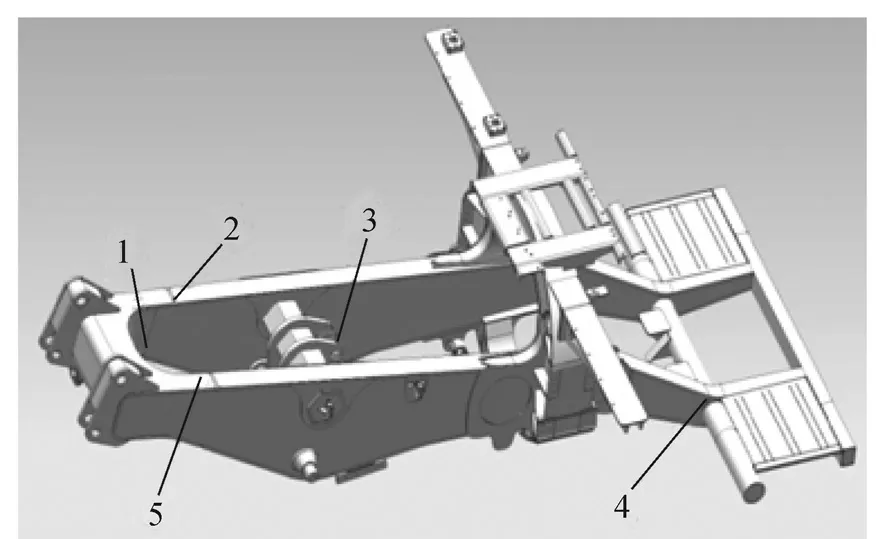
图5 车架测点分布图Fig.5 Distribution of frame measuring points

表3 多工况下车架应力仿真值与试验值对比Table 3 Comparison of the simulation and test values of frame stress under multiple working conditions

由表3 可知，测点3 的误差最大达46.6%，其主要是模型在网格离散化时忽略了测点3 处的后桥壳与车架连接部分结构，并且其加载导致受力形式与实际情况不完全相同。而测点4 的最大误差达到81.7%，其主要原因是各车架有限元模型分析时，对其进行简化，没有考虑车架甲板与前横梁处的焊接以及存在的几何过渡，从而使得仿真结果与试验结果之间误差较大。此外，其它测点仿真结果与试验结果相对误差较小，应力值与试验测试值分布趋势一致，表明采用惯性释放方法能得到较合理的应力分布。

6 车架模态分析与频率响应分析

6.1 模态分析

模态是结构的固有特性，通过模态分析可以确定结构的固有频率和振型[10]。车架作为电动轮自卸车的主要承载部件，不仅需要满足强度要求，还需要避免设计的车架结构在工作中产生共振。由于车架在工作状态的边界条件复杂，因此本研究中对车架进行自由模态分析。通过hypermesh 中Optistruct 求解器进行求解，采用Lanczos 法进行分析以节省计算时间，在此情况下车架的前6 阶模态为刚体模态，并无实际意义，因此本次计算结果剔除前6 阶刚体模态，将车架第七阶模态作为第一阶模态，所得模态阶数往后以此类推。最终计算得到车架模态的前10 阶模态频率和振型，如表4 所示，限于篇幅，仅列出车架模态的前4 阶模态振型，如图6 所示。

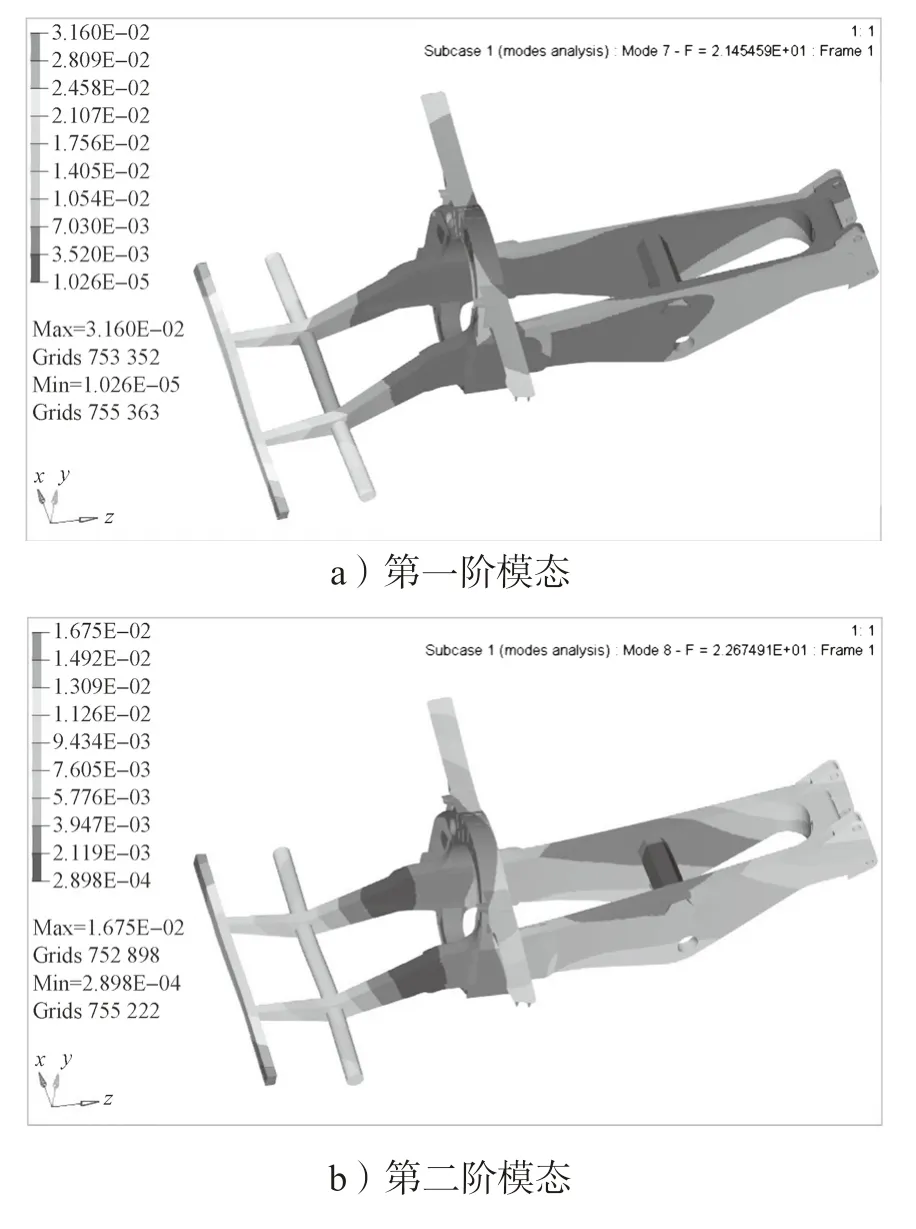
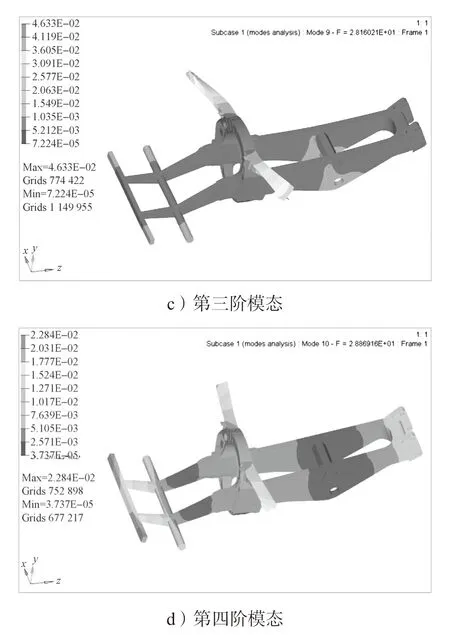
图6 车架模态分析图Fig.6 Frame modal analysis diagram

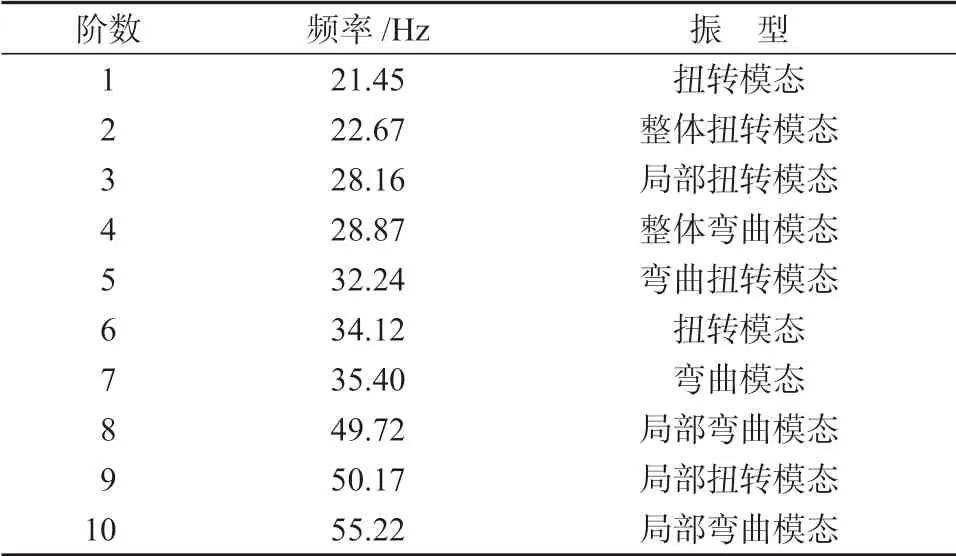
表4 车架前12 阶模态计算结果Table 4 Calculation results of the first 12 modes of the frame

一般情况下车架受到来自路面的激励主要集中在20 Hz 的频率内，受到发动机的激励频率为63 Hz[16]。由图6a 和表4 可知，车架模态振型平整，没有明显突变。车架一阶模态固有频率为21.45 Hz，振型为扭转模态，一阶固有频率略大于路面激励频率且远小于发动机激励频率，可知该车架结构有效避免了主要外载荷激励源频率可能导致的共振问题。

6.2 频率响应分析

频率响应分析是对结构动态特性的一种预测，通常是分析其结构在按照特定规律变化下频率的响应值曲线[16]。对车架进行频率响应分析，能够了解其动力特性，规避共振和消除受迫振动带来的影响。频率响应分析方法包括直接频率响应分析和模态响应分析，考虑车架模型复杂，因此选择对车架模态频率进行响应分析。对车架4 个悬架铰接处加上单位力载荷，设置扫频范围为1～50 Hz，结构阻尼系数为0.01[17]。通过hypermesh 中Optistruct 求解器进行求解，最终得到单位载荷下4 个悬架铰接处的位移和等效应力频率响应曲线，如图7 所示。

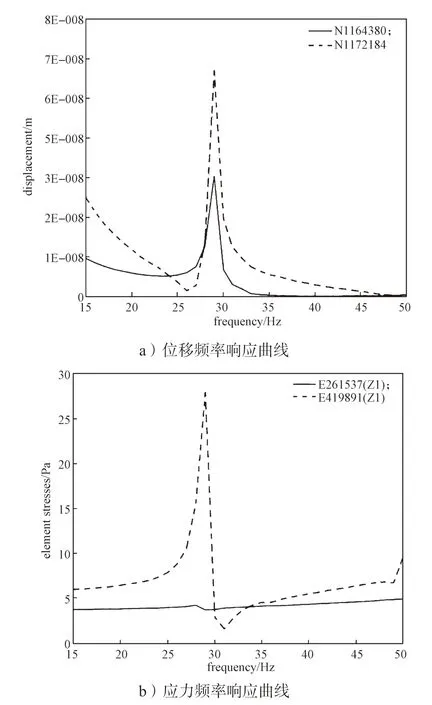
图7 车架频率响应分析图Fig.7 Frame frequency response analysis diagram

从车架位移频率响应曲线图7a 可以得知，其中N1164380 和N1172184 节点分别为前悬铰接处危险点与后悬铰接处危险点，当作用在前后悬架的激振频率达到29 Hz 时，车架发生共振，其悬架处位移响应激增，容易在此处发生塑性变形。从应力频率响应曲线图7b 可知，由于在此应力频率响应分析云图中只能选择网格单元，因此选择应力变化较大的E261537与E419891 单元。其中E261537 为后悬铰接处应力变化较大单元，可以看出其在激振频率为28～29 Hz时产生应力波动。其中E419891为前悬铰接处危险点，在激振频率为29 Hz 时，其应力响应剧增，这会导致车架局部应力过高，从而产生破坏。车架在29 Hz 时位移响应和应力响应较大，与模态分析中车架第四阶固有频率基本相同，从而引起车架共振。但是与车架所受路面、非弹簧载部件、发动机等激励频率没有发生重叠，有效地避免了共振的发生。

7 结论

本研究对电动轮自卸车车架进行了结构力学性能分析，首先，以多体动力学模型模拟不同工况下车架悬架处载荷作为载荷边界条件输入，在凹坑凸台、直线上坡、上坡转弯、下坡转弯制动工况下，基于惯性释放法对无约束的车架进行强度分析，并与试验数据进行了对比。其次，选用Optistruct 对车架进行了模态分析。最后，基于车架模态分析的基础上，对车架有限元模型进行了频率响应分析。可得出如下结论：

1）基于惯性释放法，对车架的4 种工况下的应力与实车在实际路面下的试验结果进行了对比，得知绝大部分测点仿真结果和试验结果的相对误差在10%以内。

2）采用惯性释放法能够减少传统约束处的应力集中现象，更为真实地显示车架的应力分布，并且车架整体结构应力均未超过抗拉强度。

3）对车架进行自由模态分析，得出车架前10 阶模态的固有频率和振型，其中一阶模态的固有频率为21.45 Hz。在此基础上，进行了频率响应分析，得出车架最大频率响应激振频率为29.0 Hz，未与主要激励源频率重叠，有效避免了车架共振现象的发生，车架整体结构力学性能达到工程要求。