非对称悬臂施工曲线连续刚构桥不同施工阶段应力变化规律研究
2021-01-13杨果林谭文杰周伏良
杨果林,黎 勇,谭文杰,周伏良
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中建五局 土木工程有限公司,湖南 长沙 410004)
0 引言
随着我国经济社会的飞速发展,以及西部大开发、一带一路战略的提出,基础设施建设不可避免地会向高原和山地等地方延伸。但是在高原或山地进行桥梁建设时,因路、桥交叉的原因,需要实现三维跨界工程,而采用曲线连续刚构桥是实现三维跨界工程的主要桥型之一。
在桥梁工程中,曲线连续刚构桥有着可以避免占用土地和节约建筑费用的优点[1-2]。但是曲线连续刚构桥的受力要比直线型桥的受力复杂得多,因其存在“弯扭耦合”作用,主梁截面拉应力会比直线型桥大得多,同时会受扭矩的作用而产生扭转变形。非对称曲线连续刚构桥属于曲线连续刚构桥的一种,因结构的非对称性,会使其主梁的受力更为复杂,因此分析曲线梁的空间受力对于非对称曲线连续刚构桥在施工过程中的应力控制非常重要。
目前,对于曲线连续刚构桥的受力特性,许多学者进行了研究[3-12]。如田雪峰[3]对曲线连续刚构桥在恒载作用下的受力进行了分析,得出了主梁上侧处于受拉状态,下侧处于受压状态的结论;黄斌等[5]对曲线连续刚构桥施工阶段的结构受力进行了分析,得出了主梁全截面均受压的结论。但目前对非对称曲线连续刚构桥的受力研究相对较少,因此本文以湖南省长沙市桐溪路景观桥为依托工程,研究非对称曲线连续刚构桥在不同施工阶段的应力变化规律,以期为非对称曲线连续刚构桥梁的施工控制提供理论依据。
1 工程背景
湖南省长沙市桐溪路景观桥位于大王山旅游度假中心桐溪路,为长沙市坪塘工矿棚户区改造暨旅游产业中心区项目基础设施重点工程,属于坪塘大道—潇湘大道东线道路工程中的一段,桥梁起点桩号为K0+413.793,终点桩号为K0+706.793。桐溪路景观桥为15.0 m+55.5 m+145.0 m+55.5 m +15.0 m 的预应力混凝土连续刚结构,其主线宽22.6 m,景观平台宽5.3 m,属于新建桥梁。桐溪路景观桥的主桥布置见图1,图中桥结构数据单位为cm。因为该工程位于岩溶发育地区,所以在设计中采用曲线桥穿越矿坑,桥梁平面曲线半径为600 m,主桥平面图见图2,应力测试关键截面见图3,图中数据单位为cm。

图1 主桥布置图Fig.1 Layout of the main bridge

图2 主桥平面图Fig.2 Planar graph of the main bridge

图3 应力测试关键截面图Fig.3 Key sections of stress tests
桐溪路景观桥上部结构采用145 m 连续刚构桥,主梁为混凝土箱梁结构,箱梁类型为单箱双室,桥面设置为双向坡,坡度为1.5%。箱梁底板宽度为14.6 m,悬臂端宽度为4.0 m,顶板宽度为22.6 m,中跨跨中箱梁高度为3.2 m,边跨等截面箱梁高度为3.75 m,梁高均按1.8 次抛物线变化。
桐溪路景观桥采用挂篮悬臂现浇法进行对称及非对称施工,0#梁段采用托架现浇完成,其余各梁段采用挂篮悬臂浇筑,主梁合拢顺序为先边跨后中跨合拢。中跨悬臂浇筑的分块编号如图4 所示,图中数据单位为cm;边跨悬臂浇筑段的分块编号如图5 所示,图中数据单位为cm。
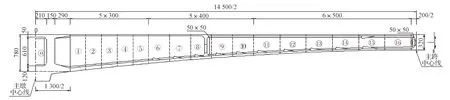
图4 中跨梁段分块编号Fig.4 Mid span beam segment block numbers
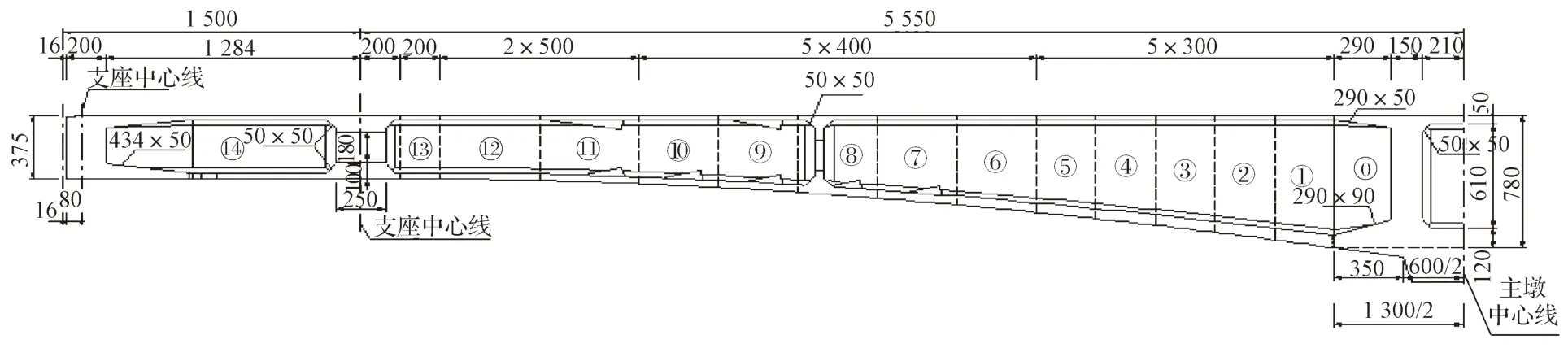
图5 边跨梁段分块编号Fig.5 Block number of side span beam section
2 非对称曲线连续刚构桥有限元模型
2.1 有限元模型的建立
采用有限元软件Midas/civil 建立曲线连续刚构桥模型,全桥共有110 个单元和122 个节点,具体如图6 所示。该桥的整体坐标系以跨中梁段对称面为坐标系的yoz 平面;原点取对称面与道路中心线的交点,即对称面的中点;x 轴取对称面的法线方向,从2#主墩指向3#主墩;y 轴指向背离曲线圆心的方向;z 轴指向上方。
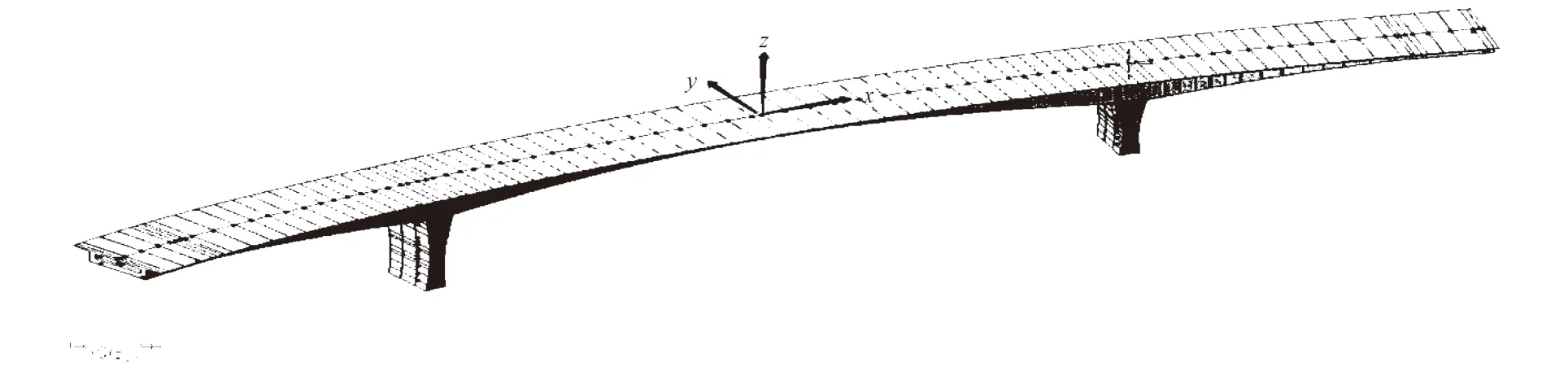
图6 曲线连续刚构桥桥梁模型Fig.6 Curved continuous rigid frame bridge model
建模时,2#、3#主墩底部采用固结约束,边跨桥头端部0#、1#、4#、5#桥墩处设置横向双支座,除水平轴向位移和竖向角位移外,对其他所有自由度进行约束。为了更好地模拟不同施工阶段的变形状态,本桥模拟遵循现场施工阶段进行,对各个阶段的应力进行计算及分析。施工阶段划分见表1。

表1 施工阶段划分Table 1 Construction stage division
2.2 关于“非对称”含义的说明
本研究中桥梁以主墩为界,则边跨侧的桥梁长度为0.5×1 300 cm+5×300 cm+5×400 cm+2×500 cm+200 cm+1 684 cm =7 034 cm,而中跨侧的桥梁长度为0.5×1 300 cm+5×300 cm+5×400 cm+6×500 cm+0.5×200 cm=7 250 cm,两者相差216 cm,因此中跨16#梁段和中跨合拢段在边跨侧没有对应梁段,称为非对称梁段。
实际施工过程中,中跨和边跨各自0#~11#梁段的长度、截面、张拉纵向预应力束相同,但是边跨侧12#梁段混凝土用量为98.6 m3,而中跨侧12#梁段仅用73.3 m3,这导致两个梁段质量存在差异。边跨13#合拢时,中跨对应部分还未开始施工,边跨现浇部分和挂篮施工部分通过边跨后期束连为一体,共同受到边跨支座的约束。
边跨支座设置后,中跨13#梁段继续使用挂篮施工,此时主墩两侧桥长度不同,所受约束条件不同,梁段之中施加的纵向预应力钢束也不同,因此此阶段在约束条件上也是不对称的。
此外,2#主墩和3#主墩的墩高分别为24 m 和18 m,墩高不同可能会造成桥梁对称位置的计算结果出现差异。
3 模型计算结果与分析
2 号墩2 号截面、3 号截面和4 号截面为桐溪路景观桥的关键截面,故选取2 号墩2 号截面、3 号截面和4 号截面在施工过程中的应力进行分析,所得结果如图7~9 所示。图中负数表示压应力,正数表示拉应力。
2 号截面位于2 号墩边跨,2 号墩边跨属于对称施工阶段,其应力分析结果见图7。
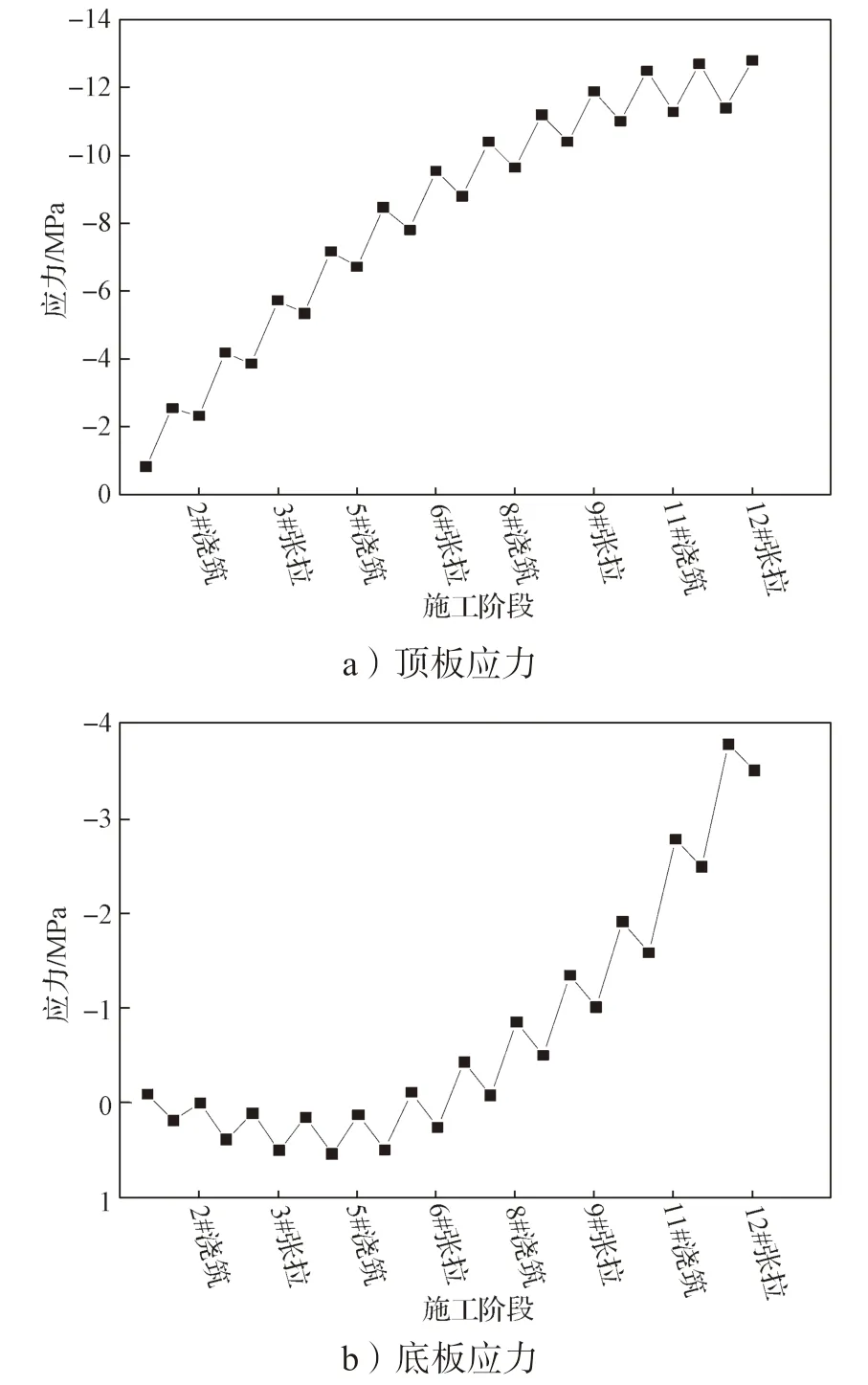
图7 2 号截面应力结果分析图Fig.7 Stress result analysis of section 2
如图7 所示,在对称施工阶段,箱梁顶板的应力随着悬臂长度的增加而增大,预应力钢筋张拉会引起箱梁顶板的应力增大,箱梁顶板最大压应力为12.8 MPa;箱梁底板应力在0#梁段至边跨8#梁段施工时,箱梁底板承受的应力为拉应力,且拉应力会随着悬臂长度的增加而增大。在9#梁段至12#梁段施工时,箱梁底板的应力由拉应力转换为压应力,且压应力随着悬臂长度的增加而增大;预应力钢束张拉会引起箱梁底板应力的增大,2 号截面箱梁底板的最大拉应力为0.545 MPa,最大压应力为3.52 MPa。
3 号截面位于2 号墩中跨,2 号墩中跨包含对称施工阶段及非对称施工阶段,其应力分析结果见图8。
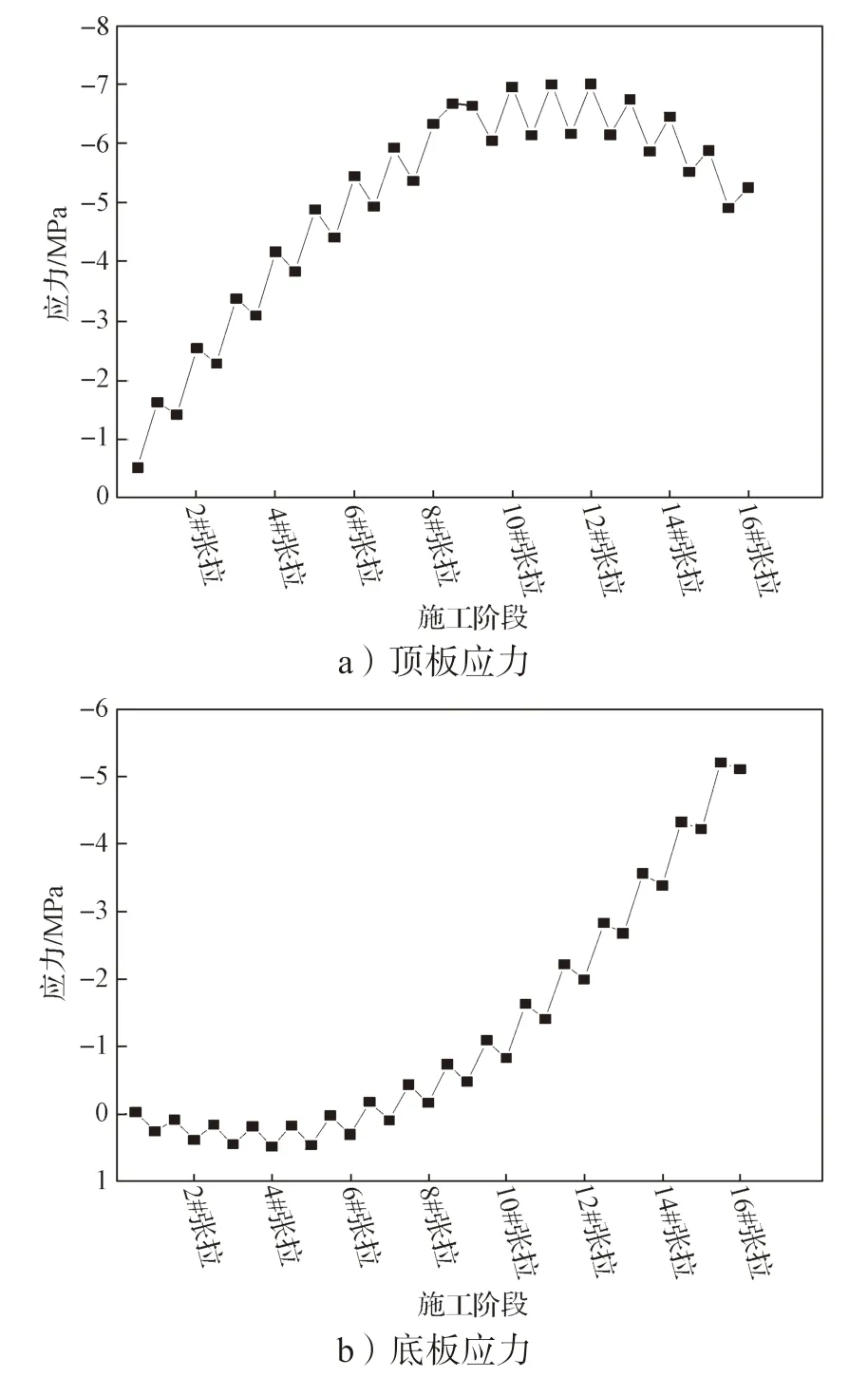
图8 3 号截面应力结果分析图Fig.8 Stress result analysis of section 3
由图8 可知,3 号截面箱梁顶板承受的应力多为压应力,在对称施工阶段中箱梁顶板应力会随着悬臂长度的增加而增大,进入非对称施工阶段后,箱梁顶板应力随着悬臂长度的增加而减小,箱梁顶板最大压应力为6.99 MPa;对比图7 和8,可知箱梁底板的应力变化规律与2 号截面底板的应力变化规律基本一致,箱梁底板的最大拉应力为0.477 MPa,最大压应力为5.2 MPa。
4 号截面位于2 号墩中跨1/2 处,包含对称施工阶段及非对称施工阶段,其应力分析结果见图9。
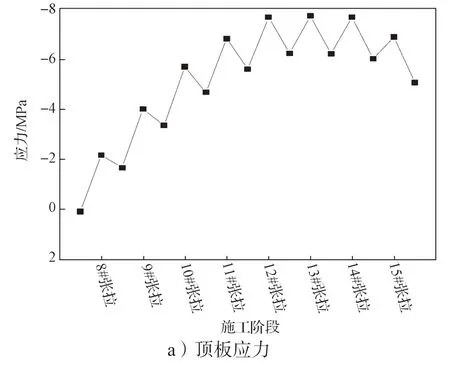
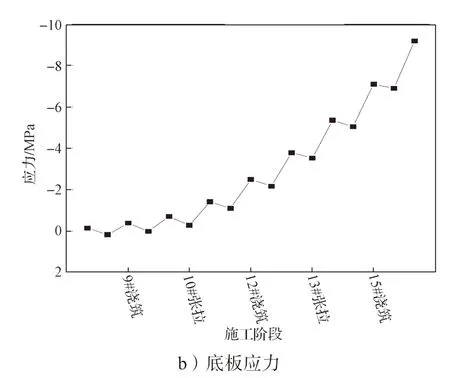
图9 4 号截面应力结果分析图Fig.9 Stress result analysis of section 4
观察图8 和图9 可以发现,4 号截面箱梁的顶板应力变化规律和3 号截面箱梁的顶板应力变化规律基本相同。由图9a 可以得知,箱梁顶板应力在对称施工阶段中,随着施工节段的增加而增大,而进入非对称施工阶段后,箱梁顶板应力开始减小,最大压应力为7.68 MPa。4 号截面位于中跨1/2 处,由图9b 可知,箱梁底板应力基本上都为压应力,并且可得知最大的压应力为9.18 MPa。
对比分析图7~9 可以得知,各截面箱梁顶板的压应力会随着下一梁段浇筑后减小,而在预应力钢束张拉后增大。箱梁底板应力的变化趋势与顶板应力的变化趋势相反;在对称施工阶段中,各截面箱梁顶板和底板的压应力均呈现出总体上升的变化趋势,在非对称施工阶段中,各截面箱梁顶板的压应力呈现出总体下降的变化趋势;本桥箱梁采用C55 混凝土进行浇筑,其混凝土抗压强度标准值和抗拉强度标准值分别为35.5 MPa 和1.96 MPa。在模型计算值中,3 个截面中最大的压应力为12.8 MPa,最大的拉应力为0.545 MPa,均在安全值范围之内,表明其有着良好的安全使用条件。
1 号截面(2 号墩边跨合拢段)、9 号截面(3 号墩边跨合拢段)、5 号截面(中跨合拢段)现场应力数据如表2 所示。

表2 合拢段截面应力数据分析表Table 2 Stress data analysis of closure section MPa
分析表2 中的数据可以得知,合拢段浇筑后,截面应力较小,这可能是由于合拢段截面较小,桥身自身质量较小,故浇筑后所产生的应力较小。合拢段截面应力在预应力筋张拉后,合拢段截面应力增大很多,2 号墩边跨合拢段截面应力在张拉后,应力增加了约134%,3 号墩边跨合拢段截面的应力在张拉后,应力约增加了135%,中跨合拢段截面应力约增加了352%。虽然3 个合拢段截面中的最大应力为5.56 MPa,但是张拉后截面应力增加了2~4 倍,合拢段施工是桥梁施工中的关键工序,因此在进行合拢段张拉时,需要重点注意合拢段截面的应力变化,以避免不利情况的出现。
通过分析仿真模型计算值可以得知,箱梁顶板应力在不同施工阶段均处于受压状态,而箱梁底板随着施工的进行会出现不同的受力状态,即底板应力随着施工的进行会由拉应力转换为压应力。这一结论与黄斌等[5]经过研究得出的“曲线连续刚构桥在施工过程全截面受压”的结论有些差异,该差异可能是因为桥型的不同,布置的预应力钢束不同所引起的;而此结论跟陈备备[6]得出的研究结论基本一致,但是本研究中桥箱梁底板应力在施工过程中产生的拉应力有所偏大,这可能是在模型计算过程中由于预应力损失所导致的。
为了能更好地了解混凝土浇筑、预应力张拉和箱梁应力的相关性,下面对混凝土浇筑后和预应力张拉后与应力随梁段增加的相关性进行分析,所得结果如图10~13 所示。
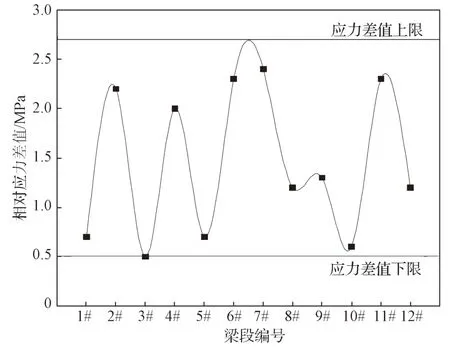
图10 2 号截面张拉后顶板相对应力值变化图Fig.10 Change diagram of the relative stress value of the roof after the tension of section 2
分析2 号截面顶板应力变化情况可以得知,前一梁段浇筑后至下一梁段浇筑张拉后的截面顶板应力会相对增加。从图10 可以看出,前一梁段浇筑后至下一梁段浇筑张拉后的截面顶板应力相对增加值随着梁段数的增加,即顺桥向梁段长度的增加,而呈现出在一定应力值范围的震荡变化规律,其震荡变化区间的上限值和下限值分别为2.60 MPa 和0.50 MPa。本桥1#梁段至5#梁段的长度为3 m,6#梁段至10#梁段的长度为4 m,从图中可以看出,混凝土浇筑后和预应力张拉后,其相对应力值与梁段长度呈现出一定的相关性。
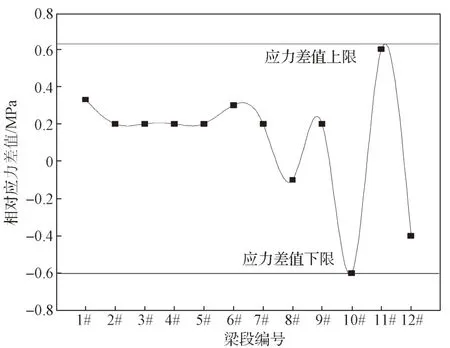
图11 2 号截面张拉后底板相对应力值变化图Fig.11 Change diagram of relative stress value of base plate after tension of section 2
分析2 号截面底板应力变化情况可以得知,在1#梁段至6#梁段施工阶段,2 号截面底板承受的应力为拉应力,在6#梁段至12#梁段施工阶段,2 号截面底板承受的应力为压应力,预应力张拉会引起箱梁底板拉应力增大。从图11 可以看出,在1#梁段至6#梁段施工阶段,前一梁段浇筑后至下一梁段浇筑张拉后的截面底板应力相对增加值随着梁段数的增加,即顺桥向梁段长度,呈现出平行趋势,在6#梁段至12#梁段施工阶段,前一梁段浇筑后至下一梁段浇筑张拉后的截面底板应力相对增加值随着梁段数的增加,即顺桥向梁段长度,呈现出在一定应力值范围的震荡变化规律,其震荡变化区间的上限值和下限值分别为0.62 MPa 和-0.60 MPa,由此可以得知,预应力张拉后对箱梁底板拉应力相对增加值随梁段数增加的相关性较小,箱梁的压应力相对增加值随梁段的增加相关性较大。
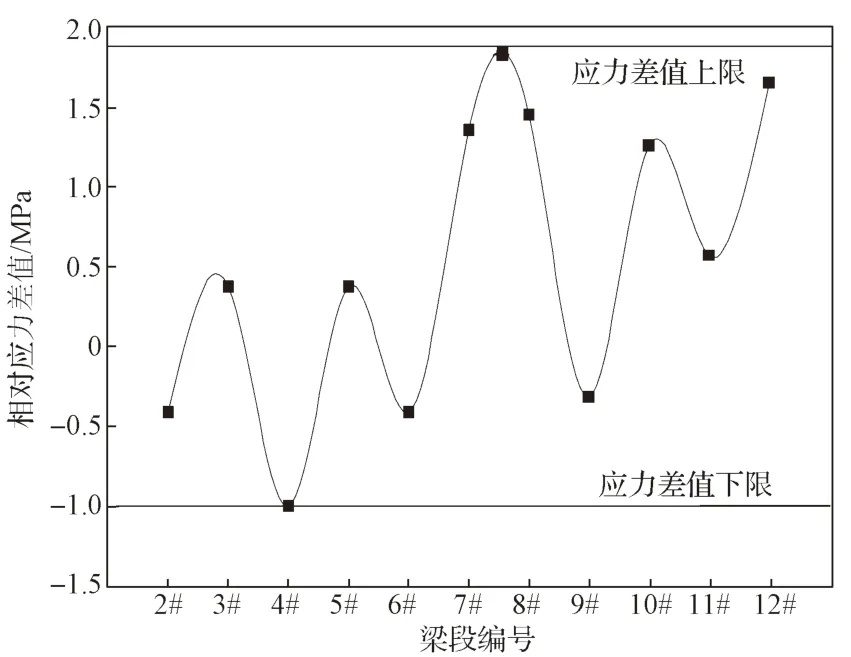
图12 2 号截面浇筑后顶板相对应力值变化图Fig.12 Change diagram of relative stress value of roof after pouring of section 2
分析2 号截面的顶板应力可以得知,前一梁段张拉后至下一梁段浇筑张拉后的截面顶板应力会相对增加。从图12 所示2 号截面浇筑后顶板相对应力值变化图中可以看出,前一梁段张拉后至下一梁段浇筑后张拉前的截面顶板应力相对减小值随梁段数的增加,即顺桥向梁段长度的增加,而呈现出在一定应力值范围的震荡上行变化规律,其震荡变化区间的上限值和下限值分别为1.9 MPa 和-1.0 MPa,且震荡上行幅度随梁段数的增加而增加。
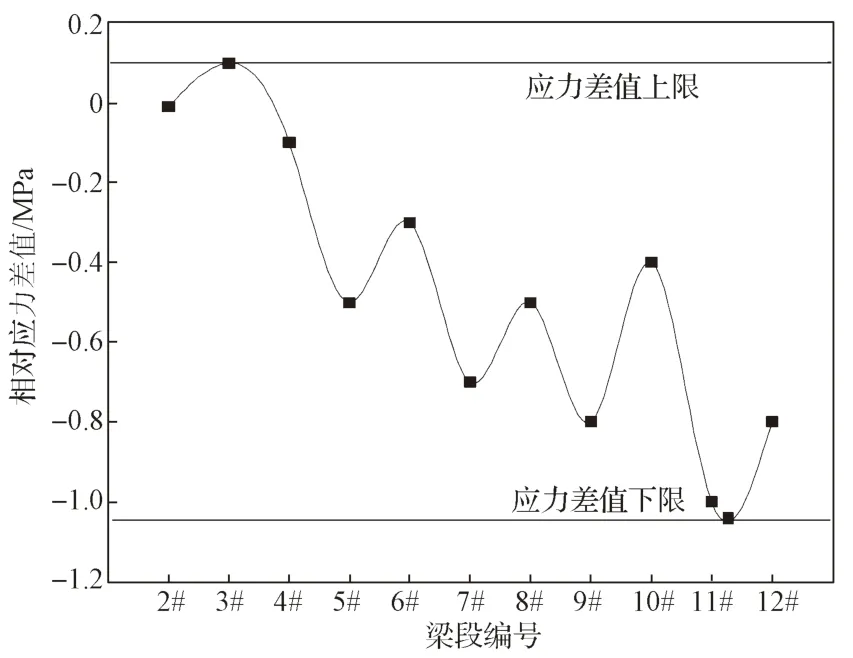
图13 2 号截面浇筑后底板相对应力值变化图Fig.13 Change diagram of relative stress value of base plate after pouring of section 2
分析2 号截面的底板应力变化可知,前一梁段张拉后至下一梁段浇筑后的截面底板应力会相对减小。从图13 所示2 号截面浇筑后的底板相对应力值变化图中可以看出,前一梁段张拉后至下一梁段浇筑后张拉前的截面底板应力相对减小值,随着梁段数的增加,即随着顺桥向梁段长度的增加,而呈现出在一定应力值范围的震荡下行变化规律,其震荡变化区间的上限值和下限值分别为0.10 MPa 和-1.02 MPa,且震荡下行幅度随着梁段数的增加而增加;本桥1#梁段至5#梁段的长度为3 m,6#梁段至10#梁段的长度为4 m,相对应力值与梁段长度呈现出一定的相关性。由此可以得知,浇筑后引起的箱梁顶板相对应力值随梁段数增加的变化规律与箱梁底板相对应力值随梁段数增加的规律完全相反。同时,箱梁承受的压应力和拉应力,在张拉后,相对应力减小值随梁段数的增加都有着一定的相关性。
4 结论
本研究通过对湖南省长沙市桐溪路景观桥在不同施工阶段的应力变化规律进行分析,可以得出如下结论:
1)在对称施工阶段中,箱梁顶板应力随着悬臂长度的增加而增长,在预应力钢筋张拉后,会引起箱梁顶板应力增大;箱梁底板会出现拉应力和压应力,随着施工的进行,箱梁底板会由拉应力转换为压应力,拉应力与压应力都随着悬臂长度的增加而增大。当进入到非对称施工阶段中,箱梁顶板应力随着悬臂长度的增加而减小,而箱梁底板应力会随着悬臂长度的增加而增大。
2)在对称施工阶段中,各截面箱梁顶板和底板的压应力呈现出总体上升的变化趋势,而在非对称施工阶段中,各截面箱梁顶板的压应力呈现出总体下降的变化趋势,箱梁底板应力变化规律与顶板应力变化规律相反。
3)合拢段在预应力钢束张拉完成后,截面应力约增加了2~4 倍,故在合拢段进行张拉时,应重点注意合拢段的截面应力变化情况,以避免不利情况的出现。
4)分析混凝土浇筑、预应力张拉时,箱梁应力随梁段数增加的相关性可知,前一梁段浇筑后至下一梁段浇筑张拉后的截面顶板压应力相对增加值随梁段数的增加呈现出在一定应力值范围的震荡变化规律;前一梁段张拉后至下一梁段浇筑后张拉前的截面顶板应力相对减小值,随着梁段数的增加,呈现出在一定应力值范围的震荡上行变化规律,截面底板应力相对减小值随梁段的增加呈现出在一定应力值范围的震荡下行变化规律。
