基于卷积神经网络的光伏逆变器故障诊断

陈旺斌，孟献蒙，程凡永, ，徐 杰,

（1.安徽工程大学 高端装备先进感知与智能控制教育部重点实验室，安徽 芜湖 241000；2.安徽工程大学 电气传动与控制安徽省重点实验室，安徽 芜湖 241000）

1 背景知识

随着工业化的快速发展，电子设备早期故障检测已成为一项必要技术，同时也是一项难点技术。近年来，随着人工智能的发展，越来越多的基于数据驱动的故障诊断技术被运用到设备故障诊断中，其中最典型的是深度学习中的卷积神经网络（convolutional neural network，CNN）模型[1]。文献[2]针对高速列车转向架故障问题提出一种利用一维CNN 提取高速列车故障信号深层特征模型，该模型能自动完成原始数据的特征提取和选择，进而实现对不同工况下转向架故障的分类。文献[3]提出一种基于二维CNN 的故障诊断方法。首先，设计了一种一维时间信号到二维图像信号的转换方法，在此基础上提出了基于二维图像信号的故障诊断算法，并在电机轴承数据集、自吸离心泵故障诊断数据集和轴向数据集上进行了训练和测试，实验结果显示，CNN 在基于数据驱动的故障诊断领域具有良好潜力。文献[4]针对轴承故障，利用CNN 对轴承信号故障数据进行特征提取和故障检测，实验结果表明，CNN 能可靠、有效地提取可分性强的故障特征，提高了系统故障诊断性能。

光伏逆变器是一种功率电子电路器件，其电路结构如图1 所示。光伏逆变器能将太阳能电池板的直流电压转换为交流电压，以驱动家用电器或者升压并入能源互联网。图1 中，绝缘栅双极型晶体管（insulated gate bipolar transistor，IGBT）是光伏逆变器的核心部件。当发生开路故障时，尽管系统还能继续运行，但有着很大的隐患，没有发生开路故障的IGBT 会流过较大电流，对整个电路系统产生影响，进而影响能源互联网的稳定运行。因此，及时准确地诊断开路故障对能源互联网的稳定运行具有重要意义。同时，使用逆变器输出电压或电流为特征量进行故障诊断时，需要3 个传感器进行三相电压或电流信号的检测，但以直流侧电流作为特征量时，则只需要1 个传感器。

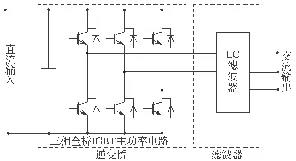
图1 逆变器的电路结构Fig.1 Inverter circuit structure

综合以上因素，本研究拟从减少传感器数目的角度出发，采用直流侧电流作为检测量，利用卷积神经网络实现对IGBT 开路故障的诊断。

2 光伏逆变器故障仿真

2.1 逆变系统仿真

实验利用Matlab 软件中的Simulink 仿真模块，搭建了一个光伏逆变器仿真模型，如图2 所示。

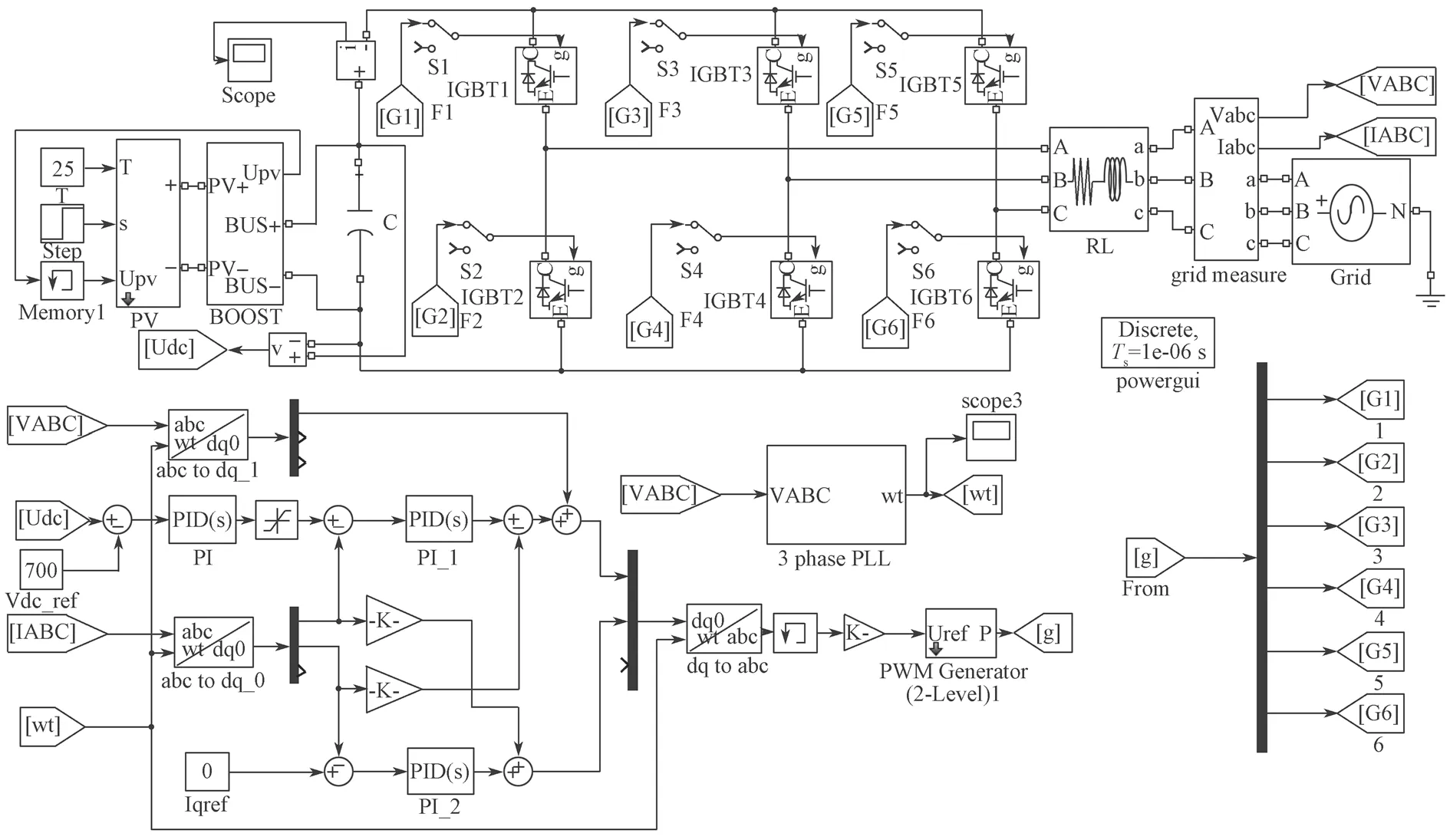
图2 光伏逆变器故障仿真图Fig.2 Photovoltaic inverter fault simulation diagram

实际光伏发电系统中，当光照强度发生变化时，其输入逆变系统中的电压会发生变化。仿真系统的光照强度在0.25 s 时由0.7 kW/m2突变为1.0 kW/m2，为抑制由此引起的电压波动，加入了相应的控制模块，以实现对输出电压的稳定控制[5]。

本研究的仿真电路图，主要由光伏与Boost 电路模块、逆变器、滤波电感、电压电流双闭环控制策略模块以及驱动信号模块5 部分组成。该系统可以有效地在光照强度发生变化时快速地将输出电压调节到所需电压，保证系统的稳定性[6]。运用这个仿真系统来模拟真实电路中的IGBT 开路故障，选择的做法是添加开关来控制激励信号，当某个开关断开时，相应的桥臂就不会收到触发脉冲，这样该桥臂的IGBT 就不会导通，就相当于IGBT 管开路。在三相桥式逆变电路中有6 个IGBT 管（每个IGBT 反并联1 个二极管），每个IGBT 管都是有可能发生故障的，但是发生故障时，1 个或者2 个IGBT 管故障的概率极高，很少有3 个或3 个以上IGBT 管同时发生故障[7]，所以本文中只分析IGBT 管1 个或者2 个发生开路时的情形。根据三相桥式逆变电路的构造，共有6 种单管故障情形。当有2 个管子发生故障时：1）同一相两个桥臂同时发生故障；2）上桥中两个桥臂同时发生故障；3）下桥中两个桥臂同时发生故障；4）上下桥臂交叉的同时发生故障，总计有15 种故障。因此，加上正常状态，总计有22 种状态类别。

2.2 数据采集

每个故障在实验中的持续时间均为4.1 s，而前0.1 s系统刚刚通电，数据的波动巨大，所以舍去这一部分数据，故数据采集的时间为0.1～4.1 s。在正常工作状态下，输出电压频率为50 Hz，也就是0.02 s 为一个周期。通过设计的仿真模型采集正常工作和各种不同故障下的直流侧电流数据，用作实验的训练和测试数据。所得的仿真电流图显示，虽然不同故障的运行时间相同，但获得的直流侧电流数据数量是不一样的。为了保证输入数据的维度一致性，需要对电流进行等时间采样，采样频率为10 000 Hz，这样可以保证数据的维度一致。且为了能更好地提取数据特征，需要加大数据集，同时输入网络的数据维度大小对于神经网络训练也非常重要。因此，在数据输入网络模型之前对数据进行了预处理——数据移动。数据检测步长的大小需要通过实验来确定一个最佳值，检测步长代表两次检测的时间差，在采样频率固定的情况下，就代表两次检测的样本移动长度。数据移动后，样本集的数量会增加。例如，实验中采用了一种如图3所示的移动方法。

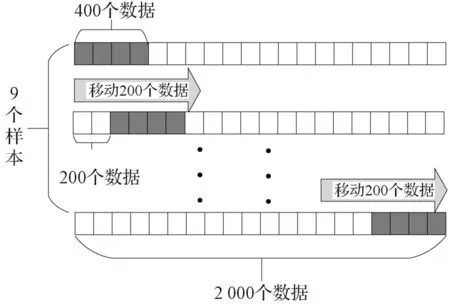
图3 数据移动示意图Fig.3 Schematic diagram of data movement

由图3 可知，一段原始采样样本总共有2 000个数据，首先将其前400 个数据划为一个数据片段（1～400 个采样数据），之后以步长为200 向右移动，对数据进行划分得到第二个数据片段（201～600 个采样数据）。按照这种移动方法，最后就可以将原始的长度为2 000 的数据，划分为9 个长度为400 的数据片段。总共采集了352 段训练数据样本，最后可以得到3 168（352×9）条训练数据片段。对测试样本也采取相同的处理方法，总共采集了88 条训练数据片段，这样移动后就得到792（9×88）条测试数据片段。

从仿真模型中采集而来的数据不存在噪声，为模拟实际的噪声情况，后续处理中对数据都加入了不同信噪比的噪声，通过观察数据集可以发现，数据的最大最小值相差很大，为了提高模型的收敛速度，对数据进行了标准化预处理。标准化处理的目的是将数据按比例缩放，使之落入一个小的特定区间，则标准化公式如下：

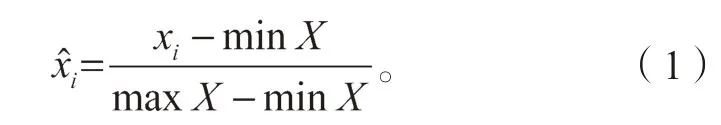
3 一维卷积神经网络

3.1 卷积层

卷积神经网络是一种应用广泛的前馈神经网络，已在很多领域中成功应用[8]。通常情况下，卷积神经网络包括输入层、卷积层、池化层、全连接层和输出层[9]。数据进入卷积神经网络后，首先进入卷积层进行卷积运算，也就是卷积核与输入数据进行局部加权求和[10]。在实际运用中，往往是由多个输入特征图和多个卷积核组成，为方便理解，以图4 展示一个输入特征图和一个卷积核时的运算。在卷积运算结束后，加上偏置项后选用ReLU 激活函数提升卷积神经网络的表达能力和抑制梯度消失现象[11]。

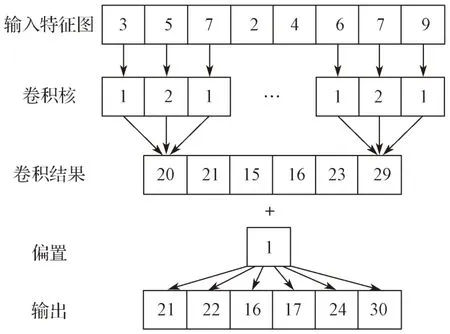
图4 一维卷积运算过程示例Fig.4 Illustration of one-dimensional convolution operation process

在卷积层中，每一个输出特征图都是由多个输入特征图组合的卷积结果，例如，第l-1 层的特征图经过卷积和激活后输出第l 层的特征图，其前向传播公式为

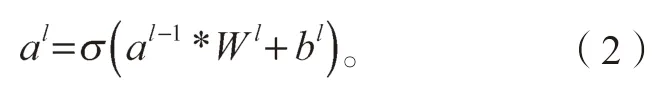
式中：al-1是第l-1 层的输出特征图的集合，同时是第l 层的输入特征图的集合；

al为第l 层的输出特征图的集合；

Wl为第l-1 层到第l 层卷积核的集合；

bl为第l-1 层到第l 层的偏置项；

*表示卷积作用；

σ( · )为激活函数。

推导可得卷积层的反向传播公式如下：

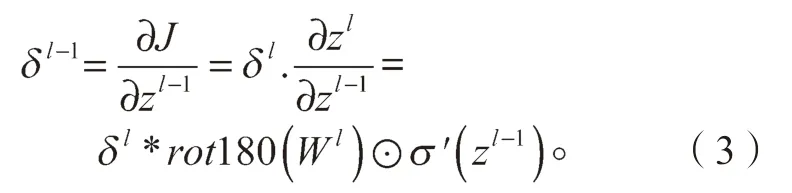
式中：zl为第l 层的卷积结果，且

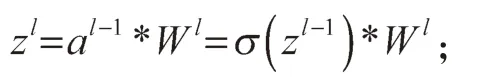
δl-1为第l-1 层的梯度；

δl为第l 层的梯度；

rot180(·)表示将核旋转180 度；

3.2 池化层

在卷积神经网路中，池化层的作用是将卷积层输出的特征图缩小，有最大池化、最小池化、平均池化、随机池化等[12]。图5 列出了最大池化和平均池化的运算结果，通常最大池化可以有效地提取特征，比较适用于分类问题。本文模型中采用了最大池化，从目标区域中取出最大值，通过池化层的二次提取特征进行降维，进一步降低网络的计算量。经过多次的卷积和池化运算后，即可获得数据特征，最后连接到全连接层进行分类[13]。

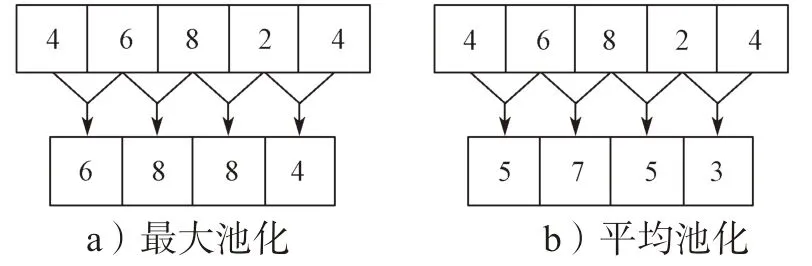
图5 一维池化运算示例Fig.5 Illustration of one-dimensional pooling operation

从l 层到第l+1 层的池化前向传播公式如下：

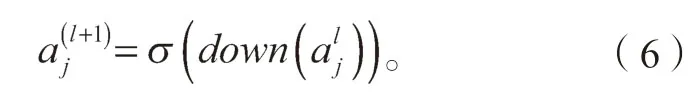
式中，down(·)是一个下采样方法，池化层窗口大小为n×1，则对池化层窗口滑过的每一个n×1 块中的元素进行相对应的池化运算，得到一个1×1 的输出特征图，缩小为原来的1/n。

根据反向传播方法，可推得池化层的反向传播公式为

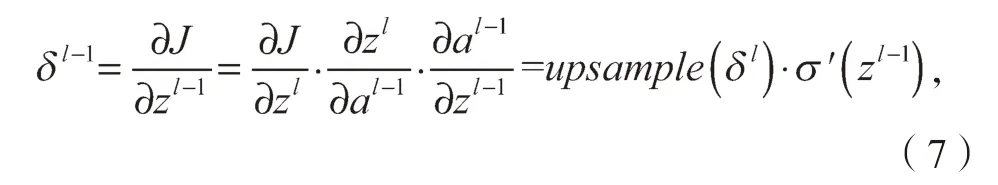
式中，upsample(δl)表示上采样操作，即将每个元素在一个维度上展开n 次，还原到池化之前的大小，n为down(·)下采样时缩小的比例。

CNN 在池化层反向传播时如图6 所示，对于池化层的梯度δl，首先还原为池化前的长度，然后根据池化类型进行数值分配，如果采用的是最大池化，就需要将δl中的数值分配到池化前的最大位置处，如果采用的是平均池化，就将δl等分为n 份再分配到各个位置处。

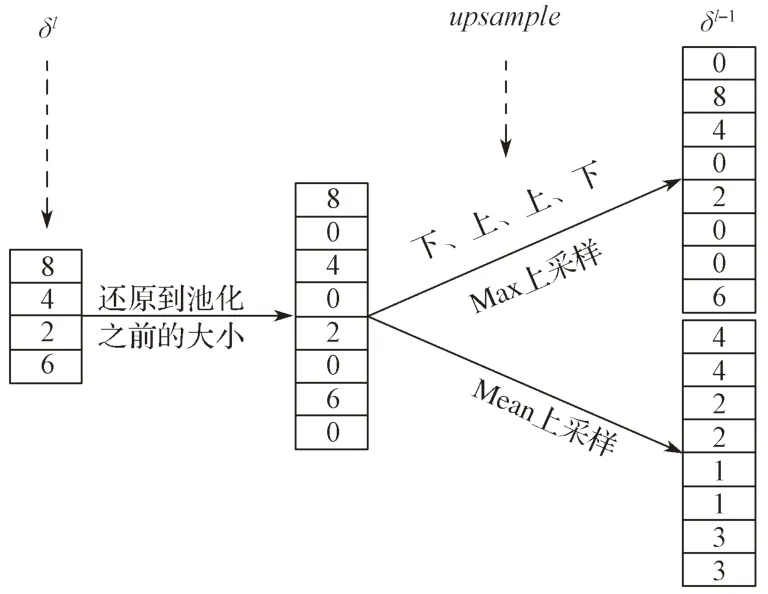
图6 池化层的反向传播示例Fig.6 Illustration of back-propagation in the pooling layer

通过上述卷积层和池化层的反向传播，可以求得参数的梯度，这样就可以利用梯度下降法来更新所构建的卷积神经网络中所有的参数，最后得到一个能实际运用的模型。

4 实验结果和分析

4.1 检测步长

为验证所提方案的可靠性，将本文模型与支持向量机（support vector machines，SVM）和k 最近邻（k-Nearest Neighbor，kNN）分类算法进行比较。

1）SVM 故障诊断方法。采用与CNN 模型相同的数据集，选用线性核函数，运用间接法的多分类器进行故障诊断。

2）kNN 故障诊断方法。kNN 通过测量不同特征值之间的距离进行分类。如果一个样本在特征空间中的k 个最邻近的样本中的大多数属于某一个类别，则该样本也被划分为这个类别。在kNN 的参数设置中，k = 9。

为了确定最佳检测数据步长，课题组采用了信噪比为10 dB 的数据进行训练与测试。逆变器正常工作时，输出的三相电压频率为50 Hz，直流侧电流的采样频率为10 000 Hz，因此在输出电压的一个周期（0.02 s）时间内，可以采集到200 个电流值。为此，以200 为中心，分别将数据检测步长100, 150, 200,250, 300 输入到已经搭建好的网络模型（CNN 参数设置如表1 所示）中进行训练与测试，得到如图7 所示的3 种方法下不同检测步长对应的测试结果图。

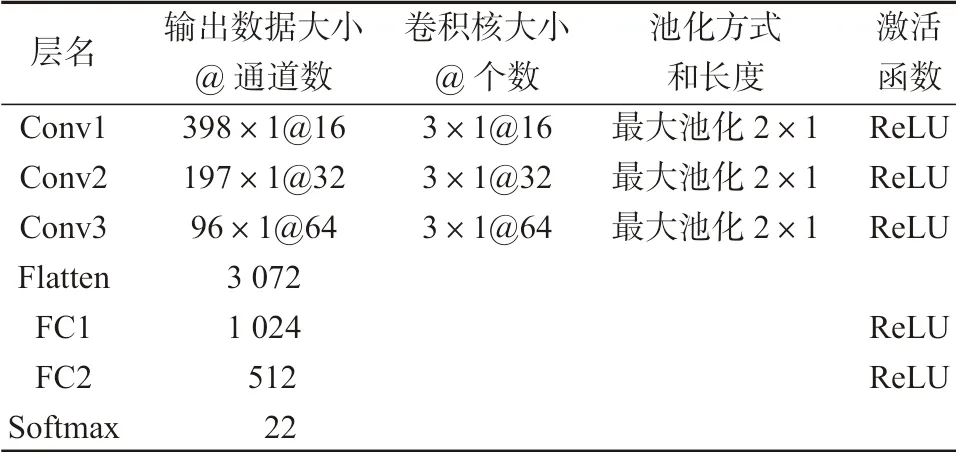
表1 CNN 网络参数Table 1 CNN network parameters

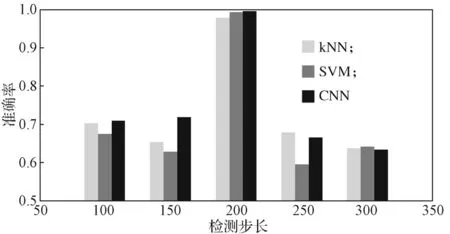
图7 不同检测步长下3 种方法的准确率比较Fig.7 Accuracy comparison of three methods under different moving steps

由图7 可以看出，不同的检测步长对最后的测试准确率有一定的影响，当检测步长为100，150，250，300 时，得到的结果都不理想，当检测步长为200 时，得到的检测效果最佳。因此，本文后续实验中将步长200 设置为默认检测步长。当检测步长为200 时，可以得到3 168 条训练数据，每条包含400个样本点。将数据进行标准化后输入CNN 模型中，经过相应的卷积和池化后，将数据串联并传入全连接层，此外为防止过拟合对全连接层使用了Dropout[14]技术，最后接SoftMax 函数输出，得到该条数据所对应的故障类别概率分布。

4.2 对比结果

为了验证CNN 模型的实用性，分别将信噪比为5,1, 0, -1 dB 的数据放入网络中进行训练和测试，所得实验结果如图8 所示。

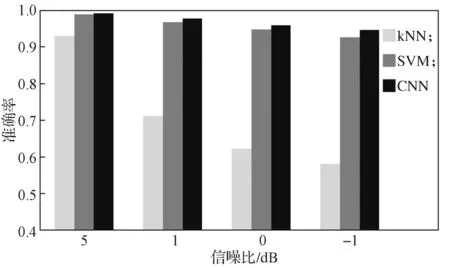
图8 不同信噪比下3 种方法的准确率比较Fig.8 Accuracy comparison of three methods under different SNR

由图8 可以得知，kNN 在低信噪比故障数据分类中的准确率最低，这说明kNN 方法的噪声鲁棒性比较弱。与kNN 相比，SVM 和CNN 的分类准确率均有显著的提升，其中CNN 在三者中的准确率最高，5, 1, 0, -1 dB 信噪比下的准确率分别是0.992 4, 0.978 5,0.959 6, 0.945 9。这一结果说明，在逆变器开路故障诊断性能上，CNN 相对其他的算法效果更好。

5 结语

本文以光伏逆变器的直流侧电流为研究对象，提出了一种基于CNN 的光伏逆变器故障诊断新方法。实验结果表明，在CNN 网络结构中，数据的检测步长为200 时，故障诊断效果最佳。另外，为了测试该实验方法的鲁棒性和适用性，将5, 1, 0, -1 dB 的高斯白噪声人工添加到数据集中。得到的实验结果表明，该方法在不同噪声水平下仍然能获得高于94%的故障诊断准确率。

在后续研究中，准备搭建一个基于Dspace 的逆变电路模型，获取实际模型的故障数据，利用仿真模型和实际模型开展迁移学习方面的研究。