泵作透平定常流动数值计算

2021-01-13曾凡康周枫林杨加兵张玉良

湖南工业大学学报 2021年1期

孙晓，曾凡康，周枫林，杨加兵，张玉良

（1.湖南工业大学机械工程学院，湖南株洲 412007；2.衢州学院机械工程学院，浙江衢州 324000）

1 研究背景

近年来，随着能源短缺加剧和国家对二次能源开发的日益重视，泵作透平作为一种新型的能量回收利用设备，具有体积小、无污染、便于使用等特点。采用泵作透平进行高压能量回收再利用是节能环保的一个重要研究方向。离心泵在作透平的过程中其内流特性相较泵会发生较大的变化，因此有必要对泵及泵作透平的内流结构和特性进行研究。

国外学者S.Derakhshan 等[1]对4 台低比转速的离心泵进行了反转实验，推导预测出了泵与透平最佳效率点的关系式，提出了一种小型水泵的选型方法。Morros C.Santolaria 等[2]选取一台单级单吸蜗壳式离心泵为研究对象，根据计算结果得到泵反转作液力透平时的内部流场分布。S.V.Jain 等[3]针对叶轮进口直径、叶片进口边修圆与转速对透平性能的影响进行了试验研究，通过回归分析，给出了透平高效点参数预测的经验系数表达式，进一步将预测精度提高到了10%以内。J.Fernández 等[4]通过实验对比了不同转速下离心泵的性能参数，并通过实验数据和计算数值对比分析得到了根据泵推测透平性能曲线的方法。E.Frosina 等[5]选取3 台不同比转速的工业离心泵为研究对象，利用CFD（computational fluid dynamics）技术对离心泵反转作透平进行了数值计算，并对透平的外特性进行了评估。

国内学者Yang S.S.等[6-7]总结了泵作透平的相关理论，分析了泵作透平的外特性，建立了离心泵全流道的简化模型，使用CFD 技术对网格类型和湍流模型进行了研究。并对泵作透平的性能进行了数值计算，提出了一种较为准确预测泵作透平的经验公式。杨军虎等[8-9]对3 个比转速不同的泵作透平进行了数值计算，拟合出离心泵反转工况时的性能预测计算式，并对一台中比转速的离心泵反转的力学特性进行了研究，验证了数值计算方法对离心泵的性能分析的可靠性。袁亚飞[10]采用统计的方法，对4 台低比转速离心泵的数值试验结果进行了分析，得到了泵的外特性与反转作为能量回收透平时的外特性之间的关系。黄思等[11]通过CFD 软件对单级离心泵进行了全三维流场的常态、瞬态模拟计算，并研究了叶轮内部流道的流固耦合、空化等内部特性。史广泰等[12]通过改变一台离心泵的导叶数及进口截面面积，对其内部流场进行了对比计算，得到了透平蜗壳与叶轮内压力脉动情况。王晓晖等[13]采用数值计算模拟了泵与透平在工况下的速度滑移特性，揭示了滑移系数的变化规律，提出了一个考虑滑移系数时计算泵工况与透平工况扬程换算关系的新方法。

以上研究均采用CFD 技术对离心泵作透平相关特性进行了探究，减少了实验所需特定环境的时间和成本。同时，对比实验数据可验证数值计算正确性和可靠性。本文以一台低比转速的离心泵为例，建立了离心泵的简化模型，使用ANSYS-CFX 流体仿真软件对不同工况下的离心泵进行模拟计算，得到泵及透平流场的外特性，同时在后处理中可获得该透平泵的内流特性，并将最优工况下的泵和泵作透平进行对比分析。

2 模型参数

本研究中离心泵的额定参数如下：流量Q=25 m3/h，扬程H=12.5 m，转速n=1 450 r/min。该离心泵作液力透平的主要几何参数见表1。

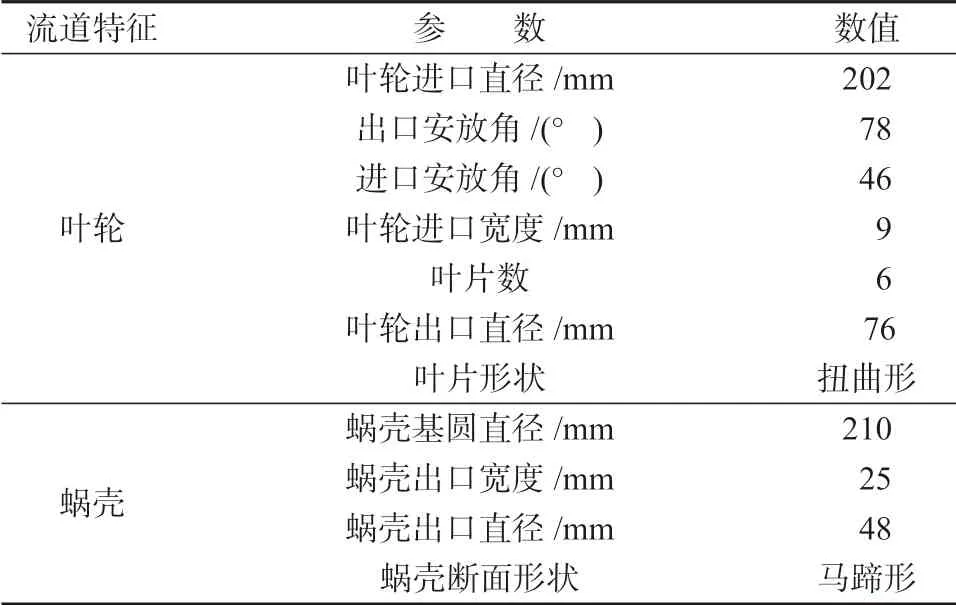
表1 模型主要几何参数Table 1 Main geometric parameters of the model

3 数值模拟方法

3.1 网格生成

为研究泵内流体复杂的三维流动结构及全过程的压力、速度等变化特性，本文采用ANSYS ICEM对离心泵进行六面体网格划分，透平模式下网格划分如图1 所示。

图1 网格模型Fig.1 Grid model

将划分之后的网格从90×104到165×104不同的网格数量进行网格无关性验证，结果如图2 所示。

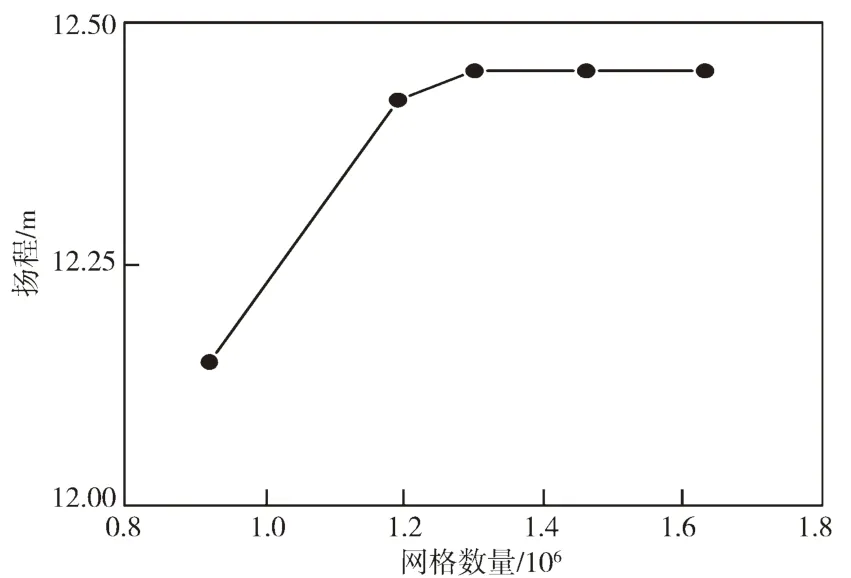
图2 网格无关性验证Fig.2 Grid independence verification

由图2 可以看出，当网格数量为120×104以上时，泵的扬程变化在0.5%的范围内，此后网格数量继续增加对泵的扬程计算变化不敏感，因此选择数量在120×104以上的网格比较合适，并在叶片表面和蜗舌处进行网格加密处理。整个计算域网格数量总数为1 194 160，其中叶轮网格数量为480 612，蜗壳网格数量为455 152。

3.2 边界条件

采用ANSYS-CFX 软件进行定常计算。进口边界条件设置为恒压进口，出口边界条件设置为质量流量。通过改变出口流量来获得泵及泵作透平的外特性曲线。设置收敛精度为10-5，叶轮表面和其他壁面均无滑移，在近壁低雷诺数区域采用标准壁面函数法处理高雷诺数湍流模型带来的问题，输送介质为常温清水。为了计算过程的稳定性，将入口管道延长至进口直径的2 倍，出口管道延长至出口直径的5 倍[14]。选用SIMPLEC 算法及k-ε 湍流模型进行相应的计算，过流部件动静结合部位被设置为interface 连接。

4 计算结果与分析

4.1 外特性

图3 所示为计算得到的泵及泵作透平的外特性曲线。可见，透平的最高效率为78.1%，其对应的流量为32.5 m3/h，扬程为21 m，轴功率为1.86 kW。

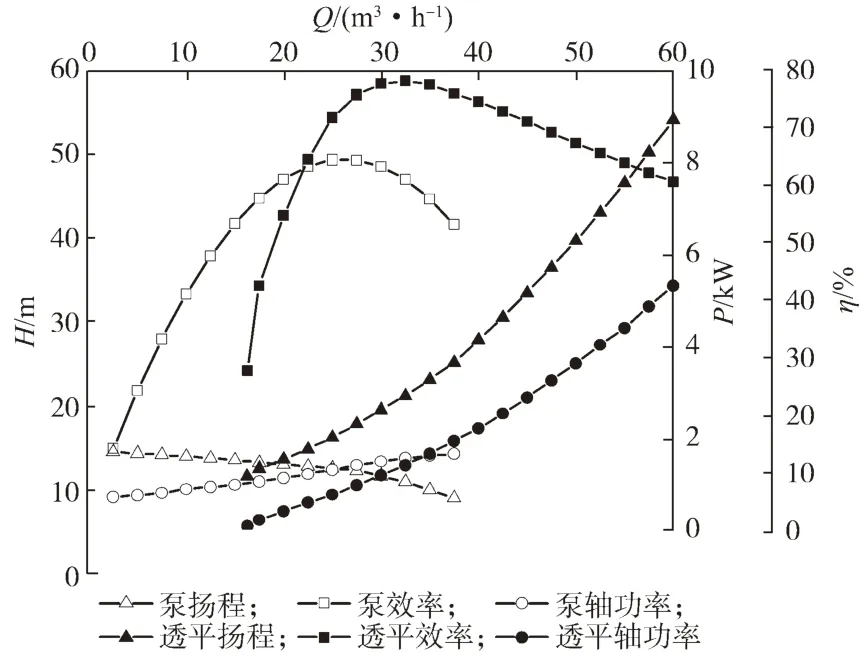
图3 泵及泵作透平外特性曲线Fig.3 External characteristics curves of the pump and pump as the turbine

泵的效率和透平效率都存在一个峰值。泵的最高效率点在设计工况点，其效率为62.5%。流量在0.7Qp～1.3Qp（Qp为泵额定工况流量）之间，效率相对于最高点变化了1.5%～6.5%；流量在0.5Qp～0.7Qp之间，效率相对于最高点变化了6.5%～22.7%；流量在1.3Qp～1.5Qp之间，效率相对于最高点变化了6.5%～14.9%。可见，低流量工况下和高流量工况下效率变化幅度较大。该泵作透平的最高效率为78.1%，其流量在0.7Qt～ 1.3Qt（Qt为透平最优工况流量）之间，效率相对于最高点变化了6.4%～10.9%；流量在0.5Qt～0.7Qt之间，效率相对于最高点变化了10.9%～68.3%；流量在1.3Qt～1.5Qt之间，效率相对于最高点变化了6.4%～12.3%；流量在1.5Qt～1.7Qt之间，效率相对于最高点变化了12.3%～18.4%。可见，透平在其低流量工况下的效率变化幅度较大，与泵不同的是，透平在高流量工况下效率变化幅度较缓，说明透平在高流量工况下高效区宽阔。透平的最大效率值是泵最大效率值的1.25 倍。

泵的扬程随着流量增大而逐渐减小。流量在0.3Qp～1.5Qp范围内，泵扬程减少了5.4 m。流量在0.7Qp时扬程为13.28 m，该点处扬程的减少率（单位变化流量的扬程减少量）为0.107，流量在Qp时扬程为12.37 m，该点处扬程的减少率为0.112，在1.3Qp时扬程为11.09 m，该点处扬程的减少率为0.327。可见，泵的扬程随着流量变化减少幅度增大。与泵不同的是，透平扬程随流量增加而增加。流量为0.5Qt～1.5Qt范围内，透平扬程增加了27.2 m。流量为0.7Qt时的扬程为14.94 m，该点处扬程的增加率（单位变化流量的扬程增加量）为0.53。流量为Qt时的扬程为21.02 m，该点处的扬程增加率为0.72。流量为1.3Qt时的扬程为30.52 m，该点处的扬程增加率为1.1。可见，透平扬程随着流量增加增长率变大。泵和透平在各自最优工况点时，透平扬程是泵扬程的1.7 倍。

泵与透平的功率随着流量增大而逐渐增大。流量为0.5Qp～1.5Qp，泵功率增加了0.72 kW；流量为0.5Qt～1.5Qt，透平功率增加了3.43 kW，可见透平的功率随流量增加增幅比泵大。当流量低于35 m3/h 时，泵的功率比透平的功率大；流量为35 m3/h 时，泵与透平的功率基本相等。在流量为Qp时，泵的功率为1.35 kW，该点处的功率增长率（单位变化流量的功率的增加量）为0.04。在流量为Qt时，透平的功率为1.44 kW，此时的功率增长率为0.09。在流量为1.3Qp时，泵的功率为1.59 kW，该点处的功率增长率为0.025。在流量为1.3Qt时，透平的功率为2.56 kW，该点处功率增长率为0.13。流量为1.5Qp时，泵的功率为1.68 kW，该点处功率增长率为0.016。流量为1.5Qt时功率为3.45 kW，该点处功率增长率为0.15。可见，随着流量继续增大，透平功率的增长速度比泵要快，且增长率也不断增加。泵和透平在各自最优工况点时，透平功率是泵功率的1.07 倍。

综上所述，透平的最高效率大于泵的最高效率。在各自最优工况点处，透平的最大效率值是泵最大效率值的1.25 倍。透平扬程是泵扬程的1.7 倍，透平功率是泵功率的1.07 倍。可见，该离心泵反转用作透平，对其扬程影响最大。

4.2 内流场特性

泵的进口（透平出口）压力设置初值为101 325 Pa，透平的进口压力初值设为303 975 Pa，分别计算出泵与透平的压力、速度、流线等相关参数变化。

1）压力场分布

图4 是泵与透平在最优工况下，中间平面的流场压力分布情况。从图中可看出，泵及透平内部流场压力分层明显。泵的静压从蜗舌到出口处分为2 层，压力变化范围为160～220 kPa，透平从入口到蜗舌处的静压分为4 层，压力变化范围为200～280 kPa，由此可见，从蜗舌到透平出口静压变化比泵要大。泵贴近蜗舌处的静压急剧增大，约为240 kPa。透平的静压在此处变化相对较小，约为200 kPa。该处压力变化与蜗舌所处位置及形状有关，在蜗舌处管道直径变小且形状不规则，造成了局部压力变大。从图中可以看出，泵的压力在泵叶轮进口（透平叶轮出口）处的相对压力较小，透平的低压区分布更广。沿叶片向外伸展，静压不断增大，泵和透平的静压变化范围在80～220 kPa。靠近泵叶轮进口处，流体受到叶片制约，压力分布沿着进口半径方向展开。

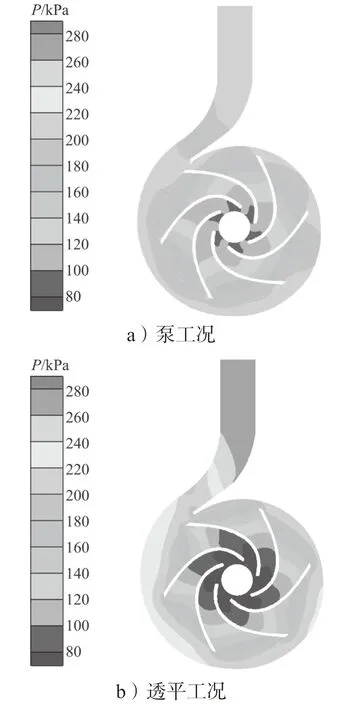
图4 泵与透平中间平面的流场静压分布Fig.4 Static pressure distribution of flow field in the middle surface between pump and turbine

为进一步探究泵和透平在工作过程中的能量变化过程，将计算域划分为如图5 所示的几个部分进行分析。

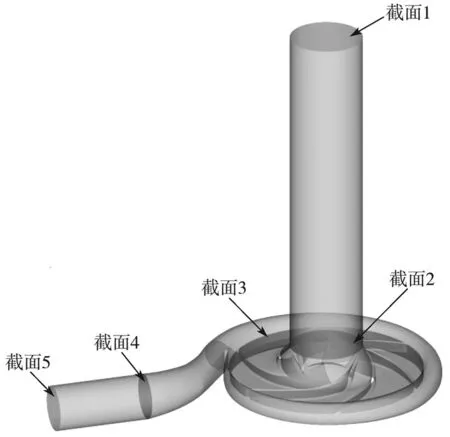
图5 各截面位置示意图Fig.5 Position diagram of individual section

各截面的总压力如图6 所示。在泵和透平的内部流道内，能量不断发生变化。泵出口处的压力值为15.20 kPa，泵进口处设置的压力值为101.331 kPa，其中，泵出口段产生的压力损失为1.92 kPa，蜗壳段产生的压力损失为19.25 kPa，进口段产生的压力损失为0.19 kPa，而泵在叶轮区域获得的压力约为150 kPa。蜗壳段产生了较大的水力损失，包括涡流损失、沿程损失、圆盘损失等。透平内部流道压力不断减小，透平进口段压力损失为0.30 kPa，蜗壳段损失约为13.75 kPa, 叶轮区域压力减少了139.80 kPa，出口段压力损失为3.36 kPa。由此可见，管道内壁、动静干涉以及其他因素对内部流场产生了一定的压力损失。其中，泵在蜗壳内产生了较大的水力损失。在叶轮区域，叶轮与水的相互作用产生了较大的能量转换。

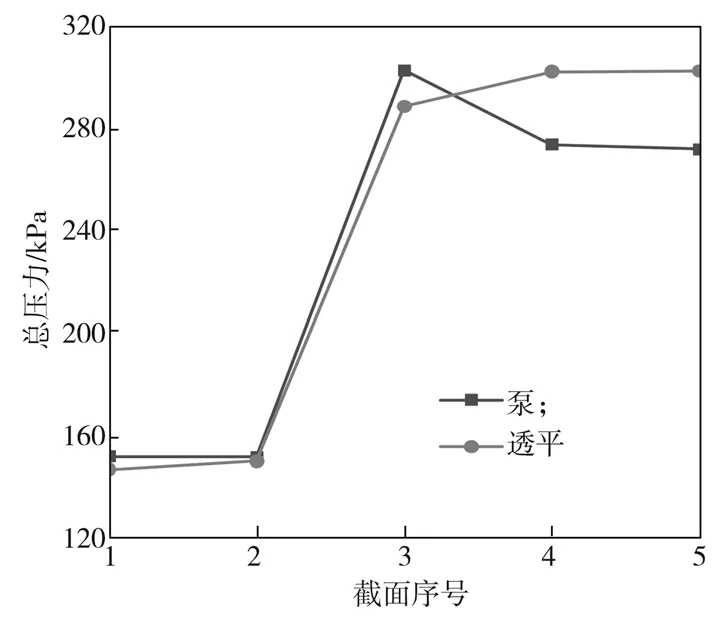
图6 各截面总压力Fig.6 Total pressure of individual section

为了直观地看到叶轮区域的能量变化，将叶片从叶轮计算域内提取出来，其静压分布如图7 所示。

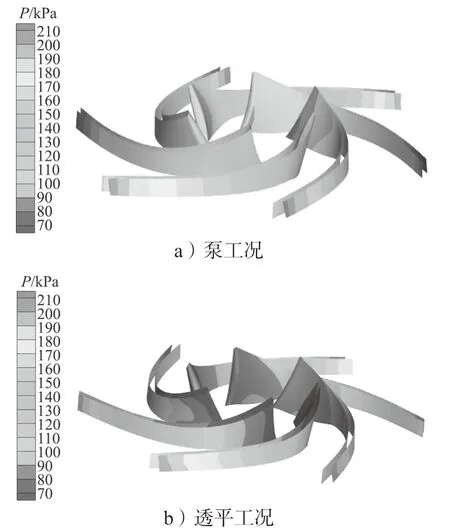
图7 不同工况的叶片静压分布云图Fig.7 Blade static pressure distribution under different working conditions

由图7 可知，沿着叶片伸展方向，叶片的压力变化量逐渐增大。

图8 为叶片部分的应变速率分布图。

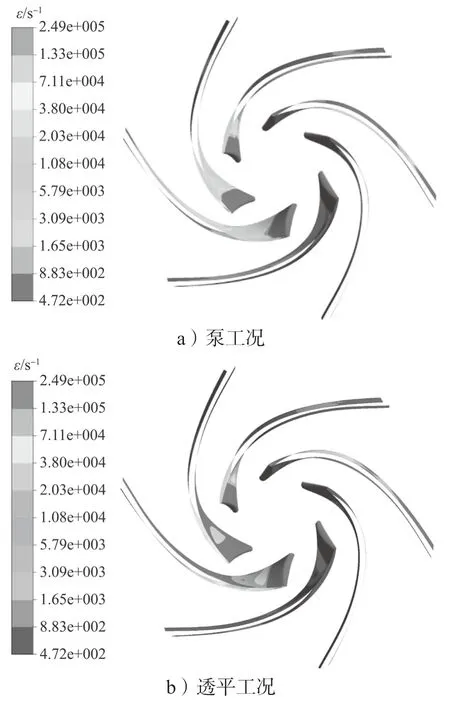
图8 不同工况的叶片应变速率分布云图Fig.8 Blade strain rate distribution under different working conditions

图8a 和图8b 上叶片的平均应变速率分别为19 327.1, 43 928.8 s-1。从图中可以看出，各叶片上的应变速率分布较为均匀，不同叶片间差别不大。透平叶片靠近蜗舌处的两个叶片应变速率较大，其余叶片相对较小。泵与透平叶片工作面应变速率比背面要大，叶片上应变速率最小处位于背面并靠近进口（透平出口）处，其大小分别为472, 883.4 s-1。在叶片工作面上，泵的应变速率沿叶片伸展方向呈现先减小后增大的趋势，叶片中部的应变速率值最小。在叶片相对长度为0～0.3的范围内，其大小为2.03×104～7.11×104s-1。透平的应变速率沿叶片伸展方向（与泵反向）大都呈现逐渐增大的趋势，远离蜗舌的叶片具有与泵叶片相似的规律。在叶片相对长度为0.7～1.0 的范围内，其大小在每个叶片上分布差异较大。靠近蜗舌的两个叶片上，应变速率为1.33×105～2.49×105s-1。远离蜗舌叶片上，应变速率为7.11×105～1.33×105s-1。在叶片背面，泵的应变速率沿叶片伸展方向呈现出先增大后减小的变化趋势，相对叶片长度为0.2～0.4 范围内的应变速率值最大，其大小为7.11×105s-1。透平背面的应变速率与泵的变化规律相同。在相对叶片长度在0.6～0.8 范围内的应变速率值最大，其大小为1.33×105s-1。

取6 个叶片的中截面进行分析，如图9 所示。理论上讲，液力透平的内部流道是轴对称的，由于受到蜗舌等因素的影响，使得叶轮内部流动并不是完全的轴对称，不同叶片上的压力和载荷会有所不同。叶片上的压力分层明显。

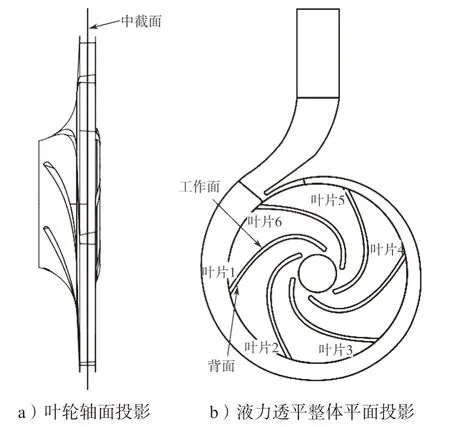
图9 液力透平叶轮及整体投影云图Fig.9 Hydraulic turbine impeller with its overall projection

如图10 所示为各个叶片在最优工况下工作面及背面的静压系数[15]分布曲线。其中，静压系数Cp的表达式为

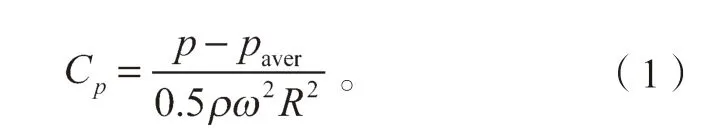
式（1）中：p 为叶片中截面上某点的静压；

paver为叶片中截面上的平均静压；

ρ 为流体的密度；

ω 为叶片旋转角速度；

R 为叶片上某点距中心处的距离。

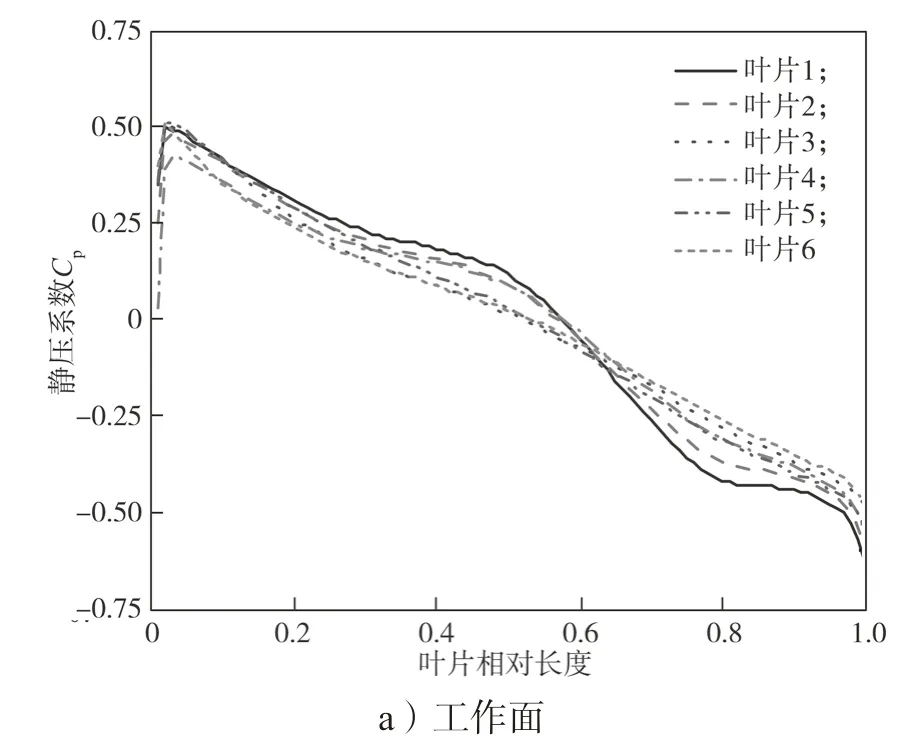
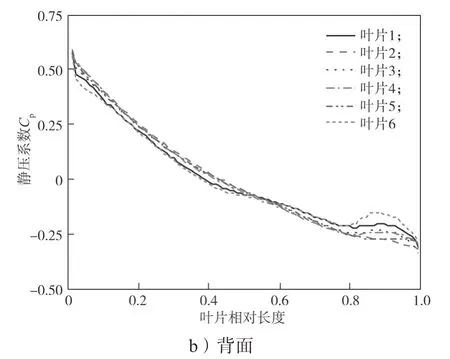
图10 最优工况下透平叶片静压系数分布图Fig.10 Static pressure coefficient distribution of turbine blade under optimal conditions

对比图10 中各个叶片的静压系数值发现，各个叶片上相对应位置的数值相差不多且分布规律相似，说明透平叶轮内部沿叶片伸展方向波动不大。从图10a 中可以看出，在透平叶片进口（泵叶片尾缘）处叶片静压突然增大，这是流体动静压变换的结果。其中，叶片1～6 的工作面静压系数最大值分别为0.50, 0.48, 0.50, 0.42, 0.51, 0.51，最小值分别为-0.63,-0.59, -0.48, -0.55, -0.54, -0.48。可见，各叶片工作面增加的静压系数值在0.5 左右。其中叶片5、6 的工作面静压系数值最大，叶片上随着相对长度增加其工作面和背面的静压系数逐渐减小。在相对长度小于0.5 时，叶片工作面上的压力系数均为正值。在相对长度为0.1～0.5 时，叶片6 的工作面静压系数最低，可见，在相对长度为0～0.1 之间时，叶片6 静压系数下降最多，其大小为0.16。在叶片工作面相对长度为0.5 时，叶片1 的静压系数最大，最大值为0.12。叶片3 的静压系数最小，最小值为0.01。叶片1～6 工作面静压系数方差分别为0.109，0.093，0.074，0.271，0.293，0.255。可见，叶片1 工作面受到蜗舌的影响，压力变化波动相对较大。在整个工作面上，叶片1 压力的变化幅值为1.13，叶片6 压力的变化幅值为0.99。叶片1、2、4 工作面压力系数在相对长度为0.3～0.6范围内高于其他叶片，在相对长度大于为0.6 时压力系数低于其他叶片。

从图10b 中可以看出，叶片1～6 背面静压系数最大值分别为0.58, 0.59, 0.58, 0.57, 0.58, 0.56，最小值分别为-0.32, -0.32, 0.34, -0.30, -0.29, 0.31。在叶片进口处，背面的静压系数最大值均在0.58 左右，叶片4 的背面静压系数值最小。各叶片背面压力系数在相对长度低于0.8 的范围内变化较小且有相同趋势。在相对长度高于0.8 的范围各叶片压力系数均有所上升，其中叶片6 上升幅度最大，最大值为0.06。叶片1～6背面静压系数方差分别为0.048, 0.063, 0.057,0.059, 0.059, 0.043。可见，在整个叶片背面，叶片2 背面压力变化波动最大。在叶片相对长度小于0.4时，叶片背面静压系数值为正值。在相对长度为0.9时，叶片背面各叶片的静压系数值相差较大，其中，叶片2 的静压系数值为-0.27，叶片6 的静压系数值为-0.16，两者差值为0.11。在相对长度小于0.5 时，叶片1、6 的背面静压值要低于其他叶片的，在相对长度大于0.5 时，叶片1、6 背面的静压值大于其他叶片。叶片背面的静压值叶片背面相较工作面的变化相对平稳。

总的来说，随着相对长度的增加，叶片上的静压系数总体呈下降趋势。背面的静压系数要高于工作面的静压系数，叶片工作面的静压系数变化幅度略低于背面。

2）速度场分布

图11 所示为设计工况下泵及泵作透平轴面速度分布图。

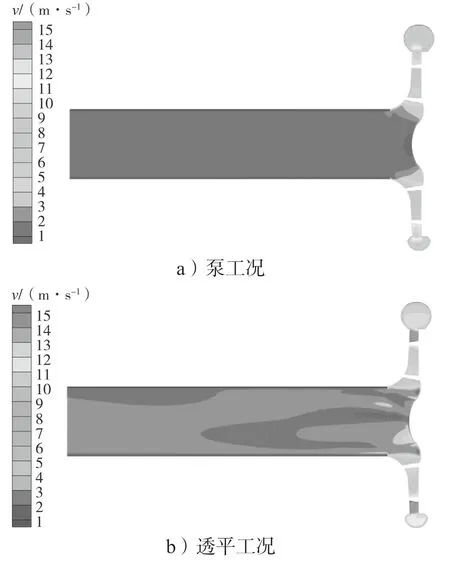
图11 泵及泵作透平最优工况下的轴面速度云图Fig.11 Axial plane velocity cloud map of pump and pump as the turbine under optimal conditions

泵和透平轴平面平均速度分别为2.08, 2.72 m/s。泵进口流道内流速较为均匀，在叶轮区域由于叶轮做功，流体速度逐渐增加且分层明显，蜗壳与叶片交界处流速达最大值，泵流道内流速最大值为12.5 m/s。透平流道内流速最大值为16.7 m/s。泵在入口流道内的流速为1～3 m/s，进入叶轮区域后流速急剧增大，在叶片尾缘达到最大。泵和透平在蜗壳中的速度大致相同，速度大小为10～12 m/s。透平在出口流道内的流速为1～5 m/s，透平流速从蜗壳到出口流道逐渐减少且存在分层现象，在出口流道内存在速度波动。

图12 所示为泵及泵作透平在最优工况下的速度分布。从图中可以看出，泵出口流速为1～5 m/s 且分布不均匀，蜗壳流道内流体流速为6～8 m/s，叶片工作面流速为1～5 m/s，叶片背面流速为3～6 m/s 且叶片工作面相对长度在0.3～0.7 之间流体速度较低，该区域流体流速为1～3 m/s。透平入口段速度分层明显，蜗舌处的速度较大，可达13.5 m/s。受动静干涉影响，蜗壳内的流速不稳定，其速度变化在8～15 m/s 之间，靠近蜗壳壁面的速度相对较小。透平叶片工作面速度为1～4 m/s，背面速度为7～10 m/s，与泵不同的是，透平叶片工作面在相对长度为0.5～1.0 之间的流体流速最低，该区域流速为1～3 m/s。

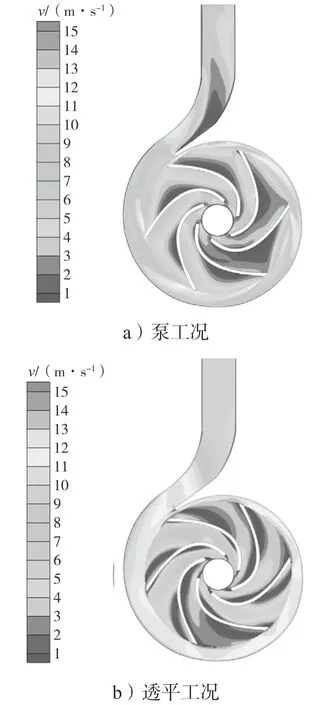
图12 泵及泵作透平最优工况下的速度分布云图Fig.12 Turbine velocity distribution of pump and pump as the turbine under optimal conditions

泵及泵作透平在叶片工作面的速度低于背面速度，因为叶片是有限个数，这与液体在流道内产生的速度滑移有关。透平入口到蜗舌透平的速度逐渐增大且分层明显，其中包含静动压力转化。透平叶片工作面速度分布均匀，蜗壳与叶轮入口处存在动静干涉。设计工况下泵及泵作透平中间平面的速度流线分布图，如图13 所示。

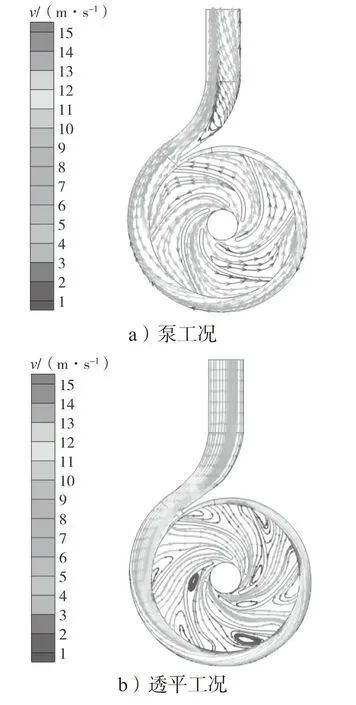
图13 泵及泵作透平最优工况下的速度流线分布云图Fig.13 Turbine velocity streamline distribution of pump and pump as the turbine under optimal conditions

从图13 中可以看出，叶轮各个流道内其速度分布十分规律，其内部从叶轮背面到叶轮的工作面，速度的变化趋势是逐渐减小的。由此可以看出，叶轮流道内部的流体速度增加的原因是受到了旋转的叶轮作用，叶轮将能量源源不断地传递给流体。还可以发现，在流体从叶轮出口流出到达蜗壳内部时，流体速度的变化规律是先变大、后变小，这是因为流体受到了叶轮作用，到达出口时的动能增大，之后扩散进入蜗壳后流体被降速增压，速度能转化为压力能。在透平的工作面进口处附近都有较大的漩涡，该漩涡的旋转方向与叶轮的旋转方向相反。叶片背面出现脱流现象，也存在漩涡，此漩涡旋转方向与叶轮方向一致，强度弱于工作面的漩涡。