Study on anti-faulting design process of Urumqi subway line 2 tunnel crossing reverse fault

An Shao Tao Lianjin,2 Bian Jin

(1Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China)(2Center of Cooperative Innovation for Beijing Metropolitan Transportation, Beijing University of Technology, Beijing 100124, China)(3Maritime Engineering College, Guangdong Ocean University, Zhanjiang 524088, China)

Abstract：For the tunnel crossing active fault, the damage induced by fault movement is always serious. To solve such a problem, a detailed anti-faulting tunnel design process for Urumqi subway line 2 was introduced, and seven three-dimensional elastic-plastic finite element models were established. The anti-faulting design process included three steps. First, the damage of tunnel lining from different locations of fault rupture surfaces was analyzed. Then, the analysis of the effect on tunnel buried depth was given. Finally, the effect of the disaster mitigation method on the flexible joint was verified and the location of the flexible joint was discussed. The results show that when the properties of surrounding rock at the tunnel bottom grows soft, the tunnel deformation curve is smoother and tunnel damage induced by fault movement is less serious. The vertical displacement change ratio of secondary linings along the tunnel axis may be the main factor to cause shear damage to the tunnel. The interface between the hanging wall and fracture zone is defined as the most adverse fault rupture surface. The tunnel damage was reduced with the decrease in the tunnel buried depth as more energy was dissipated by overburden soil and the differential uplift zone of soil became more diffuse. The method of the flexible joint can reduce the tunnel damage significantly and the disaster mitigation effect of different locations on the flexible joint is different. The tunnel damage is reduced by the greatest degree when the flexible joint is located on the fault rupture surface.

Key words：subway tunnel; finite element method; anti-faulting design process; fault rupture surface; buried depth; flexible joint

Urban tunnels are used to accommodate lifelines such as subways, sewer systems, roads and so on, which are closely related to the sustainable development of the city[1-2]. However, many cities have multiple faults, which presents an enormous challenge for building tunnels. The building codes of many countries recommend avoiding construction in the fault zones, but it is not always possible to avoid construction of the tunnel near an active fault[3].

China is one of the most seismically-active regions and bears great risk for the occurrence of fault dislocation. Major cities in China such as Beijing, Urumqi and Taiyuan are located in seismically-active zones with many faults, meaning that it is inevitable for tunnels in some cities to cross one or more fault zones due to urban development of transportation. For example, the tunnel in the newly-established Urumqi subway line 2 crosses four fault zones in total, including the Jiu Jiawan fault, Bagang-Shihua fault, Xi Shan fault and Yamarik fault. The underground structures crossing active faults are subjected to both fault dislocation and seismic shaking when earthquakes occur. Many scholars believe that the fault dislocation is the main factor of underground structure damage[4-5]. Comprehensive studies have been conducted to fully explain this phenomenon[6-10]. These studies indicate that it is necessary to design for minimizing the damage caused by fault dislocation. The previous research on this subject included the methods of field study[11-13], model experiment[14-19]and numerical simulation[20-24]. The research on an active tunnel crossing fault can be divided into three stages in terms of time: Damage analysis of tunnel lining, the analysis of correlated influence factors and the study on the disaster mitigation method. The above research process provides a basic design framework for engineering applications, but some specific and key issues listed below remain to be addressed.

For example, the previous studies always assume that the fault rupture surface occurs at a fixed position (inside the fracture zone or at its boundary). In fact, the location of the fault rupture surface is difficult to predict and it is not reasonable to only assume that the fault rupture surface occurs at a fixed position for faults running cross a large width of the fracture zone. Besides, the effects of fault dip angle, fault displacement, fault type, tunnel thickness and tunnel diameter on tunnel damage have been studied by many scholars, but for an underground tunnel project, the above influence factors have been determined and attention should be paid on the influence factor that may change due to construction requirements. Finally, the articulated design with the flexible joint is proved to be effective. When the distance between the flexible joint and fault rupture surface differs, the tunnel damage may also vary. Thus, it is necessary to study the location of the flexible joint.

Summarized by previous research progress and existing problems, the detailed design process of the project of Urumqi subway line 2 tunnel crossing active fault zone is given. The design process includes three steps, the damage analysis of tunnel lining considering different locations of the fault rupture surface, the analysis of influence factors, and the effect of the disaster mitigation method on the flexible joint and its location. It is expected that the above research results can be referenced when the underground structures crossing active fault are designed.

1 Urumqi Subway Line 2 Tunnel

Urumqi subway line 2 tunnel is one of the subway tunnels under construction in the region of northwest China which is supposed to be completed in next few years. This metro tunnel is 19.1 km long with the diameter of 6.7 m, which closely connects the recent key development areas of the city. The site is located in the Tian Shan region which contains multiple faults. The focus of this paper is the Xi Shan fault and the width of the fracture zone is 52 m. A longitudinal profile of geological formations along the tunnel axis is shown in Fig.1. It can be seen that the depth of overlying soil is 12 m; the vertical distance from the tunnel bottom to the fracture zone is 0.7 m and the dip angle of the fault is 45°. To keep the tunnel work for a life period of 100 years, the fortification vertical fault displacement calculated by the probability method[25]is determined to be 16.5 cm.

2 Anti-Faulting Design Process

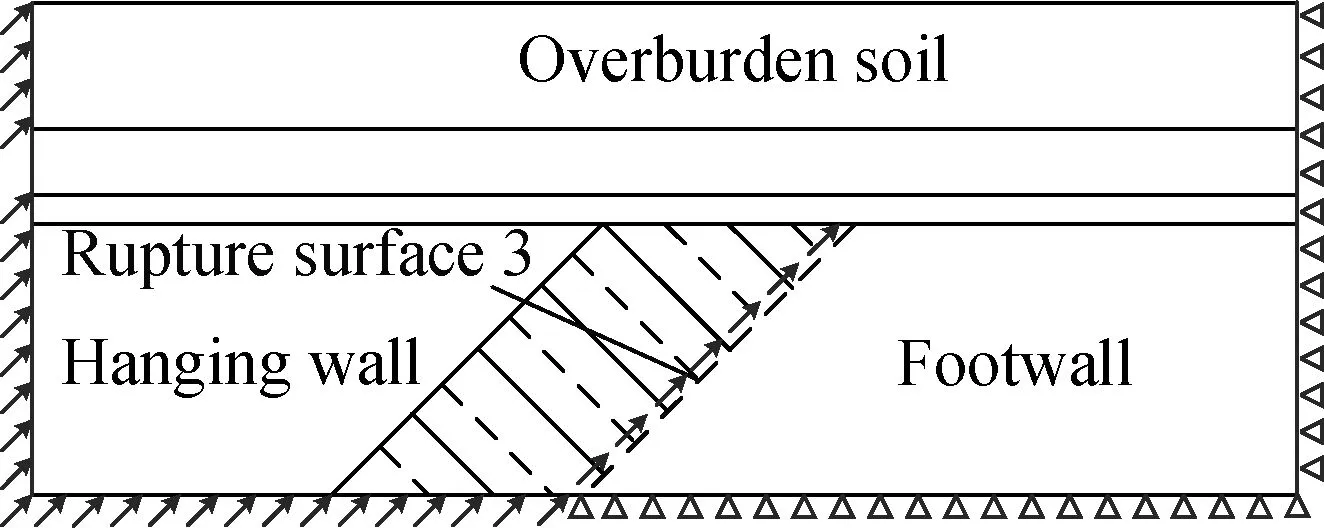
Combining the characteristics of the project, the anti-faulting design process is listed in Fig.2. As the width of the fracture zone is large and the properties of surrounding rocks vary greatly along the longitudinal direction, different locations of the fault rupture surface are considered in this paper. The fault rupture surface is assumed to be located at the contact surface between the hanging wall and fracture zone, the center of the fractured zone, and the surface between the footwall and fracture zone, respectively. The purpose of this step is to discuss the most adverse rupture surface by analyzing and comparing the damage of tunnel lining. Then, the influence law of buried depth on the tunnel damage is emphatically analyzed, since buried depth may change due to construction requirements. Finally, the disaster mitigation effect of the flexible joint is verified and the suitable location of the flexible joint for the engineering is discussed.

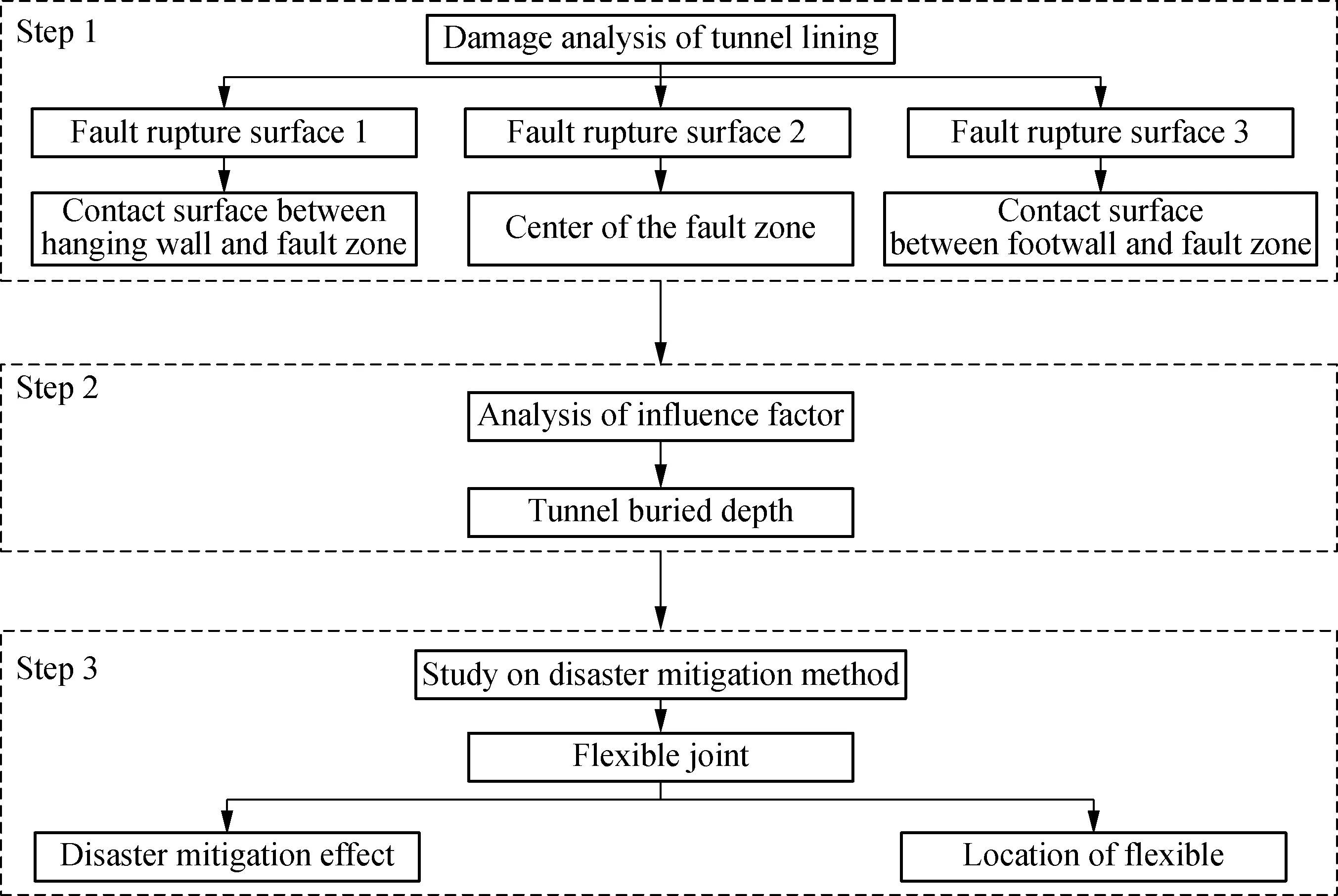
Fig.2 Anti-faulting design process

3 Numerical Model

3.1 Soil-tunnel model

The pattern of longitudinal deformations is determined by means of the finite element commercial software, ABAQUS 2017. The longitudinal length of the model is determined to be 252 m by trail calculations until the response of tunnel lining ceases to change. The size of the soil-tunnel model is 252 m × 68 m × 60 m (length × width × height), and the soil and tunnel are simulated by the element C3D8R(see Fig.3). According to the Chinese Code for Design of Road Tunnel[26], the mudstone and coal seam are regarded as Ⅴ-grade surrounding rocks, and the silty clays and boulder are regarded as Ⅵ-grade surrounding rocks. The physico-mechanical properties of soil layers are presented in Tab.1. All the soil layers are simulated by the solid elements and the Mohr-Coulomb yield criterion is used for the their constitutive models. The mine tunneling method is adopted during the construction process, and C45-grade concrete, which is consistent with the Chinese Code for Design of Concrete Structures[27], is used for initial support simulated by the solid element with a thickness of 35 cm and C50-grade concrete is used for the secondary lining simulated by the solid element with its thickness of 25 cm. The initial support and secondary lining are bound together in this simulation.

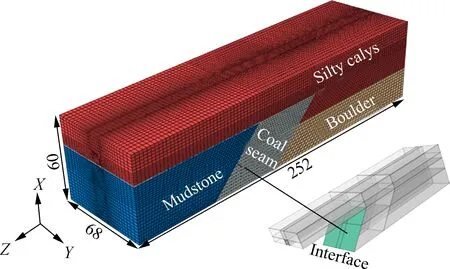
Fig.3 3D finite element model of soil-tunnel system (unit:m)

Tab.1 Physico-mechanical properties of soil layers

3.2 Constitutive model of concrete

The elastic constitutive model is often used for lining structures[28-30]. However, the internal structure of concrete is complex in both the macro and micro sizes. It is not comprehensive and reasonable to use the linear elastic constitutive model to describe the properties of concrete. The damage plasticity constitutive model for concrete (CDP model), considering concrete strain softening, stiffness degradation and inelastic strain evolution, was proposed by Lubliner et al.[31]and improved by Lee et al[32]. Damage parameters are involved to reflect the damage mechanism of the concrete under loading. The CDP model was adopted in this model to simulate the mechanical response of concrete. The CDP model includes two parts: 1) The stress-strain curve of concrete under compressive and tensile loading, respectively; 2) The damage parametersdtanddcunder tension and compression. The stress-strain curve for concrete is adopted according to the Chinese code for design of concrete structures and it is expressed as follows:

For tension,

σ=(1-ct)Ecε

(1)

(2)

(3)

(4)

whereEcis Young’s modulus;ctis the evolution parameter of tensile damage;εis the strain;εt,ris the peak tensile strain corresponding to the peak tensile stress;ft,ris the peak tensile stress. For C45-grade concrete,εt,r=1.072 2×10-4,ft,r=2.51 MPa; for C50-grade concrete,εt,r=1.100 8×10-4,ft,r=2.64 MPa.αtis the parameter of the falling part of stress-strain curve. For C45-grade concrete,αt=1.967 2; for C50-grade concrete,αt=2.190 8.

For compression,

σ=(1-cc)Ecε

(5)

(6)

(7)

(8)

(9)

whereccis the evolution parameter of compressive damage;fc,ris the peak compressive stress;εc,ris the peak compressive strain corresponding to the peak tensile stress. For C45-grade concrete,εc,r=1.633 6×10-3,fc,r=29.6 MPa; for C50-grade concrete,εc,r=1.678 4×10-3,fc,r=32.4 MPa.αcis the parameter of the falling part of stress-strain curve. For C45-grade concrete,αc=1.336; and for C50-grade concrete,αc=1.504.

The damage parameters are derived using the energy equivalence principle proposed by Sidoroff[33]:

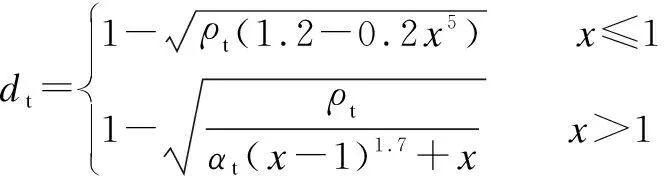
(10)

(11)

The physical parameters of concrete linings are listed in Tab.2.

Tab.2 Material properties of concrete

3.3 Contact and boundary

The Coulomb friction law is used to simulate the tangential mechanics behaviors between the soil and tunnel and it can be expressed as

τcrit=μP

(12)

whereτcritis the critical value of the shear stress. When the tangential contact shear stress is larger than the critical shear stressτcrit, slipping will occur on the interface.μis the friction coefficient of the contact interface (0.4 in this paper) andPis the contact compressive stress. In the model, surface to surface contact interaction is considered between the fault area and both sides of surrounding rock. The friction coefficient between them is set to be 0.21(μ=tan(2φ/3))[34].φis the friction angle of the fault zone.

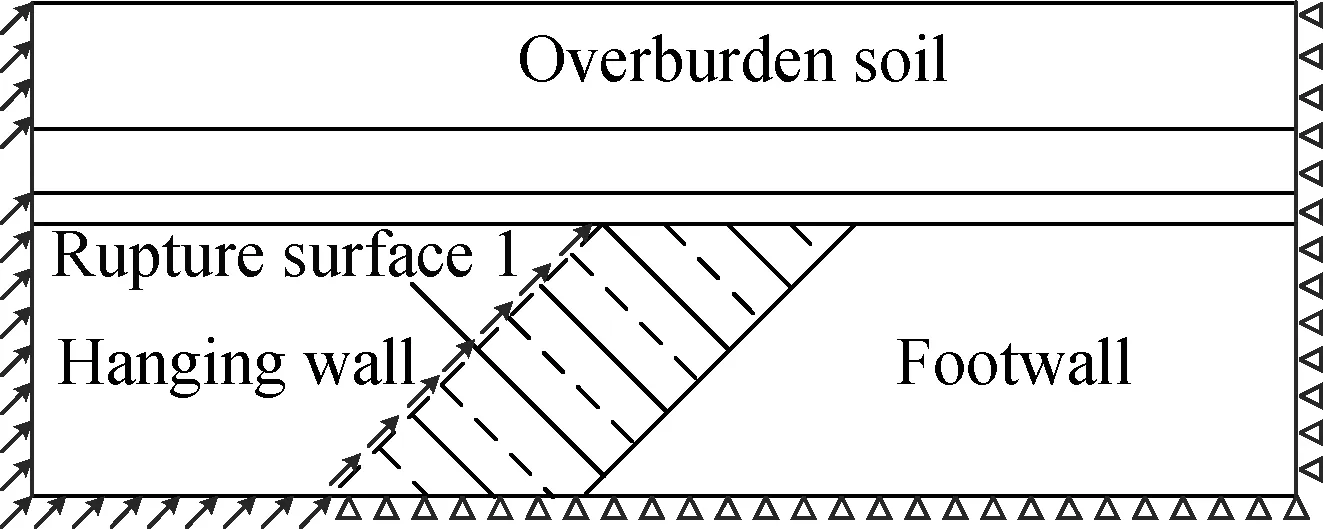
The simulation includes three steps: the balance of in-situ stress, tunnel excavation and the application of the displacement load by the quasi-static method. As for boundaries, the normal directions on all sides and bottom boundaries are constrained in the first two steps. In the last step, the side and bottom boundaries of the hanging wall is free and the fault displacement is applied to the corresponding position, as shown in Fig.4.

4 Results and Discussion

4.1 Damage analysis of secondary linings of different fault rupture surfaces

In this section,the damage analysis of the shallow subway tunnel under the action of fault dislocation is investigated. The deformation, plastic strain, shear strain, tensile-crack damage and the compressive damage of secondary linings considering different locations of the fault rupture surface are analyzed and compared.

4.1.1 Deformation of secondary lining

Fig.5 shows the crown vertical displacement distribution curves of secondary linings of different fault rupture surfaces in the longitudinal direction. The boundary of the hanging wall in the soil-tunnel model is set as the zero point, and the direction from the hanging wall to footwall is defined as the positive direction. The fault dislocation occurs at longitudinal coordinates of 100, 126 and 152 m, respectively. It can be seen that the secondary linings become an “S” shape after undergoing fault displacement.

(a)

(b)

(c)

Fig.4Boundary conditions in the analysis of last step. (a) Rupture surface 1;(b) Rupture surface 2; (c) Rupture surface 3

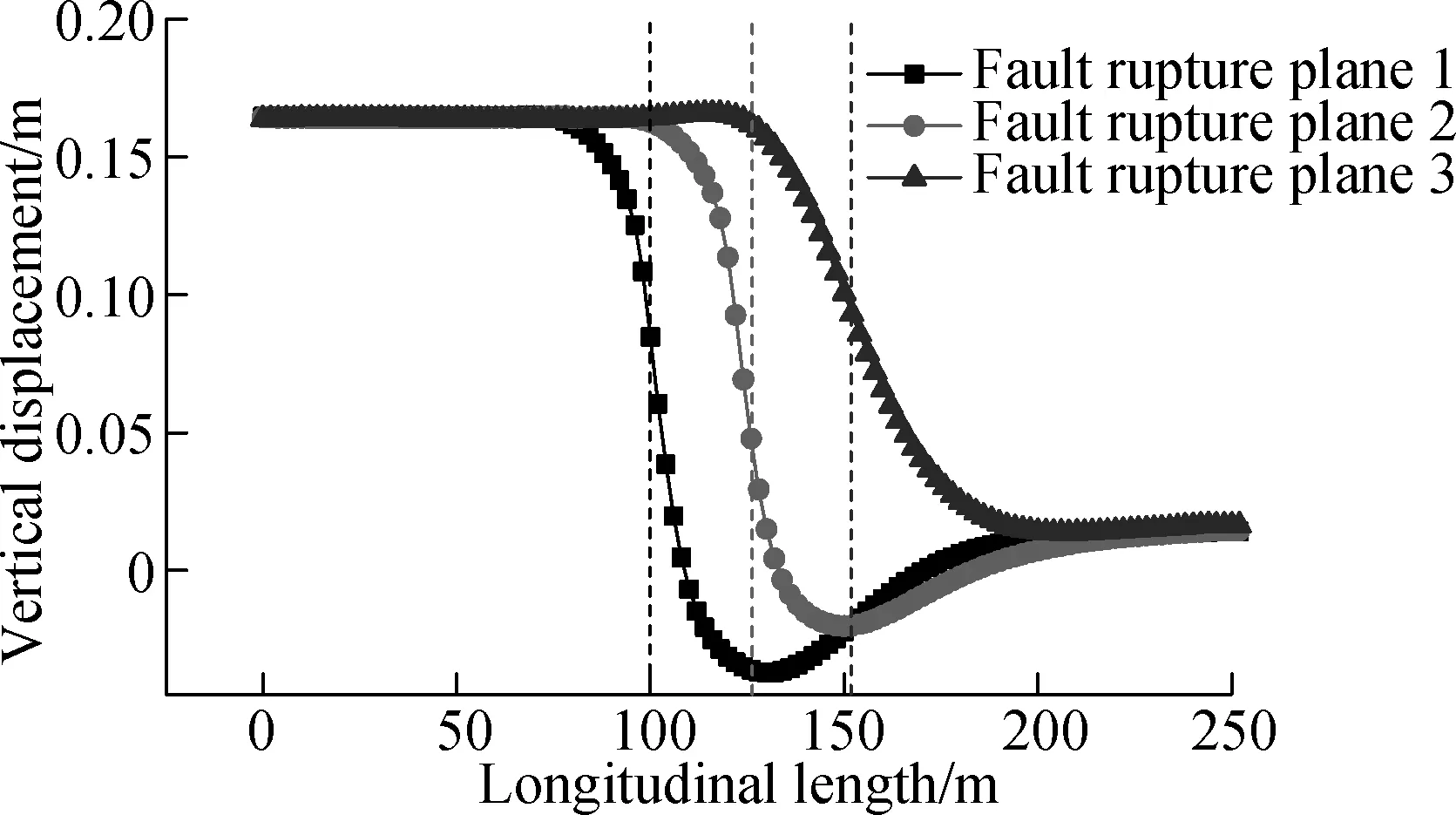
Fig.5 Vertical displacement distribution curves of secondary linings in the longitudinal direction

The vertical displacement change ratio is equal to the slope of the curve in Fig.5. The maximum slope from fault rupture surface 1 to surface 3 is 0.012 18, 0.011 66 and 0.003 74 (absolute value), respectively; and the corresponding longitudinal coordinate is 102, 128 and 152 m. The slope of fault rupture surface 1 is the largest and that of fault rupture surface 3 is the smallest, indicating that the deformation of the secondary lining from fault rupture surface 1 to surface 3 is increasingly becoming smooth. The reason for the above phenomenon is that the properties of the surrounding rocks at the tunnel bottom are different. When the soil is softer, the deformation becomes smaller.

4.1.2 Plastic strain

The maximum plastic strain of secondary linings of different fault rupture surfaces are shown in Fig.6. It can be seen that the maximum plastic strain from fault rupture surface 1 to surface 3 are 1.444×10-2,1.369×10-2and 2.708×10-4, respectively, which decreases gradually. Compared with the maximum plastic strain of fault rupture surface 1, the plastic strain of fault rupture surface 2 decreases by 5.19% and that of fault rupture surface 3 decreases by 98.12%. The maximum plastic strains of fault rupture surfaces 1 and 2 occur at the spring line. The plastic zone is distributed in both the stationary and moving sides, while the maximum plastic strain of the fault rupture surface 3 appears at the invert, and the plastic zone is distributed in the moving side. Combined with the comparative analysis of plastic strain of different fault rupture surfaces, it can be concluded that the soft soil can reduce tunnel damage induced by fault dislocation.

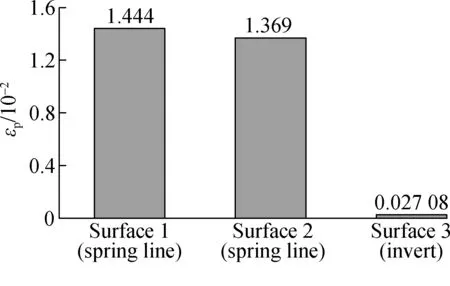
Fig.6 Maximum plastic strain of secondary linings

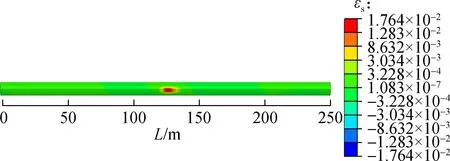
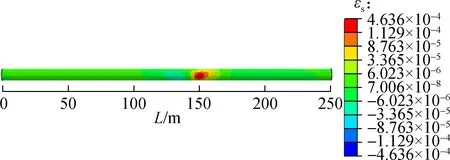
4.1.3 Shear strain

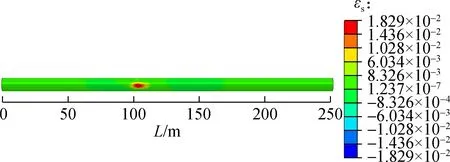
The shear strain of secondary lining is distributed symmetrically along tunnel axis under the action of fault displacement. The shear strain distribution contours of secondary linings are shown in Fig.7 (front view), it can be seen that the maximum shear strain of different fault rupture surfaces occurs at the spring line. The maximum shear strain from fault rupture surface 1 to surface 3 is 1.829×10-2, 1.764×10-2and 4.636×10-4, respectively, which decreases gradually. Compared with the maximum shear strain of fault rupture surface 1, the shear strain of fault rupture surface 2 decreases by 3.55% and that of fault rupture surface 3 decreases by 98.52%. The ratio of shear strength to compressive strength of concrete is about 0.095 to 0.121[35]. The shear modulus of concrete is 40% of its Young’s modulus[36]. Thus, the critical value of shear strain is expressed as

(13)

According to Eq.(13), the shear strain critical value of secondary lining is 2.841×10-4, which is less than the shear strain of tunnel linings in Fig.7, indicating that the tunnel lining suffers shear damage. The longitudinal coordinate of the maximum shear strain from fault rupture surface 1 to surface 3 is 102, 128 and 152 m, respectively, which is consistent with those of the maximum vertical displacement change ratio. In addition, both the vertical displacement change ratio and the shear strain increase at the beginning and then decrease, and the above analysis indicates that the longitudinal vertical displacement change ratio may be the main factor causing shear damage to the tunnel.

(a)

(b)

(c)

Fig.7Shear strain distribution contour of the secondary lining. (a) Fault rupture surface 1; (b) Fault rupture surface 2; (c) Fault rupture surface 3

4.1.4 Tensile-crack damage of secondary lining

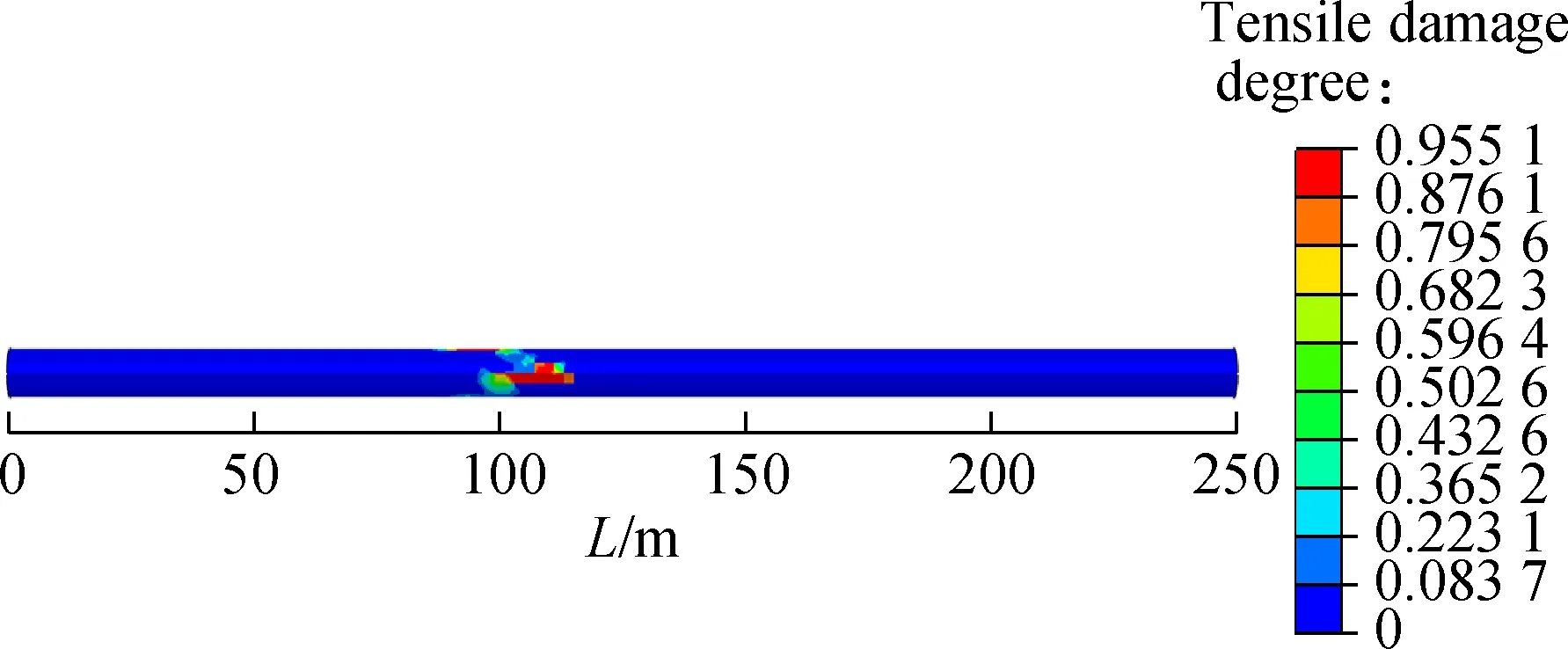
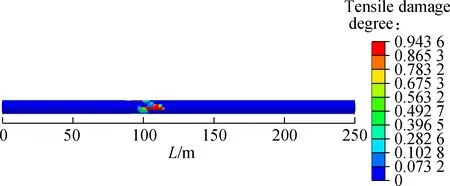
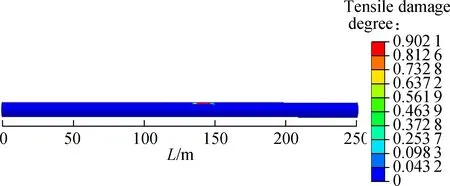
In the CDP model, the tensile (or compressive) damage is defined to measure structural tensile (compressive) damage with a variable range from 0 to 1. The value of 0 indicates that there is no tensile (compressive) damage in structural components, and the value of 1 indicates that structural components are completely damaged.Fig.8 shows the tensile damage parameter (DAMAGET) distribution contours of secondary linings of different fault rupture surfaces. The tensile damage is mainly concentrated at the crown and spring line. The maximum tensile damage parameter from fault rupture surface 1 to surface 3 is 0.955 1, 0.943 6 and 0.902 1, respectively, and decreases gradually. The tensile damage of fault rupture surfaces 1 and 2 is concentrated at the crown of the moving side and spring line of the stationary side, while the tensile damage of fault rupture surface 3 is only concentrated at the crown of the moving side. Compared with the maximum tensile damage parameter of fault rupture surface 1, the tensile damage parameter of fault rupture surface 2 decreases by 1.2% and that of fault rupture surface 3 decreases by 5.55%.

(a)

(b)

(c)

Fig.8Tensile damage parameter distribution contours of secondary linings.(a) Fault rupture surface 1; (b) Fault rupture surface 2; (c) Fault rupture surface 3

The method proposed by Chen et al.[37]is used to calculate the crack width of the secondary lining in this paper, and the tensile stress-strain curve of concrete is illustrated in Fig.9.

The relationship between the tensile damagedtand the crack widthwtis[38-39]

(14)

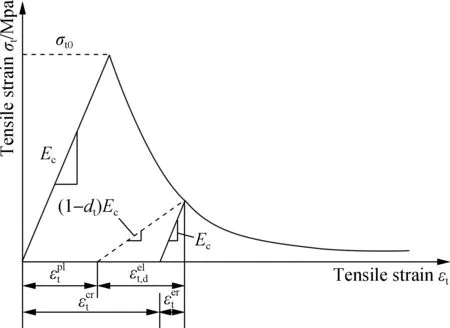
Fig.9 Tensile stress-strain curve of concrete

According to the design code for hydraulic concrete structures[40], the crack widthwt=0.2 mm is defined as the maximum crack width limit and the corresponding tensile parameter for the secondary lining is 0.838 according to Eq.(14). Based on the above analysis, the damage for the secondary lining can be classified and listed in Tab.3.

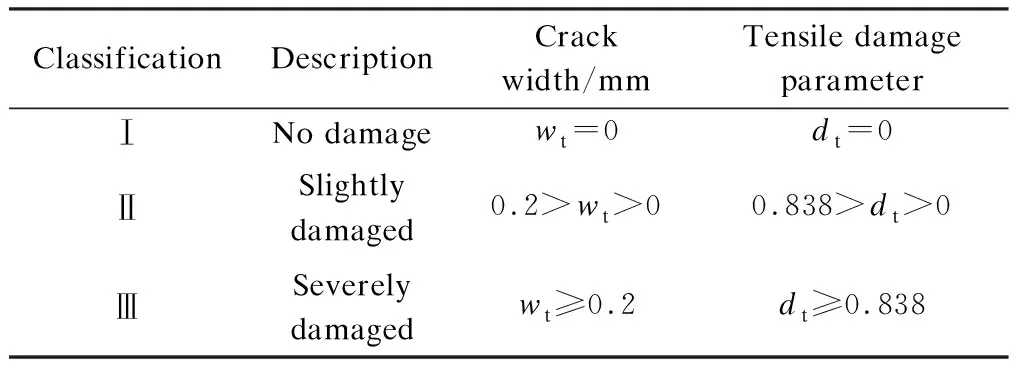
Tab.3 Classification of damage for secondary lining

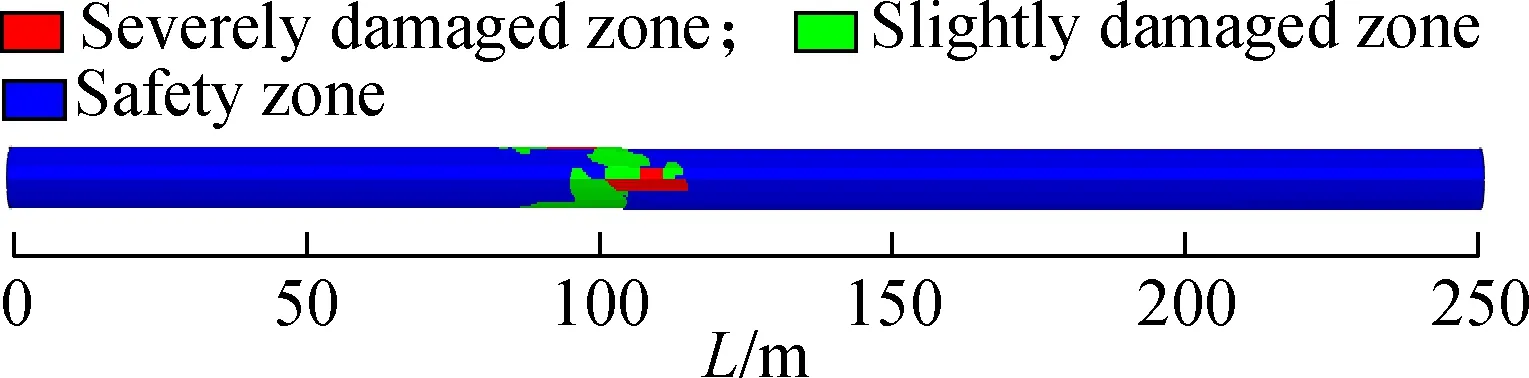
The tensile-crack damage contours of the secondary linings of different fault rupture surfaces are shown in Fig.10 according to the above classification of damage for the secondary lining.

(a)

(b)

(c)

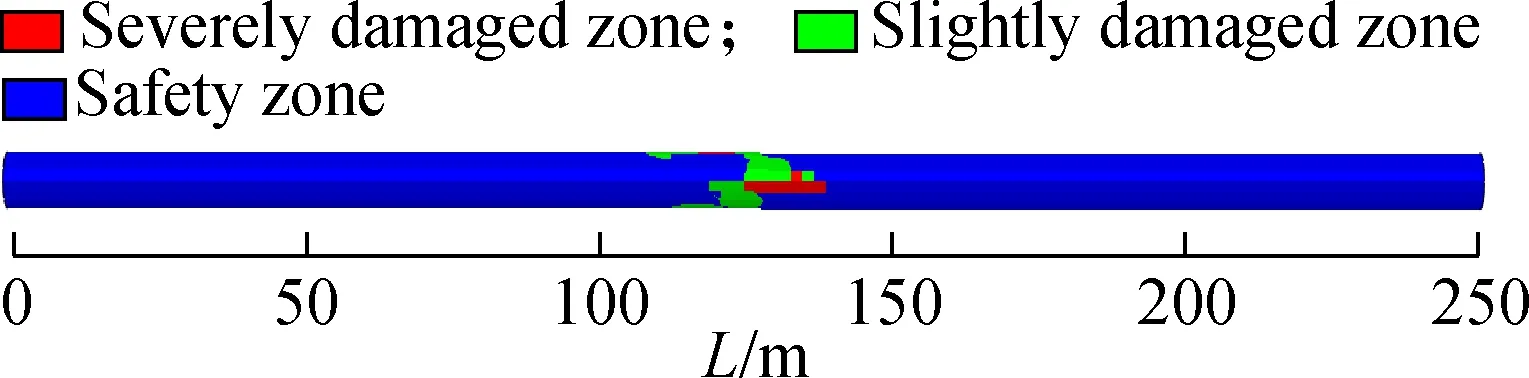
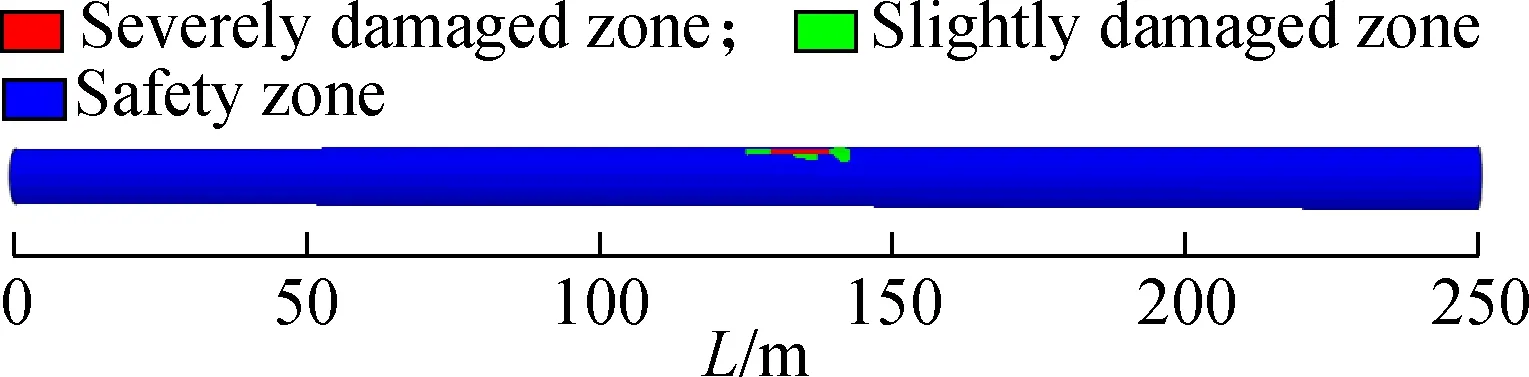
Fig.10Tensile-crack damage contours of secondary linings. (a) Fault rupture surface 1; (b) Fault rupture surface 2; (c) Fault rupture surface 3

As shown in Fig.10, under the action of fortification fault displacement, the crown and spring line of fault rupture surfaces 1 and 2 are severely damaged, while the crown of fault rupture surface 3 is severely damaged.

4.1.5 Compressive damage

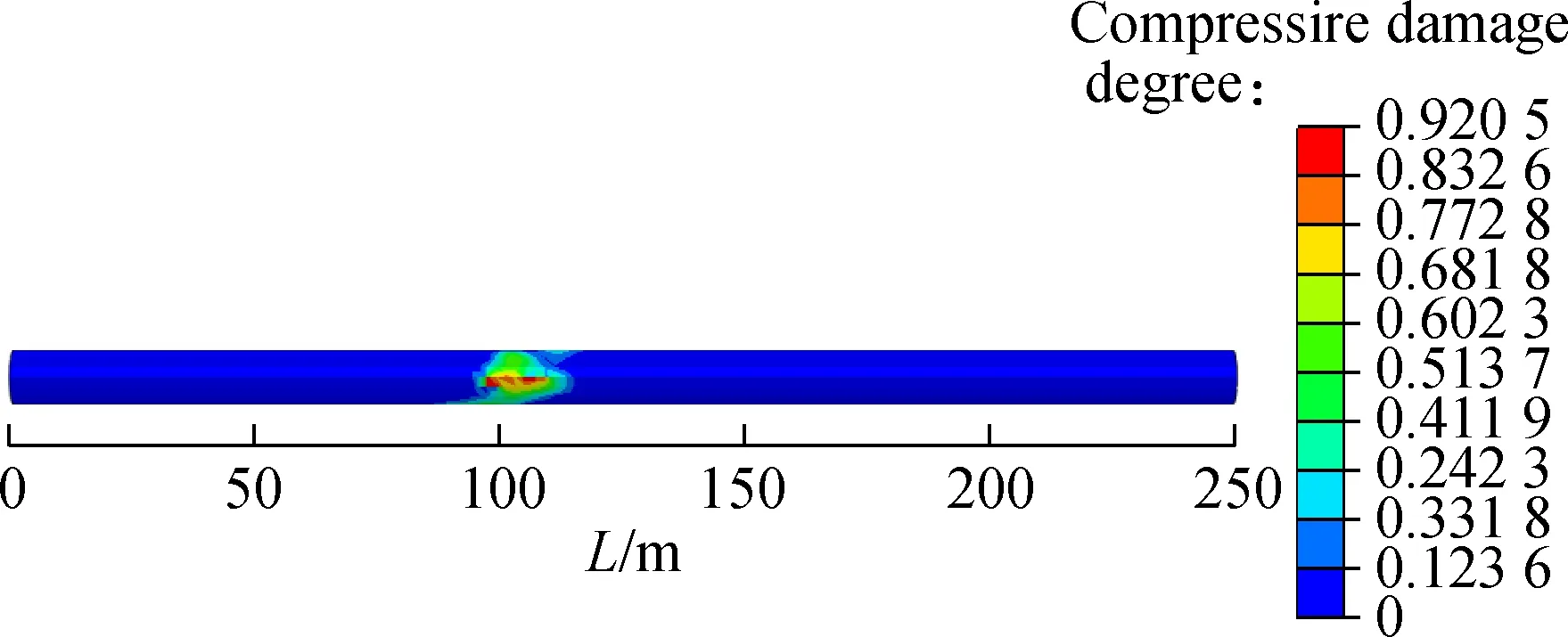
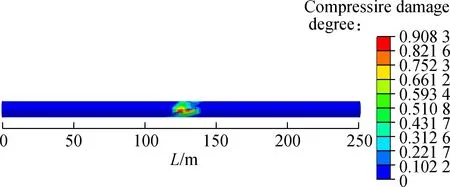
Fig.11 shows the compressive damage parameter (DAMAGEC) distribution contours of secondary linings of different fault rupture surfaces. The compressive damage of fault rupture surfaces 1 and 2 is distributed at the crown, spring line and invert of tunnel, while that of fault rupture surface 3 appears only at the invert. It can be seen that the maximum compressive damage parameter from fault rupture surface 1 to surface 3 is 0.920 5, 0.908 3 and 0.159 4, respectively, which decreases gradually. Compared with the maximum compressive damage parameter of fault rupture surface 1, the maximum compressive damage parameter of fault rupture surface 2 decreases by 1.33% and that of fault rupture surface 3 decreases by 82.68%.

4.1.6 Comparative analysis and interpretation

The maximum plastic strain, shear strain, tensile damage parameter and compressive damage parameter of secondary linings of different fault rupture surfaces and the corresponding change rate (compared to those of fault rupture surface 1) are summarized and listed in Tab.4.

As shown in Tab.4, the maximum value of each index of fault rupture surface 1 is larger than all those of fault rupture surfaces 2 and 3. Thus, fault rupture surface 1 is defined as the most adverse surface. In addition, the maximum value of each index of fault rupture surface 2 is lower than that of surface 1, but the difference is trivial. The reason for this phenomenon is that the surrounding rocks of fault rupture surfaces 1 and 2 are defined as the same grade (Ⅴ-grade) and are similar in properties. The maximum value of each index of fault rupture surface 3 reduces significantly, because the surround-ing rocks of the stationary side of fault rupture surface 3 are rather soft (Ⅵ-grade), and the interaction between soil and tunnel is smaller and apt to the smooth deformation of tunnel linings. With the decrease in damage, the locations of the maximum value of each index vary.

(a)

(b)

(c)

Fig.11Compressive damage factor distribution contours of secondary lining. (a) Fault rupture surface 1; (b) Fault rupture surface 2; (c) Fault rupture surface 3

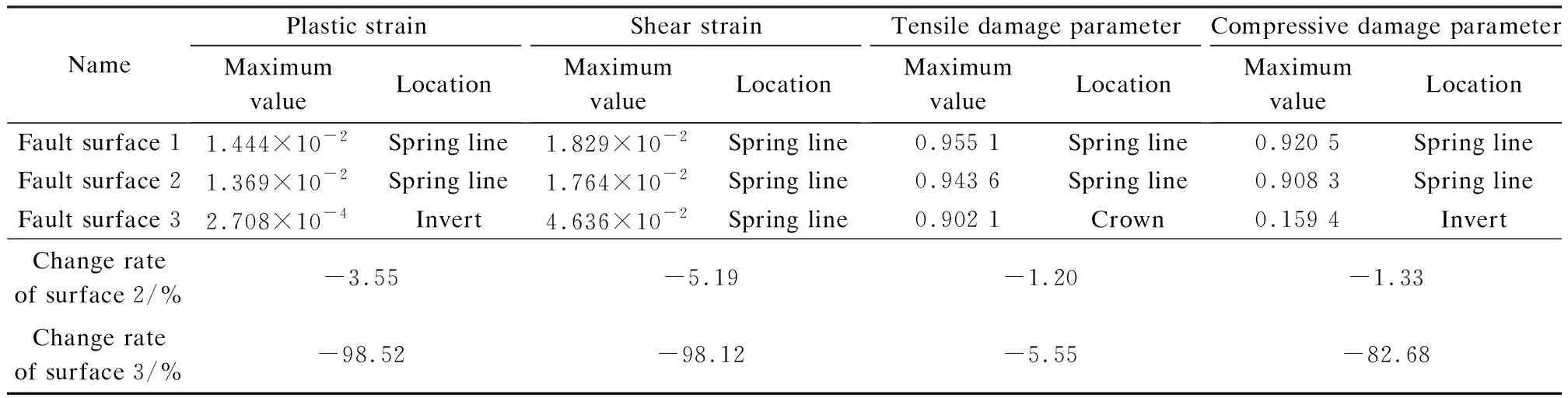
Tab.4 Summary and comparison of each index of different fault rupture surfaces

4.2 Effects of tunnel buried depth on tunnel damage

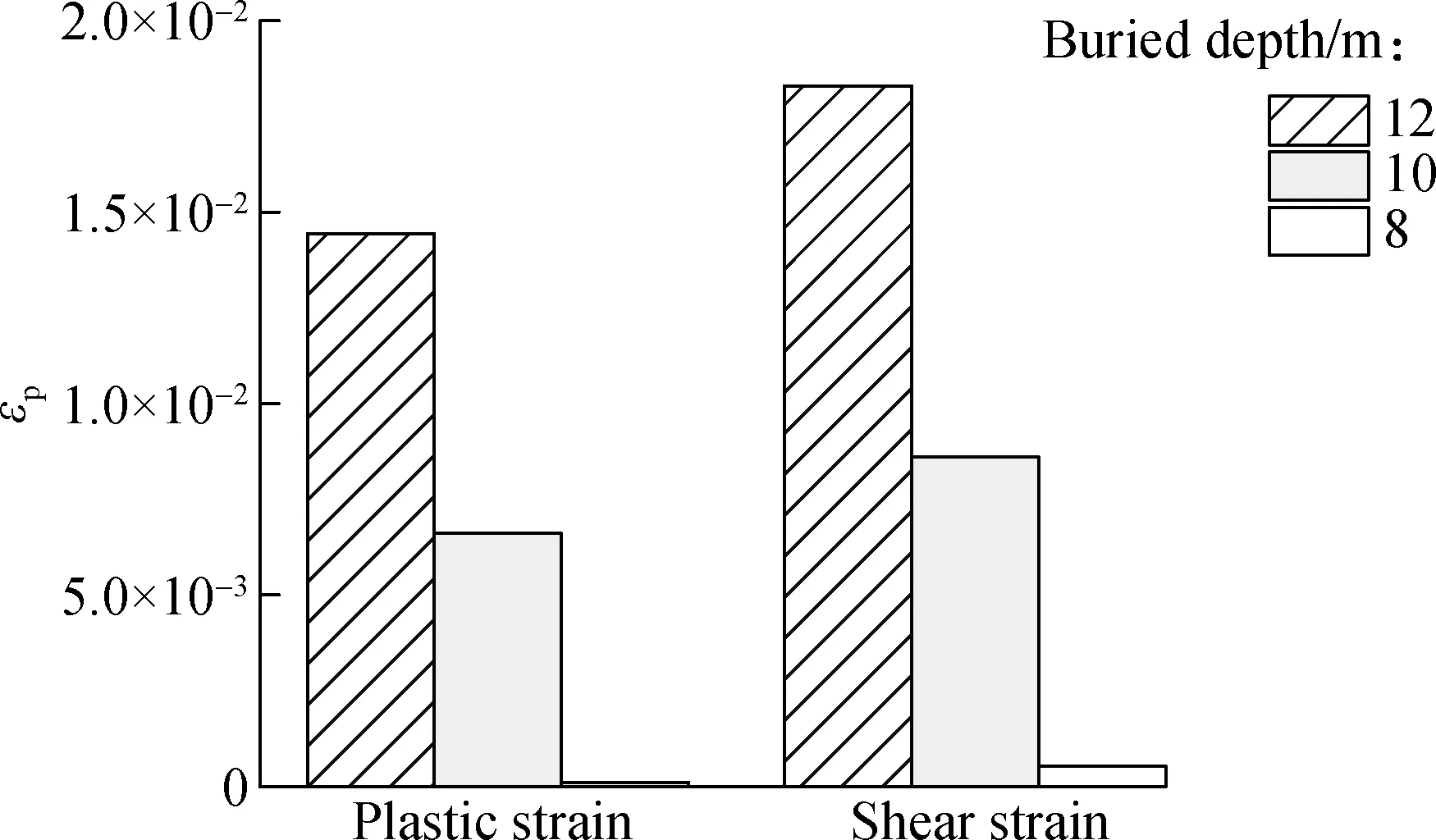
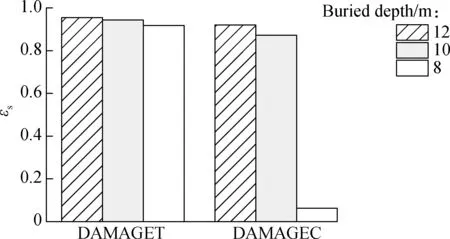
Considering different selections of tunnel buried depth during construction, it is necessary to make an analysis of the effect of buried depth on tunnel damage. When the tunnel buried depth changes from 8 to 12 m, three 3-D soil-tunnel finite element models are established. The fault rupture surface is assumed to be located at the interface between the hanging wall and fracture zone, and the maximum values of plastic strain, shear strain, tensile and compressive damage parameter are obtained and compared in Fig.12. It can be seen that all the indices decrease with the decrease in tunnel buried depth, which indicates that the damage of tunnel has become increasingly slight. The reason is that the vertical distance from the tunnel bottom to fracture zone increases with the decrease in depth. More energy is dissipated by the soil and the differential settlement zone of the soil becomes more diffuse.

(a)

(b)

Fig.12Comparison of each index of different tunnel buried depths.(a) Maximum stress values; (b) Maximum damage parameter values

4.3 Disaster mitigation method

For the tunnel damage induced by fault dislocation in earthquakes, the previous studies proved that the flexible joints are effective[41]. Thus, the method of the flexible joint is adopted for Urumqi subway line 2 tunnel to absorb potential deformation. The interval between the longitudinal coordinates of the maximum positive and negative moment is 32 m. Thus, the consequent flexible joints should not exceed 32 m. Considering that the length of the concrete trolley in tunnel construction is generally 6 to 12 m at present and the spacing cannot be set too small due to the waterproof requirements, the segment length is finally set to be 12 m. The elastic model is used for the flexible joint. The material properties, referencing the flexible joints of Urumqi subway line 1 tunnel, are listed in Tab.5[42].

Tab.5 Physico-mechanical properties of flexible joint

To verify the disaster mitigation effect of the flexible joint and study the mitigation effect from different locations on the flexible joint, two numerical simulation models are established and described as follows:

Case1The middle part of the segment lining is located on the fault rupture surface; namely the flexible joint is 6 m away from the fault rupture surface.

Case2The flexible joint of the segment lining is located on the fault rupture surface.

Both numerical models assume that the fault rupture surface is located at the interface between the hanging wall and fracture zone, and the sketch of tunnel linings with flexible joints is shown in Fig.13.

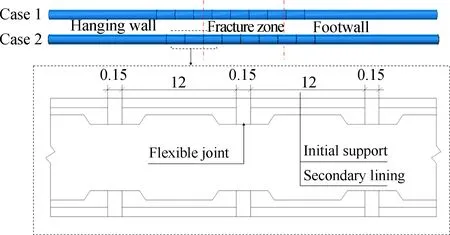
Fig.13 Sketch of tunnel linings with flexible joints (unit:m)

4.3.1 Disaster mitigation effect of the flexible joint ble joints (Figs.6, 7, 8 and 11), it can be seen that the maximum plastic strain decreases by 99.02%; and the maximum shear strain decreases by 98.44%; the maximum tensile damage parameter decreases by 83.15%; the maximum compressive damage parameter decreases by 90.9%, which indicates that the tunnel lining with flexible joints suffers little damage under the action of fortification displacement. In addition, the damage of the secondary lining appears at the locations of the flexible joints. According to the above analysis, the structure close to flexible joints should be strengthened when the method of flexible joint is taken.

Fig.14 shows the contours of each index (plastic strain, shear strain, tensile damage parameter and compressive parameter) of Case 1 after applying fault displacement at the location of fault rupture surface 1. From Fig.14 and compared with damage indices without flexi-

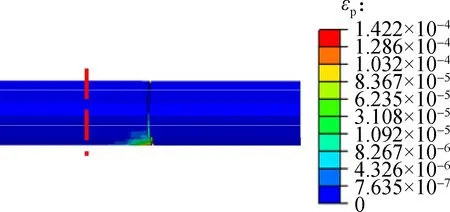
(a)

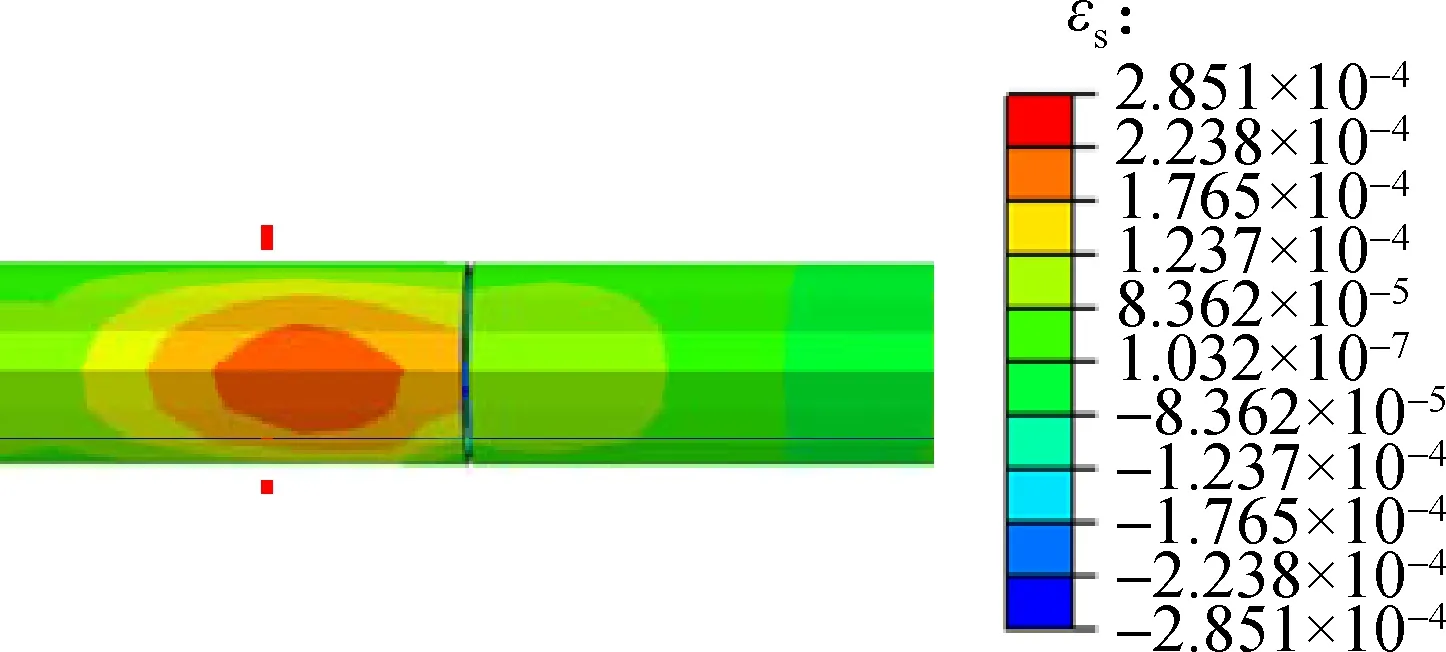
(b)

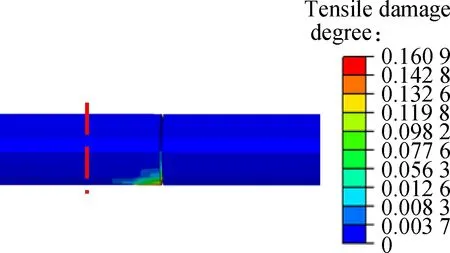
(c)

(d)

4.3.2 Comparison of disaster mitigation effect of the flexible joint in different locations strain decreases by 23.61%; the maximum tensile damage parameter decreases by 81.59%; and the maximum compressive damage parameter decreases by 68.95%, which indicates that the tunnel lining with the flexible joint located on the fault rupture surface shows a better anti-faulting performance. The reason is that the location of the fault rupture surface is where the maximum differential deformation occurs. When the flexible joint is close to the fault rupture surface, it can absorb the deformation of the tunnel lining to the greatest extent. Combining the above analysis, the location of the most adverse surface is where the flexible joint must be set. Thus, the flexible joint should be set at the location between the hanging wall and fracture zone, and the positions of other flexible joints can be deduced and obtained.

Fig.15 shows the contours of each index of Case 2 after applying fault displacement at the location of fault rupture surface 1. Compared with the maximum value of each index in Fig.14, it can be seen that the maximum plastic strain decreases by 68.94%; the maximum shear

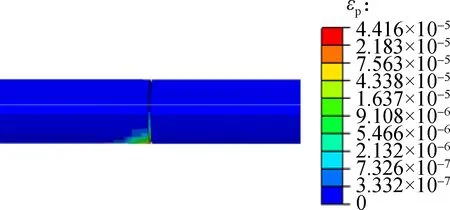
(a)

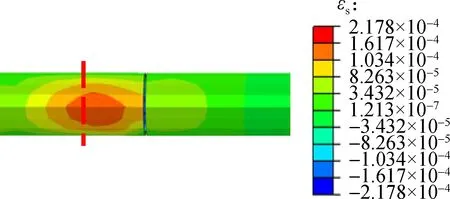
(b)

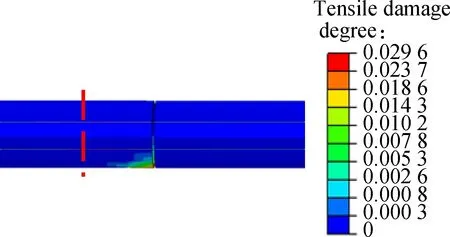
(c)

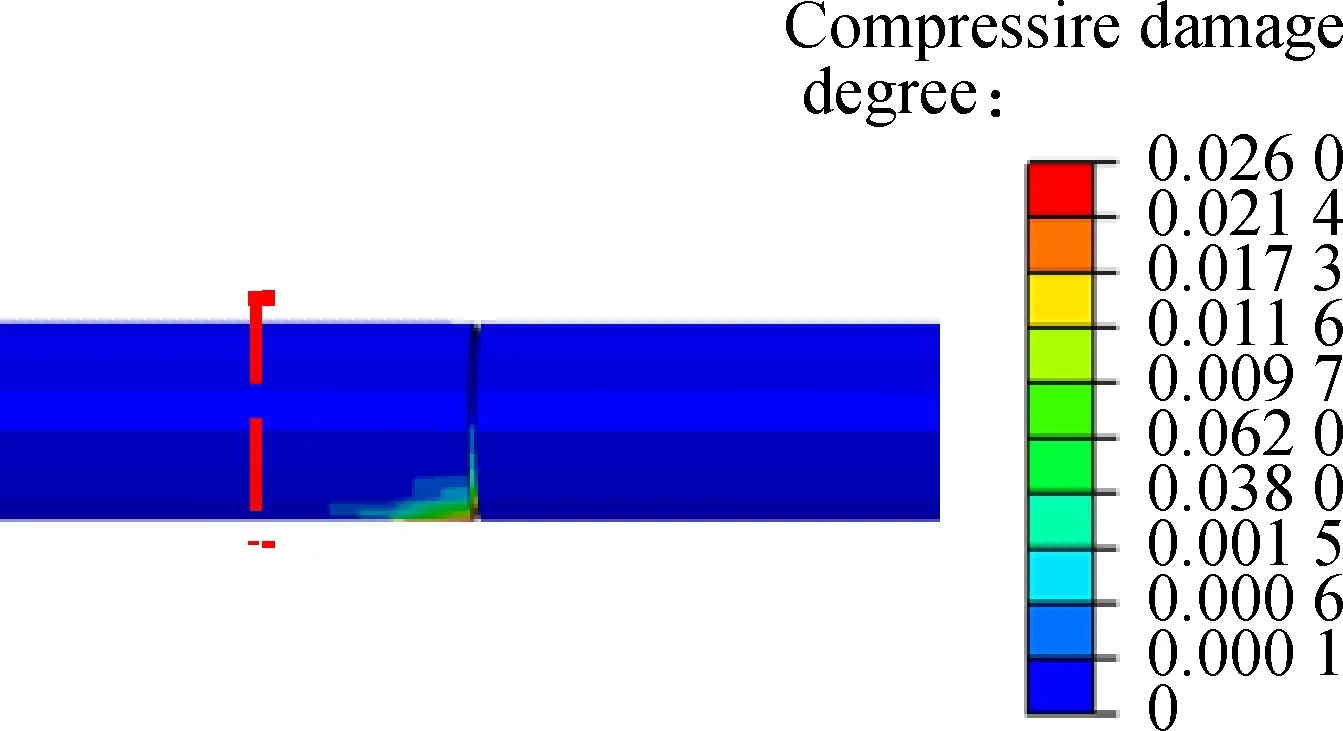
(d)

5 Conclusions

1) Under the action of fault dislocation, if surrounding rock is softer, the deformation of the tunnel is smoother and the maximum slope is smaller. The interface between the hanging wall and fracture zone (fault rupture surface 1) is defined as the most adverse surface and it can be used as the standard surface for enveloping method design.

2) The maximum slope of secondary linings towards the longitudinal direction appears at the same longitudinal coordinates, and so does the maximum shear strain of the spring line of the three fault rupture surfaces. Therefore, the longitudinal vertical displacement change rate may be the main factor to cause shear damage to the tunnel.

3) With the decrease in the tunnel buried depth, the damage of the tunnel induced by fault movement drops, so the tunnel buried depth should be reduced as much as possible after the design requirements are satisfied.

4) The method of the flexible joint can reduce the damage significantly. The damage of the tunnel lining with the flexible joint is concentrated near the flexible joint near the fault rupture surface, so the structure close to the flexible joint should be strengthened. In addition, the tunnel damage caused by fault movement is reduced by the greatest degree when the flexible joint is located on the fault rupture surface.