UAV trajectory planning algorithmfor data collection in wireless sensor networks

Yan Feng Chen Jiahui Wu Tao Li Hao Pang JingmingLiu Wanzhu Xia Weiwei Shen Lianfeng

(1National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)(2Jiangsu Zhongli Electronic Information Sci-Tech Co., Ltd., Changshu 215542, China)(3Science and Technology on Near-Surface Detection Laboratory, Wuxi 214035, China)

Abstract：In order to maximize the value of information (VoI) of collected data in unmanned aerial vehicle (UAV)-aided wireless sensor networks (WSNs), a UAV trajectory planning algorithm named maximum VoI first and successive convex approximation (MVF-SCA) is proposed. First, the Rician channel model is adopted in the system and sensor nodes (SNs) are divided into key nodes and common nodes. Secondly, the data collection problem is formulated as a mixed integer non-linear program (MINLP) problem. The problem is divided into two sub-problems according to the different types of SNs to seek a sub-optimal solution with a low complexity. Finally, the MVF-SCA algorithm for UAV trajectory planning is proposed, which can not only be used for daily data collection in the target area, but also collect time-sensitive abnormal data in time when the exception occurs. Simulation results show that, compared with the existing classic traveling salesman problem (TSP) algorithm and greedy path planning algorithm, the VoI collected by the proposed algorithm can be improved by about 15% to 30%.

Key words：unmanned aerial vehicle; wireless sensor networks; trajectory planning; data collection; value of information

In recent years, wireless sensor networks (WSNs) have been applied in forest monitoring, target tracking, disaster relief, etc. Data collection is one of the most important operations in WSNs. With the development of unmanned aerial vehicles (UAVs), using UAVs in data collection of WSNs has become a hot topic. However, how to efficiently collect data by optimizing the trajectory of UAVs in WSNs is still an open problem which needs further study.

Many approaches have been proposed for data collection in UAV-aided WSNs. These approaches can be classified into two categories. In the first category, Ebrahimi et al.[1-2]proposed the compressive data gathering (CDG) algorithm to compress the data uploaded by the sensor nodes (SNs) to the UAV. A data collection framework was designed to improve data collection efficiency in Refs.[3-4]. In Ref.[5], the balanced network communication protocol (BNCP) was proposed to improve the transmission efficiency during data collection. Zhan et al.[6]jointly optimized the UAV trajectory and node wake-up scheduling to minimize the mission completion time among all UAVs. Zeng et al.[7]jointly optimized the UAV trajectory and the total mission completion time, as well as communication time allocation among SNs to minimize the total UAV energy consumption. Cheng et al.[8]used the traveling salesman problem (TSP) algorithm to plan a traveling path for mobile sinks to reduce the delay time of data gathering. From the perspective of data compression, collection framework, routing protocols, and path planning, these studies enable the UAV to minimize the energy consumption of the UAV or SNs when collecting data. However, the timeliness of the collected data is rarely considered. SNs continuously generate sensing data and the size of the node buffer is limited. If time-sensitive data is not collected in time, it will overflow the buffer and lose its value. In addition, in scenarios such as target tracking, disaster monitoring, and emergency rescues, if the abnormal data can be quickly collected, some actions can be taken to avoid greater losses. Therefore, timely collection of time-sensitive data becomes crucial.

In the second category, some approaches are proposed to collect time-sensitive data. Kaul et al.[9]proposed a metric of age of information (AoI) to measure how new the information is. AoI is defined as the time that has passed since the latest information was generated. Two different AoI indices, namely maximum AoI and average AoI, were proposed in Ref.[10], and dynamic programming (DP) and the genetic algorithm (GA) were used to optimize these two indices. Abd-Elmagid et al.[11-12]studied the long-term weighted sum-AoI minimization problem. In Ref.[13], authors specifically defined the AoI as the time which has elapsed from the moment that the node generates the data packet to the time that the UAV collects the data packet. The outdated packets are minimized in the system through reinforcement learning (RL). As for the time constrained IoT devices, Samir et al.[14]proposed a UAV trajectory planning scheme to maximize the number of served IoT devices. Hu et al.[15]jointly optimized the UAV’s trajectory, the time required for energy harvesting and data collection to minimize the average AoI of the collected data. Li et al.[16]proposed a UAV-aided data collection scheme to minimize the total mission time for emergency applications. Liu et al.[17]proposed a trajectory planning policy to maximize information currency which is measured by the AoI of each sensor node. Similar to the concept of AoI, Turgut et al.[18]put forward a model of the value of information (VoI) and proposed an intruder tracking scheme taking into account the VoI. Bidoki et al.[19]further described the value of information (VoI) which decays with time and proposed a sleep scheduling scheme to maximize the VoI and minimize energy cost. Khan et al.[20]used the metric of VoI in underwater wireless sensor networks and proposed a greedy path planning (GPP) strategy to collect data. In addition, the metric of VoI is also applied to cloud computing resource planning[21]and endangered species monitoring[22].

These VoI related approaches did not consider the time limit of the UAV flight. In this paper, we aim to maximize the VoI of the collected data in a given period for UAV-aided WSNs. The main contributions of this paper are summarized as follows. First, a UAV-aided WSNs model is proposed for data collection under a more practical Rician channel. Based on the model, the data collection problem is formulated as a mixed integer non-linear program (MINLP). Secondly, the formulated problem is divided into two sub-problems according to the node type, and the maximum VoI first and successive convex approximation (MVF-SCA) algorithm for UAV trajectory planning is proposed to maximize the VoI of the collected data within flight time. Finally, a series of simulations are performed and simulation results show that the VoI collected by the proposed algorithm is higher than that of the classic TSP algorithm and the GPP algorithm.

1 System Model

1.1 Network model

In this paper, WSNs are considered for deployment in forest areas for routine data collection and timely warning of unusual events such as fires or illegal biological invasions. The network model is shown in Fig.1, which consists of a series of sensor nodes and a UAV.Msensor nodes are randomly distributed in the target area, which is represented by the setS={1,2,…,M}.iSis used as the index of the node. SNs record the surrounding temperature, humidity and pictures within a collection period. It is assumed that SNs can be divided into two categories according to the collected information. One is the common nodes (CNs), represented by setSc. The data collected by CNs is routine data within the preset normal range with a low degree of emergency. The other is the key nodes (KNs), represented by setSk. The data sensed by KNs is abnormal data, which is not within the preset normal range and has a high degree of emergency,S=Sc∪Sk.

Fig.1 Data collection model in UAV-aided WSNs

The UAV flies above the target monitoring area and collects the data from the SNs. Due to physical limitations, the endurance of the UAV is limited, and the battery needs to be replaced or charged in time when it is low. So, we suppose that the flight time of a collection isT. Assuming that the UAV flies at a fixed altitude ofHmeters above the ground during the collection periodT, the flight trajectory projected by the UAV on the ground can be represented asq(t), 0≤t≤T. DivideTintoNequal time slots withn= 1,2,…,Nas the index, and the length of each slot is denoted asδt. Whenδtis small enough, the position change of the UAV inδtis negligible compared with the distance from the node to the UAV. SinceTis divided intoNtime slots, the trajectoryq(t) can be discretized into a sequence {q[n], 1≤n≤N}, andq[n]R2×1represents the horizontal coordinate of the UAV in time slotn. The initial position and end position of the UAV are denoted byq0andqFR2×1, respectively, which can be determined by specific application scenarios.

The goal of this system is to optimize the trajectory and radio resource allocation of the UAV to maximize the VoI collected within flight timeT. Therefore, the rest of this section introduces the channel model between the UAV and the nodes, the data transmission model and the value of the information model.

1.2 Channel model

In most literature, in order to facilitate optimization, the channel between the UAV and nodes is modeled as a deterministic LoS channel and follows the free space path loss model. However, this simplified model is actually inaccurate in urban and suburban areas, because it ignores random shadowing and small-scale fading. Therefore, our system adopts a more practical Rician channel to model the transmission channel between the UAV and nodes. The channel coefficient between nodeiand the UAV in time slotncan be expressed as

(1)

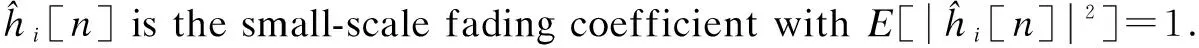
The communication between the UAV and node is shown in Fig.2. Assume that the distance between the UAV and nodeiat time slotnis represented bydi[n], anddi[n] is calculated as

(2)

whereHis the height of the UAV;q[n] denotes the projection coordination of the UAV’s position on the ground;wiis the coordinate of the node.

Fig.2 Communication between the UAV and node

Then, the average channel power gainβi[n] is modeled as

βi[n]=β0di[n]-α

(3)

whereβ0is the average channel power gain when the reference distanced0=1 m, andαrepresents the path loss exponent, which is generally greater than or equal to 2 for the Rician fading channel.

(4)

1.3 Data transmission model

Assuming that nodeiuploads data to the UAV with constant powerP, the received power of the UAV in time slotnis expressed as

Pi[n]=P|hi[n]|2

(5)

Then, the signal-to-noise ratio (SNR)γi[n] of nodeiin time slotnis calculated as

(6)

whereσ2is the noise power. The instantaneous achievable rate ((bit·s-1)/Hz) of nodeiin time slotncan be expressed as

(7)

(8)

1.4 Value of information model

The VoI is a metric originally proposed in game theory which represents the price that the best player is willing to pay for a piece of information. This metric is used in WSN’s latest research and it is a way to assign higher values to recently detected data. The VoI of the sensing data is the highest at the moment of the event, and then decreases with time. Different attenuation models can be used to design VoI functions to meet the requirements of different application scenarios, such as the ramp function, stair function, and exponential function. Ideally, these functions should be constructed based on actual statistical data. In order to maintain generality, this paper uses a decaying exponential function to simulate the VoI functionVi(t).

Vi(t)=Ae-B(t-τ0)

(9)

whereA>0 represents the initial VoI of the node;Bis the decay speed of VoI;τ0is the time of occurrence of abnormal events. The higher the value ofA, the higher the initial VoI of the node, while the greater the value ofB, the faster the attenuation of VoI.

Fig.3 shows the VoI function curves with differentAandB, which can be viewed as three different data emergency levels in WSNs. It can be seen from Fig.3 that events with higherAandBvalues (A2=10,B2=0.3) are more urgent and will expire in about 15 min, while events with lowerAandBvalues (A1=5,B1=0.1) will expire in about 30 min. The data collected by CNs is routine data within the preset normal range with a low degree of emergency, while the data collected by KNs is abnormal data with a high degree of emergency. Therefore, the VoI of KNs can be represented by the VoI attenuation curve, while the VoI unattenuation curve (A3=1,B3=0) can be used to represent the VoI of CNs.

Fig.3 VoI functions with different parameters

2 Problem Formulation

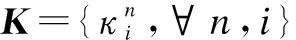
The objective of this paper is to jointly optimize the UAV’s trajectory and radio resource allocation so as to maximize the VoI collected by the UAV within flight timeT. Then, the proposed optimization problem P1 is formulated as

(10)

(10a)

xi∈{0,1}i∈S

(10b)

(10c)

q[n+1]-q[n]≤Dmax∀n≤N-1

(10d)

q[1]=q0,q[N]=qF

(10e)

According to the observation, problem P1 is a mixed integer non-linear program (MINLP), which is NP-hard due to the existence of the binary variablexiand the non-convex constraint (10a). In the next section, the MVF-SCA algorithm is proposed to obtain a sub-optimal solution of problem P1, which is a position sequence that guides the UAV to maximize the collected VoI in the flight period.

3 MVF-SCA Algorithm

As problem P1 proposed in Section 2 is a mixed integer non-convex problem, it is generally difficult to obtain the optimal solution. Therefore, in this paper, our goal is to obtain an efficient sub-optimal solution of P1. First, according to the different node types, problem P1 is divided into two sub-problems. Then, the MVF-SCA algorithm will be proposed to plan the trajectory of the UAV.

The flow chart of the MVF-SCA trajectory planning algorithm is shown in Fig.4. If there is time-sensitive abnormal data in the monitoring area, namely KNs, then the UAV uses the MVF algorithm to fly to the KNs as a priority to collect node data. Otherwise, the UAV uses efficient SCA algorithms for routine data collection. If an area of the UAV is abnormal in the routine data collection process, the node sends a data collection request to the UAV, and the UAV responds to the request, changes the flight path and uses the MVF algorithm to collect abnormal data.

The MVF-SCA algorithm is not only suitable for time-insensitive daily data collection, but also can timely collect time-sensitive abnormal data in the region. Next, the MVF algorithm for collecting the KNs and the SCA algorithm for collecting CNs are described.

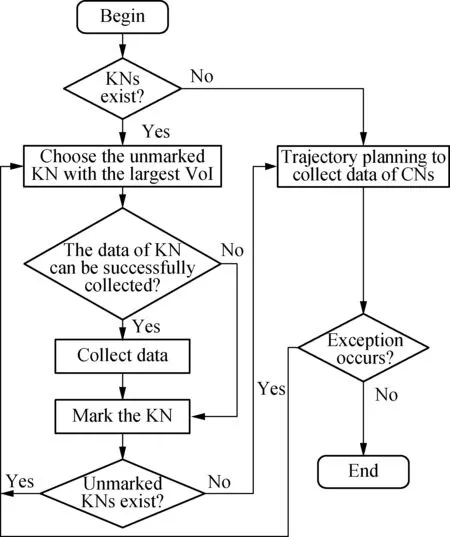
Fig.4 The flow chart of the MVF-SCA algorithm

3.1 MVF algorithm

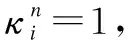
(11)

(11a)

xi∈{0,1}i∈Sk

(11b)

q[n+1]-q[n]≤Dmax∀n≤N-1

(11c)

q[1]=q0,q[N]=qF

(11d)

For the trajectory planning of the UAV collecting KNs, we propose the MVF algorithm, which allows the UAV to plan the trajectory according to the VoI of KNs, giving priority to the node with the largest VoI. Among all the KNs that need to be collected, the UAV will first collect the node with the largest VoI in the uncollected node. If the UAV can arrive at the node and collect enough data in the rest time slot, then the UAV will fly to the node to collect data; otherwise, the UAV will select another node from the unmarked nodes and carry out a similar process. The pseudo-code of the MVF algorithm is shown as follows.

Algorithm1The MVF algorithm for collecting data of KNs

Input:q0,vmax,Smin,T,δt; the location of all KNs; the initial VoI of all KNs.

Sort all KNs based on their initial VoI.

Calculate the distance from the KN to the current location of the UAVdU2N

Set the number of time slotsN←T/δt

Set the updated timeN′←N

foriSkdo

Select the node with the highest VoI among unmarked nodes

Find the minimum time to collect the KN and update the flying timeN′

Update the location of the UAV

else

Mark the KN and update the flying timeN′

end if

end for

Output: The trajectory for the UAV collecting the data of KNs.

3.2 SCA algorithm

Next, the collection of CNs will be considered. Since the VoI of CNs is a constant, maximizing the VoI of CNs is to maximize the number of collections of CNs withinT. Therefore, the sub-problem P3 can be specifically expressed as

(12)

(12a)

xi∈{0,1}i∈Sc

(12b)

(12c)

q[n+1]-q[n]≤Dmaxn≤N-1 (12d)

q[1]=q0,q[N]=qF

(12e)

(q[n]-wi2-qr[n]-wi2)

(13)

where

(14)

(15)

(16)

Then, problem P3 can be rephrased as problem P4 as follows:

(17)

(17a)

(17b)

(17c)

0≤xi≤1i∈Sc

(17d)

(17e)

(17f)

q[n+1]-q[n]≤Dmax∀n≤N-1

(17g)

q[1]=q0,q[N]=qF

(17h)

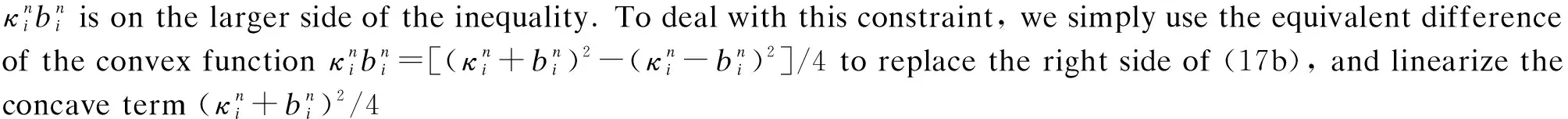
(18)

Algorithm2SCA algorithm for collecting data of CNs

Input:Smin; the error toleranceε.

While (Obj(r-1)-Obj(r))>εdo

Solve the convex problem P4 by interior-point solvers to obtain the trajectoryqr+1[n], ∀n,

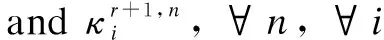
Update the trajectory of the UAV

Update the resource allocation

r←r+1

End while

Output: The trajectory for the UAV collecting the data of CNs.

4 Performance Evaluation

4.1 Simulation environment

We assume that SNs are randomly distributed in the target region and the scale of the target region is 500 m×500 m. The CVX toolbox and the numerical convex solver SDPT3 are used to solve our optimization problem. We set the initial and final positions of the UAV to the center of the target area ([250, 250]). The algorithm is run in Windows 10 with a CPU i7-6700. Details of the parameters in the simulation are listed in Tab.1.

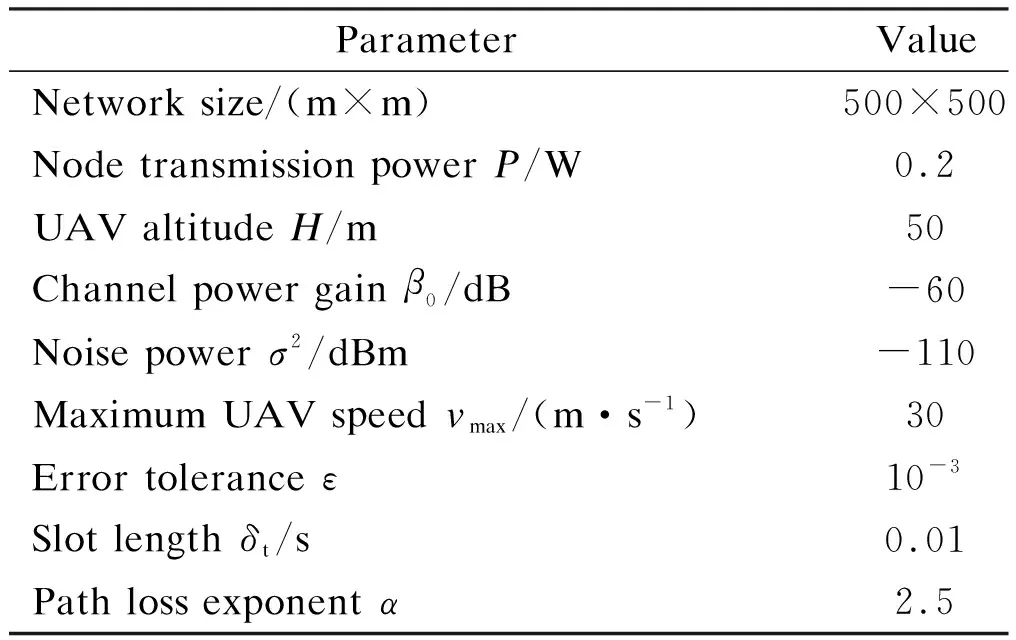
Tab.1 Parameters for simulations

4.2 Performance evaluation

4.2.1 Complexity analysis

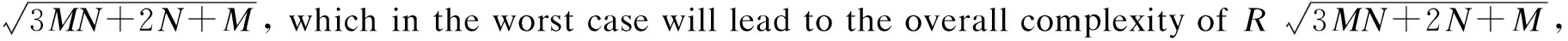
4.2.2 Trajectory planning

The trajectory of the UAV planned by the MVF-SCA algorithm is shown in Fig.5. There are 4 KNs and 16 CNs in the network. The UAV starts from the central point of the monitoring area [250,250] and returns after a collection periodT. In order to maximize the total VoI collected, the UAV first collects the KNs represented by the red asterisk mark. The UAV adjusts the trajectory to collect the most urgent KNs. When collecting CNs represented by the green dots marks, the UAV can allocate radio resources to collect multiple nodes in the same time slot. The black cross mark represents the node that has not been collected by the UAV or that has not uploaded the minimum amount of data in the collection periodT.

Fig.5 UAV trajectory planning by the MVF-SCA algorithm

4.2.3 Data collection

The performance of the proposed MVF-SCA algorithm is compared with that of the classical TSP algorithm[8]and the GPP algorithm[20]. Fig.6 shows the change of VoI collected by the UAV in collection periodTas the number of network nodes increases. In the simulation, we maintained that KNs accounted for 20% of the total SNs. The increase in the number of nodes leads to the increase in the density of network nodes, which will help the UAV to collect more nodes inTand obtain a greater VoI. The MVF-SCA algorithm proposed has an improvement of about 15% compared with the TSP algorithm, and an improvement of about 30% compared with the GPP algorithm.

Fig.6 The comparison of collected VoI by different algorithms

Finally, the effect of the minimum data amountSminon the performance of different algorithms is studied. As shown in Fig.7, whenSmin=0 Mbit, there is no requirement for the amount of data uploaded by the node. As long as the UAV collects data greater than 0 bit at the node to obtain the VoI of the node, the VoI collected by the UAV is the largest. AsSminincreases, the total VoI collected during the flight timeTof the proposed MVF-SCA algorithm, GPP algorithm and TSP algorithm has decreased by varying degrees. AsSminbecomes larger, the time for the UAV to collect a node becomes longer, so that the number of nodes collected within the limited flight timeTdecreases, and the VoI of the collected data decreases accordingly. The proposed MVF-SCA algorithm is always better than the GPP algorithm and TSP algorithm for the sameSmincollection performance, because the MVF-SCA algorithm jointly optimizes the UAV trajectory and radio resource allocation for different attributes of the nodes.

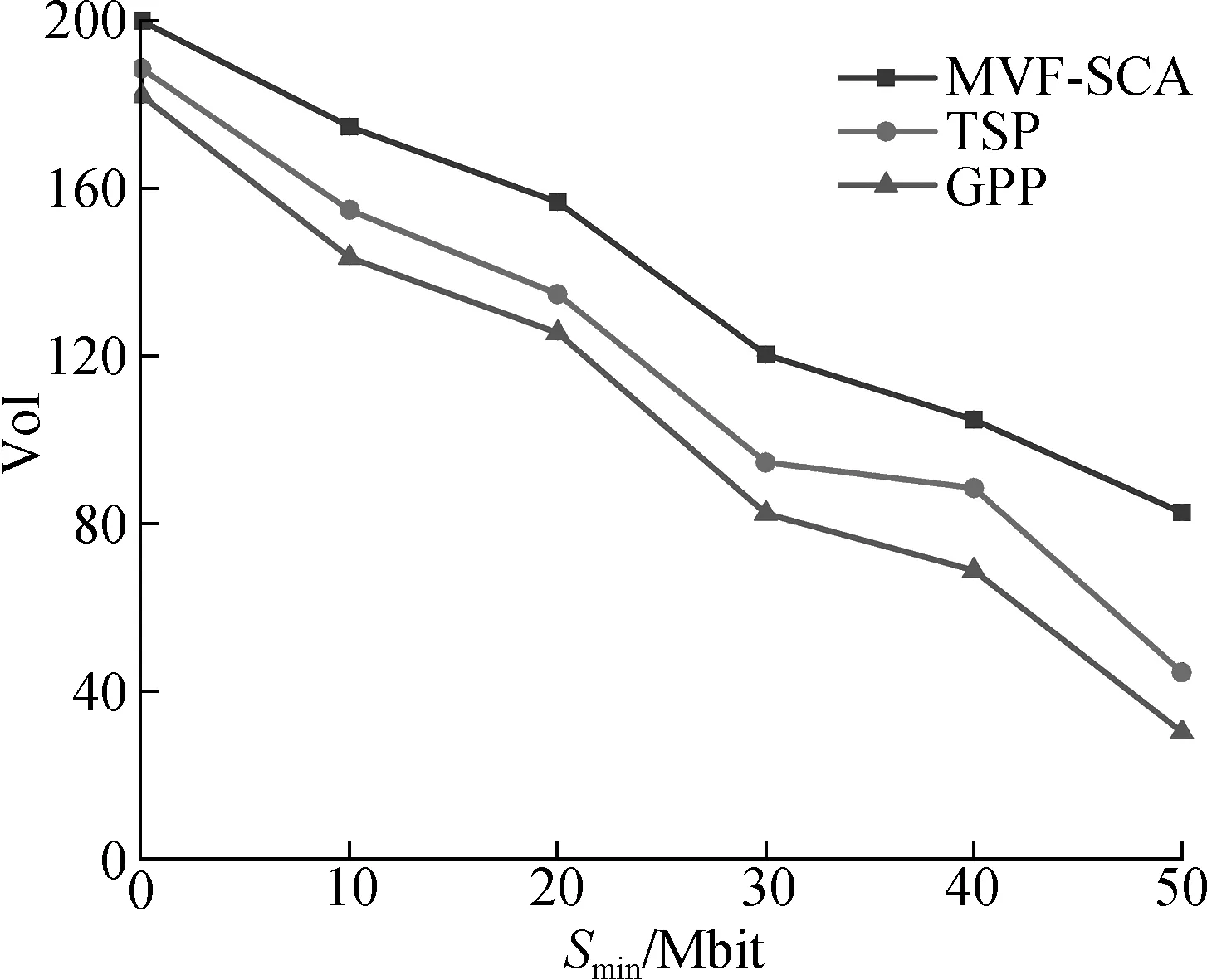
Fig.7 The collected VoI vs. the minimum data amount Smin

5 Conclusions

1) The data collection problem in UAV-aided WSNs is investigated in this paper. The Rician model and the concept of VoI are considered.

2) The problem is formulated as a mixed integer non-linear program problem which is non-convex. The problem is then transferred to two sub-problems according to the node type. A UAV trajectory planning algorithm is proposed to solve the two problems.

3) Simulation results show that the VoI collected by the proposed algorithm can improve by 15% to 30% compared with the classical TSP algorithm and the GPP algorithm.