Q-learning-based energy transmission scheduling over a fading channel
2021-01-12WangZhiweiWangJunboYangFanLinMin
Wang Zhiwei Wang Junbo Yang Fan Lin Min
(1 School of Cyber Science and Engineering, Southeast University, Nanjing 210096, China)(2 School of Information Science and Engineering, Southeast University, Nanjing 210096, China)(3 School of Science, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)
Abstract:To solve the problem of energy transmission in the Internet of Things (IoTs), an energy transmission schedule over a Rayleigh fading channel in the energy harvesting system (EHS) with a dedicated energy source (ES) is considered. According to the channel state information (CSI) and the battery state, the charging duration of the battery is determined to jointly minimize the energy consumption of ES, the battery’s deficit charges and overcharges during energy transmission. Then, the joint optimization problem is formulated using the weighted sum method. Using the ideas from the Q-learning algorithm, a Q-learning-based energy scheduling algorithm is proposed to solve this problem. Then, the Q-learning-based energy scheduling algorithm is compared with a constant strategy and an on-demand dynamic strategy in energy consumption, the battery’s deficit charges and the battery’s overcharges. The simulation results show that the proposed Q-learning-based energy scheduling algorithm can effectively improve the system stability in terms of the battery’s deficit charges and overcharges.
Key words:energy harvesting; channel state information; Q-learning; transmission scheduling
With the rapid development of the IoTs, energy harvesting has been regarded as a favorable supplement to drive the numerous sensors in the emerging IoT[1]. Due to several key advantages such as being pollution free, having a long lifetime, and energy self-sustainability, the energy harvesting systems (EHSs) are competitive in a wide spectrum of applications[2].
The EHS generally consists of an antenna either separating or shared with data communications, an energy harvesting device (EHD) converting the RF signal from energy sources (ESs) to power, and a battery that stores the harvested energy[3]. According to different ESs, the RF-based energy harvesting system can be classified into two categories: EHS with ambient ESs and EHS with a dedicated ES[3].
Recent research of the EHS mainly focuses on how to effectively utilize energy from ambient or dedicated ESs[4-6]. In Ref.[4], an energy neutrality theorem for EHN was proposed and it was proved that perpetual operation can be achieved by maintaining the energy neutrality of EHN. Then, an adaptive duty cycle (ADC) control method was further proposed in order to assign the duty cycle online to achieve the perpetual operation of EHN. In Ref.[5], a reinforcement learning-based energy management scheme was proposed to achieve the sustainable operation of EHN. In Ref.[6], a fuzzyQ-leaning-based power management scheme was proposed for EHN under energy neutrality criteria. To achieve the sustainable operation of EHN, the duty cycle is decided from the fuzzy inference system for the EHN. In fact, all the research managed to adjust power in the EHS with ambient ESs to maximize the utilization of the harvested energy. However, due to the lack of the contact between the ESs and EHDs, the energy transmission period in the EHS with ambient ESs are more uncontrollable and unstable. However, in the EHS with a dedicated ES, the progress of energy transmission can be scheduled effectively due to the dedicated ES which is installed to power the EHDs. Hence, some research began to focus on the EHS with a dedicated ES. In Ref.[3], a two-step dual tunnel energy requesting (DTER) strategy was proposed to minimize the energy consumption at both the EHD and the ES on timely data transmission. However, these existing strategies did not consider the exhaustion or overflow of the battery’s energy during the transmission. Hence, this paper will concentrate on the online energy management strategies to improve system stability in terms of the battery’s deficit charges and overcharges.
In this paper, aQ-learning-based energy transmission scheduling algorithm is proposed to improve the EHS with a dedicated ES. Based on the basic theories of theQ-learning algorithm[7], an energy transmission scheduling algorithm is used to decrease energy consumption through adjusting transmitted energy. By using the energy scheduling scheme in this paper, the EHS can adjust the transmitted energy of ES timely and effectively to change the energy consumption. First, the system model of the EHS is presented in detail. Then, a multi-objective optimization problem is formulated to improve system performance in terms of the battery’s deficit charges and overcharges. Next, aQ-learning-based scheduling algorithm is proposed for the optimization problem. Finally, the simulation results and conclusions are presented, respectively.
1 System Model
Consider an RF-based EHS, where the EHD requests and harvests energy from the ES, as shown in Fig.1. The harvested energy stored in the EHD’s battery is consumed to send out data. Moreover, the system time is assumed to be equally divided intoNtime slots andTn(1≤n≤N), the duration of time slotnis constant and selected to be less than the channel coherence time. Therefore, the channel states remain invariant over each time slot but vary across successive time slots. Assume that the fading of the wireless channel follows a correlated Rayleigh fading channel model[8]. Using the ellipsoidal approximation, the CSI can be deterministically modeled as[9]
gn=hn10-vn/10
(1)
wherevnis the uncertain parameter andθdenotes the uncertainty bound which is a non-negative constant;gnandhndenote the actual and estimated channel gains at time slotn, respectively.
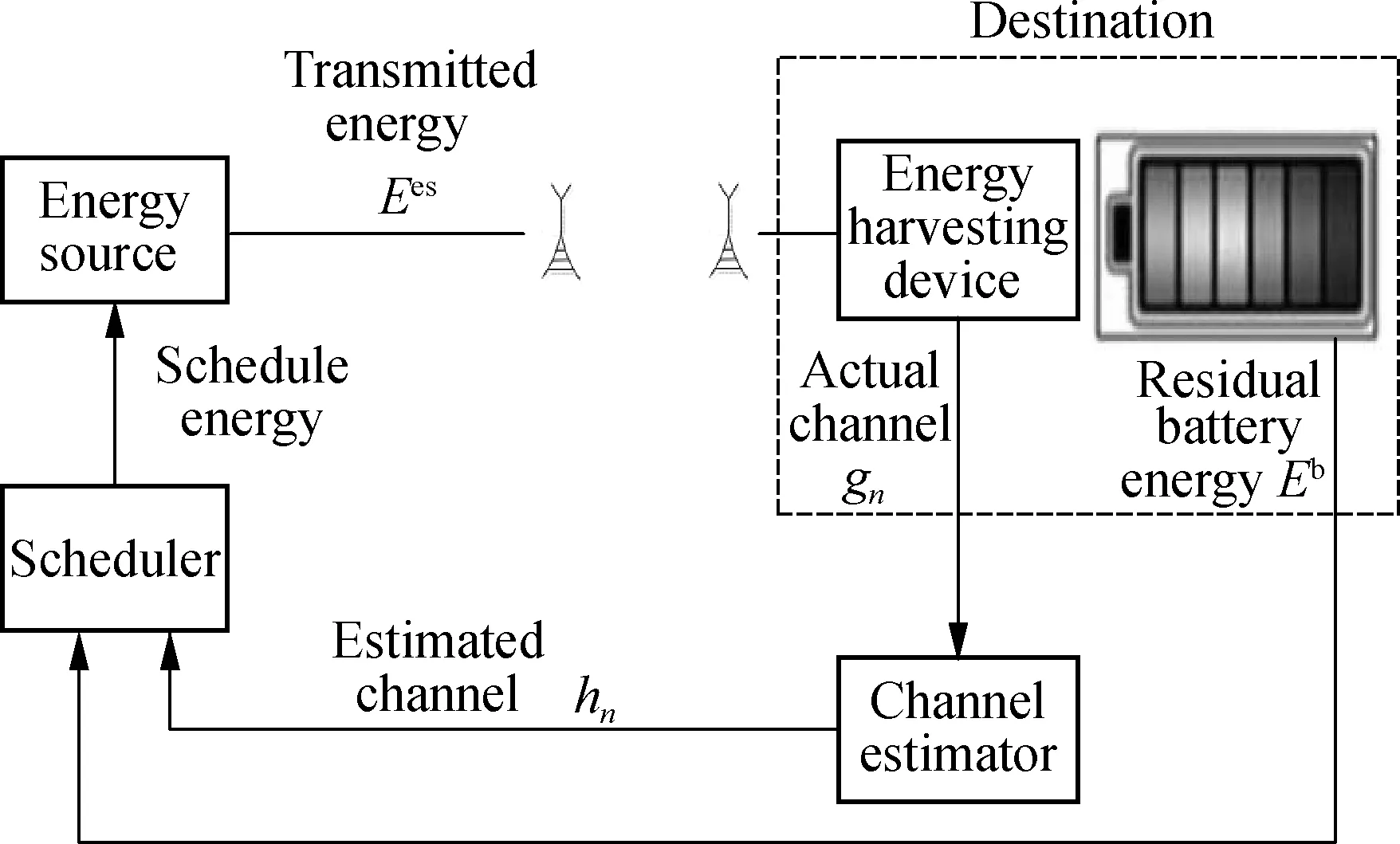
Fig.1 The energy-harvesting system
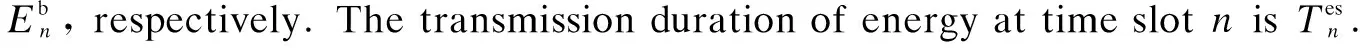
Vn=Vm(1-e-t′/(RC))
(2)
(3)
(4)
(5)
wheret′ is the time consumed during charging the voltage of the battery from 0 toVnwithVmvolts of voltage;Vmis the maximum voltage that the battery can approach.RandCare the resistance and capacitance of the charging circuit in EHD, respectively. Eq.(2) represents that the battery needs to spend timet′ on voltage changing from 0 toVnand Eq.(3) represents that the voltage changes fromVntoVn+ΔVnafter energy harvest at time slotn. Eq.(4) and Eq.(5) reflect the relationship between the battery’s voltage and stored energy. Using Eq.(2) to Eq.(5), the charge duration can be derived as
(6)
(7)
wherepthdenotes the charge power of a battery.
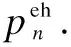
(8)
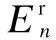
(9)
whereηrepresents the conversion efficiency of a battery.
2 Problem Formulation
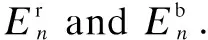
(10)
whereυrepresents the minimum capacity percentage of the battery that can keep EHD normally. Meanwhile, due to the limitation of the storage size, the overflow of the battery’s energy will occur when the received energy is too large. Therefore, how to avoid overcharges of the battery should be taken into account as well. The condition of the battery’s overcharge at time slotncan be described as
(11)
In most cases, it is unlikely that the three objectives can simultaneously be optimized by the same solution. Therefore, some tradeoff between the above three objectives is needed to ensure satisfactory system performance. The most well-known tradeoff method is the weighted sum method[11]. Accordingly, the multi-objective optimization problem can be converted into the following minimization problem,
(12)
whereE(·) is the expectation operator;I(·) is an indicator function and is used to show the occurrence of overcharges or deficit charges;τandμare two small positive constants, which are used to adjust the weight of deficit charges and overcharges of the battery during the optimization.
3 Online Scheduling Algorithm
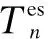
3.1 State
Channel state and residual battery energy are continuous variables, which should be converted into discrete and finite. Therefore, we divided the ranges of the continuous variable into several intervals. If different variables are located in the same interval, they are regarded the same. To distinguish these intervals, we use continuous natural numbers to label them and these numbers can be regarded as different states.
In the proposed scheduling scheme, the channel states are assumed to be discrete and finite.Without loss of generality, the range of the estimated channel gain can be divided intoDstates. The states can be defined as
(13)
where 0<ω1<ω2<…<ωD-1. Therefore, at time slotn, the channel state can be determined as
(14)
Similarly, the residual battery energy, which is also assumed to be discrete and finite, can be divided intoEstates as follows:
(15)
(16)
Using the residual energy and channel states, the current composite state of the system is defined in a vector as
Sn={Hn,En}{1,2,3,…,D}×{1,2,3,…,E}
(17)
Eq.(17) represents that every state can be mapped into the only combination ofHnandEn.
3.2 Action
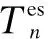
(18)
3.3 Cost
In the optimization problem Eq.(12), the objective is to save energy consumption, avoid overflow of a battery’s energy and prevent a battery from draining. Therefore, the total cost is determined as
(19)
As different circumstances have different QoS requirements, by adjustingμandτ, the reward function is generic enough to satisfy different requirements in real systems.
3.4 Action selection
Using the states, actions and cost functions defined above, the received energy at time slotncan be selected by
(20)
After selecting the proper action, the next state of battery energyEn+1can be determined by Eq.(8) and Eq.(16). Also, the next channel stateHn+1can be obtained by Eq.(14). Hence, combined with the information ofEn+1andHn+1, the next stateSn+1is determined as well. Accordingly, matrixQwill be updated as
(21)
whereαis the time-varying learning rate parameter;γis the discount factor. The detailed procedures of the algorithm are shown in Algorithm 1.
Algorithm1The Q-learning-based scheduling algorithm
Step1Initialization.
Step2If rand()<ε, randomly select an action fromAn. Else, select an action using Eq.(19).
Step3Calculate the cost using Eq.(18) and then determine next stateSn+1.
Step4UpdateQby Eq.(20).
Step5n=n+1 , then go to step 2.
4 Simulation and Results
Under the same simulation environments, the proposed algorithm is compared with the constant strategy algorithm and the on-demand dynamic strategy algorithm[3]in terms of the battery’s deficit charges, the battery’s overcharges and the total consumed energy. The proposed algorithm and the reference algorithms are, respectively, deployed at most 100 times in one trial, and the trial is repeated 1 000 times. In other words, the ES transmits energy to EHD in each trial, which will not stop unless the battery’s energy is exhausted or transmission is carried out more than 100 times. After trials are completed, the data from simulations will be collected to analyze the performance of the algorithms.
4.1 Simulation settings
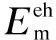
4.2 Performance comparison
For comparison purpose, the reference algorithms are described as follows.
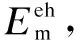
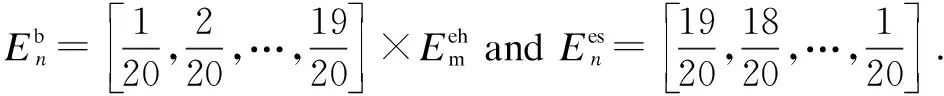
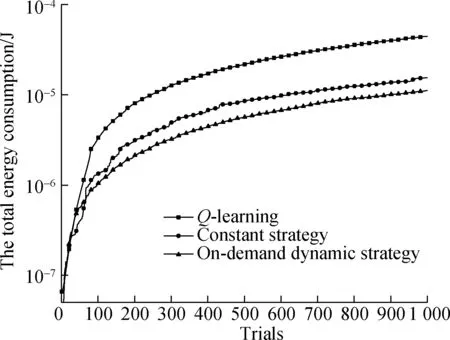
Fig.2 shows the performance comparison between the proposedQ-learning algorithm and reference algorithms. In Fig.2(a), it is noted that theQ-learning algorithm achieves an excellent performance in terms of the battery’s deficit charges. As the reference algorithms do not consider the effect of the battery’s deficit charges, the battery’s energy cannot be prevented from becoming exhausted during trials and the occurrence of the battery’s deficit charges increases with the trials’ continuation. In Fig.2(b), the preference algorithms outperform theQ-learning algorithm slightly in the overcharges. The reason is that both the constant strategy and on-demand strategy algorithms have considered the restriction of overcharges so that the overflow of the battery’s energy never occurs during trials. In Fig.2(c), both the reference algorithms consume less energy than theQ-learning algorithm, but this consequence is based on the degradation in its performance of the battery’s deficit charges. To sum up, although theQ-learning algorithm seems to consume more energy than the reference algorithms, it actually provides better system stability during the energy transmission period.
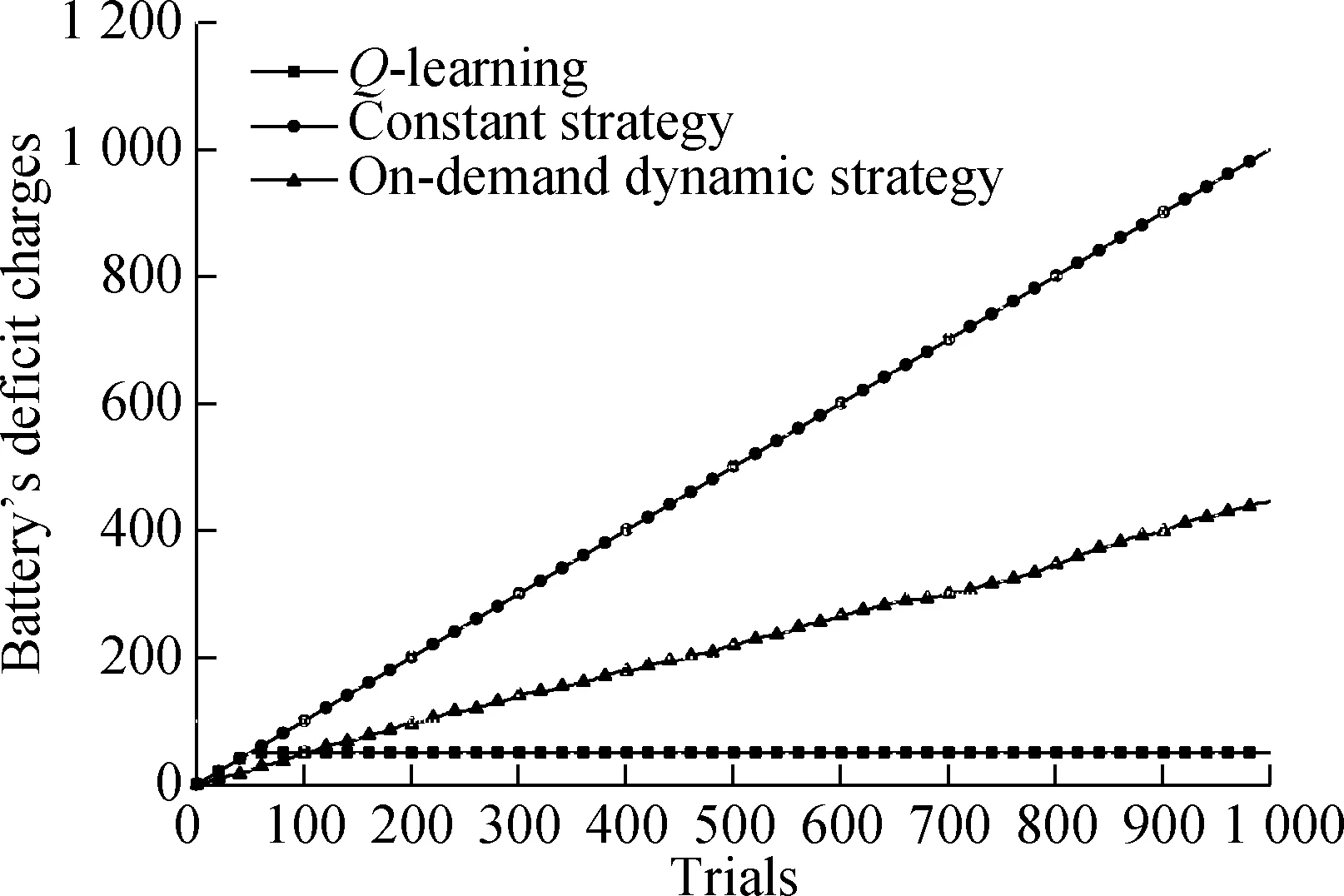
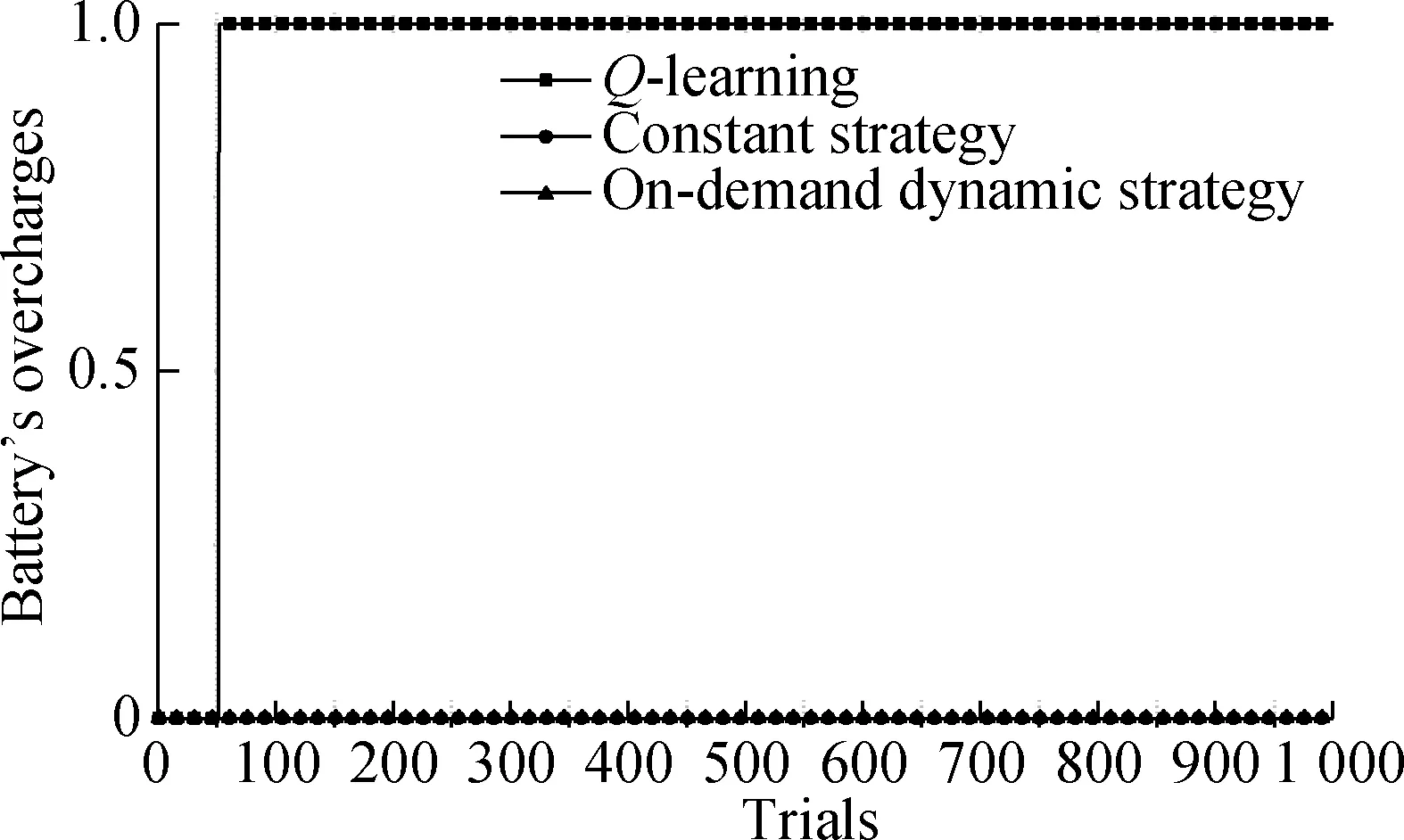
For theQ-learning algorithm, the size of action space can be an important factor that influences algorithm performance. To verify how action space size affects algorithm performance, the simulations of theQ-learning algorithm with different action space sizes are executed under the same simulation environment. The results are shown in Fig.3.
(a)
(b)
(c)
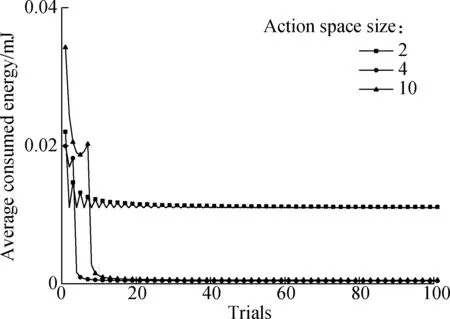
Fig.3 The averaged energy consumption of the Q-learning algorithms with different sizes of action space
Assume that the size of state space is kept at 10 during simulations. It can be seen that a large action space will result in longer convergence time[12], which is also demonstrated in Fig.3. Through the accumulated information of multiple iterations, the information of CSI will be obtained. In other words, theQ-learning algorithm spends time in learning before the first 20 trials. In the practical, for the first 20 trials, the system is in the progress of learning, and thus the derived results are not optimal. After the first 20 trials of learning, the system can grasp the best strategy of all the states and the averaged energy consumption of the ES converges to a constant value. In addition, the action space never becomes as large as possible. If the action space is large enough to obtain the optimal averaged energy consumption, a larger action space will only extend the convergence time without reducing energy consumption.
5 Conclusions
1) The proposedQ-learning algorithm can solve the proposed issue and achieves acceptable system performance over different Rayleigh fading channels in terms of energy consumption, a battery’s deficit charges and overcharges.
2) Compared with the two reference algorithms, theQ-learning algorithm shows a significant advantage in avoiding a battery’s energy from becoming exhausted. From the practical view, it is worthwhile to sacrifice performance in energy consumption in exchange for better system stability.
3) The size of action space can affect theQ-learning algorithm’s performance. A small action space causes a shorter convergence time, but cannot converge to the optimal solution. In fact, theQ-learning algorithm with a larger action space can effectively reduce energy consumption during a long time energy transmission.
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Bandwidth-enhanced dual-polarized antenna with improvedbroadband integrated balun and distributed parasitic element
- UAV trajectory planning algorithmfor data collection in wireless sensor networks
- A multi-attention RNN-based relation linking approach for question answering over knowledge base
- Time optimization for workflow scheduling based on the combination of task attributes
- Centre symmetric quadruple pattern-based illumination invariant measure
- Flexural behaviour of SFRRAC two-way composite slab with different shapes
