Flexural behaviour of SFRRAC two-way composite slab with different shapes

Luo Bin Huang Wei

(1School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China) (2School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract：To promote the application of green renewable materials in concrete composite slabs (CCSs) and study the flexural behavior of CCSs with different shapes, the bending performances of three CCSs with a SFRRAC base plate, one cast-in-site concrete slab of ordinary concrete and one CCS of ordinary concrete by steel bar truss (as recommended in the technical specification for precast concrete structures in Chinese) were compared through experiments. The carrying capacity, flexural behaviour and bi-directional mechanical properties of the specimens were systematically analyzed from the failure modes, load-deflection curves, load-bar strain curves, load-slip curves and crack distributions. Results show that the bending failure process of CCSs with a SFRRAC base plate is similar to that of the cast-in-site concrete slab of ordinary concrete and CCS of ordinary concrete by steel bar truss, as all of them went through the plastic phase, elastic plastic phase and failure phase with fully developed cracks and deflection. No sudden breakage or horizontal cracking of the connecting interface between the base plate and concrete topping was observed. The shape of the base plate has a major impact on the bearing capacity of the CCS with the SFRRAC base plate. When calculating the ultimate bearing capacity with the plastic yield line theory, the influence of the base plate shape on the plastic yield line position should be taken into account.

Key words：concrete composite slab (CCS); shape; steel bar truss; bending performance; ultimate bearing capacity

The precast concrete structure has the advantages of being labour-saving, energy-efficient and having low-carbon features[1]. It will be widely used in residential construction. One of the key components of this structure is the concrete composite slab (CCS), which supports the fast construction of solid buildings with a few templates[2-4]. With the proliferation of the precast concrete structure, the CCS has been widely applied in residential construction across China and elsewhere in the world.

Much theoretical research has been done on the design, production and construction of the CCS, yielding various CSSs that are easy to transport and install. For instance, Mohammed et al.[5-6]developed a CCS by adopting crumb rubber fine aggregates in the concrete topping, creating a solution for the disposal of waste tires. Majdi et al.[7]put forward a CSS with a bottom of cold-formed steel profiles, corrugated steel decks, a concrete topping and furring channels, which maximizes the advantages and minimizes the disadvantages of steel and concrete. An et al.[8]proposed an innovative cable supported beam structure-concrete slab composite floor. Kim et al.[9]designed a CCS with concrete, steel bars, perfobond rib shear connectors, and profiled steel sheets vertical to the girder, aiming to create a large interior space required for public buildings and bridges. Ueda et al.[10-11]presented several types of precast hollow CCSs to overcome the heavy weight and transportation difficulty of the ferrocement-brick composite slab created by Thanoon et al[12]. Carbonari et al.[13-15]proposed precast concrete sandwich panels in different forms and with different materials, in an attempt to preserve the heat and integrate the load bearing capacities of precast components; and the feasibility of these panels were verified through calculation by Benayoune’s theory[16]. All of the above studies have contributed greatly to the development of the CSS and reflect the local conditions of various application scenarios.

The rapid urbanization in China is accompanied by an upsurge in the amount of construction wastes (about 30% to 40% of urban wastes), posing a serious threat to ecological environments[17]. To mitigate the threat, a viable option lies in the preparation of green concrete through recycling of the huge amount of construction wastes[18]. In this way, it is possible to produce recycled aggregate concrete from recycled aggregates instead of natural aggregates, and apply it in the industrial production of precast concrete structure components like the CCS. This approach will relieve the excessive consumption of concrete, reduce the pollution from construction wastes, and match with the trend of construction industrialization and green buildings.

Nevertheless, ordinary aggregate concrete is often outperformed by the recycled aggregate concretes, owing to the latter’s low apparent density, internal micro-cracks and high crush index, leading to a limited application for engineering[19]. In previous studies, our research groups have introduced steel fibres into recycled aggregate concrete to enhance the apparent density and reduce internal micro-cracks creating the steel fibre-reinforced recycled aggregate concrete (SFRRAC)[20], and proved that the steel fibres can effectively prevent the micro-crack development and improve the mechanical performance of recycled aggregate concrete.

Inspired by the research results on the SFRRAC, this paper combines the SFRRAC base plates of three different shapes with cast-in-situ concrete topping into CCSs, with the aim to developing CCSs with excellent mechanical properties. Five full-scale specimens were produced, including three SFRRAC CCSs of different shapes, one cast-in-situ concrete slab, and one ordinary concrete CCS reinforced by steel bar truss according to the Chinese technical specification JGJ 1—2014[21]. Finally, the authors derived the calculation formula of the ultimate bearing capacity of the SFRRAC CCSs.

1 Experimental Program

1.1 Details of specimens

Five specimens, denoted as S1 to S5, were designed according to the dimensions and parameters in Tab.1 and Fig.1(a), of which S1 and S2 are control specimens. S1 is the cast-in-site concrete specimen, and S2 to S5 are CCS specimens. S2 to S5 consist of a precast base plate and a cast-in-site concrete topping. S2 to S5 share the same topping (ordinary concrete) and differ in the precast base plate. S2 has ordinary concrete base plates, while S3 to S5 have SFRRAC base plates. In Tab.1,Lis the span of the specimen,Wis the width of the specimen,tbis the thickness of precast panel, andttis the thickness of cast-in-site concrete topping (or the thickness of cast-in-site).

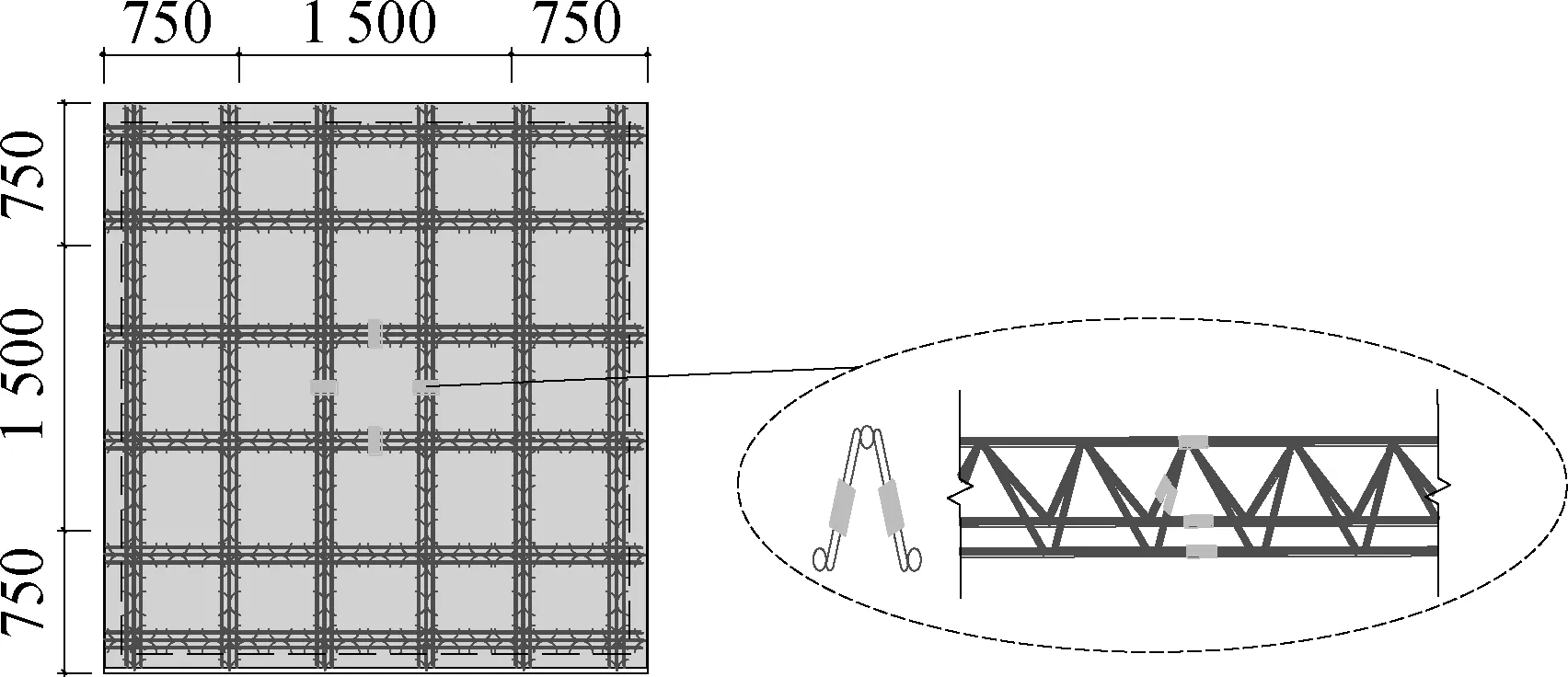
In addition, the precast base plates of the five specimens were equipped with two-way (i.e.X-/Y- direction) reinforcements, which adopted eight hot rolled ribbed barsD8 (diameter 8 mm) spaced at 150 mm (D8@150). In order to prevent cracking during hoisting, 6 mm-diameter hot rolled plan barsD6 spaced at 250 mm (D6@250) used as transverse reinforcement were arranged on the top of all specimens. Meanwhile, the A90 type steel bar truss was used for theY-direction of four precast base plates of S2, S3, S4, S5, and the A70 type steel bar truss was used for theX-direction of precast base plate of S4. Details of specimens reinforcement are shown in Fig.1(b).

(a)

(b)

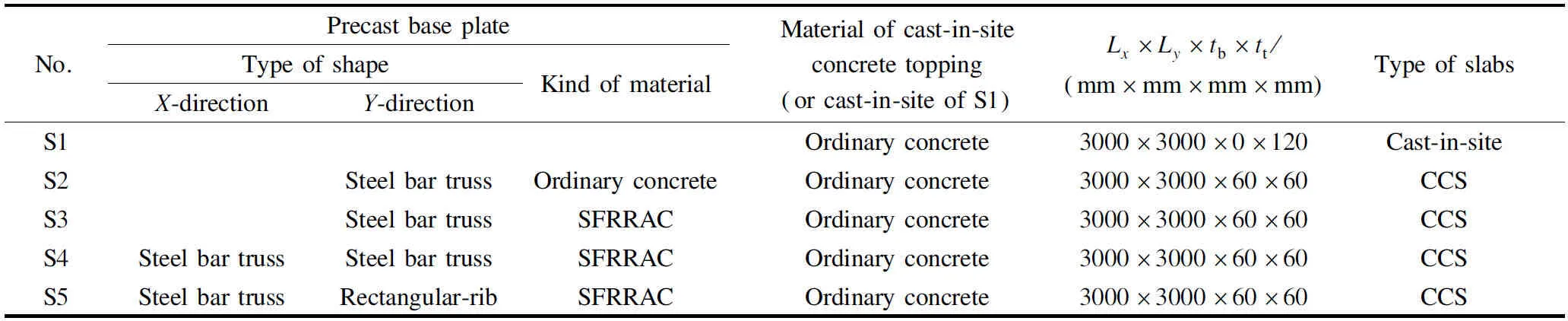
Table.1 Basic parameters of specimens

1.2 Properties of specimens

According to the our previous research[20], the raw materials of the SFRRAC precast base plates were selected: All coarse aggregates were crushed and screened waste concretes; the fine aggregates were natural sand; the steel fibres (volume fraction 1%; length 35 mm; diameter 0.56 mm; tensile strength 2 300 MPa) were shear-pattern steel fibres.

Three cubes (side length 150 mm) and three prisms (L×W×H=150 mm×150 mm×300 mm) were prepared for each specimen to measure the actual cubic compressive strength, splitting tensile strength and axial compressive strength (see Tab.2)[22]. The mechanical properties of the reinforcements are listed in Tab.3.

Table.2 Mechanical properties of concretes

Table.3 Mechanical properties of reinforcement

1.3 Fabrication process of specimens

Each of the four CCS specimens was fabricated in two stages. As shown in Fig.2(a), the precast base plate was produced through mould fixing, brushing of the release agent, bar bindings, concrete pouring, and surface roughening. As shown in Fig.2(b), the cast-in-site concrete topping was fabricated after the concrete strength of the base plate reached 100% through the following steps: mould fixing, bar bindings, and concrete pouring.

(a)

(b)

1.4 Test setup and procedure

During the experiment, the load was applied manually via a 1 000 kN hydraulic actuator. Each slab was simply supported on four sides and subjected to the load at eight points in theY-direction and four points in theX-direction. All points were under the same load, creating a homogenous loading pattern. The force generated by the hydraulic pump was transferred from the jack to the specimen via rigid girders. To prevent punching failure, a square steel pad with a side length of 200 mm was placed under the second rigid girder, and covered with sand at its bottom. The experimental set-up is shown in Fig.3.

1—sensor;2—jack;3—first stage distribution beam;4—second stage distribution beam;5—third stage distribution beam;6—steel pad;7—support;8—specimen’s bracket;9—LVDTs(a)

(b)

According to the Chinese standard GB/T 50152—2012[23], the loading process was divided into pre-loading and formal loading. In pre-loading, there were three loading phases and three unloading phases, each of which had a load increment of 5 kN. In formal loading, the load increment was initially 5 kN per phase, adjusted to 10 kN per phase after the cracking of the specimen, and changed back to 5 kN per phase when the load reached 90% of the calculated ultimate bearing capacity. After each load increment, the mid-span deflection, strain and crack propagation pattern were recorded for further analysis.

It is considered that the specimen has reached the limit state of bearing capacity and stopped loading[23], when the specimen reaches one of the following conditions: The midspan deflection reaches 1/50 of the full span, the crack width of the slab bottom concrete widens to 1.50 mm, the strain of steel bar reaches 0.01, and the concrete is crushed in the compressive zone or the fracture of tension reinforcement.

1.5 Measurements

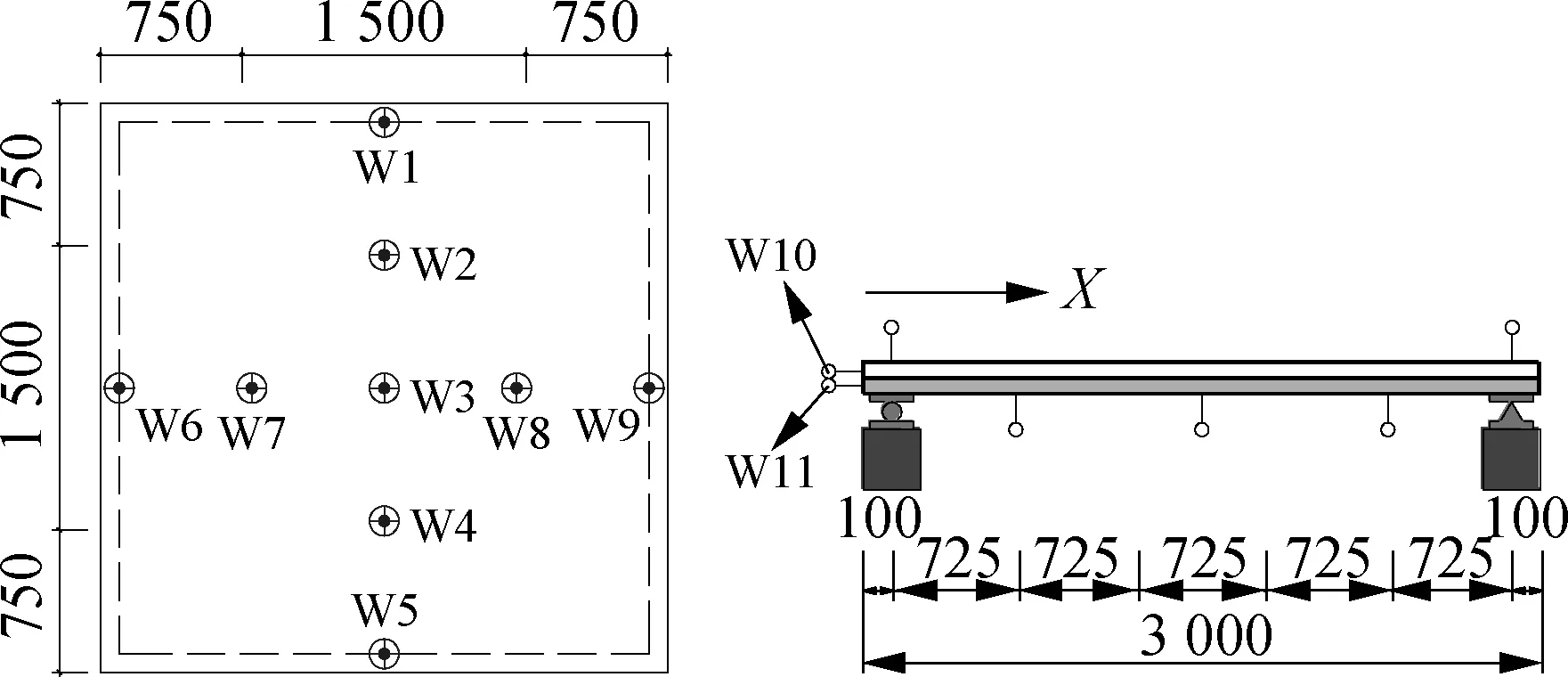
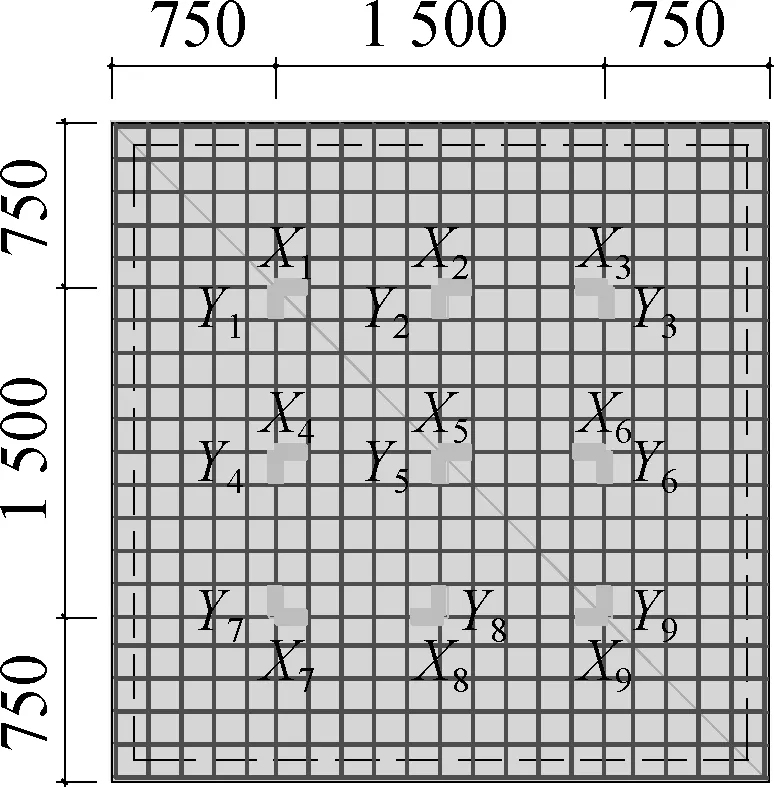
The vertical load was measured by the force sensor in Fig.4(a). A total of five linear variable displacement transducers (LVDTs) were placed at the bottom of each specimen to measure the bending deflection in two directions(i.e. W2, W3, W4, W7, and W8), and four LVDTs were placed at the top of each specimen(i.e. W1, W5, W6, W9). Two LVDTs were arranged, respectively, at the two ends of the precast base plate and concrete topping to record the interface slip(i.e. W10 and W11). As shown in Fig.4(b), eighteen bar strain gauges were installed on the compressive bar inX-directions (i.e.X1toX9) andY-directions (i.e.Y1toY9) on specimen bottom. A steel bar strain gauge was provided at the upper/ lower chords and web of the bar closest to the slab centre of the steel bar truss in specimens(S2 to S5).

(a)

(b)

(c)

1.6 Characteristic load determination method

The cracking load was determined in three ways: Firstly, when the first crack appears in the loading process, the corresponding load should be taken as the cracking load; secondly, when the first crack appears in a specific loading phase, the mean load between the current phase and the previous phase should be taken as the cracking load; thirdly, when the first crack appears after a specific loading phase, the current load should be taken as the cracking load[23].

The yield load of a member was determined by the farthest point method[24], that is, the yield load of a member should be measured at the yield point whose tangent slope is the same as the connecting line between the origin and the ultimate loading point. The yield point determination is detailed in Fig.5. The calculation method of the yield point load is shown as

(1)

where (F,D) is the component of the force-deformation curve; (Fys,Dys) is the yield point coordinate obtained by the farthest point method; and (Fp,Dp) is the peak point coordinate (0≤D≤Dp).

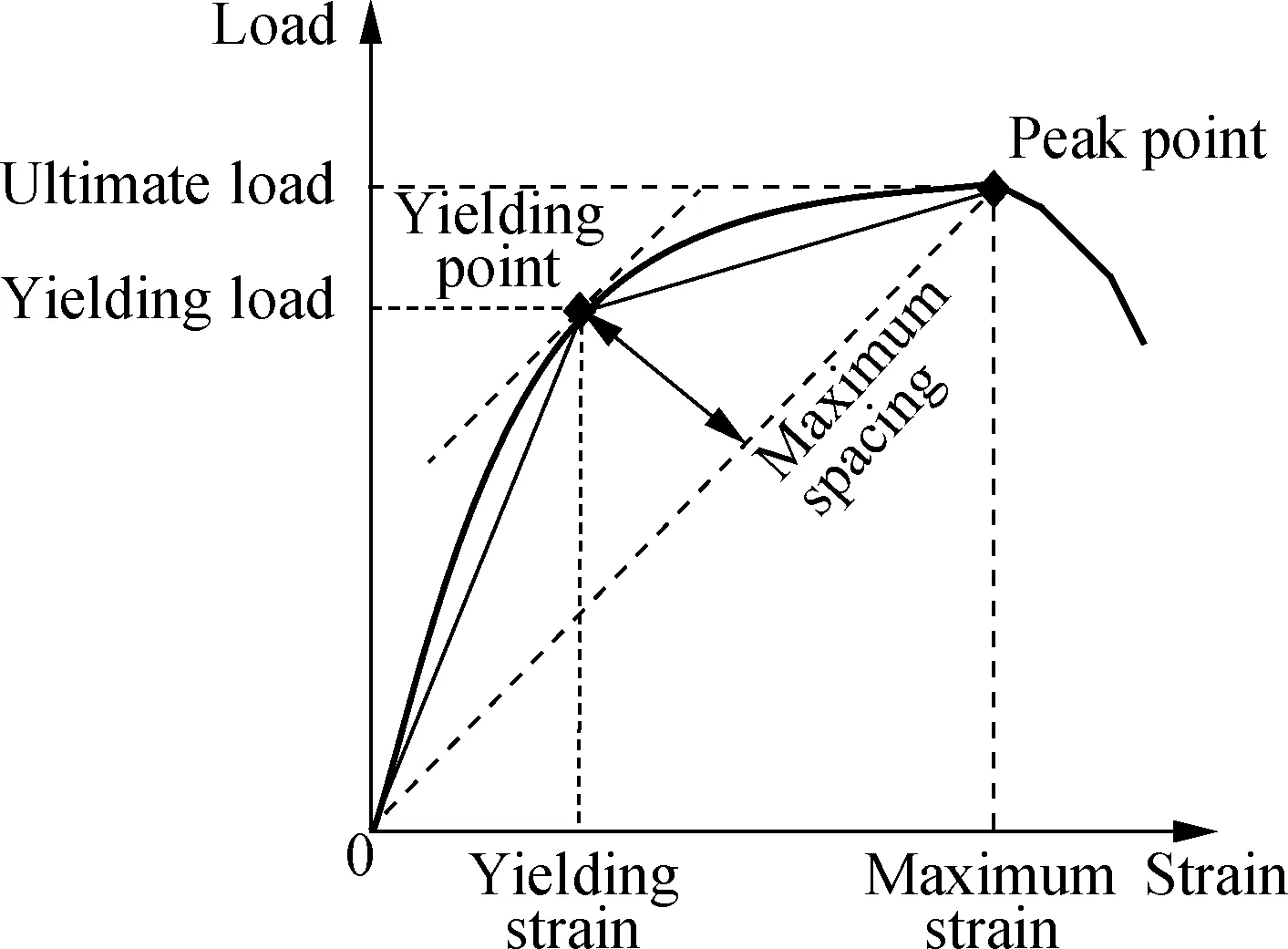
Fig.5 Proposed method for determining the yielding point

2 Test Results and Discussion

2.1 Failure modes and crack pattern

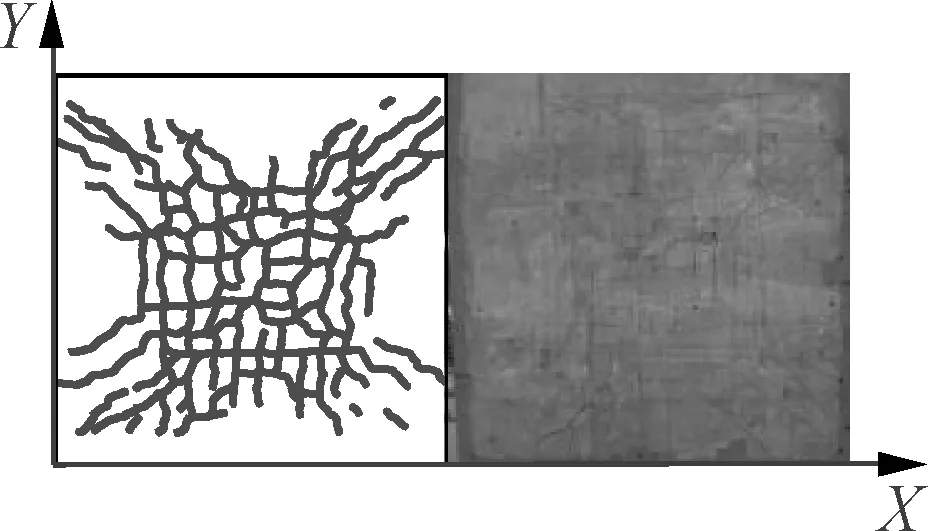
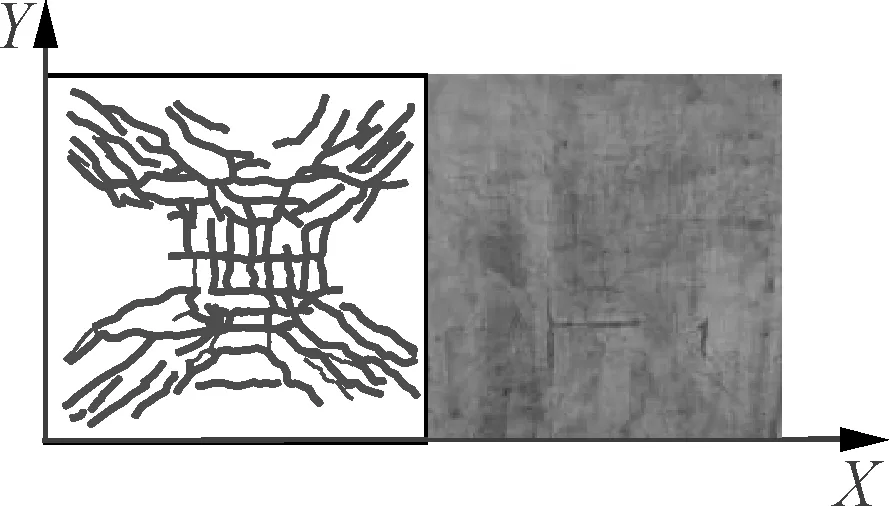
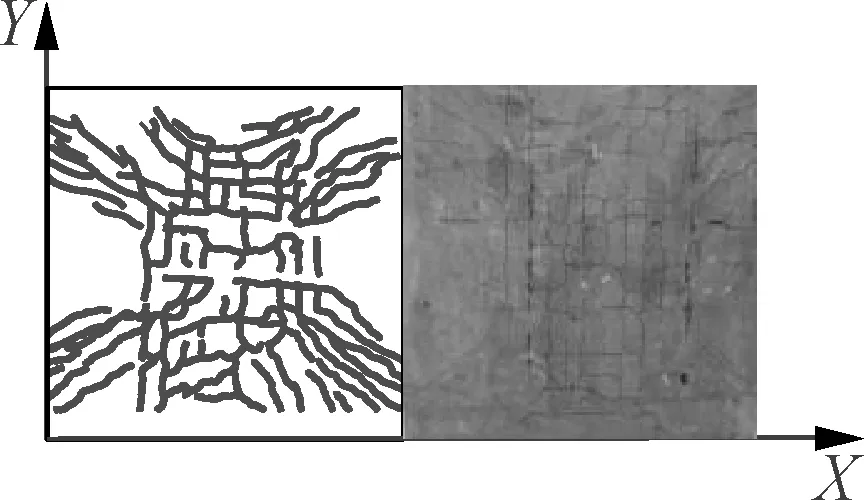
The following phenomena can be observed from the failure patterns of the five specimens as shown in Fig.6.

1) Throughout the experiment, the five specimens had similar responses to the external load, all of which went through the elastic deformation, concrete cracking, upward crack propagation, compressive bar yielding, continuous crack extension, and corner warpage. Ultimately, the specimens failed under deflection as the cracking exceeded the maximum limit, and exhibited a “butterfly” deformation pattern. There was neither shear failure inside the slab nor local punching failure at the pad. However, it is noteworthy that S2, S3 and S5 had much added distribution of cracks in theX-direction than in theY-direction at the mid-span of the slab, although the final cracks of all specimens were plastic yield lines exhibiting an “X” pattern. This is attributed to the shape difference of the precast base plate in the two directions and can be explained by the concept of the orthotropic reinforcement slab in Ref.[25].

2) Specimens with different base plate materials (S2 vs. S3) are compared. When the specimens reached the cracking load, it was observed that S2 had fewer cracks than S3, but its bottom and sides were much less cracked than those of S3 near the end of the elastic-plastic phase. A possible reason can be found in Ref.[26]. When specimens were subjected to a small load, the steel fibres in the matrix hindered the expansion of cracks in the concrete, enhancing the crack resistance of brittle matrix material under bi-directional tension. In the later phase of loading, however, steel fibres were broken and even pulled out, as the anchorage length in the base concrete became insufficient.

3) Specimens in different shapes (S3 vs. S4 vs. S5 are compared). Throughout the loading process, our specimens neither exhibited any adhesion failure at the interface between the bottom plate and the concrete top, nor separation between the two components on the slab side (as evidenced by the load-slip curves in Section 2.5). This means that all the CCS shapes in our experiment ensure a good coordination between the base plate and the concrete topping.

(a)

(b)

(c)

(d)

(e)

2.2 Carrying capacity

Fig.7 presents the cracking loadPcr, yielding loadPyand ultimate loadPumeasured in the experiment. The load value of 78.12 kN was calculated by Load Code for the Design of Building Structures (GB 50009—2012) ; i.e., the variable load value was 2.0 kN/m2, and a value of 4.9 kN/m2was the permanent load value after taking into account the architectural practice.

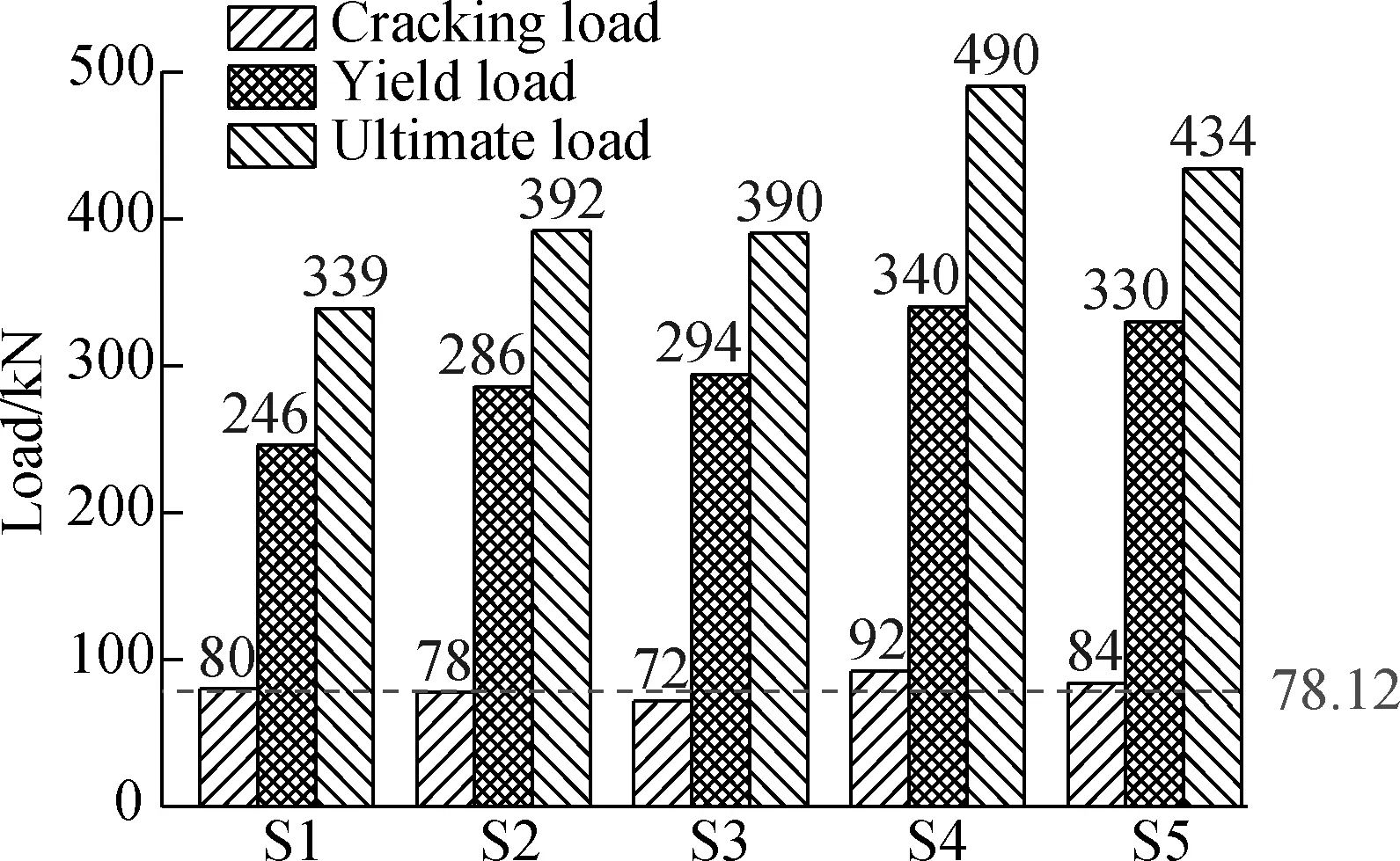
Fig.7 Characteristic load values of the specimens

1) S1 vs. S2 to S5. The five specimens displayed high load bearing capacities, which satisfied the load bearing requirements for residential buildings in the Chinese standard GB 50009—2012[27]. The ultimate loads of S2, S3, S4 and S5 were, respectively, 15.63%, 15.04%, 44.54% and 28.02% higher than the ultimate load of S1. This is because the load bearing capacity of the cast-in-situ concrete slab can be easily outweighed if the CCS has a rational shape, despite the connecting interface between the precast base plate and the concrete topping.

2) S2 vs. S3. The two specimens shared similar cracking loads, yielding loads and ultimate loads, indicating that the SFRRAC base plate can satisfy the load bearing requirements for the CCS in the Chinese standard JGJ 1—2014[21].

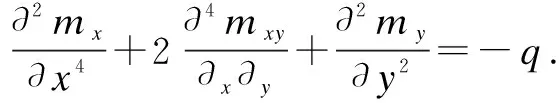
2.3 Deflection and ductility

2.3.1 Load-deflection curves

The mid-span load-deflection (F-δ) curves of our specimens are presented in Fig.8. The ductility index, i.e. the ratio of the ultimate deflection to the deflection at the yielding of compressive bars[29], is shown in Tab.4.

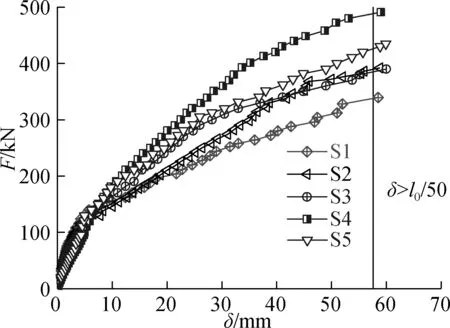
Fig.8 Load-deflection curves at mid-span

Tab.4 Ductility of the specimens

1) S1 vs. S2 to S5. Similar trends can be observed from the load-deflection curves of the five specimens in the experiment. The curves were approximately straight lines at the beginning of loading and became nonlinear after the concrete cracked. Moreover, the line segment of each curve between the elastic-plastic phase and the failure phase was very long and the ductility index had a high value, which signify the good ductility and bending performance of all specimens. Unlike the uni-directional CCSs in Refs.[30-32], the curves of our specimens always maintained a growing trend until the end of loading, due to the tensile membrane effect in the later phase of the bi-directional reinforcement.

2) S2 vs. S3. As steel fibers can inhibit concrete cracking, the slope of curve S3 was larger at the early stage of the elastic phase and the elastic-plastic phase than that of S2. Meanwhile, the slope of the S3 curve decreased faster than that of the S2 curve, as the steel fibres were pulled out from the bidirectional tensile zone at the bottom under the continuously growing load in the elastic-plastic phase. This is consistent with the experimental phenomenon mentioned in Section 2.1.

3) S3 vs. S4 vs. S5. In the later phase of loading, S4 had the lowest deflection under the same load. The ductility index of S4 was 7.60% and 14.05%, respectively, higher than those of S3 and S5. Therefore, the CCS were enhanced with steel bar truss in both theX- andY-directions can boost the load bearing capacity and enhance subsequent stiffness and ductility.

2.3.2 Flexural performance of two-way

The deflectionsδof each specimen at different positions in theX(W6, W7, W3, W8, W9)- andY(W1, W2, W3, W4, W5)-directions were recorded by the LVDTs in Fig.4(a) and plotted into curves in Fig.9.

1) S1 vs. S2 to S5. Under the same load level, the vertical displacement was negatively correlated with the distance between the measuring point and the slab centre. The curves all changed into a parabolic shape under

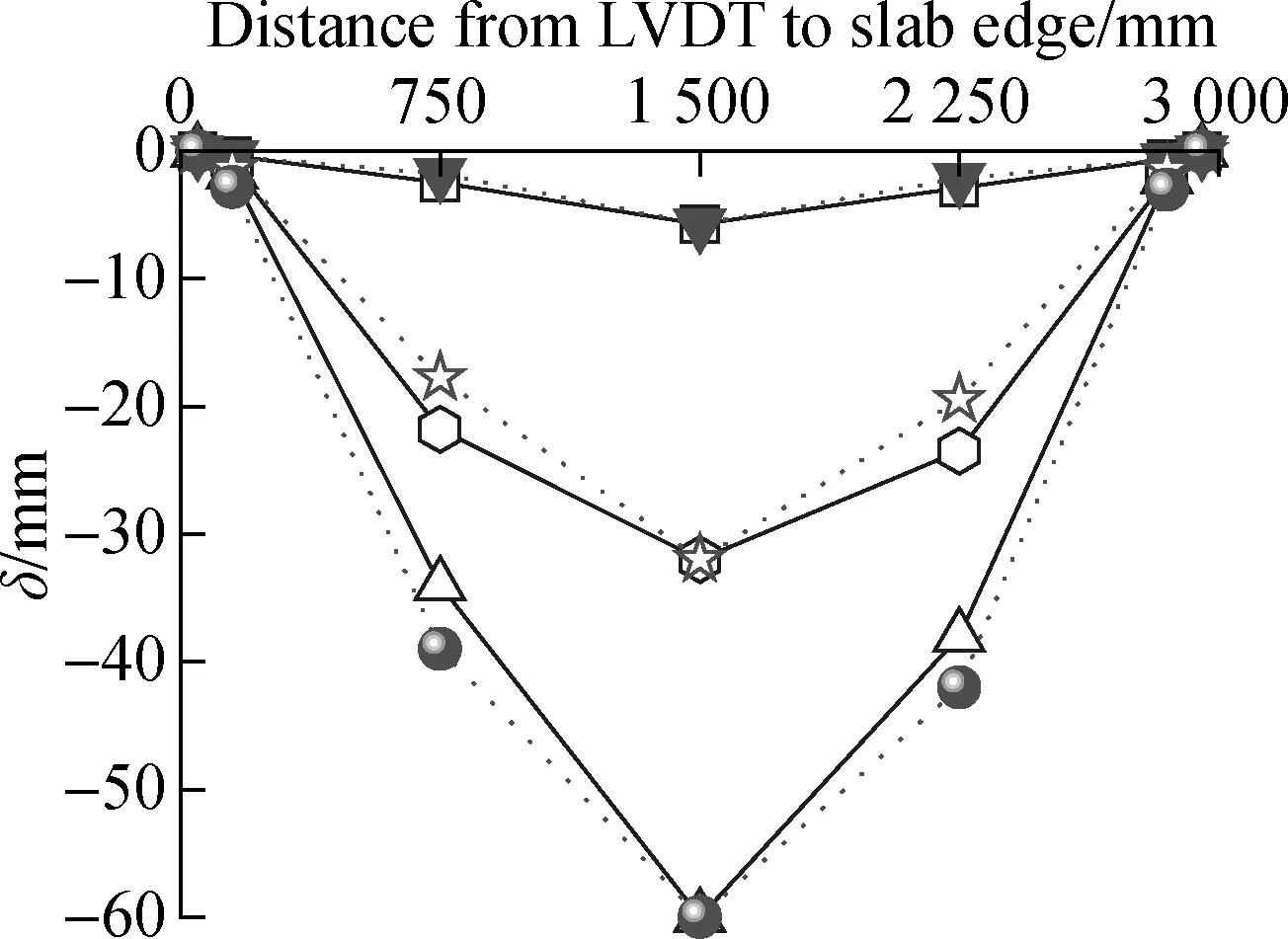
(a) (b) (c)

(d) (e)

Fig.9 Comparison of load-deflection curves at mid-span. (a) S1; (b) S2; (c) S3; (d) S4;(e)S5

each characteristic load, revealing the similarity in bending deformation between the four CCSs and the cast-in-situ concrete slab. Furthermore, the bending stiffness of the specimens decreased under the continuous cracking at the bottom centre, producing obvious inflection points in the curves under yield load and ultimate load.

2) S2 vs. S3. The vertical displacements of the two specimens were similar at cracking load, but different under the yielding load value and ultimate load value. The load-deflection curves of the two specimens were basically the same in theX- orY-direction throughout the loading process. As a result, the base plate material only affects the deflection of the CCSs under a vertical load, but does not affect the stiffness distribution of the slabs in either direction.

3) S3 vs. S4 vs. S5. The load-deflection curves of S3 and S5 started to differ in theX- orY- direction after cracking, which signifies the gradual change of bi-directional stress state of the two specimens, and the difference increased with the load. These phenomena can be explained by the property of the orthogonal anisotropic reinforcement slab in Ref.[25]. This property also explains the wider distribution of cracks in theX-direction than theY-direction at the mid-span of the slab when the specimens were ultimately destroyed in Section 2.1.

2.4 Bar strain

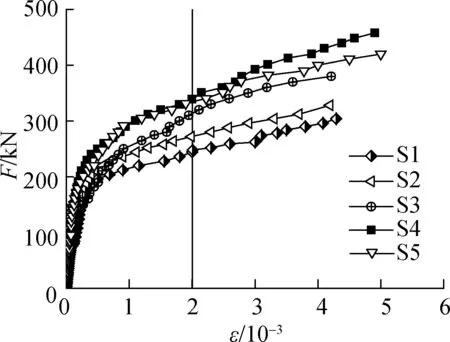
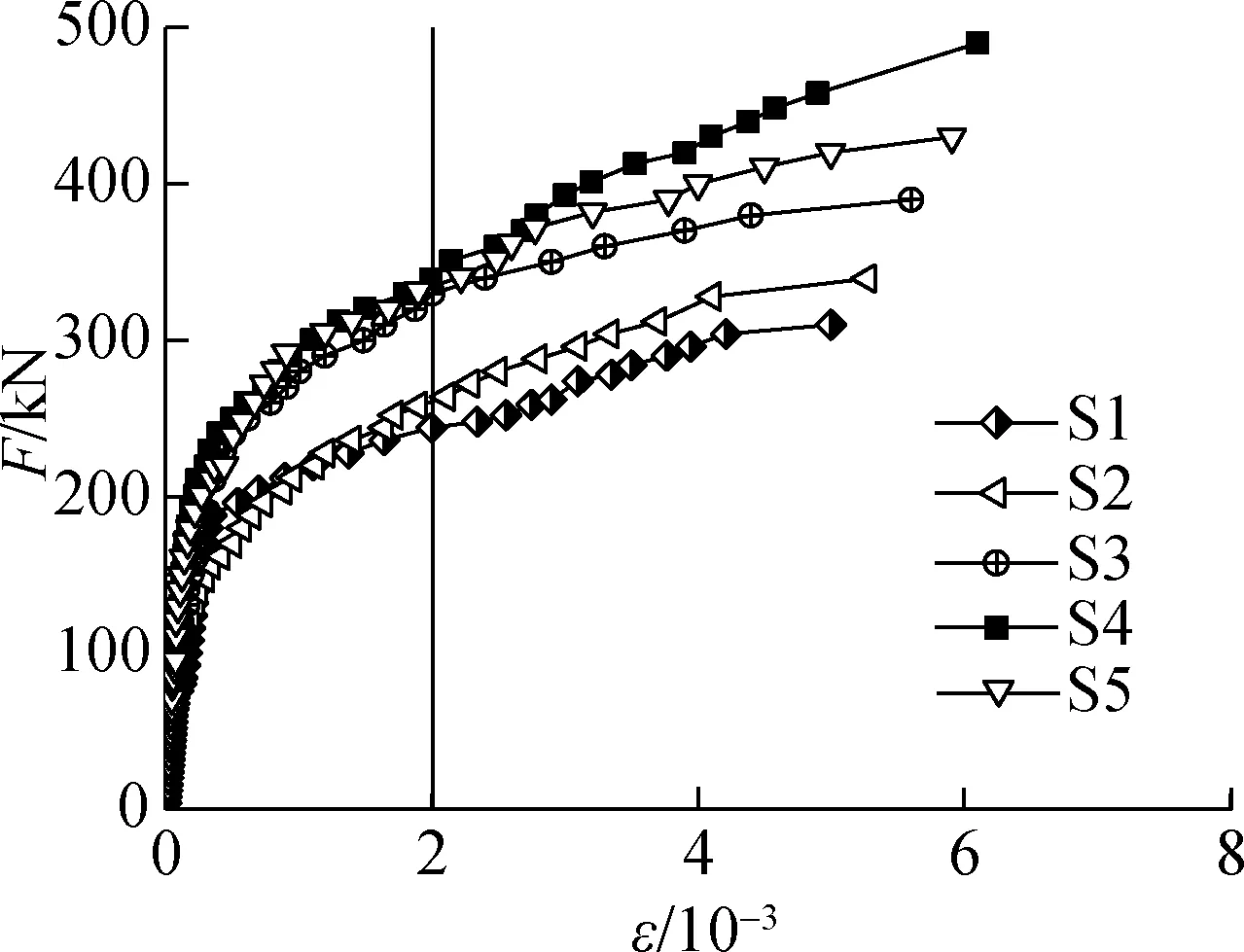
The mid-span load-strain (F-ε) curves of compressive bars at measuringX5andY5in Fig.4(b) are displayed in Fig.10.

(a)

(b)

1) S1 vs. S2 to S5. For all specimens, each load-bar strain curve consists of three segments: the straight segment before concrete cracking, the curved segment from cracking to bar yielding, and the smooth segment from bar yielding to the ultimate state.

2) S2 vs. S3. The load-bar strain curves of both specimens coincided with each other and increased proportionally before the concrete cracked. As the cracking continued to intensify, the strain of S3 fell below that of S2 under the same load level. The probable reason lies in that the load on the tensile zone of S2 was completely carried by the tensile bars after concrete cracking; by contrast, the steel fibres of S3 carried part of the tensile stress on the cracks and strengthened the bottom bars’ tensile strength.

3) S3 vs. S4 vs. S5. Under the same load level, the strain of S4 inX/Y-direction is much smaller than that of S3 or S5, because the load on the compressive bars in S4 was partially carried by the steel bar truss.

S4 was cited as an example to further illustrate the load-strain (F-ε) features of steel bar truss. The load-bar strain curve of this specimen was drawn according to the data recorded by the strain gauges of top/bottom chords and web members of truss reinforcement, which were arranged inXandYdirections, respectively. As shown in Fig.11, the bottom chords in both directions were subjected to tensile stress, and the strain reached the yield strain of bars when the specimen entered the failure phase. The web members and the top chords of the steel bar truss were also involved in load bearing. With the increase in load, the neutral surface of the specimen moved upward continuously. The stresses of theX-direction upper chord, web rod andY-direction web rod all shifted from compressive stress to tensile stress. It can be seen that the steel bar truss participated in the load bearing process, creating a reinforcement belt in the slab similar to that described in Ref.[33], which enhances the bearing capacity of the specimen.

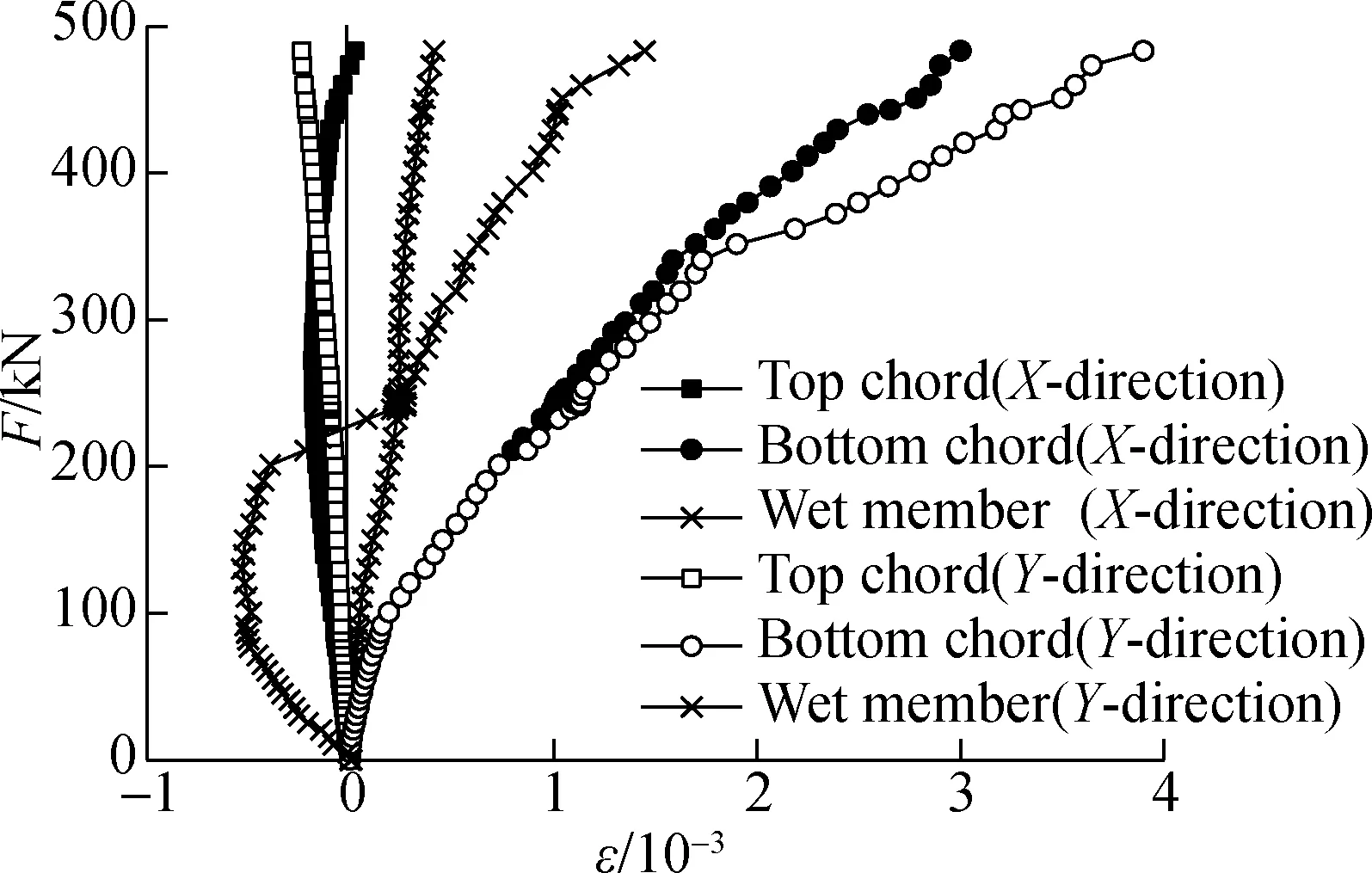
Fig.11 Load-strain relationship at the mid-span of longitudinal load-bearing reinforcements

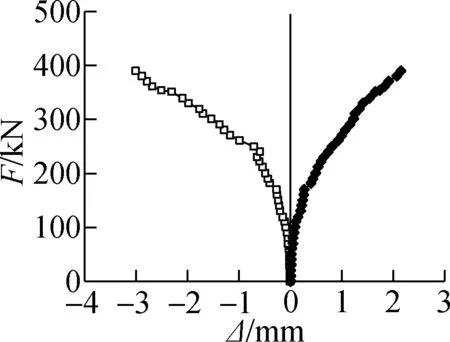
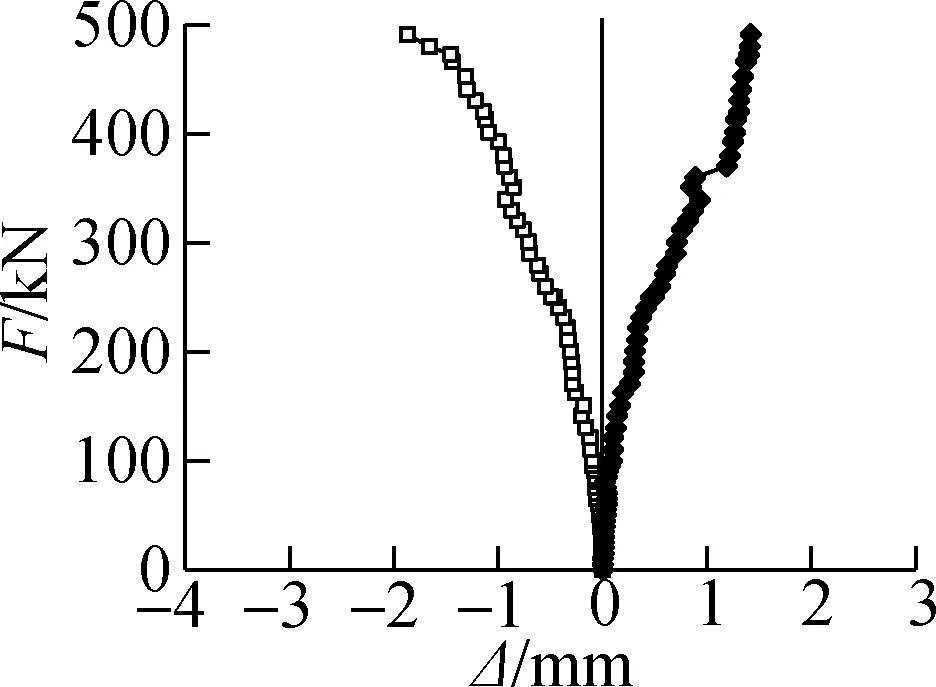
2.5 Load-slip curves

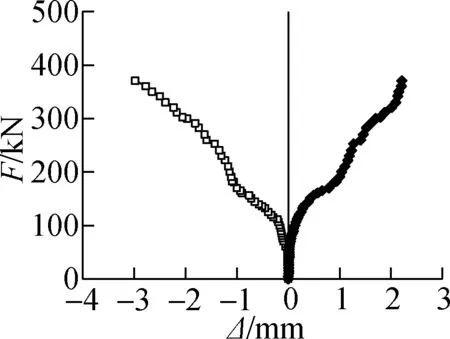
The load-slip (F-Δ) curves were plotted according to the two LVDTs placed at both ends of the specimens (i.e. W10 and W11). As shown in Fig.12, the load-slip curves reflect the good performance of the specimens under top compression and bottom tension. Considering that the connecting interface had no horizontal crack in the loading process (see Fig.3(a)), it is safe to say that our specimens performed well under the two forces throughout the loading process.

(a)

(b)

(c)

(d)

3 Flexural Capacity Analysis

3.1 Failure modes and crack pattern

As the failure mode of the CSSs is similar to that of cast-in-situ concrete slab, the bearing capacities of the four CSSs were computed using the plastic yield lines of rigid-plastic theory[34]. Whereas the base plate material and shape were proved to be the influencing factors of the ultimate bearing capacity and failure mode, the following assumptions were put forward for the calculation of ultimate bearing capacity.

1) Influence of base plate material. The contribution of steel fibres to bending bearing capacity was considered for S3 to S5, following the method in the Chinese technical specification CECS38: 2004[35]. In other words, the tensile zone at specimen bottom was treated as an equivalent rectangular stress zone.

2) Influence of steel bar truss. The analysis in Section 2.4 shows that the top chords and web members can bear fewer loads than the bottom chords. For simplicity, the load bearing capacity of the bottom chords was considered while ignoring that of the top chords or web members. The bottom chords were counted into the calculation area of the tensile bars.

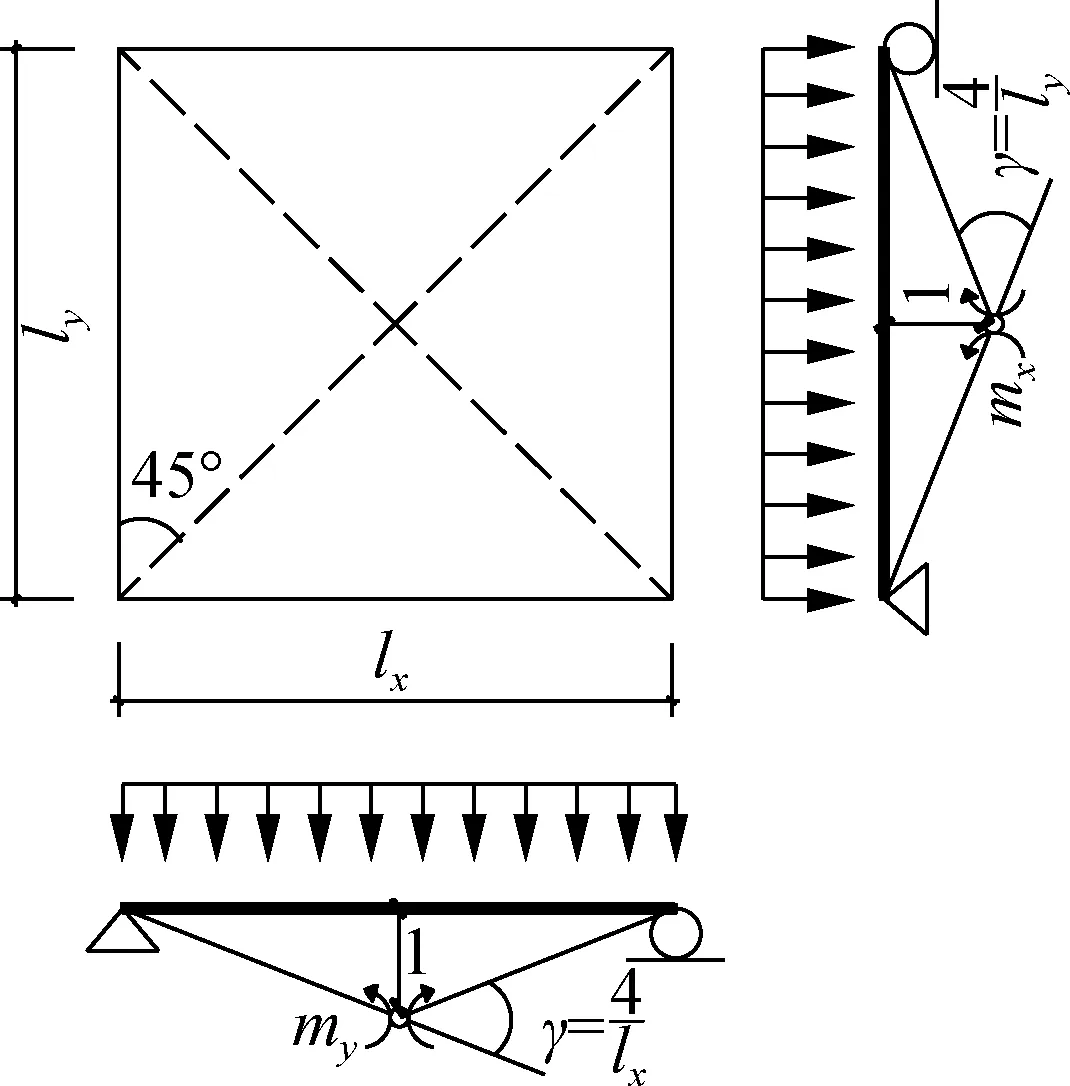
3) Influence of the base plate shape. The ultimate bearing capacity of S4 (see Fig.13(a)) was calculated according to the classical plastic yield lines of the bi-directional slabs simply-supported on four sides. Considering the difference between base plates of different shapes in theX- andY-directions, the ultimate bearing capacities of S2, S3 and S5 were computed according to the failure mode of the orthotropic reinforcement slab (see Fig.13(b)).

(a)

(b)

3.2 Calculation method for S2, S3 and S5

The failure mode in Fig.13(b) shows that the plastic yield line position of the three specimens under uniform load can be determined by the values ofθ(angle between the plastic hinge line andX-direction) ors(see Fig.13(b)). Letmxandmybe the ultimate bending moments per metre of the slab in theX- andY-directions, respectively. Then, the relationship between the mid-span ultimate bending moment in theX-direction and that in theY-direction can be expressed asmx=αmy.

Based on the theory of virtual work, when the failure occurs under the uniform ultimate loadqu, the mid-span virtual displacement of the specimen is one, and the virtual displacements at any other points areω(x,y), and the work done by the external force equals that by the internal force.

The external work done by the ultimate uniform loadqucan be expressed as

(2)

The work done by the internal force on each plastic yield line can be expressed as

(3)

AsWe=Wi, we have

(4)

wheren=lx/ly;α=my/mxis the ratio of the ultimate internal moment per unit length of the plastic hinge line perpendicular to the two principal axes of the specimen.

(5)

Then,θ=arctan(2s) can be drawn from the failure mode in Fig.13(b). It can be seen from Eq.(5) thatsorθcan be obtained from the failure mode when the value ofαis known. Depending on the materials, the calculation of ultimate bending moments of S2, S3 and S5 is divided into two cases.

(a)

(b)

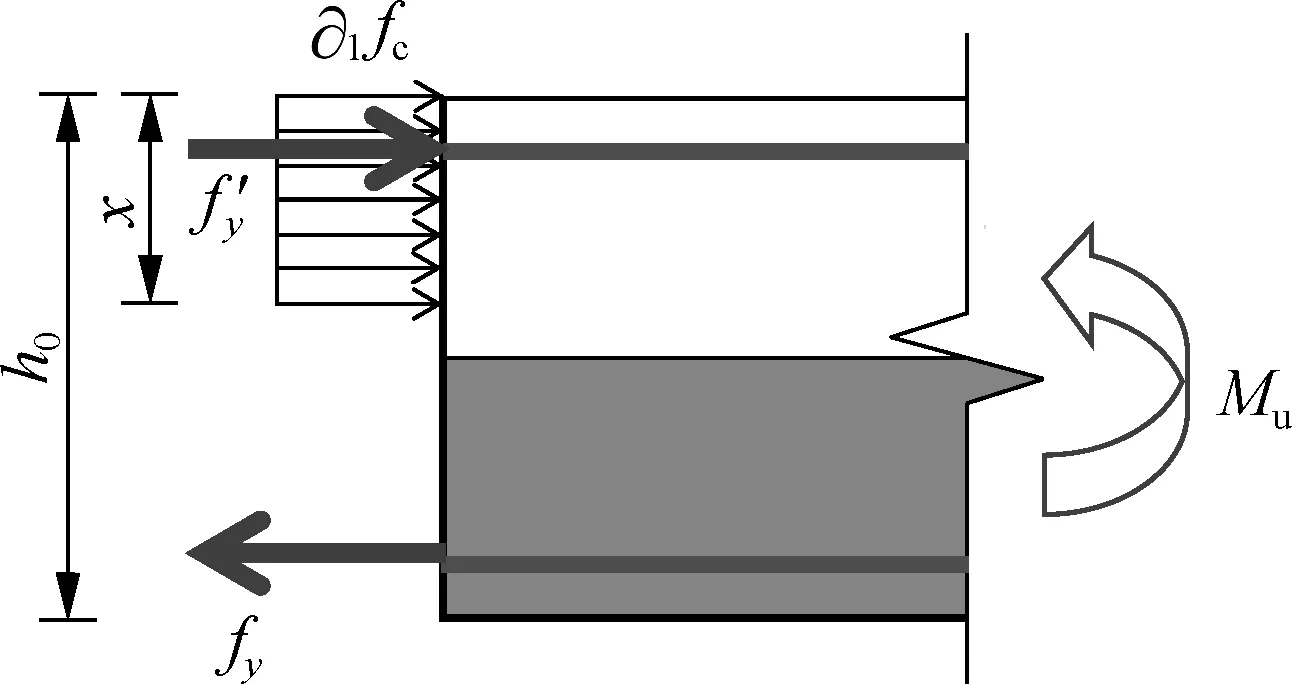
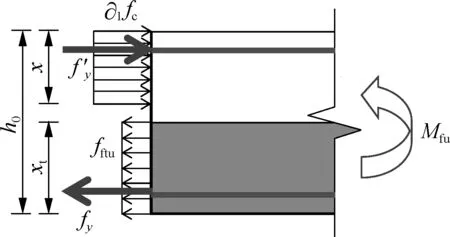
Case1For S3 and S5, the calculation method is illustrated in Fig.14(b).mxandmyare calculated by

(6)

whereAsxis the area of bar per unit width in theX-direction;Asyis the area of bar per unit width in theY-direction;fyis the longitudinal load-bearing bars tensile strength (the test value);h0xandh0yare the effective heights of cross-section;bx,by=1 000 mm;xxandxyare the heights of the concrete compression zone in theX/Y-direction, respectively;xxandxyare the heights of the equivalent rectangular stress in the tensile zone;fftuis the tensile strength of the equivalent rectangle stress pattern of SFRRAC in the tension zone at the ultimate capacity state, and this value is calculated by formulafftu=f1βtuλf.

Case2For S4, the calculation method is illustrated in Fig.14(b).mxandmyare calculated by

(7)

whereAstxandAstyare the areas of steel bar truss with bottom chord (X- orY-direction) in unit slab width.

Case3For S2, the calculation method is illustrated in Fig.14(a).mxandmyare calculated by[25]

(8)

Through the above methods, theθvalues of S2, S3 and S5 were calculated as 40.16°, 42.23° and 42.23°, respectively. Then, the ultimate bearing capacityquof each specimen can be obtained by Eq.(4).

3.3 Comparative analysis

Tab.5 lists the calculated ultimate uniform loadqu,cand the measured ultimate uniform loadqu,t. It can be seen that the calculated ultimate bending moments of the four CCSs specimens were basically consistent with the measured results. Except for S3, the relative errors of other specimens were controlled within 10%, indicating that the previous assumptions are valid. The authors believe that the reason for the large error of S3 may be the uneven mixing of steel fibers during the production of the prefabricated bottom plate. The results need to be further studied.

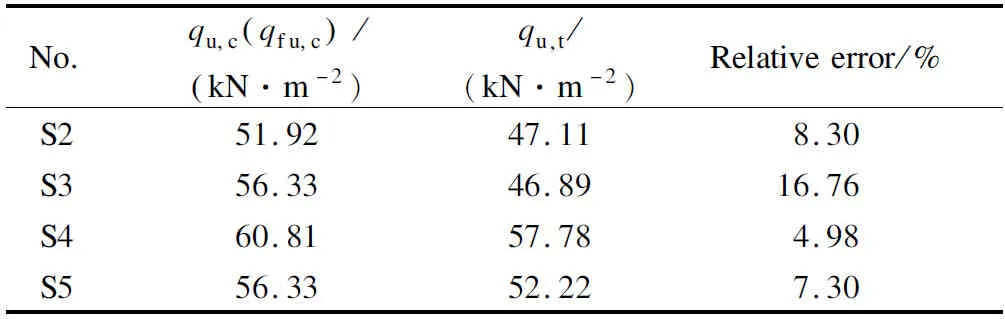
Table.5 Calculated and measured ultimate uniform loads

4 Conclusions

1) From loading to failure, the specimens with the SFRRAC base plate all went through the pre-cracking, cracking and failure phases. No horizontal slippage or destruction was observed on the connecting interface. The failure process of these specimens is similar to the specimen with the concrete base plate and that with a base plate recommended by the Chinese national standard. When the precast base plates are of similar structures, the SFRRAC CCS has a similar cracking load as the ordinary CCS, and a greater ultimate load than the latter.

2) The shape of the base plate has a major impact on the bearing capacity of the CCS. When a CCS is subjected to load in two directions, the bearing capacity can be effectively enhanced by adding reinforced interfaces, especially steel bar truss, in theX- andY-directions. According to the experimental results, the reinforcement modes can be ranked as follows by the contribution to the enhancement of bearing capacity: steel bar truss in both directions, steel bar truss in theY-direction and rectangular rib in theX-direction, and steel bar truss in a single direction.

3) The ultimate bearing capacity of the CCS should be calculated considering the effect of the base plate shape. In particular, the impact of plate shape on plastic yield line position should be taken into account during the calculation of the ultimate bearing capacity by the plastic yield line theory when the base plate has different shapes in theX- andY-directions.