借助地心引力突破画高难点
2021-01-11吴增寿
吴增寿
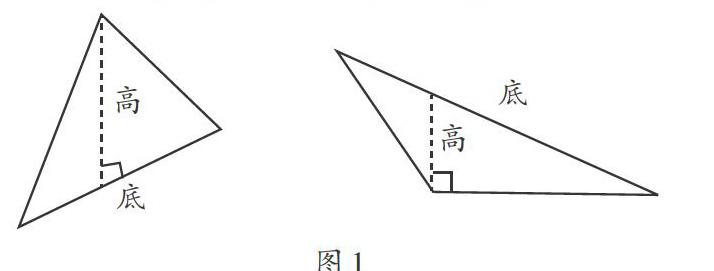

[摘 要]在学习画高的过程中,由于受生活经验的影响,很多学生画的高都是竖直的,即垂直于自己假想中的地面。受地心引力的启发,找到画高与生活的衔接点,即借助“地心引力下”的高类比三角形的高,实现了生活经验和数学知识的统一,破除了学生的思维定式,实现了知识的正迁移,解决了学生画高的难题。
[关键词]画高;地心引力;负迁移
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)02-0015-02
学生在画高的过程中经常会出现这样的错误:
从学生的错误当中就可以看出,不管三角形的底是否处于水平位置,学生所画的高永远是垂直于他们假想的地面。可见,生活经验影响了学生对数学中的高的理解。那么有没有更好的办法让学生理解数学中的高呢?难道生活中的高都是所谓的竖直方向的?难道就没有不同方向的高吗?我无意中看到了一张地球图(如图2),灵光一闪:谁说生活中就只有竖着的高,没有其他方向的高?在这张图上可以清楚看到,对我们来说,地球上的其他人和其他物的高不就是斜着的吗?这张图让我找到了生活与数学的衔接点。
于是,我有了下面的教学实践:解决生活中的高与数学中的高的矛盾,纠正学生头脑中高的方向都是竖直方向的片面认识,实现生活中的高到数学中的高的正迁移。
一、直观感知“地心引力”下的高,去除负迁移
学生作高的错误源于他们对高的片面经验,如果能在更大的视野下观察地球上的物体,就能去除这种片面经验带来的负迁移。
【教学片段1】
师:要想知道课桌的高,可以怎么测量?
生1:从桌面量到地面就可以了。
师:测量时应该注意什么?
生2:尺子要与地面垂直。
师:要想知道这位同学的身高,怎么测量?
生3:要从这位同学的头顶量到地面。
师:測量时要注意什么?
(出示PPT:观察桌子的高和这个同学的身高,这些高有什么相同的地方?)
生4:都是竖直方向的。
生5:都是垂直于地面的。
师:看来我们生活中的高都是测量从物体的最高点到垂直于地面的距离,这些高的方向都是竖直方向的。那么有没有高不是竖直方向的呢?
出示图3:
师:谁来指一指这些物体的高在哪里?(学生指,教师画)
师:这些物体的高的方向跟刚才高的方向一样吗?
生6:不一样。
师:那么有没有一样的地方?
生7:都是垂直于地面的。
师:是啊!尽管这些高的方向不一样,但都是垂直于地面的。
这个环节的教学不仅唤起了学生原有的生活中的高的经验,而且对接了学生在数学中的高的经验,尽管高的方向不同,但是高的本质是相同的,都是垂直于地面的,为学生接下来认识三角形的高做好经验上的铺垫。
二、借助“地心引力”下的高认识三角形的高,实现正迁移
为了更好地解决画高这个难点,必须解决什么是三角形的高的问题,从而更好地为后面的画高做好铺垫。
【教学片段2】
师:既然认识了生活中的高,那么今天这节课我们就来研究三角形的高。
出示图4:
师:这个三角形的高在哪里?
(学生指,教师画)
出示图5:
师:这个三角形的高在哪里呢?(学生思考)
师:请我们的地球来帮忙。假如这个三角形相当于一座山,那么它应该怎么摆在地球上呢?
(学生摆。如图6)
师:原来这座山是在地球的这个位置啊!那谁来指一指这个三角形的高在哪里?(学生指,教师画)
师:谁能用一句话来说一说什么是三角形的高?
生1:三角形的高就是三角形的一个顶点到三角形一条边的垂直线段。
师:这个点就叫作三角形的——
生2:顶点。
师:它的一条边是指哪一条边?任意一条都可以吗?
生3:和顶点相对的那条边。
师:这条边还有一个名字,叫作三角形的底。请和同桌说一说三角形的底和高。
出示图7:
师:如果这个三角形是这样立在地球上,底是哪一条?高又在哪里?
(学生指底和高)
师(边说边画):先找到三角板的两条直角边,用三角板的一条直角边与三角形的底重合,沿着底移动三角板,使三角板的一个顶点落在另一条直角边上,然后画垂线,标直角符号。
(学生模仿画,教师巡视指导)
出示图8:
师:如果这个三角形的底是这一条,高又该怎样画呢?先用手比画,然后再画一画。
(学生画,教师巡视指导)
师:同一个三角形,我们画了三条不同位置的高。为什么同一个三角形可以画出三条高呢?
生4:三角形有三条边,随便哪一条边都可以当作底。每条底上都可以画一条高,所以三角形就有三条高。
本环节分两步:第一步,先认识水平放置的三角形中的高和变式三角形的高,从而概括出三角形的高和底的含义;第二步,在认识高的基础上学习高的作法,同时在画高的过程中不断积累一些画高的经验。
其实这里关键的是第一步中在变式三角形中怎么找高,这也是学生画高的含糊点,然而这里借助“地球爷爷的手”——地心引力,让数学的高和生活中的高无缝对接,让学生明白原来只要把三角形想象成立在地球上的样子,那么高就垂直于地面的方向,实现了生活中的高和数学中的高的统一。
这样一来,借助“地心引力下”的高类比三角形的高,实现了生活经验和数学知识的统一,破除了学生的思维定式,实现了知识的正迁移,解决了学生画高的难题。
(责编 金 铃)
