解决多属性群决策问题的一种线性规划法

2021-01-11朱国成陈粟宋

顺德职业技术学院学报 2021年1期

朱国成，庄乐，陈粟宋*

（1.广东创新科技职业学院通识教育学院，广东东莞 523960；2.广东石油化工学院理学院，广东茂名 525000）

解决多属性群决策问题方法的核心思想是利用从现实世界获取的决策信息数据通过数学模型的处理达到区分决策方案优劣的目的。目前国内外学者在该领域的研究方向主要从决策获取的信息数据类别、决策信息数据的异同程度以及信息数据集结方法等三个维度出发。决策信息类别方面，文献［1］开创性的提出模糊决策以后，不同类别的决策方法相继被提出，如直觉模糊多属性决策［2］、语言多属性决策［3］、犹豫语言多属性决策［4］、区间值信息多属性决策［5］、Pythagorean 模糊多属性决策［6］、犹豫模糊多属性决策［7］、概率犹豫模糊多属性决策［8］等。以上众多类别决策方法优缺点并存：其对于不同信息特征有针对性的制定决策规则，能够取得科学决策结果，但是决策过程或结果仍然有讨论空间。例如，犹豫模糊多属性决策方法解决了评价专家评价认知犹豫问题，但决策过程中需要先对犹豫模糊元中的决策数据信息进行集结，而后再融合方案的信息数据，整个决策过程牵扯到多次数据信息的集结，每次集结都无法避免损伤决策信息；概率犹豫模糊多属性决策方法虽很好兼顾了专家支持强度问题，但目前急需破解决策结果概率信息随着元素数量的增加而快速衰减的难题。同时以上不同决策方法解决的都是特定决策信息情境下的问题，不同决策方法之间的相互转换很难实现，这大大限制了各种决策方法的使用范围。在解决多属性决策信息的异同程度方面，通常采用信息熵测度［9］、距离测度［10］、相似性测度［11］等。以上三种不同类型信息测度不仅能够描述决策因素蕴含信息量分布情况，而且还能刻画不同决策方案之间及决策方案内部各因素之间信息量差异特征。例如，TOPSIS 利用贴近度指标解决了一类多属性决策问题；ELECTRE 决策利用距离测度作为工具构造一类多属性决策方法等，因为三类不同测度在多属性决策过程中的应用具有一定共性，故三者之间在一定条件下可以相互转化。信息测度由于利用数学模型计算，拥有很强的数学理论依据，容易“让人信服”，但计算过程相对复杂，同时考虑到整个决策过程只从数据出发，容易忽略人的感情因素及周围环境的动态变化，造成决策结果与人的主观意愿可能有较大出入。在决策信息数据集结方法上主要通过构造集结算子实现的，国内外学者从不同角度定义了非常多的集结算子，比较具有代表性的集结算子有有序加权集结算子［12］、直觉模糊加权集结算子［13］、诱导的犹豫模糊集成算子［14］等等。每一种算子都有其适用范围，未来怎样构建广义集成算子参数适用区间及新算子相关参数科学取值、相关联导出函数定义、算子的赋权方法等都有待于进一步探索和实践。

对于经典多属性决策问题，文献［15］、［16］采用模糊化属性数据的模糊干预方法决策，结果表明该方法科学有效。为了尽可能保留决策信息，文献［17］将属性确定数值映射为区间数，通过构造区间数排序准则对各方案比对决策。本文通过把值属形态为实数的属性值构造成区间数形式，利用区间数熵值法计算属性权重；采用单目标线性规划模型求解方案最优综合属性值，避免了通过集结算子实现对方案信息集结并排序，从决策结果来看，得到了理想方案，达到了科学决策目的，同时也丰富了多属性群决策理论知识，通过在教师教学评价当中应用，得出该理论具有一定参考及实用价值。

1 确定属性权重

定义1［18］设多属性决策问题有m个目标G1，G2，…，Gm和n个决策方案A1，A2，…An，设方案A1（i=1，2，…，n）在目标Gj（j=1，2，…，m）下的属性值为区间数为确数，且。从而构成决策矩阵A=（aij）n×m，最常见的属性类型有效益型和成本型两种，设Ii（i=1，2）分别表示效益型和成本型属性的下标集。称为目标Gj下理想属性值，若满足：j∈I1时等式，：当j∈I2时，

定义2［19］设a=［a-，a+］，b=［b-，b+］为两区间数，称D（a，b）为区间数a，b的相离度，其中D（a，b）=。显然D（a，b）越大，则区间数a，b相离的程度越大，特别地，当D（a，b）=0时，有a=b，即区间数a，b相等。

一般条件下，在多属性群决策问题中，假如有H个属性Gi（i=1，…，H）和K个决策方案，每个方案用符号表示为Pj（j=1，2，…，K），评价专家组中有E位专家，每位评价专家用符号表示为Al（l=1，2，…，E），第l位评价专家Al给第j个方案Pj中第i个属性Gi分数记为qlji。评价专家权重事先给出，属性Gi权重需要计算，属性Gi值构成的分数区间为［mi，ni］。属性分数的专家评分表形式是［qlji］E×K×H。将评价专家给方案评分表转换为区间数矩阵，形式，区间端点指专家组给第j个方案Pj中属性Gi评分最低值，max{qlji}指专家组给方案Pj中属性Gi评分最高值。

2）利用定义1、2 及与理想属性值之间的相离度，将区间数决策矩阵转化为相离度矩阵D=［dji］K×H；

2 多属性群决策步骤建构

设多属性群决策问题中有H个属性、K个决策方案，E个评价专家，分别用符号表示为：Gi（i=1，…，H）、Pj（j=1，2，…，K）和Al（l=1，2，…，E）。第l位专家Al给第个j方案Pj中第i个属性Gi分数记为qlji。专家权重事先给出，属性Gi的权重需要计算，属性Gi构成的分数取值区间为［mi，ni］。专家评分表形式为［qlji］E×K×H。将专家评分表转换为区间形式矩阵，其中，分别指加权的各位专家给方案Pj中第i个属性Gi评分的最低值与最高值。定义方案Pj中的属性Gi平均分数。

第六步：根据maxZ（Pj）大小，对各方案比对决策；

第七步：结束。

3 案例分析

以教师教学评价为例进行详细说明，设有四位督导构成评价专家组，每位专家用符号Al（l=1，2，3，4）表示，五位教师构成方案集，用符号Pj（j=1，2，…，5）表示，四位专家对五位教师教学进行评价，评价专家权重=（0.28，0.22，0.24，0.26）T已知，评教因素用符号Gi表示，Gi=［mi，ni］（i=1，2，…，14），评教因素权重未知，督导专家组从14 个评教因素方面对教师进行打分评比如表1 所示。

表1 专家评分表

3.1 计算评教因素Gi（i=1，2，…，14）权重

由1）中矩阵可得各评教因素理想值：

2）利用定义1、2 及与理想评教因素值相离度，将区间数决策矩阵转化为相离度矩阵D=［dji］5×14。

3）采用文献［18］中的方法计算各评教因素权重：

3.2 构造约束条件

1）将表1 转换为加权专家评分表如表2。

表2 加权督导评分表

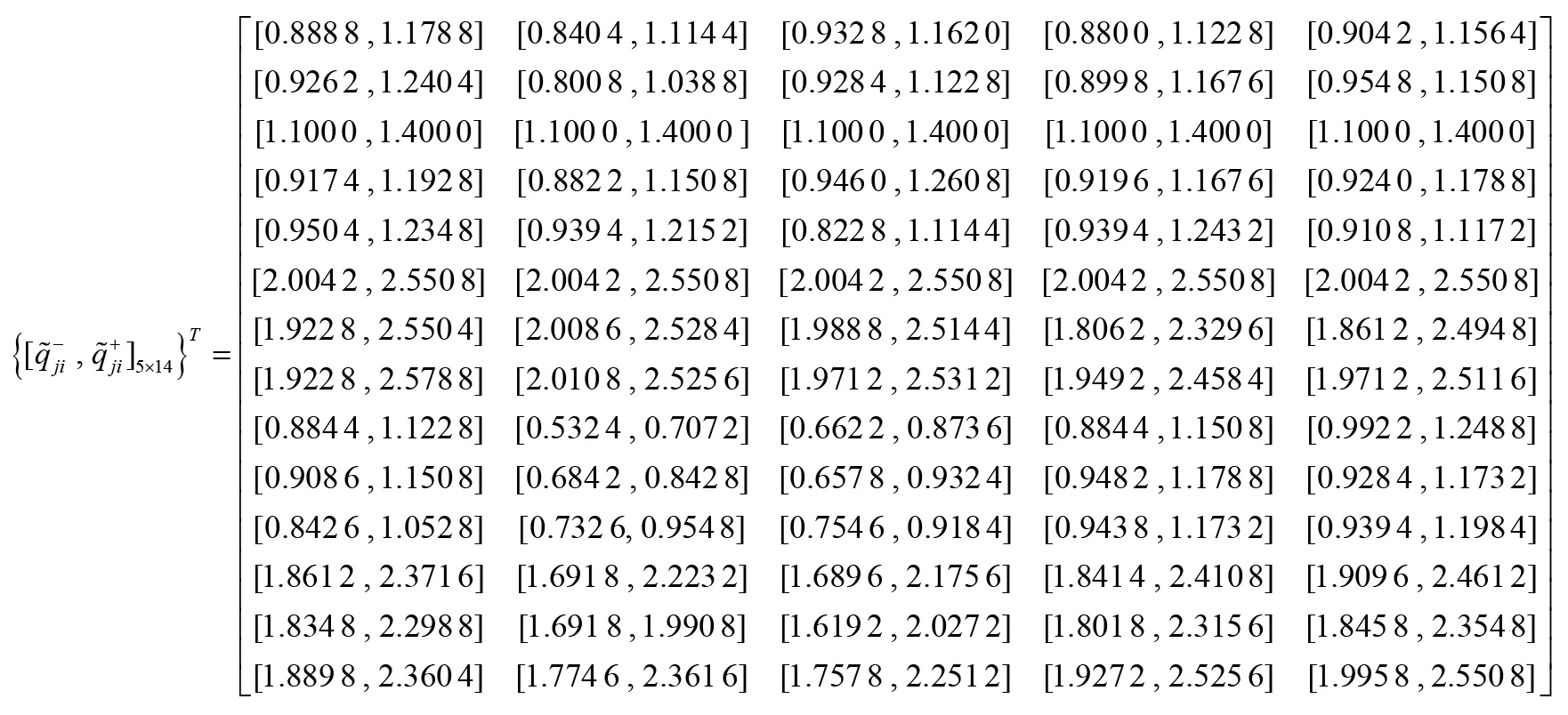
以教师P1为例：

4）构造每位教师综合评教因素值下的单目标线性规划模型。以教师P1为例：

以此类推，教师P2、P3、P4、P5综合评教因素值下的单目标线性规划模型分别如下：

5）利用MATLAB 计算得：

maxZ（P1）=1.514 9，maxZ（P2）=1.372 5，

maxZ（P3）=1.465 0，maxZ（P4）=1.514 9，

maxZ（P5）=1.515 0。

显然有：maxZ（P5）＞maxZ（P1）＞maxZ（P4）＞maxZ（P3）＞maxZ（P2）。

教师教学质量优良排序：P5＞P1＞P4＞P3＞P2。

与其它排序方法比较如表3 所示。

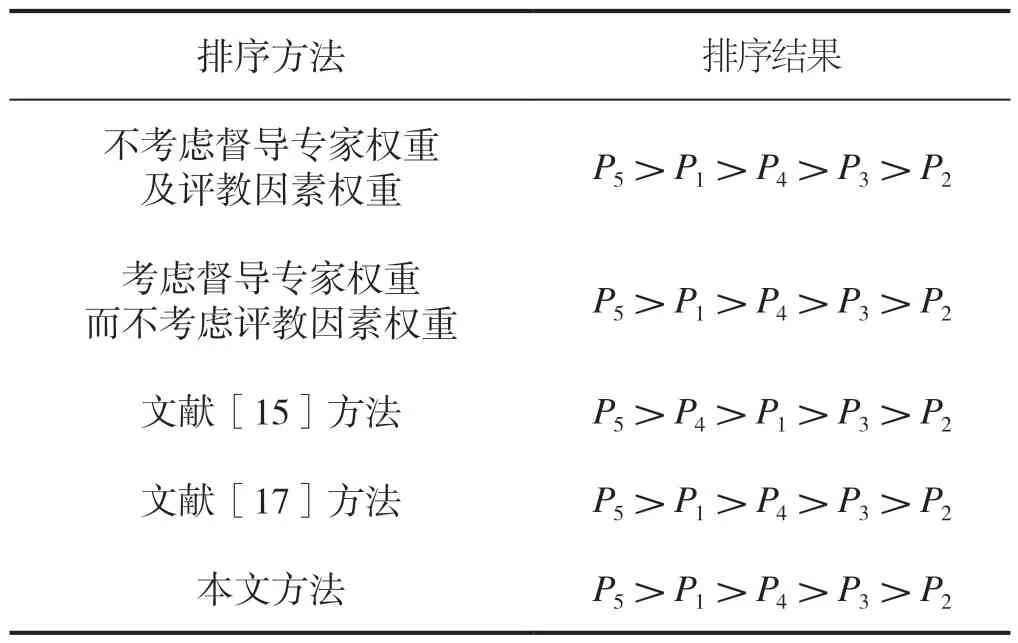
表3 排序方法比较

由表3 排序比较结果可知本文方法是有效的，从决策过程科学性角度来说，前2 种由于只单方面考虑权重，虽然结果一致，但方法有待商榷。文献［15］提供了一种解决传统多属性群决策问题的新方法——模糊干预法，保留了最优教师与最后一名教师的排序结果，只是对第一位教师与第四位教师的排序位置有争议。文献［17］排序手段虽与本文有较大差异，但结果完全一致。本文通过区间数熵值法计算属性权重，根据评教因素在决策中所起作用，有针对性重新分配权重。例如，督导专家给所有教师在第三与第六个评教因素上分数一样，这两个评教因素在决策过程中没有起到排序作用，所以无论其本身重要性程度如何，权重归零。