C8芳烃异构化催化剂内气相有效扩散系数的计算

2021-01-11肖昊阳唐晓津

石油炼制与化工 2021年1期

肖昊阳，唐晓津

(中国石化石油化工科学研究院，北京 100083)

C8芳烃是对二甲苯(PX)、间二甲苯(MX)、邻二甲苯(OX)和乙苯(EB)的总称[1]。PX是聚酯工业重要的化工原料，随着经济的发展，人们对PX的需求量日益增大，我国PX的需求量从2010年的0.93 Mt，迅速增至2017年的2.38 Mt，预计2022年将达到3.1 Mt左右[2-3]。近年来，随着国家政策的引导，国内芳烃联合装置不断增多，已有多家企业增设了PX项目，我国PX的自给率明显增加，PX产品供应因此发生巨大改变，市场竞争日益激烈，对该领域的技术水平及技术先进性有更高的要求，因此针对反应器开展设计和优化的研究工作，对芳烃产业有着重要的意义。

C8芳烃异构化是生产PX的重要技术路线，而反应器是实现异构化反应的核心设备，因此建立反应器数学模型对C8芳烃异构化反应器进行模拟和优化是非常必要的。在建立反应器数学模型时需要考虑到物料的质量传递，反应过程中传质的阻力主要集中于气相物质在催化剂内的扩散，而气相物质的有效扩散系数是表征其内扩散性能的重要参数，因此计算和确定C8芳烃异构化反应中气相组分的有效扩散系数对于完善C8芳烃异构化反应器的传质模型十分关键。

1 研究对象的选择

目前C8芳烃异构化反应器可分为径向、轴向和轴径向固定床反应器，由于径向固定床反应器具有流通截面积大、反应器压降小、产能大、费用低等优点[1]，故工业装置中大多使用该类型反应器，其示意见图1。气相原料从反应器顶部流入反应器内，然后沿器壁向下流动，原料气流动的同时沿着径向通过催化剂床层进行一系列化学反应，最后在反应器中心处汇合并流出反应器。

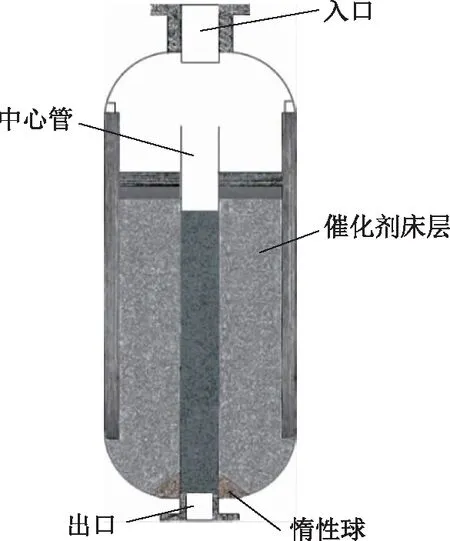
图1 C8芳烃异构化径向固定床反应器示意

根据EB转化方式的不同，C8芳烃异构化反应可分为乙苯转化型和乙苯脱乙基型两种路线，前者是将乙苯转化为3种二甲苯异构体，而后者是使乙苯转化为苯，乙苯转化型路线能将乙苯全部转化为二甲苯，乙苯的利用率更高，可使二甲苯的生产得以最大化[4]。以乙苯转化型工艺为例，反应路线简化为如图2所示的反应网络[5-8]，其气相组分包括OX、MX、PX、EB、甲苯(T)和三甲苯(TMB)。

C8芳烃异构化催化剂包含不同尺寸的孔道，气相反应物的内扩散过程是由大孔逐渐进入微孔。近年来对于C8芳烃异构化反应体系扩散系数的研究大多针对催化剂颗粒微孔内的扩散过程，并被用于研究反应的动力学。Elias等[9]得到了ZSM-5催化剂微孔内气相二甲苯异构体的扩散系数。李玉光等[10]在不同温度下分别得到了PX、MX在HZSM-5沸石微孔中的液相扩散系数和气相扩散系数。而宏观上C8芳烃异构化催化剂的孔径分布较为均匀，同时含有大孔和微孔[11]。气相物质在微孔内的扩散基本为Knudsen扩散，而在大孔中的扩散基本为分子扩散，并且大孔内的扩散过程对分子的运移起着主要作用[12-13]。

现有文献中对C8芳烃异构化催化剂内有效扩散系数的计算与试验数据较少，本课题建立催化剂内6种气相组分有效扩散系数的计算方法，并进一步讨论温度和压力对扩散系数的影响。

2 计算方法

C8芳烃异构化反应物料和大量循环氢混合并加热至反应温度后进入反应器内进行异构化反应。因此需要计算催化剂内如图2所示的各气相组分在氢气中的有效扩散系数。

气相组分在催化剂孔道内的扩散受到孔结构的影响，因此在近似处理催化剂孔结构模型时，要按照式(1)对气体分子扩散系数D进行修正，得到有效扩散系数De[14]：

(1)

式中：De为有效扩散系数，cm2s；D为气体分子扩散系数，cm2s；εp为催化剂孔隙率，无量纲；τ为催化剂的曲折因子，一般为1～6。

计算有效扩散系数的前提是确定气体分子扩散系数D。在催化剂的大孔中，分子的扩散阻力为分子间的碰撞，即主要特征为分子扩散过程。C8芳烃异构化反应压力一般为0.5～1.5 MPa，在此压力条件下，组成对分子扩散系数的影响较小，多组分气体混合物的扩散可用二元气体混合物的扩散系数计算式近似求解[15]。在C8芳烃异构化反应中循环氢气的体积流量占优，确定扩散系数时，可以采用式(2)所示的Chapman-Enskog关联式[14]计算进料中各种气相组分在氢气中的二元分子扩散系数DAB。

(2)

式中：DAB为二元分子扩散系数，cm2s；MA为A的相对分子质量；MB为B的相对分子质量；p为气相压力，bar(1 bar=0.1 MPa)；ΩAB为碰撞积分(无量纲)；σAB为Lennard-Jones势能函数的常数(特征长度)，Å(1 Å=0.1 nm)；ΩAB和σAB通过以下方法计算得到。

ΩAB是对比温度T*的函数[16]，可按Neufed方法[见式(3)]计算。

ΩAB=1.161 45(T*)0.148 74+
0.524 87exp(0.773 20T*)+
2.161 78exp(2.437 87T*)

(3)

T*=T(εABkB)

(4)

式中：εAB是Lennard-Jones能量，N·m；kB为波尔茨曼常数，1.380 649×10-23JK。

不同分子的σAB和εAB可由下式计算。

(5)

(6)

式中：σA、σB分别为纯物质A或B的Lennard-Jones长度，m；εA、εB分别为纯物质A或B的Lennard-Jones能量，N·m。εA、εB(统称为ε)和σA、σB(统称为σ)可近似由以下经验式计算[15]。

(7)

(8)

式中：T为气相温度，K；Tc为临界温度，K；Vb为纯物质A或B在正常沸点下的摩尔体积，cm3mol。

张克武等[17]根据分子力学理论和有机分子的半金属理论认为Vb遵循以下两条物理规律：①Vb随着相对分子质量的增大而增大；②微观粒子(包括分子整体，分子中的基团，定域键和电子等)的体积大小和分子结构(MS)相互依存，Vb由相对独立的ni个微观粒子的“元体积”Vi构成。并结合此两条规律总结出Vb的计算式为：

Vb=Mf(MS)=M[f(Wi)+f(We)]=
M(∑niWi+∑neWe)

(9)

式中：M为纯物质的相对分子质量；Wi为分子的基团效应参数；We为分子的电子效应参数；ni为组分i的基团数目；ne为e类电子效应数目。研究者[17]同时给出了不同基团(或定域键)的Wi与We，将数值代入式(9)中即可求得Vb。

根据上述方法得到Vb后，即可带入式(7)和式(5)分别求出常数σA，σB，σAB。根据式(8)得到εkB的值，将式(6)变形为式(10)，则便于进一步求解碰撞积分。

(10)

将所得到的各个参数代入式(2)，即可计算出分子扩散系数。而后，进一步通过确定催化剂颗粒的空隙率和曲折因子来得到有效扩散系数。

催化剂的曲折因子大多由试验得到，在工程上估算时，无表面扩散的情况下一般可取值为2～4[14]。王桂荣等[18]认为多孔催化剂的曲折因子不随扩散组分的种类和浓度的变化而改变。Sharma等[12]认为催化剂的曲折因子和催化剂颗粒的孔隙度有关，当孔隙率大于0.4时，曲折因子急剧下降，当孔隙率小于0.2时，曲折因子的值则很高。Sharma[12]研究了二甲苯异构化的SiO2Al2O3催化剂的微孔扩散，利用圆柱孔模型得到He、N2两种气体通过催化剂的曲折因子分别为2.4和2.0。

李清阳等[19]研究了18种铜基催化剂的孔隙率，发现随着孔隙率的增大，气体在催化剂颗粒内的扩散变得更加有利。有效扩散系数的值随着大孔孔隙率的增大而变大。根据文献研究[14，20]，本课题将C8芳烃异构化催化剂的孔隙率确定为0.4，曲折因子取值为2.0。

3 计算结果与讨论

3.1 方法的可靠性

利用上述方法，对温度为628 K、压力为0.18 MPa条件[11]下C8芳烃异构化催化剂内气相组分MX，OX，PX，EB，T，TMB在H2中的分子扩散系数(D)进行了计算，并求得有效扩散系数(De)，结果列入表1。

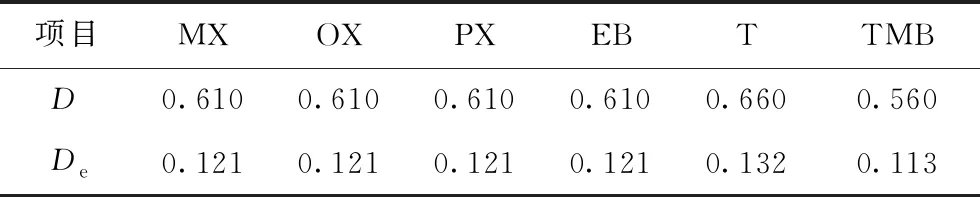
表1 C8芳烃异构化催化剂内气相分子扩散系数和有效扩散系数 cm2s

项目MXOXPXEBTTMBD0.6100.6100.6100.6100.6600.560De0.1210.1210.1210.1210.1320.113

张晓东等[11]釆用HZSM-5分子筛催化剂，在0.18 MPa压力条件下以H2为载气脉冲注入二甲苯的各异构体进行反应，根据不同粒度催化剂反应结果差异，得到相同温度和压力下二甲苯、甲苯和苯的产物分布，得出二甲苯组分的分子扩散系数D为0.52。

可见，本课题所计算出的D与文献[11]所得数据基本一致，说明采用本课题的方法估算出的扩散系数具有参考意义。

3.2 C8芳烃在H2中的分子扩散系数

利用所建立的计算方法，计算不同压力和不同温度条件下进料中6种物质MX，OX，PX，EB，T，TMB的气相组分在H2中的分子扩散系数，结果如图3～图8所示。

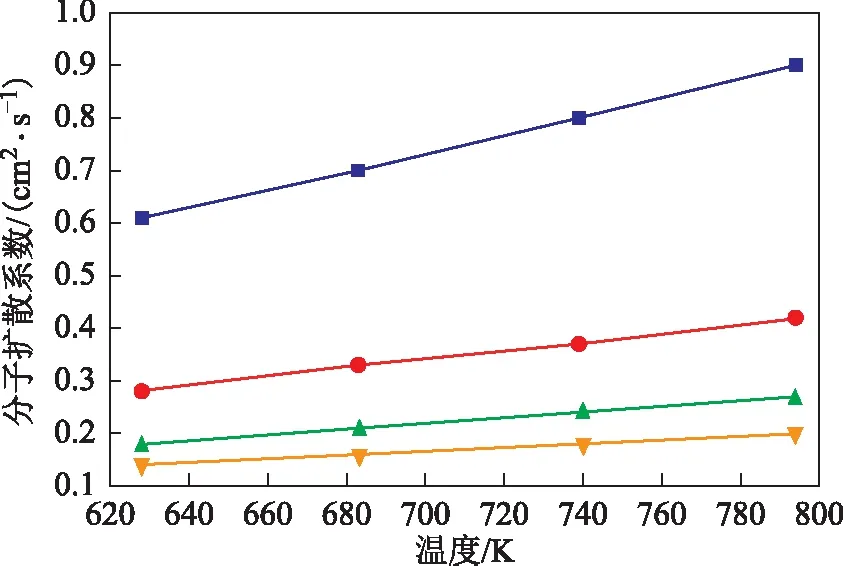
图3 MX气体在H2中的分子扩散系数压力,MPa:■—0.18； ●—0.39； ▲—0.60；图4～图8同

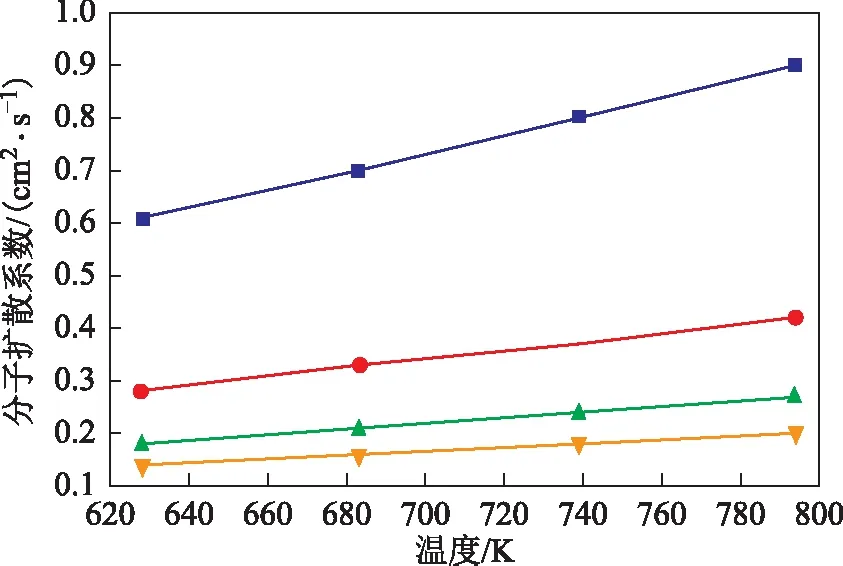
图4 OX气体在H2中的分子扩散系数

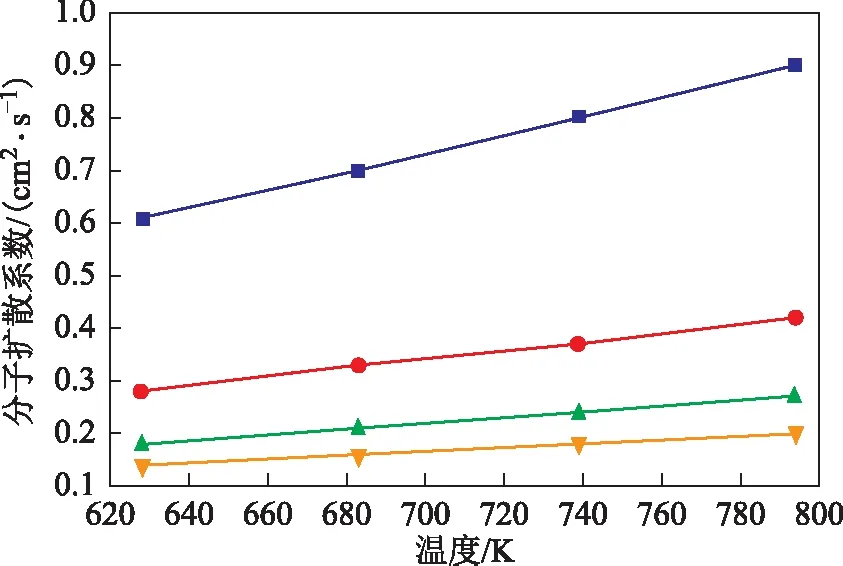
图5 PX气体在H2中的分子扩散系数

图6 T气体在H2中的分子扩散系数

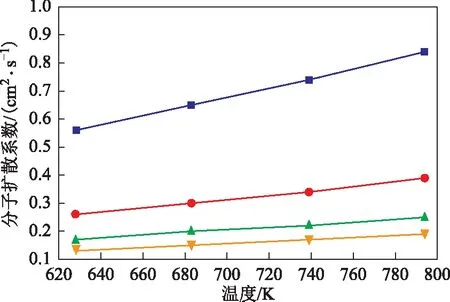
图7 TMB气体在H2中的分子扩散系数

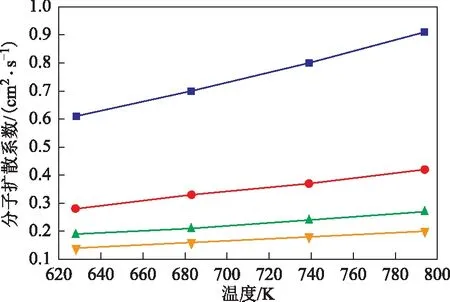
图8 EB气体在H2中的分子扩散系数

由图3～图8可知，在一定压力下，随着温度的升高，气相组分在H2中的分子扩散系数增大。分子运动论能很好地解释这一规律，气体分子的平均动能随着温度的升高而逐渐越大[21]。因此，在较高的温度下，气体分子的运动速率将加快，分子的扩散速率也会随之增大，分子扩散系数与温度成正比关系[22]。另外，当温度一定时，压力与分子扩散系数成反比关系。密度能够反映分子排布紧密程度，由理想气体状态方程可知，提高气体的压力，气体密度也会随之增加，这将导致分子间的距离减小，同时加大分子间的作用力，限制了分子的扩散，从而使得分子扩散系数减小[23]。