黏弹性支撑桩桩底行波反射特征研究

涂 园 ，王奎华 ，刘 鑫 ，Faheem Rizvi ，邱欣晨

(1. 浙江大学滨海和城市岩土工程研究中心，杭州 310058；2. 浙江省城市地下空间开发工程技术研究中心，杭州 310058)

桩底土的状态，或桩底的支撑条件对桩基静态承载性能[1]和桩基动力特性等[2]方面均有着显著影响．研究表明，桩底沉渣过厚，或桩端刚度过小，不仅会影响桩基极限端阻力的发挥，还可能影响桩侧摩阻力的分布[3-5]，在软土地区还会增加桩侧负摩阻力[6]，进而降低桩基竖向承载力，增加桩顶沉降．对于混凝土灌注桩，现行规范[7-8]对桩底沉渣厚度有着严格要求，尤其对于端承桩或嵌岩桩，桩端条件甚至直接决定了桩基极限承载力[9-10]，工程上也常常通过桩底注浆[11]的方式来改善桩底支撑条件．

然而目前在工程上，对桩端条件的检测和判断却仍较为模糊，缺乏定量判断方法和标准．工程上最常用的桩底检测方法有取芯法、低应变反射波探测法等[12]．前者虽然能够直接对桩底土进行采样，但该方法费时耗力成本高，尤其对于长桩而言，对孔的垂直度要求高．钻孔也破坏了桩体本身，工程上不宜大量使用；后者则是一种无损检测方法，根据桩顶速度响应来进行桩底检测和判断．但该法主要适用于基桩浅层缺陷检测、桩长和波速测量等方面．由于桩周土阻尼、桩身材料阻尼以及桩身缺陷等因素的影响，行波沿桩身传播不断衰减，桩底信号常常不明显(尤其对于长桩而言)，因此这一方法通常也只能对桩底支撑条件作定性判断[13]，例如，若桩顶入射速度与反射速度方向相同，则桩端更接近于自由端；若两者相反，则桩端更接近于固定端．现有的这两种检测方法均无法对桩底条件进行准确判断，工程上也往往存在许多桩底条件未知的基桩，因而存在一定的安全隐患，尤其对于那些采用嵌岩桩，或桩底土层条件要求较高的端承桩的工程．

另一方面，关于低应变条件下桩基纵向振动的研究成果虽然已经十分丰富，但研究主要集中在桩顶动力特性[14-15]和桩土相互作用模型上，对桩底界面反射特征的研究还较少涉及．即使涉及到桩底土时，也主要研究桩底条件对桩顶响应的影响，如王腾[16]采用黏弹性桩底模型研究了桩顶动刚度和动阻尼的影响，杨冬英[17]研究了不同桩底支撑模型对桩顶速度幅频曲线和时域曲线的影响，王奎华等[18-19]采用虚土桩模型研究桩底沉渣特性对桩顶动力响应的影响，李振亚等[20]采用行波分解法研究了桩底土剪切波速对被测截面的时域速度曲线的影响．目前对桩底反射特性的认识，仍停留桩底为自由端或固定端这样的特殊桩端条件下[21](见图1)，而对一般支撑条件下的桩底反射特征缺乏系统理论分析．

图1 桩底截面处入射速度和反射速度的关系Fig.1 Relationship between incident and reflection velocities at pile bottom

因此，本文主要研究了一般支撑条件下的桩底界面行波反射特征，基于此探讨了桩底条件的定量判断方法．桩底界面反射特征理论上仅与桩-桩底土界面性质有关，在桩身材料和尺寸已知的情况下，仅与桩底土的性质有关．研究桩底界面反射特性，可避免讨论桩周土阻尼、桩身材料阻尼和桩身缺陷等因素的影响，从而为定量判断桩底支撑条件提供可能．本文的理论推导基于一维行波理论，桩底土在低应变条件下(轻敲桩顶)的作用一般采用线性黏弹性模型来模拟，即把桩土相互作用简化为一个与位移成正比的线性弹簧和一个与速度成正比的线性阻尼器并联的Voigt体，该模型是最常用的一种桩底模型，也已在理论上和实践中均证明是适用的．在桩底截面通过傅里叶变换推导反映上、下行波关系的频响函数，并利用MATLAB 编程得到了下行波速度为半正弦脉冲，桩底为不同支撑条件下的上行波速度曲线，研究曲线特征与桩底土相对刚度系数和阻尼系数的关系；最后利用尼龙棒作为模型桩在室外开展试验，通过测量桩底在不同条件下的加速度、应变等物理量，对理论计算结果进行了验证．研究成果对一般支撑条件的桩底特性理论研究，以及桩底支撑条件的定量检测方面具有一定的理论价值和工程应用价值．

1 理论分析模型

1.1 桩底行波频响函数

由桩的一维波动方程可知，动力条件下桩身任意截面上的力波Pm可由下行力波dP 和上行力波uP 叠加形成，即

图2 中，用黏弹性支撑模型模拟桩底土的作用，则在桩底截面有

式中：Rs为桩底土反力的刚性力部分；Rd为桩底土反力的阻尼力部分，两者分别按式(3)和式(4)进行计算.

式中：k为桩底土的弹性系数；c为桩底土的阻尼系数；um为桩底截面位移；t为时间．

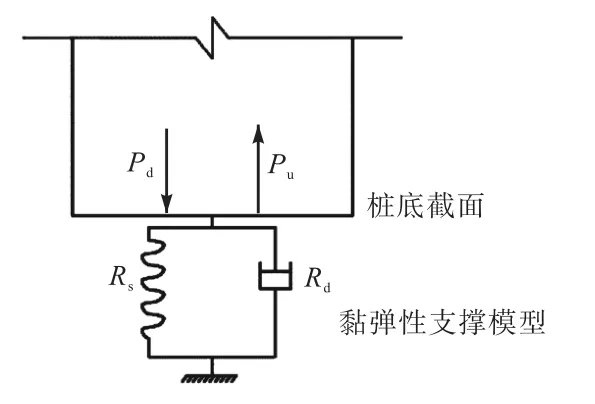
图2 桩底土黏弹性支撑模型Fig.2 Viscoelastic model of soil at pile tip

一维行波理论中，桩底截面处质点速度vm和位移um同样满足

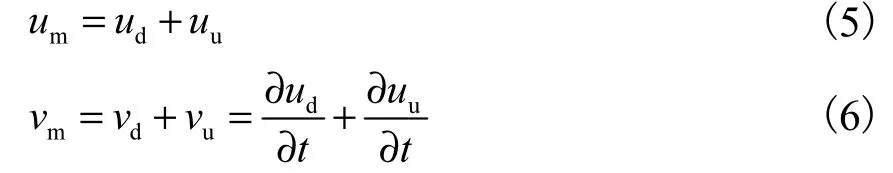
式中：uu为上行波引起的质点位移；ud为下行波质点位移；vd为下行波质点速度；vu为上行波质点速度．

此外，上、下行波满足

式中：Z为桩身截面阻抗，Z＝ρAc，ρ为桩的质量密度，A为桩底截面积，c为桩身纵波波速．

联立式(1)和式(2)，并代入式(3)～(8)中的参数关系，可得到

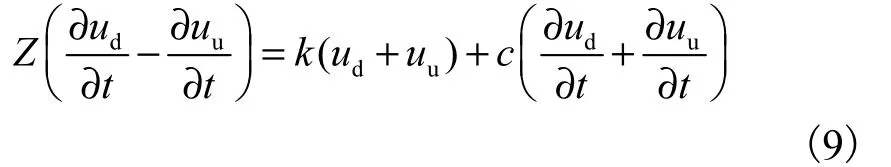
将式(9)整理得到

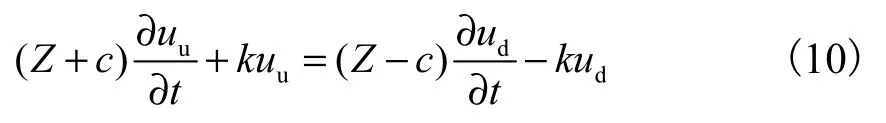
上式的左右两侧分别仅与上、下行波质点位移有关．用Uu和Ud分别表示uu和ud的傅里叶变换结果，对式(10)两边进行傅里叶变换得到

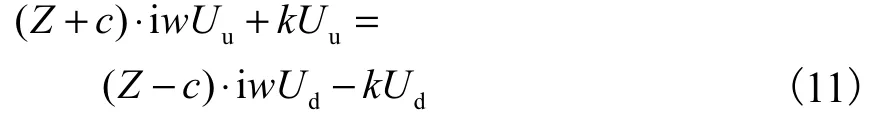
式中：i 为虚数单位；w为傅里叶变换参数，此处表示信号振动频率．

若将下行波位移ud作为输入，上行波位移uu作为输出，则两者之间的关系在频域中的表达式为

式中Hu(w)也可称为桩底截面反射波的位移频率响应函数，分母实数化后可得

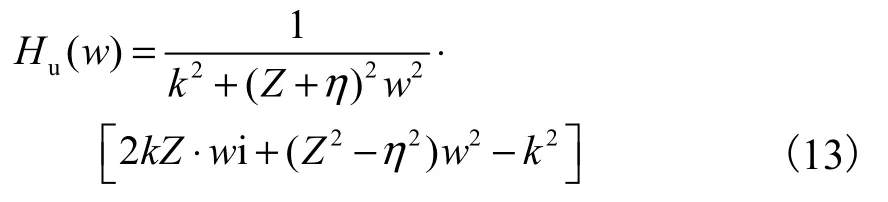
Hu(w)实际上描述了波在桩-桩底土界面的反射特性，当给定下行速度波位移(输入)后，即可根据Hu(w)得到上行速度波位移(输出)．

需要特别说明的是，本文中的Hu(w)与以往桩基纵向振动研究中的桩顶位移频响函数(以下称桩顶频响函数)不同．桩顶频响函数是桩顶位移(输出)与激振力(输入)的比值，描述的是桩土系统的综合动力特性，实际上包含了桩、桩侧土和桩底土的信息.Hu(w)则是上行速度波位移(输出)与下行速度波位移(输入)的比值，描述的是桩底的界面性质和桩底土的性质．在桩身材料和尺寸一定的条件下，Hu(w)仅描述了桩底土的性质，这为定量判断桩底支撑条件提供了可能．

由于速度信号在低应变检测中更为常用，式(14)给出了桩底速度频响函数Hv(w)．此时下行波的质点速度vd作为输入，上行波质点速度vu作为输出．

式中F[]⋅ 表示傅里叶变换．上式说明，桩底处速度频响函数与位移频响函数相同．此外，需要说明的是，桩身截面阻抗比可以反映桩身速度的反射特征，这与桩底截面速度频响函数类似，因此理论上可将桩底土的等效阻抗求解出来，等效阻抗对于直接定量判断桩底条件有一定帮助．

同样地，将下行力波Pd看作输入，上行力波Pu看作输出，结合式(7)和式(8)可得到力波的频响函数为

式(15)说明，桩底力波频响函数与位移、速度频响函数相差了一个负号．

1.2 桩底反射幅值与相位

由于力波、位移频响函数与速度频响函数表达式相似，而工程上对速度信号的应用更为广泛，以下重点讨论桩底速度频响函数Hv(w)．Hv(w)可写为

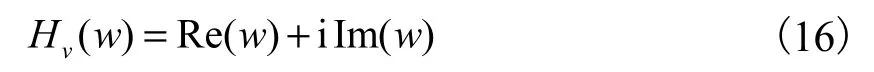
式中：Re(w)为频响函数的实部，Im(w)为频响函数的虚部．结合式(13)可知

若令∣Hv(w)∣表示速度频响函数的模，φ(w)表示输入与输出间的相位差，那么

1.3 特殊桩底的反射特征

上文将下行波作为输入、上行波作为输出，推导了波在桩底截面处引起质点的位移、速度和力的频响函数，并获得反射波和入射波间的幅值比和相位差，以下对特殊桩底条件下的速度反射特性进行分析，分析结果可对速度频响函数进行验证．

(1) 当η＝0，k＝0 时，由图2 可知，桩底支撑退化为自由边界．根据式(19)和式(20)，得到

因此，桩底为自由端时，桩底截面处质点的反射速度与入射速度大小相等、方向相同，这与以往的认识一致．

(2) 当η＝Z时，即桩底土阻尼与桩的阻抗相等时

当k远小于2Zw，或k值较小时，Hv(w)→0，φ(w)→0.5 π，此时桩底无反射．这从理论上解释了在桩基低应变检测的实际工程中，即使桩长较短，也有时出现桩底反射信号不明显的现象．这可能是桩底土阻尼与桩的阻抗恰好匹配造成的．

(3)k→+∞时，桩底边界退化为固定边界，由式(19)和式(20)也容易得到

因此，桩底为固定边界时，桩底截面处质点的入射速度与反射速度大小相等、方向相反，这也与以往的认识一致．

以上3 种特殊桩底条件下，反射速度与入射速度之间的关系，一定程度上表明桩底速度频响函数推导结果的正确性．

2 一般约束下的桩底反射特征

对于一般情况下的桩底约束条件，即k≠0 且η≠0 时，桩底反射特性研究可基于傅里叶逆变换方法并结合MATLAB 编程来完成．

2.1 验证MATLAB程序

假设下行波质点速度vd为一半正弦脉冲，如图3所示，vd的表达式为

式中：v0为下行波速度的振幅，取1 m/s；T0为正弦速度波周期，取π/400 s；t为时间．

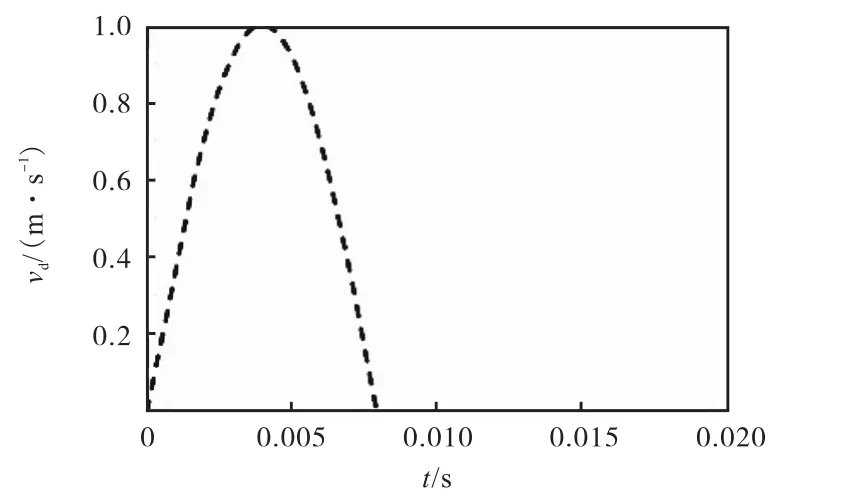
图3 半正弦脉冲形式的下行速度Fig.3 Downward velocity in the form of semi-sinusoidal impulse

桩底为特殊约束条件下，即自由端、固定端以及桩底土和桩身阻抗匹配3 种条件(①k＝0，η＝0；②k＝1×104，η＝Z＝8.8×106；③k＝η＝1×1010)，分别对应桩底自由、阻抗匹配和桩底固定3 种边界，桩底截面处下行波速度为式(24)中的半正弦脉冲时，利用MATLAB 程序计算得到的上行波速度时程曲线如图4 所示．上行波速度曲线的峰值与第1.3 节中的理论值相同，计算程序得以验证．

2.2 一般支撑下的桩底反射特征

按混凝土基桩的工程经验采用如下参数进行分析：桩径r＝0.5 m，桩长l＝10 m，纵波波速c＝4 500 m/s，桩身密度ρ＝2 500 kg/m3，弹性模量E为30 000 MPa．为简便计算，下行波速度的半正弦脉冲峰值v0取为1 m/s．此外，为研究桩底反射特征的普遍规律，定义了无量纲刚度系数k′和无量纲阻尼系数η′，反映桩底土的支撑条件，即

式中：k为桩底土刚度系数，反映了在桩底土的整体刚度；k′则是分布式桩底土相对刚度；同样地，η为桩底土的绝对阻尼系数，η′则为相对阻尼系数；A和Z分别是桩底截面面积和桩身阻抗．采用无量纲系数k′和η′进行研究，以消除桩身材料和尺寸带来的影响，从而得到更为普遍的桩底反射规律[22]．

1)η′＞1

上行波速度时程曲线的方向始终与下行波速度曲线方向相反，且仅有一个负波峰，波峰绝对值随η′的增大而增大．如图5 所示，当k′＝0.001 时，上行波速度时程曲线随η′(η′＞1)变化的情况．

图6 给出了不同k′值条件下，不同η′值对上行波速度峰值的影响．可以看出：①对于某一确定的η′，负波峰绝对值随k′的增大而增大，但当k′＞10 或k′＜0.01 时，速度峰值几乎不受k′的影响；②对于某一确定的k′，负波峰绝对值随η′的增大而增大，但当η′＞100 或k′＞10 时，速度峰值均接近-1 m/s，不受k′和η′的影响．

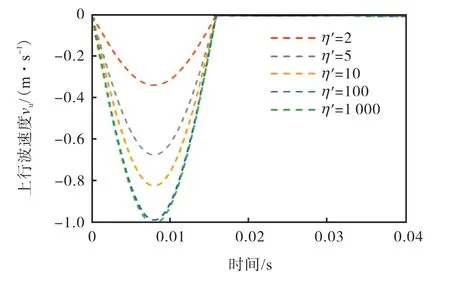
图5 vu 随不同η′(k′＝0.001，η′＞1)的变化情况Fig.5 Variation of vu with different η′ when k′＝0.001 and η′＞1

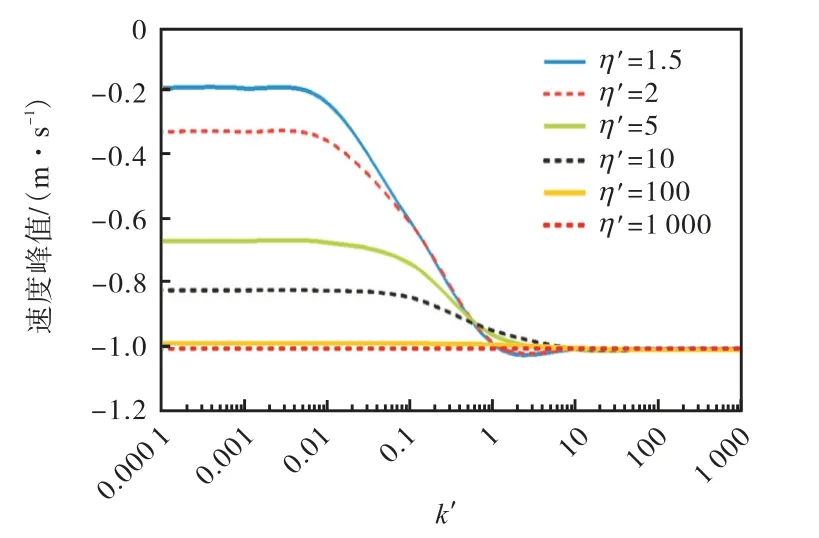
图6 vu 峰值随η′和k′的变化情况(η′＞1)Fig.6 Variation of vu peak with different η′ and k′ when η′＞1

图7 vu 随不同η′(k′＝0.001，η′＜1)的变化情况Fig.7 Variation of vu with different η′ when k′=0.001 and η′＜1

2)η′＜1

与情况(1)不同，当η′＜1 时，上行波速度时程曲线的方向和波峰数量受k′值的影响很大，具体表现为：①k′较小时，即k′≤0.01 时，上行波速度时程曲线始终与下行波速度的方向相同，仅有一个向上的正波峰，且速度峰值随η′的增大不断减小．图7 给出了当k′＝0.001 时，上行波速度时程曲线随η′(η′＜1)变化的一种情况；②k′较大时，即k′≥10 时，上行波速度时程曲线始终与下行波速度的方向相反，仅有一个向下的负波峰，且速度峰值均近乎为-1 m/s，此时桩底支撑可看作固定端；③当0.01＜k′＜10 时，上行波速度时程曲线有一个正波峰和一个负波峰，正波峰随η′的减小而增大，负波峰的绝对值也随η′的减小而增大．图8 给出了当k′＝0.1 时，上行波速度时程曲线随η′(η′＜1)变化的一种情况．

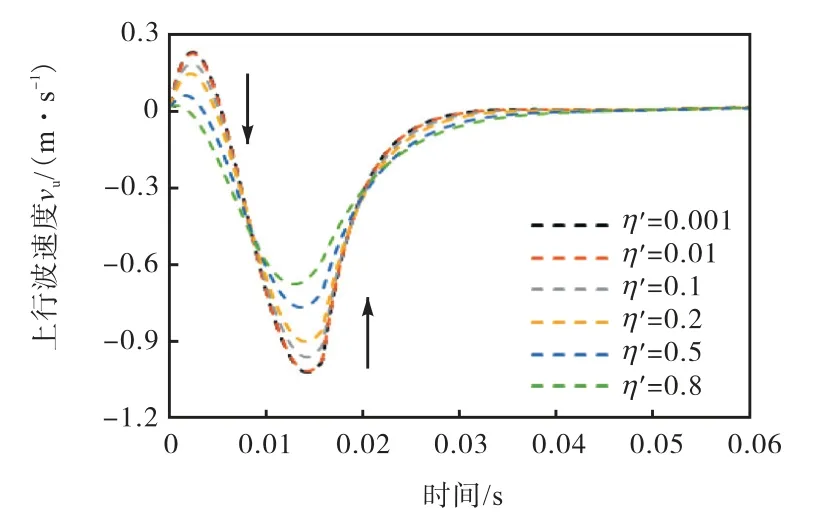
图8 vu 随不同η′(k′＝0.1，η′＜1)的变化情况Fig.8 Variation of vu with different η′ when k′＝0.1 and η′＜1

3) η′＝1

与情况(1)、(2)均有所不同，当η′＝1 时，也即桩身阻抗和桩底土阻抗恰好匹配时，上行波速度时程曲线的形状受k′值的影响较大，表现为：①k′≤0.01 时，桩底无反射波；②k′≥10 时，上行波速度与下行波速度的方向相反，仅有一个向下的负波峰，且速度峰值均近乎为-1 m/s，此时桩底支撑也可看作固定端；③k′介于0.01～10 之间时，上行波速度时程曲线仅有一个负波峰，负波峰的绝对值随k′的增大而增大，如图9 所示．

综上所述，在下行波入射速度vd为半正弦脉冲激励条件下，上行波速度vu时程曲线的形状和波峰数量由桩底土相对刚度k′和相对阻尼η′共同决定．当桩底支撑条件由自由端逐渐过渡到固定端时，上行波速度(反射波速度)与下行波速度(入射波速度)也由完全的同向相等逐渐过渡到完全反向相等．上行波速度vu时程曲线特征与k′、η′的关系汇总于表1．

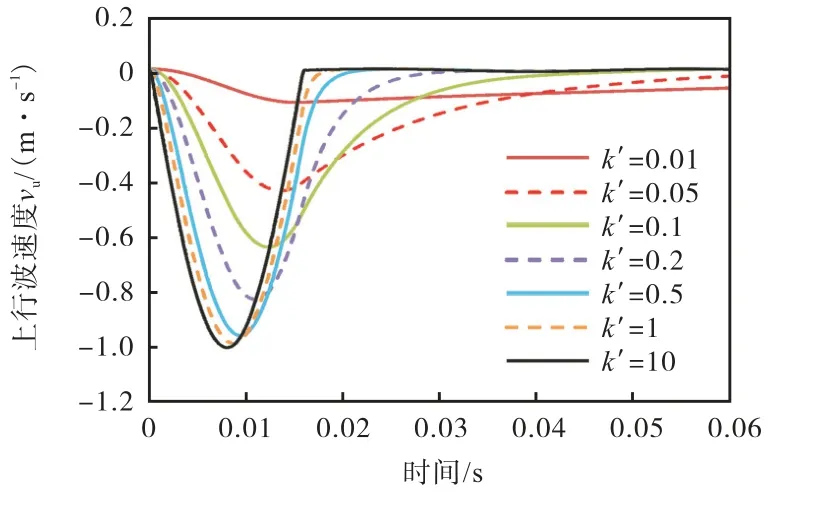
图9 vu 随不同k′(η′＝1)的变化情况Fig.9 Variation of vu with different k′ when η′＝1

表1 k′、η′与上行波速度vu 时程曲线的关系Tab.1 Influence of k′ and η′ on the characteristics of vu curves

图10 3种不同桩底支撑条件Fig.10 Pile tip with three types of support conditions

3 模型试验

3.1 试验材料和原理

采用模型试验验证不同桩底支撑条件下的桩底界面反射的理论计算结果，即应力波传播到桩底截面时，由于桩土性质差异引起的反射现象，因此不能考虑桩侧土的作用．考虑到桩底附近桩侧土的存在，一方面会对桩端加速度传感器、应变片等装置的安装测量造成干扰，另一方面桩侧土的存在会对桩底-土界面反射的真实特性造成干扰，因此试验所用模型桩未埋入土中，而是直接置于不同刚度的支撑面上．

利用尼龙棒模拟基桩进行试验，桩底支撑分别为室内混凝土地面、模型箱内松砂表面以及室外天然土面3种条件，分别模拟桩底刚度较大(k′≥10)、刚度较小(k′≤0.01)以及桩底刚度介于两者之间(0.01＜k′＜10)3 种桩底条件，见图10．利用静载试验获得桩端土体的刚度系数，利用动载试验获得桩端实测速度和轴力，并计算桩底截面处的上行波速度和下行波速度，以验证理论计算结果．

试验相关的主要材料和设备如下：尼龙棒长30 cm 和70 cm 各一根，特制可拆卸内径为80 cm 带平板的铁环一个，精度0.01 mm 的百分表一只，压电式加速度传感器两个，应变片4片，电桥盒一个以及电荷放大器、应变放大器、KD6000 采集分析仪等若干设备．尼龙棒的相关参数见表2．

表2 尼龙棒的相关参数Tab.2 Relevant parameters of the nylon rod

3.1.1 静载试验

静载试验的目的是测量桩端土体的刚度系数，试验装置如图11 所示．采用长30 cm 的短桩来保证加载稳定，通过分级加载得到桩端处的力-位移曲线，其中桩端位移通过百分表获得，桩端轴力为加载重物的重量，力-位移曲线初始直线段的斜率即为桩端土的刚度系数k，利用式(25)得到无量纲刚度系数k′．

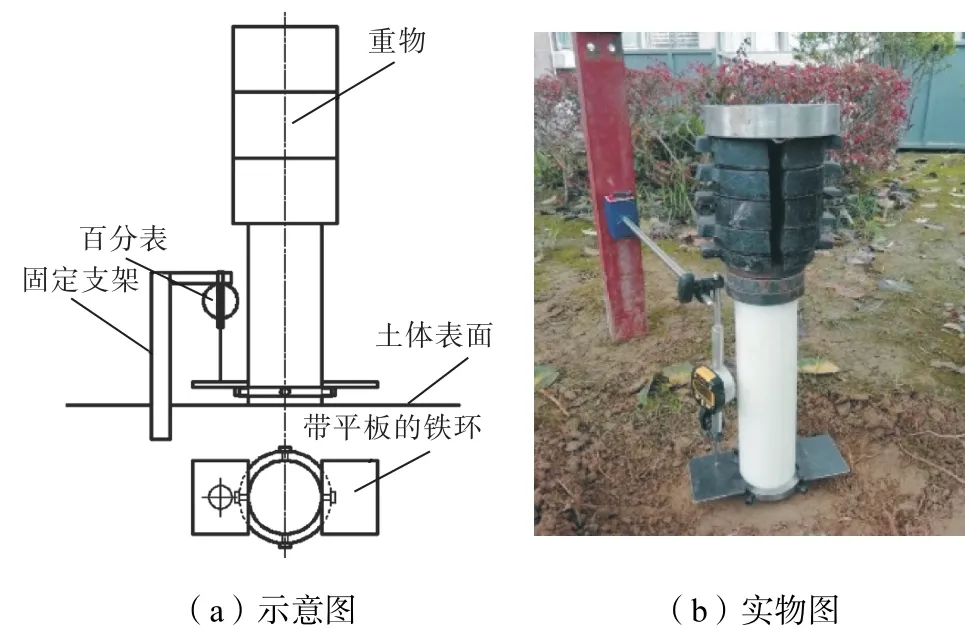
图11 静载试验装置Fig.11 Device for static experiment

3.1.2 动载试验

动载试验的目的是验证不同桩底条件下上行波速度和下行波速度时程曲线的关系．动载试验装置见图12．采用长70 cm 的模型桩来进行试验，利用小铁锤轻敲桩顶，通过桩底处的加速度传感器来测量桩端加速度，对加速度一次积分得到桩端速度．4 片应变片粘贴在距离桩底截面2 cm 处，通过电桥盒全桥连接，获得桩顶受锤击时的桩端应变并计算得到轴力.

根据桩的一维波动理论[15]，桩端截面处的上行波速度与下行波速度分别为

式中：vu(t)为任意时刻t 的上行波速度；vd(t)为任意时刻的下行波速度；v(t)为任意时刻t 桩端速度；F(t)为桩端总阻力；Z 为模型桩桩身阻抗．

图12 动载试验装置Fig.12 Device for dynamic experiment

3.2 试验结果分析

3.2.1 刚度系数

图13 给出了不同桩底条件下的静载试验的典型试验结果，桩端土体的轴力-位移曲线的初始直线段斜率的倒数即为刚度系数，不同桩底条件下取3 次静载试验结果平均值作为最终的刚度系数．

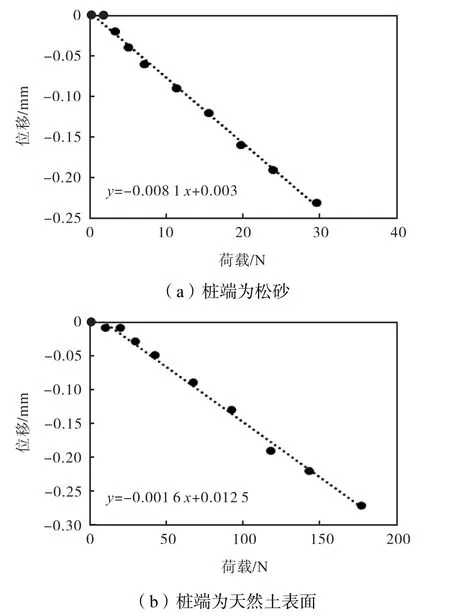
图13 静载试验中桩端荷载-位移曲线Fig.13 Relationship between displacement and load in static experiment

其中，桩端为模型箱中的砂土面时，桩底刚度系数为123.5 N/mm，换算为桩土相对刚度系数k′为0.007 2，此时k′＜0.01；桩端为天然土面时的刚度系数为652.2 N/mm，换算得到k′为0.032 2，k′在[0.01，10]范围内；桩底为混凝土地面时，桩端位移太小无法测量，容易确定桩底k′＞10．

3.2.2 动载试验结果

在动载试验中，桩顶受到一次敲击后，可获得桩端轴力、加速度时程曲线，一次典型试验结果如图14和图15 所示，加速度经过一次积分得到速度时程曲线见图16，速度方向以向上为正．不同支撑条件下的轴力、加速度时程曲线稍有不同，限于篇幅这里仅给出桩底支撑为天然土表面的一次试验结果．

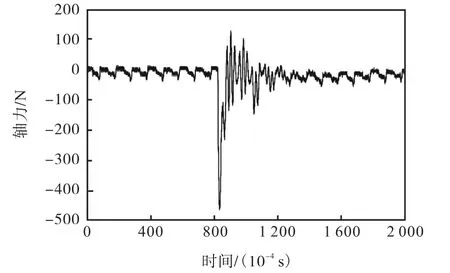
图14 桩端轴力时程曲线Fig.14 Time history curve of axial force at pile tip

图15 桩端加速度时程曲线Fig.15 Time history curve of acceleration at pile tip

图16 桩端的速度时程曲线Fig.16 Time history curve of velocity at pile tip

3.2.3 上行波速度验证

根据式(29)和式(30)，结合桩端实测速度和实测轴力，可以对桩端的下行波速度和上行波速度时程曲线进行分解．需要指出的是，由于锤击产生的速度入射波不是一个绝对的半正弦激励，这里选择速度曲线中第一次波峰位置附近(红色圈)曲线进行上、下行波的分解，并对实测下行波速度vd进行正弦拟合，利用拟合曲线作为输入对上行波速度曲线vu的理论结果进行验证．

以下对各桩底支撑条件下的试验结果进行分析，首先比较实测vd曲线和vu曲线，判断是否符合表1中理论分析的规律；然后将实测vd进行正弦曲线拟合，将拟合曲线作为输入，代入已有MATLAB 程序中，得到理论vu并与实测vu作比较，同时得到出桩底土的相对阻尼系数η′．可以得到，3 种桩底条件下的理论vu曲线预测结果与模型试验结果较为吻合．具体如下．

(1) 图17 和图18 分别是桩底为混凝土地面时，实测vd曲线和正弦拟合结果，以及实测vu曲线和理论计算结果．桩底为混凝土地面时，实测vu和vd反向，峰值大小近乎相等．若按k′＝100(桩底刚度太大，无法获取准确k′值)来进行理论计算，当η′＝8.4时，vu的理论曲线与实测曲线较为吻合，结合表1 也可看出这与理论分析的结果一致．

图17 桩底为混凝土面时vd 实测值和正弦曲线拟合结果Fig.17 Measured and sine fitting values of vd for concrete pile tip

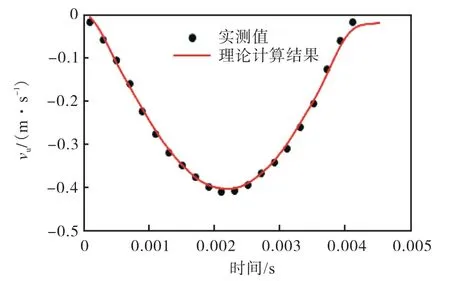
图18 桩底为混凝土面时vu 实测值和理论计算结果对比Fig.18 Measured and theoretical values of vu for concrete pile tip

(2) 图19 和图20 分别是桩底放置于模型箱中的砂土表面时，实测vd曲线和正弦拟合结果，以及实测vu曲线和理论计算结果．桩底支撑为模型箱砂土时，桩底土k′＜0.01，试验结果表明实测vu和vd同向，这符合η′＜1 的理论结果．按静载试验中桩底土k′＝0.007 2 来进行理论计算，当η′＝0.15 时，vu的理论曲线与实测曲线较为吻合．

(3) 图21 和图22 分别是桩底放置于天然土面时，下行波实测速度正弦拟合结果和上行波实测速度及理论计算结果．桩底放置于天然土面时，桩底土0.01＜k′＜10，试验结果表明实测vu具有一个正波峰和一个负波峰，结合表1 可以看出这符合η′＜1 的理论结果．按静载试验中桩底土k′＝0.032 2 来进行理论计算，当η′＝0.42 时，vu的理论曲线与实测曲线较为吻合．

图19 桩底为松砂时vd 实测值和正弦拟合结果Fig.19 Measured and sine fitting values of vd for loose sand support

图20 桩底为松砂时vu 实测值和理论计算结果对比Fig.20 Measured and theoretical values of vu for loose sand support

图21 桩底为天然土面时vd 实测值和正弦拟合结果Fig.21 Measured and sine fitting values of vd for natural soil surface

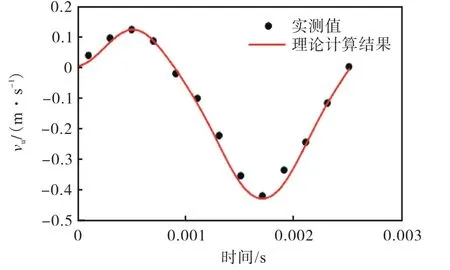
图22 桩底为天然土面时vu 实测值和理论计算结果对比Fig.22 Measured and theoretical values of vu for natural soil support

4 工程应用初步探讨

由工程实践可知，在桩基低应变完整性检测中，敲击桩顶得到的实测速度信号一般为一“钟形”脉冲，上、下行波速度信号可采用半正弦函数拟合，且拟合效果一般较好．在桩基施工完成后，利用桩身预留小孔，例如声测孔或预制管桩的中心孔等，可将多个加速度计沿不同深度固定在桩壁上，用于获取不同位置处的桩身速度信号，如图23 所示．

图23 桩底条件定量化检测示意Fig.23 Schematic diagram of quantitative determination of pile bottom condition

通过一次低应变敲击，获得沿桩身不同深度的速度信号，在相对远离桩底的位置，实测速度信号即为下行波速度信号；在靠近桩底的位置，实测速度信号为下行波和上行波的叠加．利用远离桩底的下行波速度信号，可拟合出沿桩身速度峰值的衰减曲线，从而得到桩底截面的下行波速度，进而结合桩底实测速度信号即可得到上行波速度．根据本文推导的上、下行波速度峰值的相对大小与桩底相对刚度、阻尼之间的关系，即可对桩底支撑条件作定量判断．根据初步研究结果，桩身下行波速度信号沿桩身的衰减规律，呈现强烈的指数曲线形式，相关研究成果限于文章篇幅将另文讨论．

通过定义桩底截面处上行波速度(反射速度)与下行波速度(入射速度)之间的关系，实现桩底条件的定量化检测，不破坏桩体本身，也可消除传统低应变检测方法桩侧土阻尼、桩身阻尼对行波衰减的影响，可成为一种方便可靠的桩底条件检测和判断方法.但在实际工程应用方面还需要进一步研究，包括：①桩底土的刚度和阻尼之间的关系对桩底反射的影响；②需要研究制定桩底支撑条件的定量标准；③如何准确方便地实现桩底加速度或速度的测量．

5 结 论

本文推导了桩底截面的行波频响函数，研究了低应变条件下桩底界面处的上、下行波速度之间的关系，重点探讨了在半正弦脉冲激励和黏弹性支撑模型下，上行波速度曲线在不同桩底土刚度、阻尼下的变化规律．研究成果提供了一种实现上、下行波分离的理论方法，可用于消除行波叠加干扰，同时具有定量判断桩底条件的潜在工程价值．所得到的主要结论如下：

(1) 桩底反射特征仅与桩底行波频响函数有关，桩底速度频响函数与位移频响函数相同，与力波频响函数相反．利用桩底反射特征和频响函数，可避免行波衰减对桩底条件检测的影响．

(2) 桩底截面处上行波速度曲线(vu)的形状、方向和波峰数量受桩土相对刚度系数k′和相对阻尼系数η′共同影响；桩底条件由完全自由端过渡到完全固定端时，vu曲线和vd曲线的关系也存在一个过渡，两者由等值同向逐渐过渡到等值反向．

(3) 桩底vu曲线的变化规律具体表现为：当η′＜1 时，随着k′的增大，vu曲线由同向单峰，过渡到具有一个正波峰和一个负波峰，最后变为反向单峰；当η′＝1 时，随着k′的增大，vu曲线由无反射波，过渡到反向单峰；当η′＞1 时，随着k′的增大，vu曲线始终为反向单峰，且单峰峰值的绝对值随k′的增大而增大．