循环荷载作用下软黏土累积塑性应变与微观参数灰色关联分析

2021-01-11雷华阳张雅杰冯双喜孙晓芳蒋明镜

天津大学学报(自然科学与工程技术版) 2021年3期

雷华阳，张雅杰，冯双喜，孙晓芳，郝琪，蒋明镜

(1. 天津大学建筑工程学院，天津 300354；2. 天津市滨海土木工程结构与安全教育部重点实验室，天津 300354；3. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室，天津 300354)

长期以来，人们主要基于宏观或者唯象层面描述软黏土的非连续性、大变形和破坏等复杂特性．研究发现，软黏土在宏观上表现出的变形、破坏等工程特性是内部微观结构的具体表现，其宏观性质在一定程度受到微观参数的影响，宏观参数和微观参数相互影响．因此，系统开展软黏土宏观变形与其微观参数的关联性研究，对于从根本上认识并解决软黏土岩土工程灾害问题具有重要的理论意义和实用价值．

国内外学者基于波浪荷载、交通荷载、地震荷载和机械振动等动力荷载的振动方式对软黏土变形特性开展了大量细致的试验研究．其中，软黏土的累积塑性应变是极为重要的宏观指标．比如，Hyodo 等[1]对饱和软黏土进行了循环荷载试验，通过使用相对循环应力比的新概念，提出了一种可用于预测残余累积塑性应变的新型计算模型．浙江大学郭林等[2]通过不排水动三轴试验对温州天然软黏土进行累积塑性应变特性研究，分析了循环振动次数、围压对结构性软黏土累积塑性应变的影响规律．黄茂松等[3]建立了可以同时反映等向、偏压固结不排水的累积塑性变形预测模型，并通过一系列动三轴试验验证了模型的合理性．沈扬等[4]利用空心圆柱扭剪仪进行了不同主应力轴旋转应力路径下的试验．研究了临界动应力比影响下的软黏土累积塑性应变的变化规律．郑刚等[5]通过对天津临港工业区典型软黏土的一系列动力试验，发现循环荷载作用下，原状土的累积塑性应变曲线随振动频率的增加由破坏型向发展型再向稳定型逐渐变化．

扫描电子显微镜(SEM)和压汞法(MIP)等新兴技术已广泛使用于对软黏土的孔隙分布和颗粒形态等的观测研究．Moore 等[6]通过对砂性土的微观图形进行分析，得出了砂性土具有明显的分形特征，通常分形维数的数值在1～2 之间．Warr 等[7]使用基于SEM 图像的计算机分析方法对断层的软黏土进行了观察，研究了其微观性质．施斌等[8]运用图像分析软件对软黏土微观结构特征进行了深入的分析研究，指出颗粒各向异性、矿物成分等是表征软黏土微观结构特征的具体指标．王清等[9]通过SEM 图像处理软件，研究得到软黏土微观结构中土单元的形态、定向性、孔隙特征等结构要素的定量评价指标．Lei 等[10]通过MIP 和SEM 试验，研究了软黏土三轴蠕变试验条件下微观结构、粒径大小和孔隙分维等参数的变化，解释了加速蠕变的机理．张中琼等[11]对土样微观结构、颗粒粒度、颗粒丰度、颗粒定向性以及宏观基本物理性质变化进行分析，提出颗粒定向性和丰度的增加可以促使黏土颗粒团聚．

不同软黏土特有的宏观复杂特性本质上受控于微观结构特性及其演化，基于连续介质力学和唯象思想的传统岩土力学理论，在描述复杂软黏土的非连续性、破坏、颗粒运移、颗粒破碎、组构演化等问题上陷入瓶颈，难以揭示复杂问题的深层机理，进而极大限制了岩土工程实践水平．目前，在以微观揭示宏观特性方面已获得了较多的研究成果．Thornton[12]采用离散元方法(DEM)第一次验证了土力学中的强度理论，研究了土的宏微观特性之间的联系，开启了宏微观土力学的新篇章．唐益群等[13]通过研究软黏土宏观变形与微观结构之间的相关性，发现软黏土微观参数在临界值前后变化较为明显．李顺群等[14]使用统计学中的相关分析和主成分分析的方法研究了软黏土微观参数和宏观力学性质之间的联系．莫海鸿等[15]采用Davidenkov 三参数模型和微观孔隙结构参数计算相结合的方法，对重塑软黏土动剪切模量与土颗粒孔隙特性进行了关联分析．Mitaritonna 等[16]通过SEM 试验对土体小应变条件下的各向异性进行机理分析，证明了宏观的各向异性可归因于微观颗粒的定向性特征.

目前，土体微观试验研究多以描述宏观特性的变化现象为主要内容，无法从微观动态过程揭示软黏土宏观特性的机理．同时，对于宏观累积塑性应变的微观变形机理研究尚未完善．基于此，本文开展了一系列宏观试验和微观试验，分析天津软黏土的累积塑性应变的变化规律；揭示平均粒径、颗粒分维、孔隙分维、颗粒定向概率熵、平均孔径等土体微观参数的变化规律，建立累积塑性应变与微观参数灰色关联度，明确其关联特征分析，研究结果为宏微观土力学研究提供数据参考．

1 试验土样及试验方案

1.1 试验土样

试验土样取自天津滨海新区某工程现场，取土深度为5～15 m，采用薄壁取土器取样．参照《土工试验方法标准》(GB/T 50123—2019)中的相关内容进行土样的物性参数测试，土样的粒径级配曲线如图1所示，其中黏粒和胶粒含量占52.98%．土样的X 射线衍射结果分析如图2 所示，土样的主要矿物成分是石英、高岭石和蒙脱石等．土样基本的物理力学参数如表1 所示．

图1 软黏土颗粒级配曲线Fig.1 Grain size distribution curve of soft clay

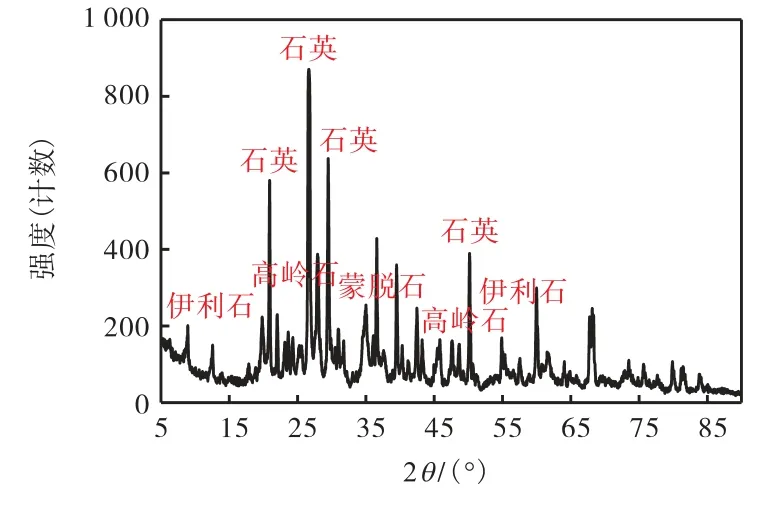
图2 X射线衍射分析Fig.2 Results of X-ray diffraction analysis

表1 土样基本物理力学参数Tab.1 Basic physical and mechanical parameters of soil samples

1.2 试验方案

列车动荷载主要是由移动列车在轨道上的重力加载形成，对于城市地铁，车速低于100 km/h 时，其主要频率在10 Hz 以下[17]．唐益群[18]通过现场监测得到列车以30～40 km/h 低速进站的振动频率统计值为2.40～3.05 Hz，而国内地铁正常行驶时速一般为80 km/h，频率应在4～6 Hz 之间．张勇等[19]在饱和重塑软黏土不排水动三轴试验中采用4 Hz 的正弦波模拟列车荷载．很多复杂的波形曲线经过傅里叶变换能用正弦加载来代替，正弦加载产生的效果和复杂加载效果接近．曹勇等[20]提出交通荷载对软土地基的循环作用可等效成三角形或正弦波形，当幅值小于临界应力时，波形对软土变形的影响不大．为了实现列车动荷载对软黏土累积塑性应变的影响，本文选取4 Hz 的正弦波进行试验研究．

动三轴试验采用英国GDS 公司生产的ELDyn标准型动态三轴试验机．试验首先依据土工试验规程对天津软黏土原状土进行制样，将原状土制作为6 个直径39.1 mm、高度80 mm 的圆柱形试样，用保鲜膜包裹土样侧面，滤纸覆盖圆柱土样上下表面，装入内侧涂抹凡士林的三瓣膜中进行真空饱和．土样饱和完成后进行B值监测．当B值不小于0.95 时土样完全饱和．其次，根据取土深度15 m、土的重度17 kN/m3及侧压力系数0.43，选取围压cσ＝100 kPa 的条件下对土样进行排水固结，以孔压消散达到95%以上作为固结完成的标准．最后，对其中的5 个试样进行不排水循环动三轴试验．为使变形充分发展，微观结构具有可区分度，选取较大的动应力比CSR＝0.3，则动应力幅值dσ＝60 kPa．进行三轴试验时，对5 个土样分别施加频率f为4 Hz，振次N分别为200 次、500次、1 000 次、5 000 次和10 000 次的正弦波．

图3 IPP软件处理后的SEM图像Fig.3 SEM image processed by IPP software

结合扫描电子显微镜(SEM)和压汞法(MIP)两种试验手段进行微观结构测试分析．本试验选用LEO 1530 VP 型场发射扫描电镜和AutoPore IV 9500 V1.05 型压汞仪．SEM 和MIP 试验的试样制备分为4 个步骤：①使用轴向侧向同时卸荷的方法进行卸样，减小卸荷对微观结构的影响[21]．选取累积塑性应变发展集中的部位切削成两种尺寸的试样：一种尺寸为1.5 cm×0.8 cm×0.8 cm(SEM 测试)；另一种尺寸为1 cm×1 cm×1 cm(MIP 试验)．②将土样放入液氮罐密封冷冻30 s 以上使其快速冻结，试样中的水分直接转变为非晶体固态水．③取出土样进行真空干燥，土样中固态水直接升华为气态水．试样结构达到了干燥状态，原结构被保存．④真空干燥24 h 后取出试样．将第一种尺寸的土样掰断，选取较为平整的断面用作SEM 试验，第二种尺寸的试样可直接用作MIP 试验．使用Image-Pro Plus(IPP)软件对SEM 图像(见图3)进行处理，本文的灰度直方图为单峰状图像，已有研究认为当拖动范围限制条设在峰值的80%左右时能达到最好的分割效果[22]．对于软件无法精确处理的颗粒，通过采用软件中人工分割的功能将冗杂颗粒分开，同时补足颗粒缺失部分后再进行IPP 数值统计分析[23]．通过IPP 软件计算得出平均粒径、面积分形维数及颗粒定向概率熵．通过MIP 试验结果对孔隙大小和分布进行定量化分析．

2 试验结果分析

2.1 累积塑性应变

图4 是累积塑性应变发展随振次N的变化曲线．在整个发展过程中，累积塑性应变增量随振次N的增加呈现先线性增长后缓慢增长并持续降低直至稳定到零的特点．土样的累积塑性应变过程分为3 个阶段．第Ⅰ阶段是振动前期，累积塑性应变随着振次N的增加成线性增加．振次N达到500 次时，土样的累积塑性应变为 0.28%，占总累积塑性应变的50.91%；第Ⅱ阶段是振动中期，即500＜N≤5 000时，累积塑性应变的增加速率逐渐降低，呈现减速增加的状态，在此阶段，累积塑性应变发展至0.53%，占总累积塑性应变的96.36%；第Ⅲ阶段是振动后期，即5 000＜N≤10 000 时，累积塑性应变增长较小，应变整体接近稳定值0.55%．

图4 累积塑性应变随振次N 的变化Fig.4 Cumulative plastic deformation changes with the number of vibration N

累积塑性应变的实质是动荷载作用下处于平衡状态的土体受力改变造成应变变化，微观上看是由于土体内部的颗粒重组和土颗粒间的相对滑移所致．加载前期，土体在循环荷载作用下，土粒能够产生相对滑移，颗粒重排，塑性应变累积能量耗散，土体开始发生变形．随着振次N的增加，黏滞累积能量耗散速率将逐渐超越塑性应变累积能量耗散速率，此时土体未破坏且变形趋于稳定[24]．

2.2 平均粒径

图5(a)～(f)为原状土在振动200、500、1 000、5 000 和10 000 次后放大600 倍的SEM 图像．在图像中，土颗粒以两种不同形式存在：一种是边缘较为粗糙且尺寸较大的凝块状颗粒；一种是边缘较为光滑且尺寸较小规则片状高岭石和絮凝片状蒙脱石的团状颗粒．随着振次N的增加，土中凝块状颗粒数量逐渐减少，团状颗粒数量逐渐增加．在振动前期，颗粒的形态大小和排布发生了变化，凝块状颗粒上附着的团状颗粒开始分散，凝块状颗粒尺寸缩小．同时，平均孔径有所减小，颗粒的排列变得紧密．这是由于凝块状颗粒间相互磨擦碰撞，导致排布松散、边缘光滑，同时较小的团状颗粒在荷载作用下破碎，形成更小的黏土团粒．振动中后期，凝块状颗粒之间有明显的交错，平均孔径继续减小，破碎的黏土团粒重新聚合，黏土片之间部分恢复胶结，团状颗粒数量也显著上升．

图5 不同振次N 下放大600倍时的SEM图Fig.5 SEM image of the soil sample magnified 600 times at various values of vibration N

图6 是平均粒径随振次N的变化曲线．从图中可看出，平均粒径呈现先减小后增加的趋势．平均粒径的初始值为5.80µm，经过500 次的循环荷载作用减小至最低值3.94µm，宏观表现为累积塑性应变增加．振动中后期，平均粒径的大小随振动次数的增加而升高，振动10 000 次后，平均粒径增大至6.74µm.其原因是，振动前期时，团粒破碎，造成土颗粒尺寸缩小；振动中后期时，土颗粒间孔隙被压缩减小，分散的较小的团粒被压密组成较大的团粒，土颗粒尺寸增大．

图6 平均粒径随振次N 的变化Fig.6 Average particle size changes with the number of vibration N

2.3 面积分形维数

分形维数是表现单元体形态复杂程度的量化指标，一般使用面积-周长法[25]进行计算，其中分形维数D可由式(1)计算得出．黏性土颗粒分形维数一般取1～2．数值越小说明单元体形态的复杂程度越低，边缘较为光滑；反之则说明单元体形态的复杂程度高，边缘较为粗糙．基于式(1)对每个微观结构在面积-周长双对数坐标系下进行线性拟合得到对应的面积分形维数，其线性拟合相关性R2均在0.95～0.98 之间，不低于0.95，说明拟合效果较好．

式中：Ce为单元体等效周长；D为单元体分形维数；Ae为单元体等效面积；a为常数．

颗粒和孔隙面积分形维数随振动次数的变化如图7 所示．颗粒和孔隙分维数在振动初期有小幅度增大，然后趋于平稳，振动后期发生明显降低的情况．振动前期，颗粒分维由1.177 上升至1.203，孔隙分维由1.184 上升至1.197；振动中后期，颗粒分维下降至1.154，孔隙分维下降至1.175．颗粒和孔隙面积分维数的整体发展趋势基本相同，随振动次数的增加先增大后减小．表明在振动前期，团粒破碎，土颗粒边缘的粗糙程度增加，同时，部分孔隙被挤压，孔隙面积减小．在振动中后期，随着振动的挤密作用，团粒间重新聚合，颗粒和孔隙被持续压缩，土颗粒边缘逐渐变得光滑，其形态更为贴合．

图7 颗粒和孔隙面积分形维数随振次N 的变化Fig.7 Change in the area fractal dimension of particles and pores with the number of vibration N

2.4 颗粒定向性

由于循环荷载的持续作用，为达到新的平衡状态，土颗粒的排列方式必将做出相应的调整．因此颗粒定向性反映了土体的应力变化过程，对土体的宏观性质也有较大的影响．

图8 是在不同振次N下根据每个颗粒的主定向角绘制的玫瑰图．从图8 中可看出，开始振动前，土样颗粒具有一定的定向性，为45°和225°，振动前期，颗粒定向性减弱，趋于无定向性；振动中后期，颗粒排布趋于统一，定向性增强，为90°和270°．这是由于振动作用改变了颗粒的方向，使其由原先的无序改变为趋于一致．

图8 不同振次N 下颗粒方向模拟图Fig.8 Simulation of the direction of particles at various values of vibration N

单元排列有序性可使用颗粒定向概率熵作为微观量化指标，根据土单元在各方向位置处的定向强度，使用式(2)中的公式进行计算．Hm的取值在[0，1]之间，取值为0 时，所有土单元的排列方向完全随机，同时均布在各个方位区间内，其有序程度最低；取值为1 时，所有土单元排列方向均相同，说明土单元的有序程度最高．

式中：Hm为颗粒定向概率熵；n为方位区数；Pi为土单元在某方位区中的概率．

颗粒定向概率熵随振动次数的变化曲线如图9所示．颗粒定向概率熵在振动初期有小幅度增大，在振动中后期发生明显降低的情况．振动前期，颗粒定向概率熵由0.659 上升至0.664；振动中后期，下降至0.653．这说明经过动载后，颗粒排布方向趋于一致．由于振动挤压作用，孔隙方向一致性增强．

图9 颗粒定向概率熵随振次N 的变化Fig.9 Variation of the particle probability entropy with the number of vibration N

2.5 平均孔径

综合考虑软黏土的物性指标和MIP 试验的试验结果，将孔径大小分为5 种[26]：超微孔隙(＜0.01µm)；微孔隙(0.01µm～0.1µm)之间；小孔隙(0.1µm～1µm)；中孔隙(1µm～10µm)；大孔隙(＞10µm)．

图10 是孔径分布曲线随振次N的变化情况，其反映出单位土体中各孔径对应的实际体积．由图10可以看出，不同振次N下土体孔径分布曲线中存在两个波峰，变化范围也主要集中在小孔径到中孔径之间．由图10(a)N＝200 和N＝500 的振动过程可以看出，对应小孔径的大波峰曲线整体向左移动，波峰升高，说明在振动前期小孔隙与微孔隙的数量增加且孔径减小；对应中孔径的小波峰则基本没有变化．从图10(b)N＝1 000，N＝5 000 和N＝10 000 的振动过程中，对应小孔径的大波峰曲线发生了大幅衰减且有分化为两个波峰的变化趋势，这说明振动中后期，小孔隙的体积明显降低，且大部分的孔隙在振动挤压后其孔径变得更小；在这期间，小波峰的峰值先增加后减小，即中孔隙在颗粒重组中先短暂占优，而后还是在挤密作用下转化为更小的孔隙．

表2 为不同振次N下孔径和平均孔径变化规律表．由表2 可以看出，随着振次N的增加土体孔隙中超微孔隙、微孔隙和小孔隙所占比例上升．中孔隙所在比例下降，而大孔隙所占比例先上升后下降．平均孔径随着振次N的增加，先快速降低随后缓慢下降，直至稳定．

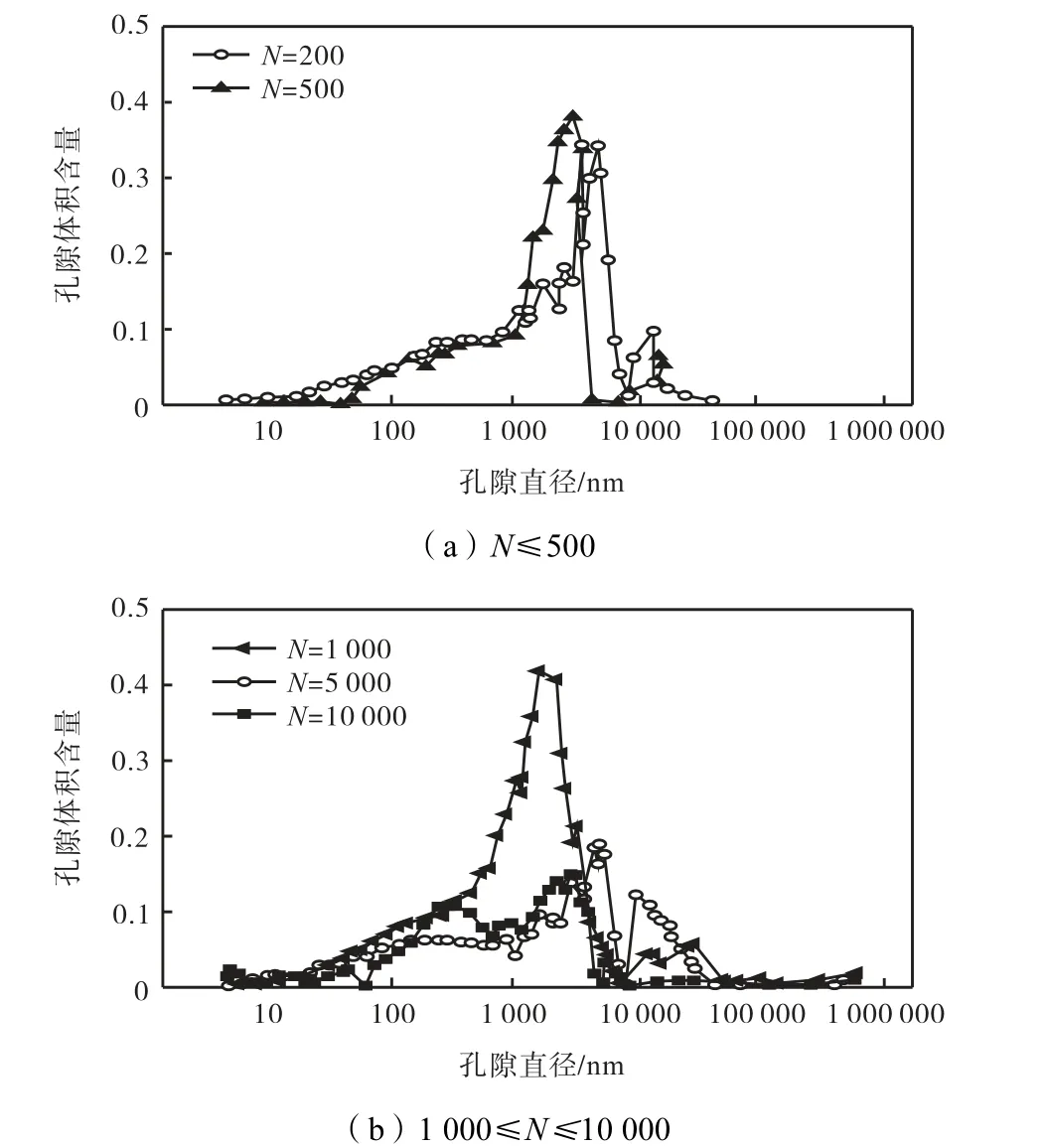
图10 不同振次N 下孔径分布曲线Fig.10 Variation of the pore diameter distribution curve with the number of vibration N

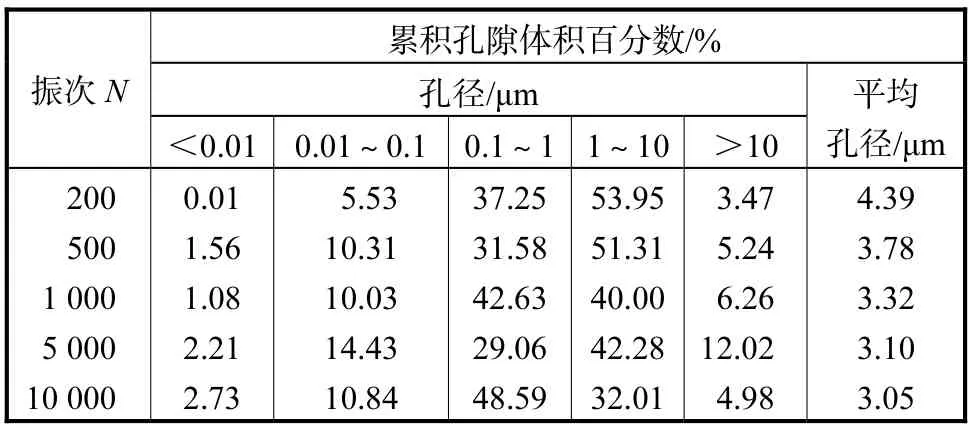
表2 不同振次N 下孔径和平均孔径变化规律Tab.2 Variation of pore diameter and average pore diameter with the number of vibrations N

3 累积塑性应变与微观参数灰色关联度和关联特征分析

3.1 灰色关联度分析

灰色关联分析的原理是在两个因素序列随其中一个变量的改变过程中，其变化程度越趋于一致，则关联程度越高，反之则关联程度越低．宏微观参数两个因素相关性的灰色关联分析步骤如下．

(1) 从微观参数的角度对宏观参数的变化进行解释，选择宏观参数累积塑性应变为参考序列X0={x0(1 ) , x0( 2 ),…,x0(n)}，微观参数为对比序列Xi={{xi(1 ) , xi( 2 ),…,xi(n )}, i=1,2,…,m}．

(2) 进行无量纲化处理．

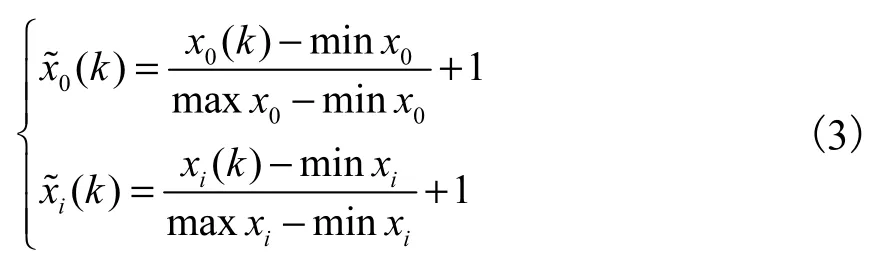
式中：max x0和min x0分别为累积塑性应变序列中的最大值与最小值；maxix 和minix 分别为微观参数序列中的最大值与最小值．

(3) 灰色关联系数ξi(k)的计算．参照应变序列，微观参数序列各个对应点的关联系数ξi(k)的计算方法如下所示：

式中：ξi(k)为两参数序列的关联系数；Δi(k )为两参数序列的接近度，两参数序列间各点的绝对差值；ρ为分辨系数．

(4) 两参数序列的关联度γi的计算．将两参数序列关联系数ξi(k)求平均值得出两个序列间整体关联程度，即关联度γi．分辨系数通常取为 0.5～0.6[27]，计算得关联度γi≥0.6 时，具有相关性．关联度越接近1，则关联性越强．

式中：γi为关联度；ξi(k)为关联系数．

针对试验中的土样分别计算宏观累积塑性应变序列和微观参数序列之间的平均关联度，如表3所示．

表3 各微观参数与累积塑性应变的平均关联度Tab.3 Average correlation between microscopic parameters and cumulative plastic deformation

从表3 中可以看出，累积塑性应变与平均粒径、孔隙分维、颗粒分维、颗粒定向概率熵和平均孔径的关联度iγ均大于0.6，表明累积塑性应变受微观土单元的大小、形状和其定向性的影响．

为保证影响因素之间的独立性，避免使用影响作用重复的参数，使用灰色关联分析法对5 个微观参数进行自相关分析．根据相关文献，若某两个参数序列之间的关联度系数超过0.8，则这两个参数的影响基本相同，须舍弃其中一个[28]．

表4 是微观参数自相关分析，汇总了5 个微观参数的两两对比的关联度．平均粒径与颗粒分维、定向概率熵之间的关联度均超过了0.8，为方便后续研究保留平均粒径，同时舍弃其余两个参数．平均孔径与其他4 个参数关联度均小于0.8，故保留．综上，累积塑性应变与平均粒径、平均孔径和孔隙分维3 个微观参数相关，平均关联度分别为0.62、0.64 和0.71．

表4 微观参数自相关分析Tab.4 Autocorrelation analysis of microscopic parameters

3.2 关联特征分析

为了考虑土体累积塑性应变与微观参数的关联特征，本文重点研究了累积塑性应变εp与平均粒径ds、平均孔径dv、孔隙分维Dv之间的关系，利用回归分析建立了关联特征表达式，如图11 所示．

通过回归分析可知，拟合程度R2均超过0.8，拟合效果良好．振动前期，εp与ds、dv和Dv分别呈现线性函数、指数函数和线性函数的关联特征；振动中后期，分别呈现对数函数、指数函数和线性函数的关联特征．具体关联特征函数表示为

式中：εp累积塑性应变；ds为平均粒径；dv为平均孔径；Dv为孔隙分维．

由图11(a)可知，振动前期，累积塑性应变εp随平均粒径ds的增加呈现减小的趋势；振动中后期，累积塑性应变εp随平均粒径ds的增加呈现增大的趋势．这是由于振动前期，土体在循环荷载作用下，平均粒径因土颗粒的分散而变小，累积塑性应变增大；振动中后期，随着振次N的增加，土颗粒重新聚合，平均粒径增大，塑性累积应变继续增大．当平均粒径ds取最大值6.74µm 时，累积塑性应变达到最大0.55%．从图11(b)中可以看出，累积塑性应变εp随平均孔径dv的增加而减小．其原因是原有土骨架的坍塌、挤压使得孔隙不断被填充和迁移，孔隙最终由大孔隙转换为小孔隙[29]．由此可以看出，平均孔径dv的大小直接反应了宏观累积塑性应变εp，其值越小在宏观上表现为土体变形越大，累积塑性应变εp变大．当平均孔径dv为3.05µm 时，累积塑性应变εp达到最大值0.55%．由图11(c)可知，振动前期，累积塑性应变εp随孔隙分维Dv的增加呈现增大的趋势；振动中后期，累积塑性应变εp随孔隙分维Dv的增加呈现减小的趋势．这是由于振动作用使得孔隙结构发生变化，随着振动挤密，孔隙被持续压缩，孔隙边缘逐渐变得光滑．这最终导致孔隙分维Dv越大，累积塑性应变εp越小．