考虑节点刚度的预制混合梁框架抗侧刚度研究
2021-01-11张锡治李星乾
张锡治 ,赵 冬,李星乾,陈 昆
(1. 天津大学建筑设计规划研究总院有限公司,天津 300072;2. 滨海土木工程结构与安全教育部重点实验室(天津大学),天津 300072;3. 天津大学建筑工程学院,天津 300072)
标准化预制构件之间高效率装配式连接方式,以及连接的可靠性和质量检测的可行性是制约装配式建筑发展的瓶颈问题.同时,由于预制构件间接缝、焊接、预埋件变形等因素的影响,装配式结构梁柱节点的半刚性特性也更加突出[1-2].国内外众多学者针对框架结构节点的半刚性特性开展了相关研究,提出并完善了框架结构考虑节点半刚性的设计理论.Frye等[3]归纳总结了钢结构不同节点构造形式所对应的M-θr关系曲线表达式,并采用割线法分析了半刚性节点的非线性特征;王新武[4]归纳总结了以往节点转角刚度计算的相关研究成果,肯定了如Frye-Morris多项式模型[3]、Kishi-Chen 幂函数模型等[5-7]一系列计算方法的实用性,提供了在实际工程中计算梁柱节点转角刚度的有效途径;蔡建国等[8]提出了预制混凝土框架梁的力学模型,同时利用位移法对框架结构的横梁弯矩和抗侧刚度进行了讨论;Chan[9]利用有限元动力学理论对半刚性钢框架进行了研究,得到了框架结构在动力荷载下的动力响应;Sucuoglu[10]定义了混凝土框架结构梁柱连接的刚度系数来描述节点处的刚度,并分别取节点刚度系数p=1.0、0.9、0.8 对一个三跨五层混凝土框架进行了分析.
为解决装配式混凝土结构中梁柱节点连接中存在的施工繁琐、现场湿作业量大等问题,张锡治等[11]提出了一种由两端钢梁和中间部分混凝土梁组合而成的钢-混凝土预制混合梁,钢梁与混凝土梁之间由栓钉、连接板和端板连接而成.相对于中间部分的混凝土梁,预制混凝土混合梁梁端的H 型钢梁一般抗弯刚度较小.预制混合梁梁端通常采用钢结构节点连接方式,相较于现浇混凝土框架,其梁柱节点连接的半刚性问题将更为突出.如果继续沿用梁柱节点刚性连接基本假定计算结构的水平侧移量,其计算结果一般将低于实际值,会给结构设计带来不可避免的潜在风险.基于以上问题,本文对预制混合梁在弹性受力阶段下的刚度矩阵进行考虑半刚性连接的相关修正,探讨考虑半刚连接下框架结构的抗侧刚度随预制混合梁钢梁长度与总长度比α、钢梁与混凝土抗弯刚度比e、结构柱线刚度i和螺旋弹簧转动刚度k变化的趋势,并建立有限元模型与理论结果对比分析.
1 考虑半刚性连接的预制混合梁刚度矩阵
1.1 计算模型及基本假定
如图1 所示,预制混合梁中部主体梁为混凝土梁,抗弯刚度为EcIc,中部混凝土梁两端为钢梁,抗弯刚度为EsIs.由文献[12]可知,在预制混合梁破坏失效之前混凝土主体梁与钢梁之间的连接区域均未发生明显破坏,预制混合梁整体受力性能较好,计算中假定钢梁和混凝土主梁为刚性连接.
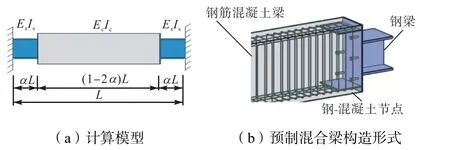
图1 预制混合梁模型Fig.1 Model of precast hybrid beam
定义

式中:α为梁长度比,0<α<0.5;e为梁抗弯刚度比;Ls为预制混合梁单侧钢梁段长度;L为预制混合梁跨度.
计算预制混合梁刚度矩阵及分析其结构抗侧刚度应满足下列3 个基本假定:①其变形是完全弹性且是线性的;②位移和形变是微小的(符合位移叠加原理);③截面应变保持平面.
1.2 梁端位移、内力关系式
假设预制混合梁边界条件为刚接,A、B为梁端节点,忽略剪切变形,则端部反力与位移之间的关系为

式中:Δ为左端较右端的相对线位移;FQAB、FQBA为梁端剪力.规定线位移以竖直向上为正,梁端弯矩MA、MB和转角θA、θB以顺时针为正,梁端剪力以使梁单元发生顺时针转动为正.
当Δ=0 时,预制混合梁两端弯矩可以表示为

为考虑连接半刚性的影响,在预制混合梁左右梁端位置加入转动弹簧,设其转动刚度均为k,固端A、B的转角为θA、θB,如图2 所示.故式(5)可以改写为

图2 半刚性连接下的预制混合梁计算模型Fig.2 Calculation model of precast hybrid beam with semi-rigid connections

此时A、B固端转角与梁端转角存在着转角差θr,A、θr,B,并有如下关系:

将式(8)代入式(7)中并以矩阵形式表示,则有
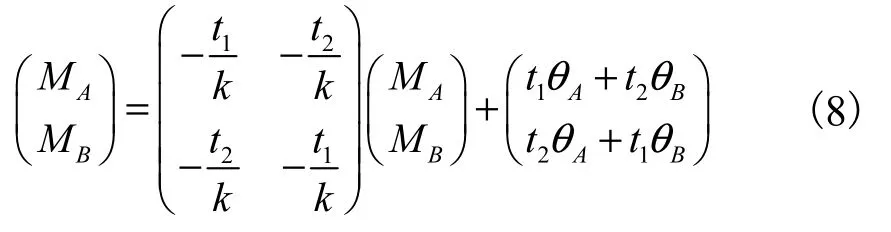
式中:t1=δ22;t2=-(δ22+δ12L).对式(8)进行计算,可以得到MA、MB的表达式为

两端由半刚性节点连接的预制混合梁梁端内力表达式为

1.3 局部坐标下的半刚节点预制混合梁刚度矩阵
在将上述梁单元端部力与梁端位移之间的关系写为矩阵形式时,需要将相关量统一方向,将其正方向按照矩阵位移法[13]中的规定,取A端为局部坐标系的原点,记作i,B端记作j,则有
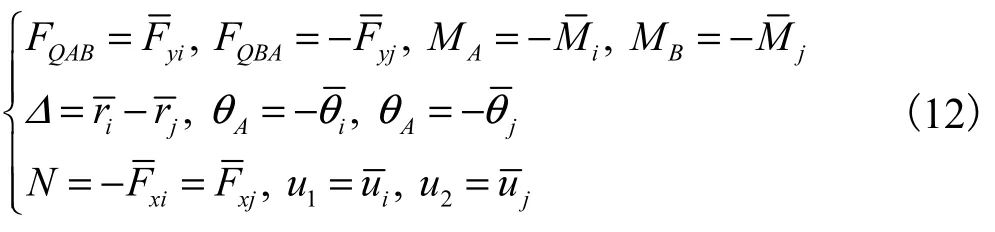
将关系式(12)引入式(11)并以矩阵形式表达,得到梁单元刚度方程为

式中:

半刚节点预制混合梁单元的刚度矩阵为

当k →∞时,式(15)可退化为梁端刚接时的刚度矩阵

若引入无量纲参数p、δ 满足

则式(14)可以改写为

式中,刚度系数p(0<p<1)反映了预制混合梁的半刚性特性,当p →0 时,结构连接趋于铰接,当p →1时,可认为结构为刚接.根据不等式

推导可知,无量纲参数δ介于-0.5~0 之间.
2 半刚性连接下预制混合梁框架抗侧刚度分析
为研究节点刚度对预制混合梁框架结构的影响,建立预制混合梁单层单跨框架结构简化计算模型,其跨长为L,结构层高为H.预制混合梁中混凝土梁与钢梁抗弯刚度分别为EcIc、EsIs,结构柱抗弯刚度为EI.预制框架在柱顶水平力F的作用下,预制框架结构顶部发生侧移量为1,计算模型如图3 所示.
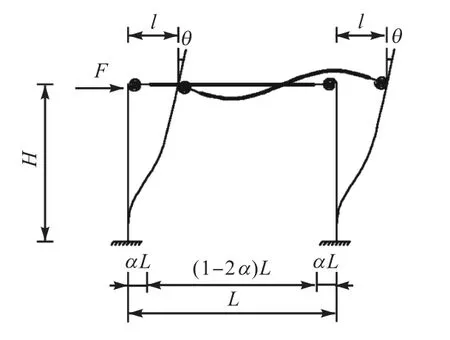
图3 带半刚性连接下预制混合梁结构计算模型Fig.3 Calculation model of precast hybrid beam with semi-rigid connections
显然,水平力F与半刚性连接下框架抗侧刚度P大小相同.忽略构件的轴向变形与剪切变形,利用考虑节点刚度的预制混合梁刚度矩阵求得解析解为
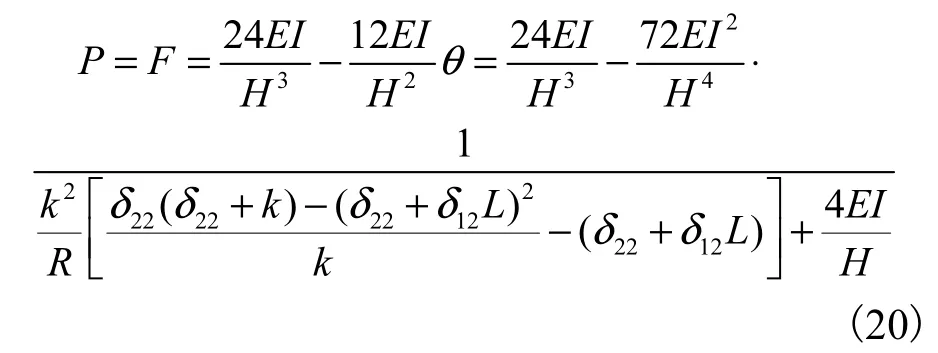
为研究半刚节点转动刚度对结构抗侧刚度的影响,通过改变转动弹簧的转动刚度k,结合预制混合梁长度比α,对结构的抗侧刚度进行分析.P0为刚接时的框架结构抗侧刚度,分析钢梁长度分别为0 m、0.2 m、0.4 m、0.6 m、0.8 m 时预制混合梁(预制混合梁与结构柱高度分别取为5 m 和3 m)的框架结构抗侧刚度与刚接时抗侧刚度之比P/P0.其中预制混合梁钢梁部分抗弯刚度取为1.6×107N·m2,混凝土主梁部分抗弯刚度取为5.1×107N·m2,结构柱抗弯刚度取为15.5×107N·m2,归一化结果如图4 所示.

图4 不同α 下半刚性预制混合梁框架的抗侧刚度Fig.4 Lateral stiffness of semi-rigid frame with precast hybrid beam corresponding to different α values
由图4 可以看出,转动弹簧刚度k在区间106~109.5(N·m)/rad 内框架结构的抗侧刚度随k的增大而逐渐增大,其半刚性特性对结构的抗侧刚度影响明显;当k小于106(N·m)/rad 时,结构抗侧刚度与铰接节点结构抗侧刚度接近;当k大于109(N·m)/rad时,框架节点可以近似看作刚接进行计算.同时,由图4 中还可以看出,框架抗侧刚度比P/P0关于刚度系数p的导数随α的增大而减小,且P0与节点刚度无关.从而可知随着α减小,刚度系数p的变化对结构抗侧刚度影响变大.
将预制混合梁及框架柱长度、混凝土主梁及框架柱抗弯刚度保持不变,预制混合梁长度比α取为0.1,e分别取为0.2、0.4、0.6、0.8、1.0,分析预制混合梁抗弯刚度比e在节点转动刚度变化时对预制混凝土梁框架抗侧刚度的影响,计算结果如图5 所示.由图可知,随着参数e的增大,节点转动刚度变化对结构抗侧刚度的影响增大.
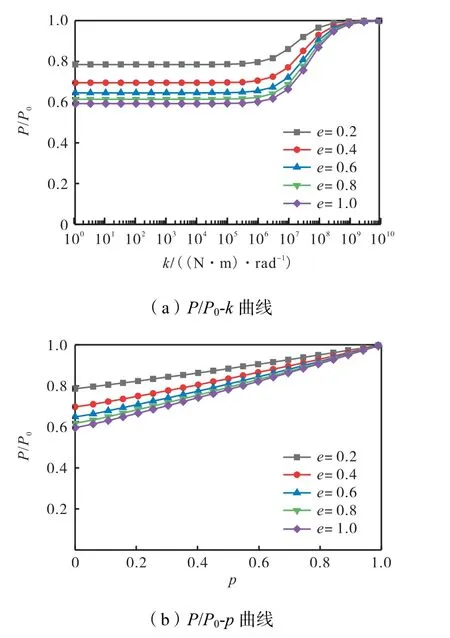
图5 不同e 下半刚性预制混合梁框架的抗侧刚度Fig.5 Lateral stiffness of semi-rigid frame with precast hybrid beam corresponding to different e values
另一方面,结构柱的线刚度i也将对半刚性节点预制混合梁结构的抗侧刚度产生影响.令预制混合梁及框架柱长度、混凝土主梁抗弯刚度保持不变,预制混合梁长度比α取为0.1,抗弯刚度比e取为0.3,结构柱的线刚度i取为参数δ22/L的1、2、3、4、5 倍,得到结构抗侧刚度与节点转动刚度之间的关系如图6所示.
由图6 可以看出,具有较小线刚度结构柱的框架结构,其对节点刚度变化更加“敏感”.同时通过图6(b)发现,随着结构柱线刚度不断增大,归一化后的结构抗侧刚度与刚度系数p逐渐接近线性关系.

图6 不同结构柱线刚度下半刚性预制混合梁框架抗侧刚度Fig.6 Lateral stiffness of semi-rigid frame with precast hybrid beam corresponding to linear rigidity of frame column
3 算例分析
为了验证本文结论的正确性并有效地对预制混合梁框架结构节点半刚性影响进行分析,拟对一个三层两跨框架结构进行计算,并利用二维杆系有限元模型进行对比.
3.1 算例结构形式
选取一个三层两跨预制混合梁框架结构,第1 跨长度为5 m,第2 跨长度为4 m,层高为3 m.其中两跨的预制混合梁钢梁长度与总长度比α均为0.1,钢梁采用H300×150×8×10 型钢,预制混合梁中混凝土梁部分截面为300 mm×400 mm,结构柱截面为500 mm×500 mm.在结构左侧梁柱节点处受水平荷载10 kN,结构节点的半刚性特性用转动弹簧代替,如图7 所示.
3.2 模型简化
本文研究范围为弹性阶段,需计算得出结构中各个构件的等效抗弯刚度.混凝土强度等级为C35,弹性模量依照文献[14]取为Ec=31.5 GPa,钢筋及钢材弹性模量取为Es=200 GPa.混凝土梁柱只考虑出现裂缝之前的弹性阶段受力情况,截面抗弯刚度可以视为常数,近似取为0.85EcI0[15],其中Ec为混凝土弹性模量,I0为换算截面惯性矩.

图7 结构计算模型Fig.7 Structural calculation model
如图8 所示,在考虑混凝土受压区作用的情况下,换算截面惯性矩

式中:h、b为截面高度、宽度;Ec、Es为混凝土、钢筋弹性模量;As为受拉区、受压区钢筋截面积;a为受压(受拉)钢筋至截面边缘的距离.
最终得到预制混合梁中混凝土梁换算截面惯性矩为1.848×10-3m4,H 型钢梁的截面惯性矩为7.77×10-5m4,结构柱换算截面惯性矩为5.596×10-3m4.
模型采用通用有限元分析软件ABAQUS 二维杆系结构模拟.结构各个构件均采用二维两节点梁单元(B21)进行模拟,截面特性及弹性模量均按实际设定,梁柱节点用多点约束(MPC)中的铰接(pin)并加入线性两结点弹簧(Spring2)进行连接,见图9.

图8 模型混凝土截面Fig.8 Cross section of concrete model

图9 有限元模型及计算结果Fig.9 Finite element model and calculation result
3.3 结果对比与分析
利用位移法及本文所推导的刚度矩阵可求出结构水平侧移量,图10 为理论层侧移量与有限元模型层侧移量对比.

图10 不同转动刚度下的侧移量Fig.10 Lateral displacements corresponding to different rotational stiffness
由图10 可以看出,刚度矩阵计算值与有限元模型结果吻合较好,推导得到的考虑半刚性节点预制混合梁刚度矩阵准确度较高.进而求得结构层侧移量与层间位移角随转动刚度k变化的趋势,见图11.
螺旋弹簧转动刚度小于106(N·m)/rad 时,结构受力情况接近于铰接,节点处几乎不传递弯矩,其结构侧移量相对较大.随着转动刚度的增大,结构中预制混合梁抗弯特性逐渐参与到结构整体受力.当螺旋弹簧转动刚度大于109(N·m)/rad 时,结构层侧移量几乎不再随节点转动刚度变化而变化.
随着转动刚度的变化,结构侧移量与层间位移角也在发生着较大变化.第1 层侧移量与层间位移角变化量受影响最小,转动刚度为106(N·m)/rad 时的侧移量与层间位移角分别是转动刚度为109(N·m)/rad 时的2.42 倍和2.43 倍.之后影响逐层增大,第2 层为2.95 倍和3.27 倍,第3 层为3.52倍和4.59 倍.
另一方面,转动刚度为106(N·m)/rad 时,第2、3 层的侧移量分别是第1 层的3.27 倍和5.99 倍,层间位移角分别是第1 层的2.27 倍和2.74 倍;随着转动刚度的增大,结构趋向于刚接,此时第2、3 层侧移量仅为第1 层的2.65 倍和4.02 倍,层间位移角此时为第1 层的1.65 倍和1.37 倍.这表明节点处转动刚度增大使得结构层与层之间侧移量与层间位移角的差距逐渐减小.将层间剪力与层间相对侧移的比值定义为层抗侧刚度[16],可以发现,随着节点转动刚度的增大,各层之间的层抗侧刚度逐渐增大,之间的差距随之减小.
综上可知,半刚性连接对预制混合梁框架的侧移量与侧移刚度的影响不容忽视.
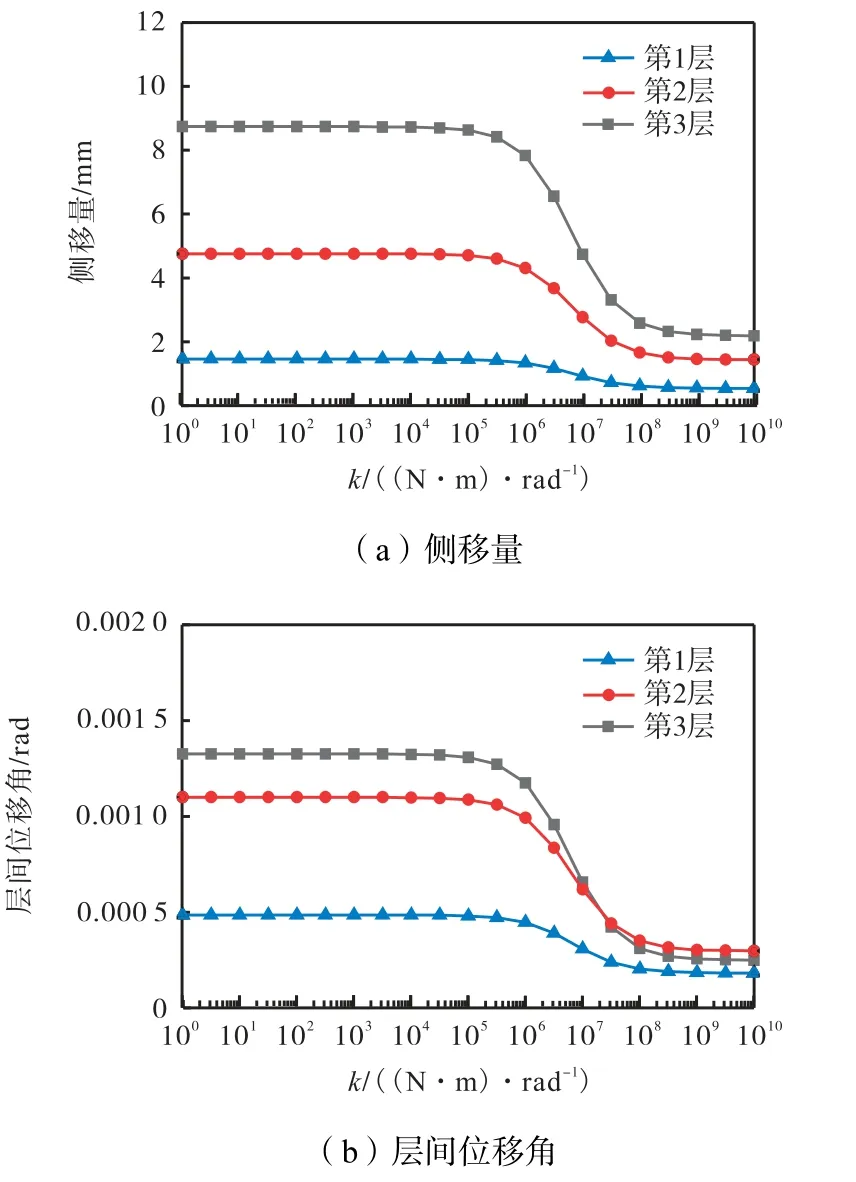
图11 结构侧移量与层间位移角的变化趋势Fig.11 Trend of lateral displacements and angle of floor displacements of frame
4 结 论
在预制混合梁两端刚接时端部反力与梁端位移关系的基础上,推导了预制混合梁单元考虑节点半刚性特性下的刚度矩阵,对预制混合梁框架结构抗侧刚度进行了分析,同时与有限元计算结果进行对比,得到如下结论.
(1) 具有半刚性节点的预制混合梁框架,其抗侧刚度随着节点转动刚度的增大而增大.介于0~1 之间的刚度系数p反映了预制混合梁框架的半刚性特性.当p→0时,结构连接趋于铰接;当p→1时,可认为结构为刚接.
(2) 转动刚度变化对结构抗侧刚度的影响程度与预制混合梁中长度比α、抗弯刚度比e及结构柱线刚度i的大小有关.随着α减小或e和结构柱线刚度i增大,节点转动刚度变化对结构抗侧刚度影响越大,结构抗侧刚度对节点的半刚性越敏感.
(3) 多层框架结构层侧移量的理论计算值与有限元模型吻合较好.随着转动刚度的增大,结构侧移量与层间位移角逐渐较小,层抗侧刚度增大,各层之间的侧移量、层间位移角与层抗侧刚度之间差距不断减小,且当弹簧转动刚度足够大时,半刚接结构侧移量逐步收敛于刚接时结构的侧移量.
