极射赤面投影坐标系二维间断有限元水动力模型

张庆河，王容基，李文俊，冉国全

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 中交第三航务工程勘察设计院有限公司，上海 200032)

随着计算机技术的发展，数值模拟方法在海洋动力环境的研究中得到了越来越广泛的应用．海洋动力如潮流等的模拟，一般通过有限差分法、有限元法和有限体积法等传统空间离散方法，求解浅水方程而实现．近年来，间断有限元(discontinuous Galerkin，DG)方法逐渐受到人们的关注．DG 的基本思想是在多项式空间内寻找近似解，不强制物理量在相邻单元的重合节点上相同，同时根据守恒性采用合适的数值通量实现相邻单元的耦合[1]．DG 方法兼具有限体积法和有限元法的优点，具有高阶精度和局部守恒性，适用多种自适应网格加密算法，同时还具有并行计算效率高的优势[2]．因此，利用间断有限元方法开发新型海洋动力数值模型，成为近年来海洋与海岸动力数值模拟的一个重要方向．目前DG 海洋动力数值模拟方面比较典型的工作有：Dawson 等[3]将DG 方法应用于大范围潮流和风暴潮模拟，源项和对流项采用标准的DG 格式，扩散项则采用降阶处理的局部DG 方法，通过求解球坐标系下的二维浅水方程，模拟了强飓风Ike 作用下的沿海潮波运动，计算结果表明该模型具有较高精度；Kubatko 等[4]建立了具有h-p 自适应的DG 浅水模型，求解沿海复杂水体运动，模拟结果和ADCIRC 有限元模型进行了对比，结果表明DG模拟结果更精确，并且在大规模计算时有更高的并行计算效率；Karna 等[5]在SLIM 间断有限元水动力模型基础上，提出一种全隐式干湿方法，保证了水深非负、质量守恒和数值稳定的性质，模型在数值实验和Scheldt 河口的实际应用中均得到验证．

除了上面提到的优点外，间断有限元方法也存在一定的缺点，如求解变量较多、计算量偏大等．为了减小计算量，李龙翔等[6]提出利用无积分节点间断有限元求解对流扩散方程，李文俊等[7]则进一步在直角坐标系下建立了无积分节点间断有限元二维浅水方程模型．

在研究大范围海域水流运动时，由于需考虑地球曲率和科氏加速度随纬度的变化，直角坐标下的二维浅水方程不再适用，通常需要求解球坐标下的二维浅水方程．普通经纬度球坐标系下的数值模型往往存在两方面的问题[8]：一是坐标奇异，模型中某些项趋于无穷大；二是经纬网格在极点附近网格辐合，通常有3 种解决方法，即改变格点划分并转换坐标系统[9-10]、引入滤波器[11]和采用隐式时间积分方法[12]，第一种方法是比较可行的，从网格划分上解决了网格辐合问题，通过转化到平面坐标避免了坐标奇异，间断有限元数值格式也容易实现．为此本文将采用极射赤面投影将球面坐标转换为平面坐标的方法求解球坐标下的控制方程，以建立可求解大范围海域水流运动的无积分间断有限元数值模型．

1 极射赤面投影坐标系二维间断有限元水动力模型的建立

1.1 极射赤面投影坐标系二维浅水方程

原始球坐标下的二维浅水方程为

式中：h 为总水深；t 为时间；η为相对静水面的波动水深；R 为地球平均半径；λ为经度，λ∈[0,2π)；φ为纬度；u、v 分别为λ、φ方向上水深平均速度分量；f 为科氏力分量，f=2ωsinφ，ω为地球自转角速度；K 为拖曳力系数，Cd为底摩阻系数；g 为重力加速度．动量方程(2)中右端第1 项为底坡源项，第2 项为科氏力项，第3 项为由径向和纬度方向相对运动产生的附加项，第4 项为底摩阻项．

本文采用的极射赤面投影法[13]如图1 所示，转换后的正交坐标x、y 和原经纬坐标系下的正交坐标λ、φ的映射关系为

式中m 为映射参数，通过几何相似得到，即图1 中NA′ 与OB 的比值，即

其中α为常量，对北半球投影变换时α=1 ，对南半球投影时α=−1．

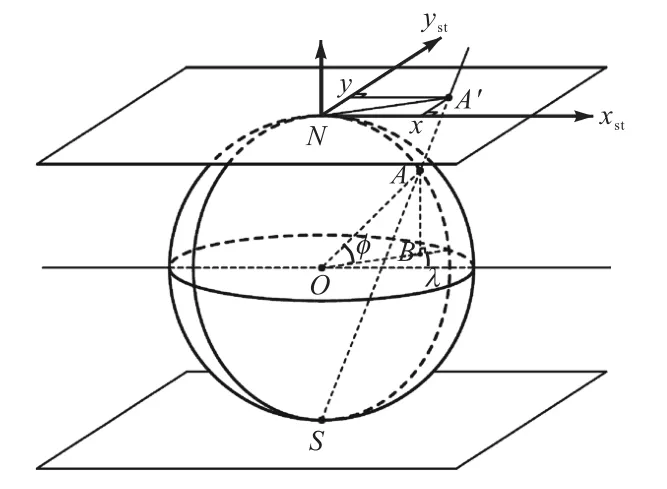
图1 极射赤面投影法示意Fig.1 Sketch of stereographic projection method

为保证数值模型的和谐性质，本模型采用Bollermann 等[14]的方法，对变换后的底坡源项进行改造，使底坡源项与压力项在静水条件下平衡，即采用式(5)对其进行拆分：

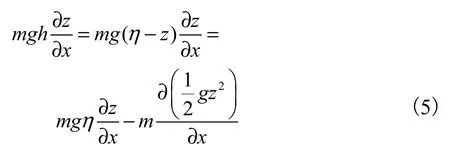
极射赤面投影坐标系下的速度场分量U 、V 与原经纬坐标系下的速度分量u、v 的关系为

最后，将式(6)代入经纬坐标下的底摩阻项，可得到极射赤面投影坐标下浅水方程的控制方程

其中，Cf为赤平投影坐标下的科氏力系数，

1.2 无积分节点间断有限元数值离散

采用节点间断有限元方法进行空间离散，令Ωk为求解域非重叠划分后的第k 个单元， Ω∂k为其边界，n 为边界处的单位外法向量．在定义计算域Ωk上最高不超过p 阶的多项式空间Vp(Ωk)上，选择基函数 φi( x )组成的线性组合作为近似解逼近U，其中为基函数系数，使得残差方程(8)达到最小．

在节点间断有限元方法中，插值基函数和试验函数均采用Lagrange 插值基函数定义，将近似解代入残差方程连续积分计算后，得到方程强形式，为

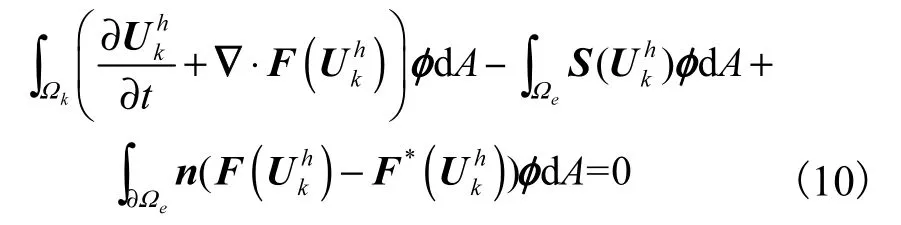
通量项的体积分和面积分计算均采用无积分方法[6]，利用节点基函数插值性质，将单元内通量项用基函数近似为

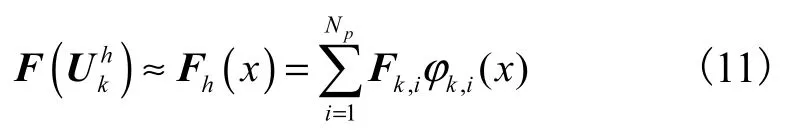
由于物理通量F 在边界是不连续的，有限体积法中成熟的数值通量方法可以容易地应用于间断有限元方法中，故引入法向通量数值通量F*[15]．进而可得到未知系数Uk关于时间的常微分方程

随后采用显式四阶五步龙格库塔方法时间递进求解，最终得到不同时刻具有高阶时间和空间精度的数值解．

1.3 边界条件处理

采用虚拟边界方法施加边界条件，在可滑移固壁边界中，水质点沿边界切向速度不变，法向流速为零，水位为零梯度，令分别代表虚拟边界节点和边界内部节点的物理量，虚拟边界物理量为

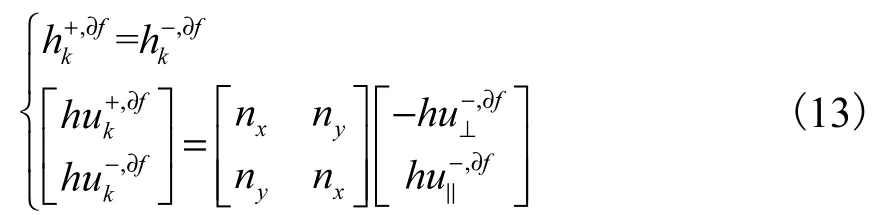
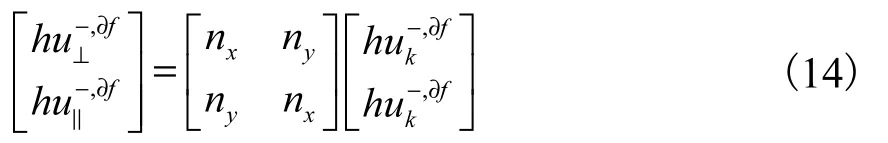
2 模型验证

为了验证本文建立的极射赤面投影坐标系下二维间断有限元数值模型的合理性，下面采用渤海海域两个不同尺度的算例对潮波和潮流运动进行模拟，并与实测数据进行比较．

2.1 渤海海域潮波模拟

2.1.1 模拟区域及计算配置

渤海潮波运动数值模拟区域包括整个渤海海域，其 模 拟 范 围 为：117.58° ～121.50°E ，37.14° ～40.91°N．图2 显示了渤海海域及模拟和实测潮汐分量进行比较的渤海验潮站分布情况．模型采用比三角形网格计算效率更高的非结构化任意四边形网格，利用有限元网格生成器Gmesh 生成，如图3 所示，整个计算区域共有5 974 个四边形单元和5 776 个网格节点，最大网格和最小网格尺度分别约为0.11°和0.02°，渤海水深数据源于 2005 年中国近海 1∶250 000 海图．模拟时东边界设为开边界，其他为陆地边界，开边界潮位从Chinatide[16]潮汐系统提取．模拟区域底摩阻系数统一取0.002，暂不考虑河流及风场强迫的影响．模型计算时间步长为10 s，模拟时间段为2006 年6 月29 日至2006 年8 月2 日，共35 d.

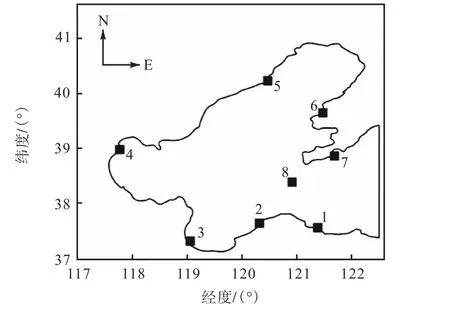
图2 渤海验潮站分布Fig.2 Tidal stations in the Bohai Sea

图3 渤海计算域水平非结构四边形网格投影图Fig.3 Distribution of the arbitrary quadrilateral meshes after being projected in the Bohai Sea

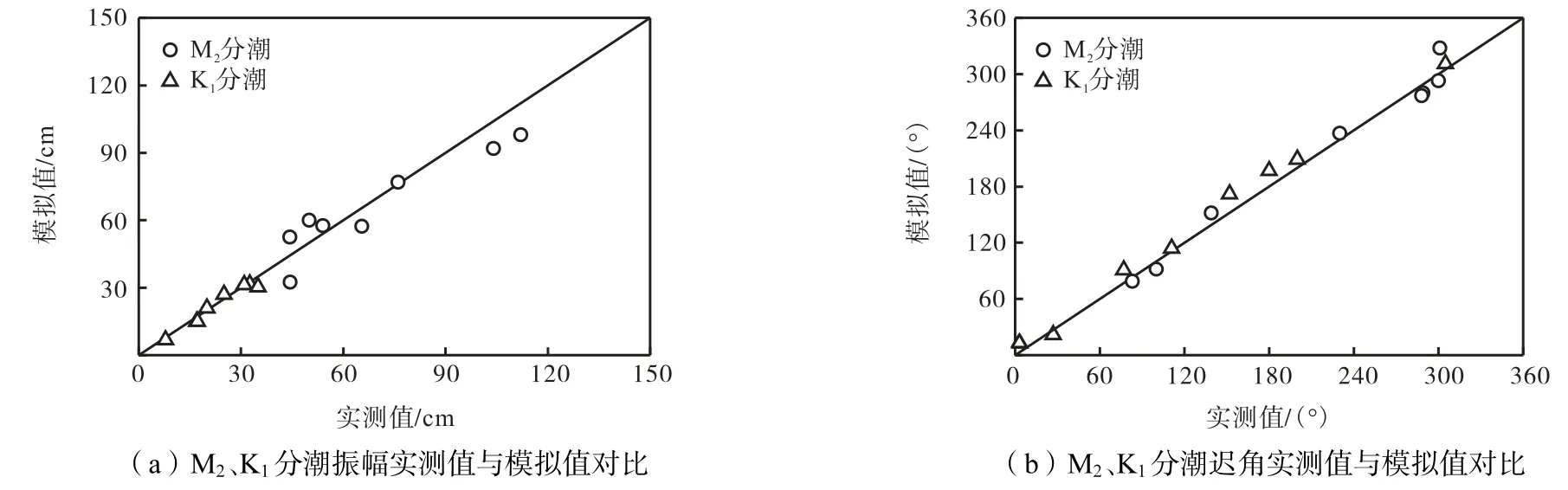
图4 M2、K1 分潮模拟结果检验Fig.4 Model validation of M2 and K1 constituents

表1 M2 和K1 分潮实测模拟调和常数比较Tab.1 Comparison between simulated and measured results of the tidal harmonic constants of M2 and K1

2.1.2 调和常数验证

根据准调和分析方法，采用T-Tide[17]对30 d 的潮位计算结果进行分析，得到计算区域8 个潮位站主要分潮M2和K1的调和常数，如表1 所示．图4 为M2和K1分潮8 个验证点模拟值与实测值的比较．模拟结果与渤海沿岸8 个验潮站M2分潮和K1分潮观测资料进行了对比，得到M2分潮振幅绝对平均偏差为8.60 cm，相关系数为0.938，迟角绝对平均偏差为10.75°，相关系数为0.990；K1分潮振幅绝对平均偏差为1.78 cm，相关系数为0.975，迟角绝对平均偏差为10.50°，相关系数为0.997．总的来看，不同测站M2和K1两个分潮的振幅和迟角与实测结果接近，模型对渤海潮波系统模拟结果较为准确．个别站点，如塘沽的振幅和迟角偏差较大，可能与近岸水深地形刻画不够细致有关．

图5 为M2和K1分潮的同潮图，模拟结果表明M2分潮在渤海海域分布2 个无潮点，分别位于黄河口附近(119°03′E，38°11′N)和秦皇岛外海(120°06′E，39°48′N)，K1分潮无潮点位于渤海海峡(120°42′E，38°16′N)，与沈育疆[18]、Fang[19]和朱学明等[20]研究中的无潮点位置接近．从等振幅线和等迟角线分布来看，本文模拟结果与已有研究成果都基本一致，能较好展现渤海潮波传播与分布特征．

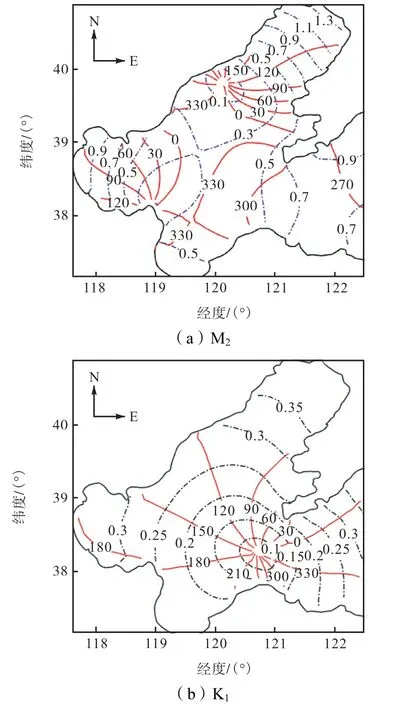
图5 M2、K1 分潮同潮图Fig.5 Cotidal chart of M2 and K1 constituents in the Bohai Sea

2.2 渤海湾局部区域潮流过程验证

2.2.1 模拟区域及计算配置

为模拟渤海湾东北部局部区域的潮流运动，对计算区域加密，整个计算区域共有19 436 个四边形单元和18 809 个网格节点，网格最大和最小分辨率分别约为0.05°和0.000 6°，相当于5 000 m 和60 m，如图6 所示．图7 显示拟进行模拟和实测水位、流速和流向的渤海验潮站分布情况，其中T1 为潮位测站，V1～V6 为潮流测站．区域地形数据取自1∶50 000海图(2011 年)，测站附近选用实测地形资料，模拟区域底摩阻系数统一取0.002，模型计算时间步长为0.8 s，模拟时间段为2012 年10 月8 日至2012 年10月20 日．

图6 渤海湾加密计算域水平网格投影分布Fig.6 Distribution of refined meshes after being projected in the Bohai Bay

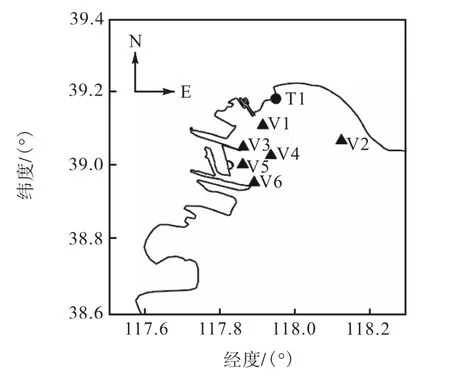
图7 潮流验证点空间分布图Fig.7 Observation stations for model verification in the Bohai Bay

2.2.2 潮位和流速、流向验证

图8 显示了2012 年10 月10 日至2012 年10 月20 日实测潮位过程和模拟潮位过程的比较情况．可以看出，T1 潮位过程验证点的模拟结果与实测水位过程比较吻合，相位基本一致，高潮和低潮位模拟都较好，模拟潮位最大误差为0.17 m．

图9 显示了2012 年10 月18 日至19 日大潮期间实测和模拟的流速、流向的比较情况．总体来看，各测点模拟流速、流向与实测结果吻合较好，部分时刻两者的差距可能和地形刻画不够完全准确以及底摩阻系数简单取为常数有关．

图8 T1验潮站潮位验证Fig.8 Tide level verification in station T1

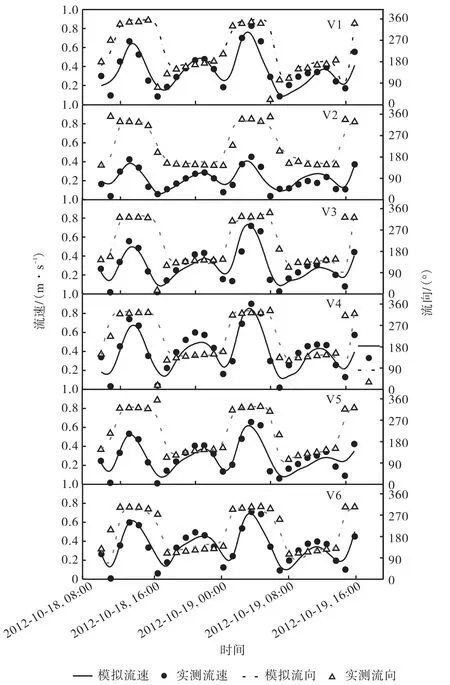
图9 V1～V6测站潮流验证Fig.9 Tidal current verification in stations V1—V6

总结上面两种不同区域尺度的模拟与实测结果的比较可以得知，采用极射赤面投影将球面坐标转换为平面坐标的方法建立的二维无积分间断有限元数值模型，可以较好地模拟大范围海域和局部海域的潮波传播和潮流运动．

3 结论与展望

为了利用间断有限元方法实现大范围海域的二维水动力模拟，采用极射赤面投影将球面坐标转换为平面坐标的方法求解球坐标下的浅水流动控制方程，建立了基于无积分节点间断有限元方法的二维水动力数值模型，并将建立的模型运用到整个渤海海域潮波和渤海湾局部潮流模拟．模型模拟结果与实测结果的比较表明，所建立的模型不仅可以较好地模拟大范围海域的潮波传播，而且通过非结构化四边形网格的局部加密，也可以较好地模拟复杂地形附近水位、流速和流向变化规律．今后我们将进一步加入波流耦合等功能，将该模型进一步推广应用于大范围海域风暴潮等问题的模拟．