基于材料韧性耗散的剩余寿命预测模型的对比分析及改进

高月华,冯艳龙,刘其鹏

(1.大连交通大学 机车车辆工程学院, 辽宁 大连 116028；2.大连交通大学 土木工程学院，辽宁 大连 116028;3.南昌航空大学 航空制造工程学院，江西 南昌，330063)*

交变载荷作用下，结构的主要失效形式为疲劳破坏，故而其疲劳寿命关系着整个结构的安全问题，诸多学者[1-3]为了准确的预测结构的疲劳寿命做了大量工作.

疲劳是指在交变载荷作用下,损伤不断累积，最终导致材料失效的一种力学行为[4].损伤作为描述疲劳演化的重要参量，由于不能直接测量，研究者通常根据材料疲劳强度[5]、剩余刚度[6]、韧性耗散[7]等定义损伤.叶笃毅等[4]通过大量的试验发现，在疲劳损伤过程中，结构的韧性变化最为明显.基于此，叶笃毅等根据损伤过程的能耗分析，提出了韧性耗散模型，也称为叶笃毅模型.近期，彭兆春[8]和王欣[9]又将此模型进行了改进，得到了预测精度更高的改进模型.

本文对韧性耗散模型及其相关修正模型在公式推导和剩余寿命预测方面进行了系统的对比和分析，结果表明应力比作为表征量时，无论是放在系数上还是指数上，均可以有效地反映载荷间相互作用的影响.对系数修正模型做了进一步改进，建立了新的简化模型，通过典型材料的试验数据对比，验证了模型在两级加载下的有效性.

1 韧性耗散模型及修正模型

通过对文献[1,8-9]的对比分析得出，无论是韧性耗散模型还是其修正模型均是由“用韧性表示的疲劳损伤演变律”导出

(1)

本文以二级加载中的高-低加载为例，对不同模型在公式推导方面进行深入对比分析.

如图1所示，σ1为第一级循环载荷；n1为σ1作用下的循环次数；σ2为第二级循环载荷；n2′为根据等效损伤原理，将第一级载荷σ1作用n1次的损伤等效为第二级载荷σ2作用下的损伤而得到的等效循环次数；n2为在第一级载荷σ1作用n1次后结构达到破坏时所经历的循环次数.疲劳累积损伤路径为O-A-B-P.

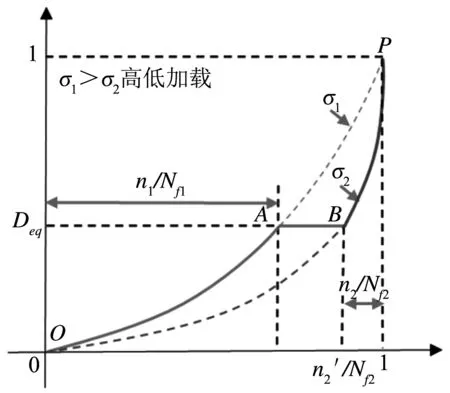
图1 二级载荷作用下的累积损伤

由式(1)知，当大小为σ1的应力作用于试件上并且循环次数为n1时，试件疲劳累积损伤值为：

(2)

当进行二级加载前，由于一级加载对试件已经造成了累积损伤，等效于以大小为σ2的应力循环n2′所造成的损伤：

(3)

1.1 叶笃毅模型公式

由损伤等效原理：

DA=DB

(4)

将式(2)与(3)代入式(4)中整理可得：

(5)

当σ2循环作用n2次后，构件发生疲劳破坏，此时累积损伤可表示为：

(6)

一般情况下，当累积损伤D达到临界值时材料会发生疲劳失效，而这个临界值在叶笃毅模型中取1，此时得到损伤判据为：

(7)

整理式(7)可得，二级加载时，叶笃义模型的剩余寿命的预测值为：

(8)

1.2 叶笃毅模型的修正

尽管叶笃毅模型形式简单、物理意义明确，但是在变幅载荷作用下，该模型这种传统的前后两级损伤等效方式并没有体现载荷间相互作用的影响，导致其寿命预测的精度并不理想.同时考虑到现有的非线性累积损伤理论中，很多模型，如Freudenthal-Heller模型[10]、Corten-Dolan模型[11]等，均是以应力比的形式来体现载荷间相互作用.基于此，彭兆春、王欣分别提出了各自的修正模型，文中分别称为指数修正模型和系数修正模型.下面以二级加载下的高-低加载为例，详细阐述损伤等效的过程，如图2所示.

图2 二级载荷作用下考虑载荷间相互作用的累积损伤

1.2.1 指数修正模型

为了研究载荷间相互作用效应对损伤累积的影响，彭兆春通过观察Marco-Starkey模型[12]和Manson模型[13]等发现，在损伤等效过程中，前一级加载与后一级加载的累积损伤之间存在着某种幂函数形式，基于此，对叶笃毅模型的损伤等效进行了改进，即：

DA=DBω1,2

(9)

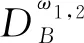
将式(1)与式(9)联立可得：

(10)

当σ2循环作用n2次后，构件发生疲劳破坏，对应的临界损伤值为1，得到损伤判据为：

(11)

整理式(11)可得，二级加载时，剩余寿命的预测公式

(12)

1.2.2 系数修正模型

为了考虑载荷相互作用效应的影响，王欣等[11]提出了另一种改进方式：

(13)

将式(2)与(3)代入式(13)中整理可得：

(14)

根据式(1)计算二级载荷作用下的总损伤

(15)

当总损伤度为1时，试件发生破坏，令式(15)中D=1可得二级加载时，系数修正模型的剩余寿命的预测公式：

(16)

对于上述韧性耗散模型及其修正模型的异同点总结如表1所示.

表1 三种寿命预测模型对比

1.3 寿命预测结果对比

本文以45#钢和2024Al的两级加载试验数据[14-15]为例，对比了叶笃毅模型、指数修正模型、系数修正模型的剩余寿命预测结果，如表2、图3所示.为了更加直观的体现各模型预测精度，引入相关系数这一参量，其计算公式如下:

(17)

其中,ρXY是X,Y的相关系数，cov(X,Y)是X,Y的协方差，EX,EY,DX,DY分别表示X,Y的期望和方差.

由于|ρXY|≤1，且越趋近于1表示两组数据越相关.所以从对比结果可以看出，指数修正模型、系数修正模型的剩余寿命预测值更趋近于试验值，预测精度优于叶笃毅模型.说明了在损伤等效过程中，应力比是一个有效的表征量，它作为考虑载荷间相互作用的影响因素的形式既可以是指数形式，也可以是系数形式.

表2 两种材料预测寿命与试验寿命相关系数计算结果

(a)45#钢

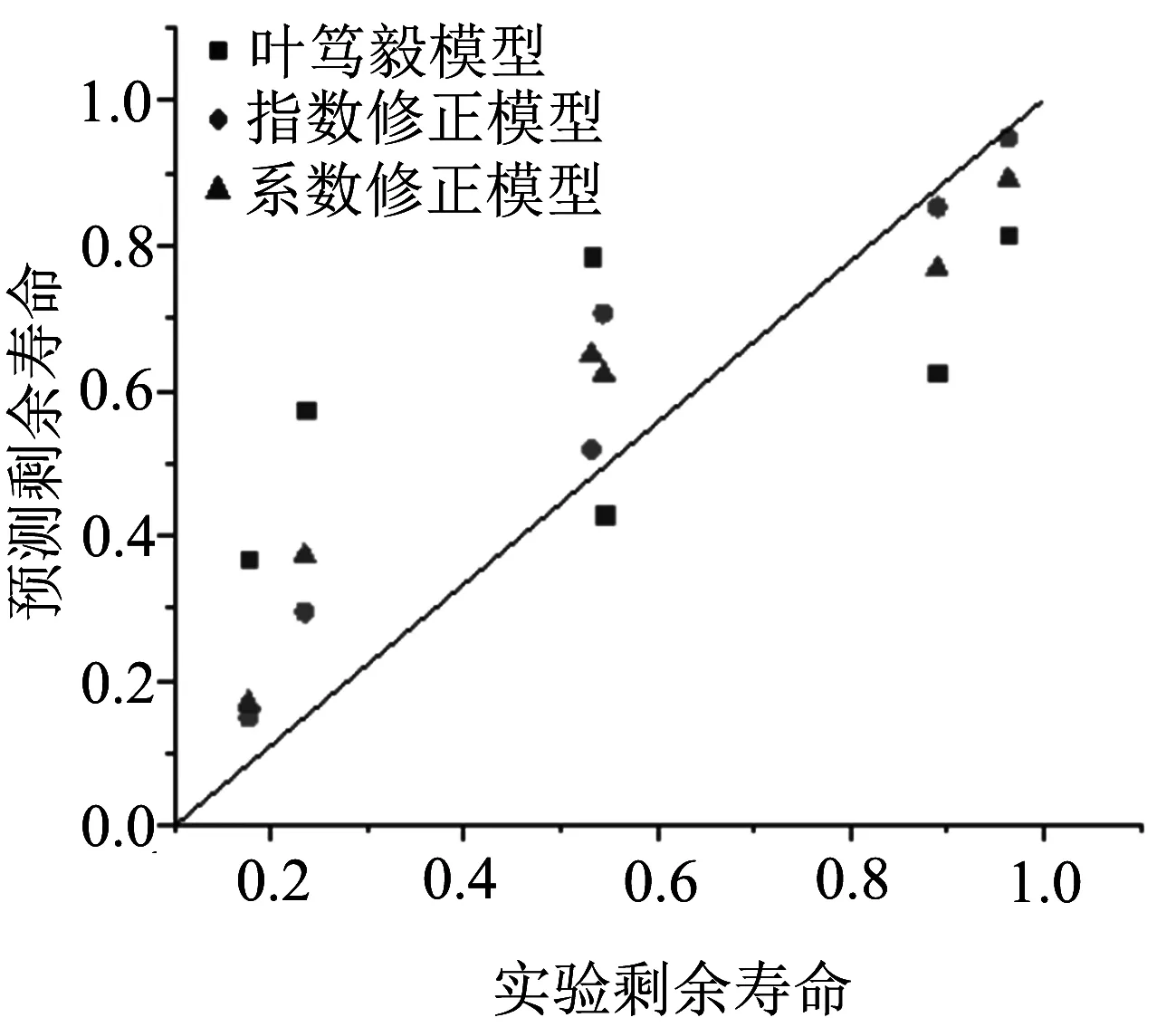
(b) 2024Al

2 系数修正模型的改进

2.1 公式推导的改进

令系数修正模型的累积损伤表达式为

(18)

当总损伤度为1时，试件发生破坏，令式(18)中D=1，可得二级加载时，系数修正模型的剩余寿命的预测公式为：

(19)

与式(16)相比，式(19)不仅推导合理，而且表达式更加简洁，更方便于工程实际的应用.

2.2 数据结果对比

为了验证改进后模型的合理性，仍以45#钢和2024Al的两级加载的试验数据为例，对比系数修正模型和本文提出的改进模型剩余寿命的预测结果，如图4所示.

从图4中的数据可以明显看出，系数修正模型与本文改进模型的预测剩余寿命结果几乎一致；从数学角度分析，1/Nf2是一个非常小的量，在公式中可以忽略不计.这均表明了本文改进模型的合理性与有效性.

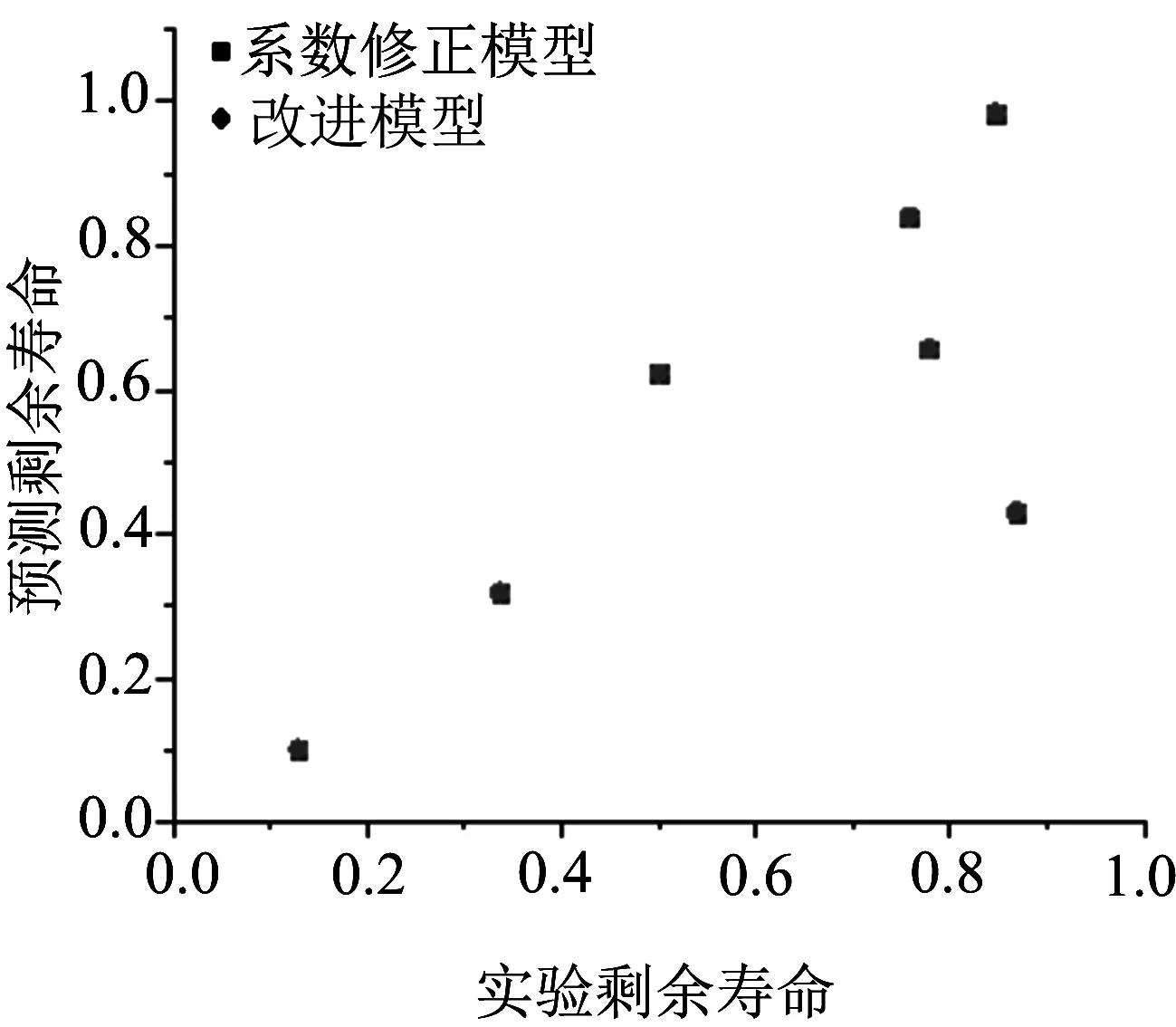
(a)45#钢

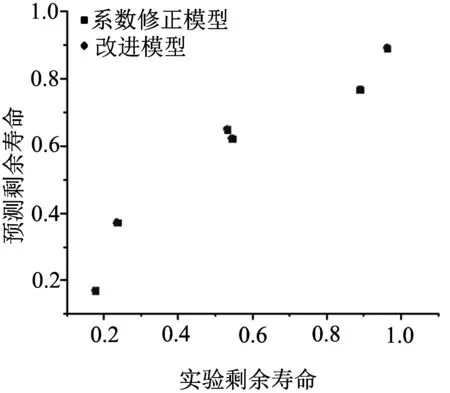
(b) 2024Al

3 结论

(1)在变幅载荷作用下，载荷的加载顺序和载荷的相互作用对疲劳累积损伤有很大影响.叶笃毅韧性耗散模型仅考虑了载荷加载顺序的影响，因此预测精度并不高.而指数修正模型和系数修正模型的提出对此进行了改进，使得预测精度得到了提高；

(2)对系数修正模型的损伤累积公式进行了进一步推导，得到了一个新的改进模型.所发展模型在保持预测精度不变的前提下，形式更为简洁，便于工程应用.