发展视角下优化思维的生长

“优化”是解决问题的一种最基本、最常用的思想方法。教师应基于发展的视角读懂教材、读懂学生、读懂课堂，为学生优化思维的生长引路，促进学生优化思想的形成。

一、研读教材脉络，把握知识体系

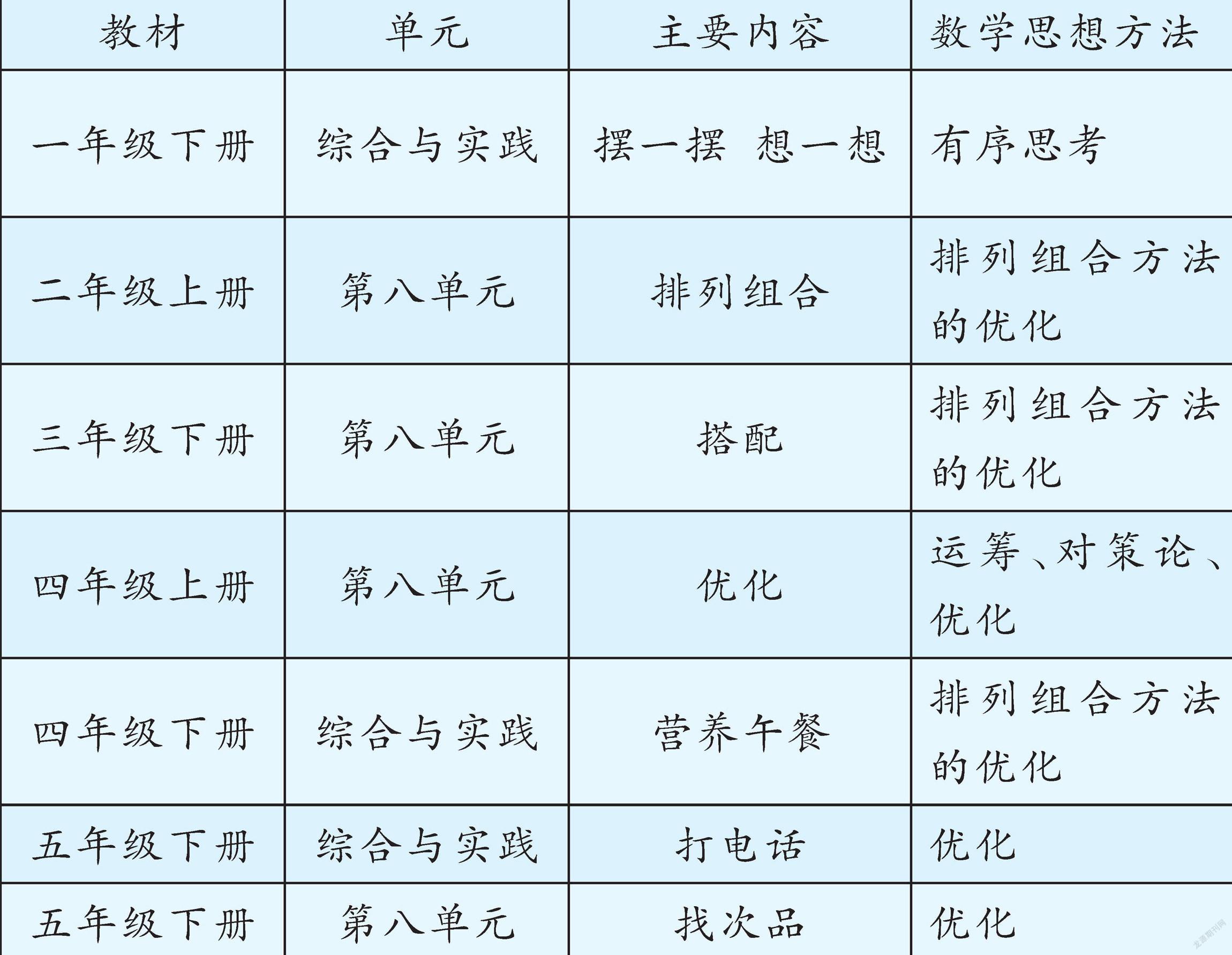
教材是学生学习的基本素材，研读教材尤其是纵向研读教材，有利于教师看到知识的全貌，找准知识的生长点和落脚点。有关优化的教学内容在人教版教材中大多以“数学广角”板块呈现，重在系统而有步骤地向学生渗透优化的数学思想方法，其内容编排呈散点状，在教材所要渗透的数学思想方法中占有较大比例。笔者对这部分内容进行了梳理（如下表）。

以上是优化问题中显性部分的内容，还有一些隐性部分的内容也不容忽视。如“租船问题”在人教版教材中一共出现三次。一是二年级下册教材第六单元，问题特点是只租一种船，理解的关键点是“最多”“至少”，思考方式是画图、符号与列式，解题方法一般归纳为“进一法”。二是三年级上册教材第三单元，问题特点是租车不止一种选择，理解的关键点在于可以同时用两种车，也可以只用一种车，思考方式是一一列举和列式，一般用列表法解决。三是四年级下册教材第一单元，问题特点是有两种船，租的方案有多种组合，理解的关键点在于租大船便宜，混合租比只租大船便宜，租的船上不空位更便宜，思考方式有假设、列举、比较、归纳，需要学生通过综合分析与运算来解决。

小学阶段优化思想方法的渗透是一个循序渐进的过程。一、二年级以感受、尝试为主，三、四年级以体验、明晰为主，五、六年级以理解、应用为主。尽管优化思想方法在教材中有不同的体现形式，但其最终目的是将复杂的问题简单化、条理化，将未知条件转化为已知条件，将看似无法解决的问题转化为可以解决的问题。教师在备课前要研读教材，厘清教材脉络，找出相似问题间的联系与区别，以发展的视角、整体的观念来设计教学。

二、紧扣思维起点，设计学习序列

优化策略多种多样，教师要结合不同的问题类型、已有信息和学生的思维水平，引导学生用一定的方法找出最合理的解决方案。这需要教师本身具有优化意识，能引导学生在分析问题、解决问题的过程中掌握优化方法，感悟优化策略。

1.整合信息

“优化”具有整合性，即将搜集到的信息有效地整合、迁移，从而优化解决问题的过程与结果。教材图文并茂，为学生提供了大量的情境，蕴含着很多有价值的信息，但也有一些干扰信息（无用信息或误导信息），需要学生根据条件和问题将它们筛选出来，排除干扰信息，再整合有用信息，最终找到解题思路。能否快速而精准地分辨出有用信息并进行整合，取决于优化方法的应用。

例如“沏茶问题”，教材主题图提供了很多的数学信息：①小明家来客人，需尽快泡好茶;②用时需最短，还需合理;③烧水需8分钟;④洗水壶需1分钟;⑤洗茶杯需2分钟;⑥接水需1分钟;⑦找茶叶需1分钟;⑧沏茶需1分钟;⑨要烧水需先洗水壶，再接水;⑩烧水的同时可以洗茶杯、找茶叶;？沏茶需要按照一定的顺序。教师通过问题串引导学生阅读并记录获取的数学信息，独立设计沏茶方案，如“沏茶的顺序是什么”“怎样安排节省时间”“哪些事情可以同时做”等。学生对信息进行取舍后，可以梳理出沏茶步骤：洗水壶（1分钟）→接水（1分钟）→烧水（8分钟）→找茶叶（1分钟）→洗茶杯（2分钟）→沏茶（1分钟），并指明“找茶叶”和“洗茶杯”可以交换顺序，也发现能够同时做的事情就同时做，可以节省时间，比如烧水需要8分钟，等待的时候可以去找茶叶、洗茶杯。在此基础上，学生对这些信息进行分析，制订沏茶方案，并从中找到合理且省时的最优方法。

教学中，教师要有意识地引导学生合理分析，并用简便的方法记录信息，用简洁而有条理的表达方式呈现分析问题的过程与结果，在各个教学环节渗透优化的思想方法。

2.对比分析

优化的前提是多样化，即在无限或者有限种方案、方法中甄别出最优的方案、方法。教师为学生提供自主探索的学习素材与合作交流的机会，能激活学生思维，让他们在实践操作与对比辨析中，体悟优化策略。

例如“烙饼问题”，教师在引导学生充分理解题意并独立思考后，组织学生分小组进行操作与讨论，边摆学具边说一说自己的方案，并将不同的方案展示在黑板上。随后，教师抓住“怎样省时”“怎么省时”“规律是什么”等关键问题，引导学生通过对比不同方案，体悟“最省时”的本质是“锅里每次都烙2张饼，不空锅”。学生经历了寻求最优策略的全过程，体验到优化思想的价值。

3.梳理总结

在教学优化问题时，教师应该给学生充足的时间与空间，让学生通过交流与反思获得顿悟，从而内化知识，在脑中形成清晰而稳定的优化策略，形成优化意识。

例如，总结“烙饼”最省时的方法时，教师首先引导学生发现“饼数是单数时，为了保证锅里总是有2张饼，一定要有3张饼交替烙”的思维关键点，得出最少烙饼次数就是饼的总面数除以每次可烙的面数，而最省时间就等于每面烙的时间乘最少烙饼次数，所以“最省时间=每面烙的时间×（饼的总面数÷每次可烙的面数）”。然后，教师提示：“这对所有的饼数都适用吗？”学生回答：“1张饼除外。”教师追问：“如果烙n张饼呢？”学生探索不同数量的饼的烙饼过程，列表记录相应的数量和时间，通过观察发现“排除只烙1张饼的情况，每增加1张饼，烙饼时间恰好多出3分钟”的规律。

又如，在總结全课时，如果教师只是单纯地问学生“这节课你学会了什么”，学生可能只会说出“我学会了烙饼”“我知道怎么烙饼省时”之类的话。其实，这节课上，教师采用多种教学手段让学生经历了从方法多样化到优化的全过程，学生的体验是充分的。为什么学生说不出来呢？笔者认为，这和教师的问题指向性有关。“学会了什么”指向知识的结果，而没有引导学生关注思维的过程，即优化过程。教师可以问学生“我们这节课是怎么研究烙饼问题的”，引导学生回顾学习过程，然后再提问“你有什么感受和收获”，使学生的思路逐渐清晰，思维更加严谨。学生只有亲身经历了优化的过程，才能在反思中顿悟优化策略，体会优化的价值。

三、瞄准思维“远点”，提升运用能力

优化思维与生活息息相关。教学时，教师要瞄准学生思维的“远点”，注重实际应用，促使学生在解决问题的过程中自觉运用优化的思想方法，促进自身思维与行为的条理化、简捷化。

教学中，在提炼出优化“烙饼问题”的根本是“每一次烙饼都用满锅的位置”之后，教师追问：“我们今天学习的烙饼问题，是不是仅能用来解决怎样烙饼最省时这一个问题呢？生活中还有哪些问题的解决可以用到这一方法？”学生在充分思考并回答后，教师播放视频，引导学生认识到寻求优化是人类的一种本能，大自然中也存在着这一现象，如蜜蜂的蜂窝结构巧妙、极度节省材料等。

优化思想是数学学习中的重要思想，不仅可以解决像“烙饼”“打电话”“找次品”等实际生活中的数学问题，还可以解决生活中经常遇到的求利润最大、用料最省、效率最高、费用最少、路线最短、容积最大等问题。如：快递员选择怎样的路线，能使路程尽可能短且安全？我们参加实践活动，怎样安排车辆最安全且花费最少？零食包装大小与价格之间的关系是怎样的？总之，优化问题无处不在。

（作者单位：孝感市实验小学）

余小莉，湖北省特级教师、湖北名师、湖北省名师工作室主持人，曾获得全国优秀数学实验教师、湖北省小数学科优秀教师、湖北省教学能手等荣誉，是孝感市“五一劳动奖章”获得者。工作室以“追求新理念，打造新课堂，践行新教育”为研修主题，以课题研究为抓手，关注常态课堂，努力发挥实验小学的辐射作用，力求将工作室打造成名师的摇篮。团队成员多次在省、市级优质课竞赛中获得一等奖，多篇论文在教学类期刊发表，多次承担课堂展示、送教下乡、区域研讨等各级各类教师培训与交流活动。