基于收益权重的均值-熵投资组合模型的研究
2021-01-07江璐瑶
江璐瑶,邓 雪
(华南理工大学 数学学院,广东 广州 510640)
0 引言
1952年,Markowitz的《Portfolio Selection》[1]一文的发表,标志着证券投资组合理论(也称投资分散理论)的产生,它主要是研究人们在预期收入受到多种不确定因素影响的情况下,如何进行分散化投资来规避投资中的系统性风险和非系统风险,实现投资收益的最大化。半个多世纪以来,人们在Markowitz研究的基础上不断进行深入探索,使得这一理论的发展日益趋于完善。证券投资组合理论主要有以下几家主流观点:Markowitz的“均值-方差”投资组合理论[1],Sharp的“资本资产定价”投资组合理论;Jansen的“非常规收益率”投资组合理论和Ross的“套利定价”投资组合理论等等。
随着学者们深入的研究,大量有关统计学的成果[2,3]被应用到投资组合研究中。其中,经典的均值-方差模型是采用组合收益的方差来度量投资组合的风险,用收益的均值表示投资者的期望效益,通过约束收益均值下极小化收益方差,或约束收益方差下极大化收益均值来选择最优投资组合,最终得到最优投资权重系数。但由于这种经典的均值-方差模型要依赖于收益率方差的存在,以及求解需要进行方差、协方差矩阵等复杂计算。因此,本文提出用均值-熵原理构建证券投资组合模型。同时为了构建的投资组合模型更加的贴合经济市场,我们还引入了无风险证券,其中Consigli[4]对含无风险证券的均值-方差投资组合模型也进行了一定的研究。
熵的度量在信息理论中起着极其重要的作用,是度量随机事件取值的不确定性程度,其应用范围也逐渐扩展到各个学科领域中。在信息论中,熵的测度是指对具有多个结果的离散随机变量取值的不确定性程度的度量,其中我们知道不确定性会随着熵值的增大而增大,同时掌握的信息也会增多,反之亦然。因此,熵作为一种新的风险度量工具开始广泛应用到金融等领域中,且通过与其他风险度量工具的比较,发现熵能够更加全面而准确的反映事件的不确定性信息。一方面,考虑到方差度量风险的局限性,曹静[5]基于熵的概念,在研究均值-方差模型的基础上,提出用最大熵原理建立证券投资组合模型;李华等[6]建立了几种关于熵的证券投资组合优化模型。随着对熵进一步的探讨,有关的学术成果也越来越多,诸如文献[7~9];Aksarayl[10]研究了一种基于均值-方差-偏度的多项式目标规划新方法,并提出了峰度熵模型。Jadhao[11]研究了熵在投资组合轮换策略中的应用。Brandtner[12]对最佳投资组合选择进行决策理论分析,特别是对比分析两种熵风险度量下的静态熵,相关熵风险度量(CERM)和C-均值凸熵风险度量(ERM)。Mehlawat[13]研究了基于均值-熵的多期投资组合模型。另一方面,在以往多数文献中,研究者往往假设收益率服从正态分布,用简单平均法计算的收益率均值衡量期望,但是在实际市场中,往往没有这么好的假设,导致用收益率均值衡量期望有一定的缺陷。李江涛等[14]提出用收益权重θt计算期望收益率,且基于熵的概念和国内市场的情况,建立了几种关于熵的证券投资组合优化模型。但是目前为止,缺少对这个模型合理性的验证和进一步的讨论比较,受以上文献启发,我们不仅引入θt和熵建立均值-熵模型,也通过实证分析讨论θt的合理性,熵方法和方差法的一致性,并通过与均值-方差模型作比较,进一步研究均值-熵模型。同时结合国内市场的情况,分别考虑了含无风险证券和不含无风险证券下的均值-熵投资组合问题。
1 基于收益权重的均值-熵模型
1.1 不含无风险证券的均值-熵模型
设有n种证券,且不含有无风险证券。其中令θt代表在第t个时间段的收益占T个时间段总收益的比重,rit记为第i种证券对应于第t个时间段的收益率记为第i种证券的期望收益率,xi记为第i种证券的投资比例,Rt记为投资第t个阶段的收益记为投资的总平均收益,pt记为第t个时间段证券收益的概率,那么的表达式为:

相应地,基于收益权重θt的均值-方差模型如(10):
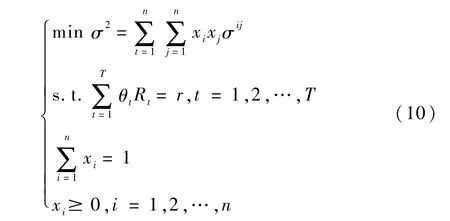
1.2 含无风险证券的均值-熵模型
在均值-熵模型(9)的基础上,引入1种无风险证券,记这种证券为第n+1种,且固定收益率为rf,相应的投资比例记为xn+1,则均值-熵模型如(11):

2 实证分析
2.1 数据的收集和处理
本文针对深证A股,考虑股票的规模、流动性、收益率等因素,从中选出5只股票作为研究样本,这5只股票分别为世纪华通(002602) 、同花顺(30033)、二三四五(002195) 、大富科技(300134) 、雷曼股份(300162) 。研究时限选取为2014年1月1日到2014年12月31日,收集的数据是这5只股票在研究时限内的月收益率,我们可以根据这5只股票的收盘价数据分析来推断收益率未来的收益趋势,其中股票的收益率定义为:rit=(pi,t-pi,t-1)/pi,t-1,其中Pi,t为第i种证券t时间的收盘价。
2.2 引入θt的合理性讨论
为了检验θt的合理性,我们建立均值-方差模型(10),其中利用收益权重θt来计算证券的收益率均值和相应的方差,通过赋予收益水平r不同的值,求出8种最优投资组合,其结果如表1。
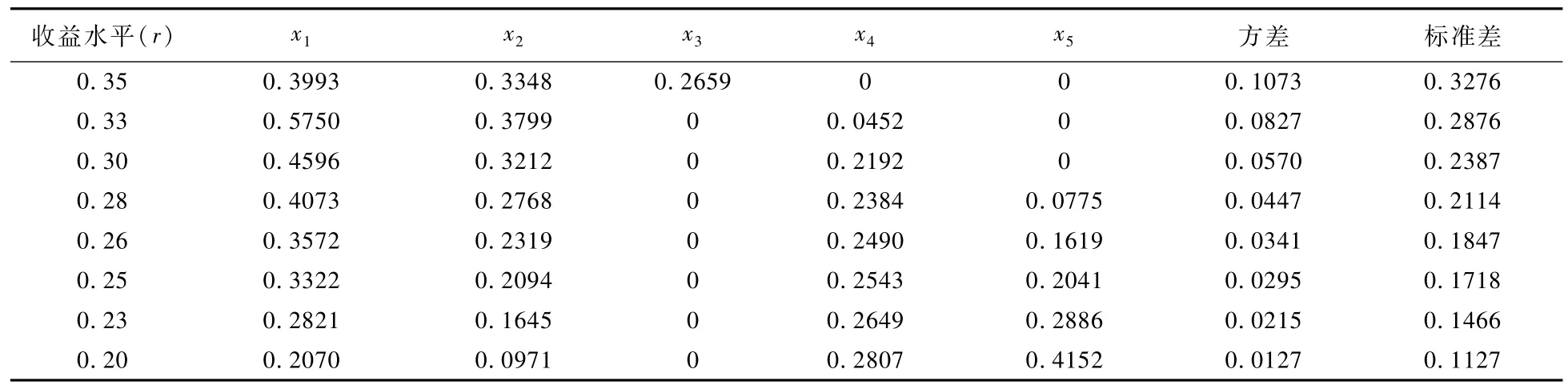
表1 均值-方差模型(10)的投资权重系数
根据表1,画出均值-方差模型(10)的有效边界,如图1所示:

图1 均值-方差模型(10)的有效边界
从图1中,我们可以看出随着收益水平的增加(减少),方差也随之相应的增加(减少),而且均值-方差模型(10)的有效边界图形的形状是一条较好的抛物线,这与经典的用简单平均法计算证券收益率均值时的有效边界的图形形状和走势完全一致,这说明引入θt计算证券的收益率均值具有合理性。
2.3 风险度量的熵方法和方差法的一致性比较
在均值-方差模型(10)中,我们得到了8种最优投资组合方案,以及每个收益水平所对应的方差。我们把表1中每种最优投资组合权重系数代入到均值-熵模型(9)中熵的计算公式中,得到如表2所示的数据:

表2 均值-熵模型(9)和均值-方差模型(10)方法的一致性比较
根据并在同一个图中做出熵和方差分别关于收益水平的变化趋势:
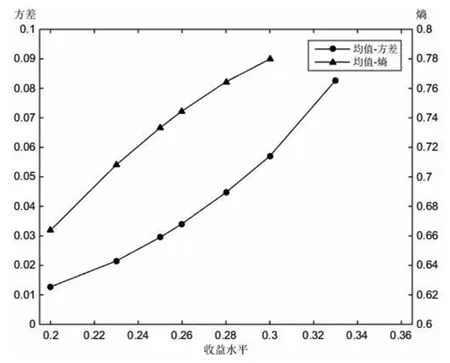
图2 均值-熵模型(9)和均值方差模型(10)方法的一致性比较
从图2中,我们可以看出熵的变化趋势和方差的变化趋势基本一致,随着收益水平的增加(减少),熵和方差也随之相应的增加(减少),而且均值-熵曲线和均值-方差曲线基本上是一种平行的关系,这说明在度量风险方面,熵方法和方差法具有一致性。但是均值-方差模型要依赖于收益率方差的存在,且收益率服从正态分布等假设条件,以及求解需要进行方差、协方差矩阵等复杂计算,而熵不受上述假设条件的约束,仅仅与收益率的分布概率有关,因此均值-熵模型在实际应用中能更好的刻画风险的特征。
2.4 基于收益权重的均值-熵投资组合问题
2.4.1 不含无风险证券的均值-熵投资组合问题
根据θt的定义,计算出θt的值,并把它代入到均值-熵模型(9)中。再利用Matlab软件,赋予收益水平r不同的值,求出相应的最优投资组合和熵值,其具体结果如表3。

表3 均值-熵模型(9)的收益和熵
2.4.2 含无风险证券的均值-熵投资组合问题
引入一种无风险证券,其月收益率rf为0.00385,把θt和0.00385代入到均值-熵模型(11)中。同样利用Matlab软件,改变收益水平r的值,求出相应的最优投资组合和熵值,其具体结果如表4。

表4 均值-熵模型(11)的收益和熵
根据表3和表4,我们可以发现在相等的收益水平r下,引入了无风险证券的均值-熵模型的熵值更小。
2.5 模型的分析比较
均值-方差模型是金融经济中广泛应用的一种模型,而均值-熵模型是以熵来度量风险,且熵不依赖于收益率的分布,仅仅与收益率分布的概率有关,从这方面来看熵度量风险更好。因此接下来我们从分散风险的能力来比较分析这两个模型,又因为考虑到要与均值-方差模型投资股票的种类保持一致,因此选择不含无风险证券的均值-熵模型和均值-方差模型,同时改变收益水平r,得到在不同的收益水平r下最优投资组合方案,两模型的比较结果如表5。

表5 均值-熵模型(9)和均值-方差模型(10)的投资组合权重比较
根据风险分散和投资组合原理以及对中国股票市场的调查研究得出的经验法则可知,组合对非系统风险有着一定的分散作用。从表5中,我们可以发现均值-熵模型的投资组合方案更加的分散,例如当收益水平r=0.26时,均值-熵模型的投资组合方案对5种股票的投资比例都大于零,其中股票002195的投资比例为0.2059,而均值-方差模型对股票002195的投资比例为0。因此在相同的收益水平r下,均值-熵模型能更好的分散非系统风险。
3 结论
随着市场经济的发展,投资组合越来越成为人们生活中一个热门的话题。投资组合通过分散化的投资来冲掉一部分的风险,因此深入投资组合理论的研究有利于投资者进行理智的投资。
本文通过对深圳A股进行筛选,从中选取5只股票进行实证分析。为了讨论θt的合理性,我们建立了均值-方差模型,发现均值-方差模型的有效边界仍符合同增同减性质,并且其图形是一条较好的抛物线,与用简单平均法计算收益率均值时的有效边界的图形形状和走势完全一致。我们还讨论了熵方法和方差法的一致性,发现在引入收益权重θt计算收益率均值时股票风险度量的熵方法和方差法具有一致性,但是由于均值-方差模型要依赖于收益率方差的存在,且收益率服从正态分布等假设条件,以及求解需要进行方差、协方差矩阵等复杂计算,因此从这个意义上讲,熵能够更好的刻画风险的特征。最后通过比较分析不含无风险证券的均值-熵模型和均值-方差模型,我们发现在相等收益水平r下,熵方法能够更好的分散投资风险。
