考虑灾后分区的应急物资LRP问题研究

郑 夏，马 良

（上海理工大学 管理学院，上海 200093）

0 引言

自然灾害是地球生活日常中的一部分，虽然科学技术在不断地发展，人类依然不能阻止或精确预测到自然灾害的偶然发生。过去的20年范围里，发生了许多海啸、洪水、地震、山体滑坡、火灾和一些其他的自然灾害。例如：一些重大型地震发生在1999年土耳其西北部城市伊兹米特、1999年台湾集集镇、2001年印度古吉拉特邦、2003年伊朗巴姆、2005年巴基斯坦克什米尔、2008年中国四川、2010年海地，共造成约45万人死亡；2004年印度尼西亚海啸、2005年美国卡特里娜飓风、2010年巴基斯坦洪灾，共造成30多万人伤亡和失踪，数十亿美元的资产损失，2000多万人无家可归。需要要解决的主要问题是：我们是否总是要遭受自然灾害的悲惨后果，或者是否可以用科学方法来防止伤亡和破坏？

近几十年来，如何在灾害应急管理中运用运筹学进行研究已经成为一个重要问题。应急供应链和应急物流管理中的优化函数和优化方法被用作分析工具和技术，为那些受灾地区的人们提供高效和有效的救济。因此，应急物资储备中心的选址分配问题即将成为一个世界性的引人注目的主题。基于人道主义的应急救援目的是向受灾点提供快速救援，最小化灾害对人们造成的伤害。正确的设计和运作应急物资供应链是实现有效和高效的应急反应的一个基本要素，尽管应急供应链可能和商业供应链有相似之处，但这两者针对服务对象的需求特征和决策目标则完全不同［1］。对人道主义救济链上的灾害作出反应的目的是向受影响地区迅速提供救济，以尽量减少人民的死亡和痛苦［2］。正确设计和操作救援链是实现有效和高效响应的关键要素；但直到最近几年，人道主义组织才注意到它的重要性［3］。在城市地区，地震会对入住率造成严重影响，迫使人们离开家园。因此，在灾害管理的准备规划阶段，市政当局应考虑为受灾人民提供紧急避难所和适当的应急设备和物资，从而减少人民的伤亡和痛苦，为幸存者带来救济。准备计划阶段的主要工作是为一个城市建立救援指挥中心、收集受灾地区的信息集合、确定合适的应急避难所位置、测定最佳疏散路线、运输车辆疏散和交付的材料、医学和防火站安装、应急设施建设［4］等。其中，以应急物资储备中心的位置选择和向受灾人民分配运输应急物资作为灾害应急管理准备计划中应处理的主要问题，两者也可综合称为选址路径（LRP）问题［5］，可以看作结合选址定位问题（LAP）和车辆路径问题（VRP）这两种相互联系的复杂非线性组合优化问题的一种混合型决策问题。关于应急或灾害管理模型的研究都是基于传统的覆盖问题的集合，具有一组需求点、约束和需求，应用数学建模技术，在地理区域中定位最优服务单元［6］。

目前，国外学者对设施选址问题（FLP）或选址-路径问题（LRP）进行了大量研究，如：Bozorgi-Amiri［7］等针对灾后人道主义救灾物流，在需求供给量和运输采购成本等作为不确定性参数的条件下，设计了一个多目标且稳定性较强的随机算法。Shariff［8］为了对马来西亚某区域的救助设备情况进行研究，提出了一个选址模型来求解其最大覆盖问题，并且设计了新型遗传算法进行模型求解。Murali［9］为了研究如何在危机发生后将药物等高效地分配给灾民，将某个发生较大型生化武器袭击的大城市作为背景，设计了一种考虑救援距离、被救援机率以及物资需求模糊等因素的药物储存点选址模型。Rawls［10］等以美国某地的飓风作为数据来源，对其所建立的为了解决突发性自然灾害下的应急设备的选址问题进行了验证和求解。Rawls［11］为了研究如何在灾害发生后的最短时间限制下进行灾民疏散，选择商场、图书馆等作为应急场所，构建了考虑需求模糊和非静态分配的模型。Dantrakul等［12］分别设计了改进的贪婪算法等三种优化方法来求解以运输花费最小化、建造成本最小化作为两个优化目标的应急设备选址模型。Erdemir等［13］使用贪心算法来求解综合考虑车运和空运方式的覆盖型应急设备选址问题。Jia等［14］为了解决洛杉矶某地区如何对自然灾害后的医疗物资储备点进行选址的问题，使用算例对所构建的选址模型进行了验证。Tzeng等［15］构建了考虑调度成本最小化和调度时间最短化两个因素的应急物资储备点选址-分配模型来完善灾后的物资调配体系。Nguyen等［16］建立了一种多级设施的选址-路径问题模型。Yu等［17］针对LRP问题模型，设计了模拟退火算法来实现优化。Yuan和Wang［18］使用蚂蚁算法求解应急调度问题中的调度线路模型。

国内学者针对FLP或LRP问题的研究如：曾敏刚等［19］构建了一种最小化总花费的减灾系统LRP模型，但是其使用两个阶段的优化方法对LRP问题中的LP问题和VRP问题分别进行了求解，丢失了求解集成化LRP的本意。代颖等［20］设计了一种混合遗传算法对所构建的模糊需求下考虑最大化救援满意度和最小化成本两个目标的LRP模型进行优化。郑斌等［21］设计了一种改进的遗传算法对所构建的模糊需求下考虑最短化调度时间和最小化调度成本两个目标的LRP模型进行求解。王绍仁等［22］设计了一种性能优于遗传算法的启发式算法来对灾后准备阶段针对单一物资、受灾点总需求量小于调度车辆总容量的选址-调度模型进行求解。王绍仁等［23］针对震后应急调度体系，建立了时间限制的模糊优化选址-路径模型。郑昊等［24］建立了考虑救援时间最早的连续型应急物资调配模型并给出了求解算法。

综上可知，LRP合并问题研究的文献不如LAP和VRP多，且大部分文献均是以物资运输时间最小、应急总成本最小、物资需求满意度最大当中的任意一种或两种为目标进行建模，求解模型的算法设计大多基于常见的几种优化算法如：遗传算法、贪婪算法、蚁群算法等。又由于应急物资储备中心选址合理性与物资运输时的车辆路径安排之间是相互影响的，因此，从系统整体优化的角度，将应急服务设施选址问题与物资运输问题结合起来，引入人文社会因素构建选址-路径问题模型，并设计较为新颖的算法来集成优化模型，将是整个应急供应链体系中一个重点研究趋势。

本文将研究考虑对受灾地分区后的应急物资储备中心选址与物资调配路径选择的集成问题，首先为灾后应急管理规划阶段构建了一种多目标应急物资储备中心选址-路径模型，该模型以人道主义受灾点人口覆盖最大、总成本最小以及受灾点应急物资未满足的总需求量最小为前提，基于Fibonacci迭代思想引入全局搜索能力较强的差分进化算法，设计了一种改进的差分进化生物地理学优化算法（IDEBBO）［25］，对模型进行优化求解，最后通过数值实验和算法对比，表明了新模型的合理性和实用性以及算法的高效性，可为灾后应急管理决策提供参考依据。

1 问题及数学模型

1.1 问题描述

自然灾害发生后，需要高效率地在灾区进行临时应急物资储备中心选址，并在有效的时间、运输量和物资量等约束下将应急物资从储备中心运输到需求点。这里，我们考虑将每个受灾地区和损害严重程度不同的区域使用划分区域和分区像素来表示。首先，可通过受灾区的相关准则（如以地震灾害为例，可以震源地作为受灾最严重地区）或检测工具统计损伤估计结果，将四种需求像素按四种颜色的排序为：红、黄、绿、蓝。其中：红色表示受灾害影响较严重的区域；蓝色表示整个较为安全的区域。分区的主要作用是可以确定各分区里物资储备中心的数量和位置以及这些中心对需求点的覆盖。由于这些像素是作为离散单元使用，因此在离散空间中考虑位置问题，每个像素的中心可表示其在模型中的坐标。图1所示为某受灾区根据其损害严重程度进行的10个子区域划分，其中红○表示受灾最严重的区域，只有一个。黄□表示受灾次严重区域，绿表示受灾较严重区域，蓝△表示较安全区域。

图1 受灾地灾害等级分区

图2所示为图1对应的应急物资配置图，图中应急救济链由左侧应急物资储备中心、中间四种不同的物资运输方式、右侧受灾地区灾害等级分区区域需求点组成。每个储备中心可通过不同的运输方式向其所在分区覆盖范围内的灾害需求点提供应急物资救援配置。

图2 应急物资配置图

综合图1和图2，所需决策的问题是：在灾害发生后的前期响应阶段，对受灾地区通过不同受灾程度进行受灾区域等级划分后，如何选择建立若干个应急物资储备中心，并在考虑应急物资储备中心容量、物资运输车辆容量和某运输通道对车辆的通容量限制下，同时满足储备中心的需求覆盖最大、应急物资救援总费用最小、受灾点应急物资未满足的总需求量最小这三个目标。

1.2 假设条件

为模型的普适性考虑，可作出基本假设条件如下：

1）灾后应急准备阶段，首先利用相关软件工具对受灾地区按最坏情况给予损伤估计。尽管救灾设备和应急物资的需求参数可能与实际情况存在差异，但可为规划阶段的灾害等级分区提供充足依据。

2）模型中考虑的救济分配项目包括食物和水、医疗和卫生包裹、原始救援工具、毛毯和布等，这些物品不需要任何特殊的存放设备。

3）有若干候选应急物资储备中心、应急物资需求点和不同类型的物资运输车辆。

4）根据受灾等级将整个城区划分为n个子区域（n≥4）。由图1可知，灾后地区受灾程度分为四个级别，因此按受灾等级划分的子区域最少为4个。

5）应急物资总需求量总是小于应急物资储备中心的总储备量，并且可以决定其所在分区供给范围内对其进行供应的储备点的总储备量。

1.3 符号说明

指数：g＝1，2，…，G（G≤4）—各受灾严重程度等级的，分别用红○、黄□、绿、蓝△由表示高到低四个级别的受灾程度；c＝1，2，…，C—灾后整个受灾城市根据受灾程度被划分的一定数量的分区；e＝1，2，…，E—应急物资储备中心应当存储的应急物资类型集合；m＝1，2，…，M（M≤4）—所有运输模式的集合，为方便研究，本文设置最多为四种运输模式；vm＝1，2，…，Vm—为每种运输方式m定义的车辆类型集合；a＝1，2，…，A—坐标（a，b）表示分区中b＝1，2，…，B—各结点的位置；v：为表示车辆可用性而定义的虚拟节点，且v∈（A，B）。

sc，（a，b），（a′，b′）—若应急设施储备中心点（a，b）允许服务需求点（a′，b′），则为1；否则为于0。换言之，每个储备中心都位于自己所在的分区覆盖范围内服务需求点。

sc，（a，b），（a′，b′）＝（a′，b′）∈c。

ac（a，b）—坐标（a，b）处作为应急物资储备中心的平均设置成本。

ad（a，b），（a′，b′）—坐标（a，b）与（a′，b′）的平均距离。

asce，（a，b）—坐标（a，b）处物资e短缺的平均损失成本。

we—物资e的单位重量。

acce（a，b）—坐标（a，b）处物资e的平均持有成本。

P（a，b）—坐标（a，b）处的人口。

DMe，g—受灾程度为g级时对e型物资的需求乘数。

MRe（a，b）—坐标（a，b）处对e型物资的需求。

MRe（a，b）＝

t（a，b），（a′，b′），m—运输方式m 下从储备中心点（a，b）到需求点（a′，b′）所需的时间。

de（a′，b′），t—e型物资在t时刻，需求点（a′，b′）处需求或供给的数量，供给为正，需求为负。

T— 物资需求点要求应急物资运达的最晚时间，即限制期。

LN—一个大数。

决策变量：COV（a，b）—若坐标（a，b）的总体人口被储备中心覆盖，则为1；否则为0。

RC（a，b）—若应急物资储备中心位于坐标（a，b）处，则为1；否则为0。

AMe，（a，b），（a′，b′）—e类型物资从储备中心点（a，b）运输到需求点（a′，b′）的数量。

SQe，（a，b）—e类型物资在储备中心坐标（a，b）处存储的数量。

MSe，（a，b）—储备中心点（a，b）处e类型物资的短缺。

Ze，（a，b），（a′，b′），m，t—运输方式m下在t时刻从中心点（a，b）运往需求点（a′，b′）的e类型物资数量。

TUDe，（a′，b′），t—t时刻需求点（a′，b′）处e类型物资未满足的总需求量。

1.4 模型建立

综合以上参数与决策变量，在满足应急物资储备中心容量、物资运输车辆容量以及给定限制期内要将应急物资运输到各需求点的条件下，可构建如下的灾后城市应急物资储备中心的多目标选址-路径优化模型-PCU：

其中，目标函数（1）为从人道主义救援的角度以最大的限度扩大受灾地区的总人口覆盖率，即对于任何一个灾害等级分区中的人口都将从应急物资储备中心获得物资救援；目标函数（2）分别由建立物资储备中心的总花费、物资在中心的总存储成本、物资在中心点短缺造成的总损失、物资由中心通过某车辆类型vm向需求点的总运输成本四个部分组成，旨在使应急物资救援过程中的成本（总花费）最小；目标函数（3）使某时刻某需求点处对于某种类型应急物资未被满足的总需求量最小：该目标函数首先从正面支撑目标函数（1）的人道主义思想，可逆向理解为某时刻某需求点对某类应急物资的满足量最大，其次可从侧面反映模型整体的时效性，即在某时刻之前的时间段内，某需求点处对于某类应急物资的需求均在最大时限范围内得到了最大供应，从而实现在某时刻点某需求点对某种应急物资的未被满足的总需求量最小；约束条件（4）使用传统最大覆盖约束以确保如果储备中心建立在点（a，b）∈c处，则可以覆盖所有需求点（a′，b′）∈c的人口需求，该约束与目标函数（1）一起构成了覆盖问题的主要结构；约束条件（5）为将应急物资从储备中心运输到需求点的必要条件，其最大物资转移量不能大于物资的存储量；约束条件（6）确保只有储备中心点才可以存储应急物资；约束条件（7）定义了每个储备中心的存储容量限制；约束条件（8）将短缺量定义为每个需求点的供需差；约束条件（9）为非线性约束，确保储备中心供给需求点的应急物资满足需求点的所有人口需求；约束条件（10）平衡需求点和储备点上的物资；约束条件（11）在储备中心点上强制物资平衡；约束条件（12）限制了物资运输道路上车辆类型的数量；约束条件（13）阻止了虚拟节点和其他节点间的物资流动；约束条件（14）确保物资运输必须满足车辆有足够的容量；约束条件（15）平衡了车辆在节点上的流动，车辆不必返回中心点，可在某次运输任务的最后一站等待，直到下一个调度命令到达；约束条件（16）通过车辆的累积可用性来限制路径中的车辆数量；约束条件（17）为连续非负变量；约束条件（18）为连续非负整型变量；约束条件（19）为二元变量。

1.5 模型转换

1.5.1 约束条件线性化

由于约束条件（9）是非线性的，增加了求解难度，这里通过引入一个新的整数变量的线性化技术将其转换为线性化形式，可使用式（20）～（25）来定义。

由此可将约束条件（9）替换为以下5个约束条件，重写为线性形式：

1.5.2 目标函数优先级化

由1.4节可知，该模型包含三个目标函数，我们采用对多目标函数进行优先级排序的方法使应急救援预算和应急物资覆盖区域的目标偏差最小。从考虑人道主义的应急救援角度可知，灾后应急管理规划的首要目标是最大程度对受灾害影响的人们提供物资救济，因此可假定目标函数F1为第一优先级。应急物资储备中心位置决策具有战略价值，需要大量投资，而目标函数F3中考虑物资运输属于战术决策且和其他物流成本有关，与目标函数F2中考虑设施设置等成本决策比较，优先级较低。故式（26）可作为模型PCU中新的目标函数：

式（27）～（29）作为三个新的约束条件加入模型PCU中。式（26）中ω1、ω2、ω3是三个目标函数的加权参数，且模型优先级为ω1≫ω2≫ω3，由于目标函数F1是一个最大化目标，因此在式（26）中考虑了与目标的负偏差，F2、F3均使用了正偏差。g1、g2、g3为三个可根据实际情况判断而定义的目标数量参数。

2 求解算法

由于模型PCU考虑了应急物资储备中心的选址及物资运输问题，属于NP-hard问题。为此，我们针对该模型提出一种新的基于Fibonnacci迭代的差分进化生物地理学优化算法（IDEBBO）：在原始 BBO 算法的核心思想上，首先考虑引入Fibonacci数列的迭代思想对种群内部的重复性个体进行有效消除，从而使种群精度得到提高，为了使IBBO算法中的变异算子得到改进，从而引入具有较强全局搜索能力的差分进化算法，最终得到一种改进的IDEBBO算法，通过对比FOA算法、DE算法、BBO算法，对模型-PCU的目标函数优化结果，表明所提IDEBBO算法在对函数进行优化时具有较强的跳出局部极值的寻优性能和收敛能力，可实现对于应急工程领域中涉及多目标及非线性等复杂问题的优化求解。

2.1 BBO算法原理

生物群体“栖息地”、适宜度指数（HSI，Habitat Suitability Index）随栖息地的变化而变化，栖息地的迁入率和迁出率用来描述其对栖息地中的群体迁移和分布的影响。栖息地适宜度的向量（SIV，Suitable Index Vector）是由与HSI有关的特征变量包括：物种多样性、地形多样性、气候多样性、植物多样性和降水量等因素构成的，其中，SIVs（Suitable Index Variables）是指具体的每一个适宜度变量。

2.1.1 迁移操作

BBO算法之所以能实现对全部解空间的搜索，是因为其栖息地之间的信息交互是通过迁移算子来实现的。HSI较高的栖息地物种较多，HSI较低的栖息地物种较少，因此，需要建立表征栖息地HSI与物种数量关系的映射函数。首先，栖息地根据其HSI高低进行从高到低排序，设栖息地数量为m，最大物种数为n，则栖息地i的物种数量：ki＝n-i，i＝1，2，…，m（i是各栖息地经过排序后的标号），令Hi表示向栖息地迁入，对应的迁入率为λi；Hj表示迁出栖息地，对应迁出的概率为μi，Hi（SIVw）表示栖息地的第w个SIV迁入。因此迁移过程、迁入率、迁出率可分别表示为：

其中，I表示迁入的最大概率，E表示迁出的最大概率，两者通常设值为1。

2.1.2 变异操作

由于栖息地的物种平衡态会被突发性自然灾害打破，栖息地的HSI值会因此随机事件被改变，BBO算法通过变异操作来模拟该变化。令Ps表示栖息地含有s个种群的概率，λs表示栖息地种群数量为s时的迁入率，μs表示栖息地种群数量为s时的迁出率，可根据Ps求出栖息地变异率，从而对栖息地的SIVs执行变异操作，来增加物种多样性。可用模型来构建时间t到t+Δt之间的变化过程，以下的三个状态会发生一个，由式（33）可得到该参数：

（1）在时间t有S个种群，且在时间t到t+Δt之间无种群再迁入或迁出。

（2）在时间t有S-1个种群，且在时间t到t+Δt之间只有一个种群的迁入。

（3）在时间t有S+1个种群，且在时间t到t+Δt之间只有一个种群的迁出。

令式（33）中的Δt→0，求极限可得：

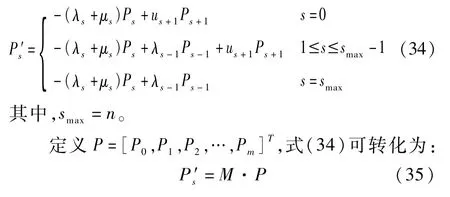
栖息地种群数目的概率可根据式（35）来求出。由于BBO算法中一个栖息地出现变异的概率大小与其种群数目的概率是一个反比的关系，则栖息地i的变异概率mi和物种数量的概率Ps关系如式（37）所示：

其中，mmax为最大突变值，Pmax为最大物种数量的概率。可知，HIS比较高和比较低的栖息地均具有比较高的突变率，而HSI居中的栖息地变异率很低。

2.2 IDEBBO算法设计

2.2.1 算法编码与初始化

将IDEBBO算法应用于求解应急物资储备中心的选址-路径问题，使用2.1.2节中的向量编码方式，每一组解向量对应于IDEBBO算法中一块栖息地的SIV，向量解对应的模型解（本文为目标函数Z的解）与IDEBBO算法中的HSI值呈反比，即一个向量经过解码后的Z越小，其对应的栖息地的HSI越高。此外，初始解采用随机方式产生。

2.2.2 对栖息地按照HSI值排序

对栖息地进行迁入、迁出、变异操作和精英保留操作之前，首先要对栖息地按照HSI的值由高到低进行降序排序。

2.2.3 精英保留

依次计算所有栖息地的迁入概率、迁出概率、突变率。IDEBBO算法在迭代过程会产生较优解，若直接进行迁移和突变操作可能会造成较优解的流失，使算法的寻优搜索能力减小，那么，可设计一个保留精英的策略，也就是每次进行迁移动作之前，对当前的两个最优解进行保留。

2.2.4 迁移操作

令N代表群体的大小，d代表维度的大小，rand代表0到1之间分布均匀的随机实数，如果rand＜λi，按照迁出概率用轮盘赌的方法选出一个栖息地迁出Hj，执行式（30）以更换Hi（SIVw）。

2.2.5 改进的消除重复性个体

Fibonacci数列的迭代思想中算法的时间复杂度和n成正相关，从（n＞2）开始执行，用变量的旧值递推新值，如F（n）＝F（n-1）+F（n-2），F（n-1）＝F（n-2），F（n-2）＝F（n），那么算法的时间复杂度为O（n），这是变量的新值不断地被旧值进行递推的过程，进而实现对于群体中重复性的SIV个体进行消除的目的，使算法的求解精度得到提高。也就是说，引进Fibonacci数列的迭代思想可对算法的时间复杂度以及空间复杂度起到很好的减小作用。

如果用s1表示全部迁入栖息地的SIVs根据HSI排序后的序列，用s2表示全部迁出栖息地的SIVs根据HSI排序后的序列.那么最后为了将群体中的重复性个体进行消除，需要判断isequal（s1，s2），若满足该判断，则迁出栖息地群体被重新赋值后可以表示为：

上式w1指第w1个栖息地中的SIV。算法的效率随着在循环过程里新值不断地被旧值递推出来而变高。对同样的群体个体，重新使用Fibonacci数列的迭代思想进行赋值，运行式（38）～（41），从而使重复的SIV个体被消除，使求解精度得到提高。

2.2.6 改进的差分变异算子

差分进化DE是一种具有较强稳定性的优化方法，未来的搜索是依据目前群体的范围和目标信息，其全局搜索能力由于其差分操作而比较强。所以，依据这个思想所改进BBO算法的变异算子为更高效的差分变异操作.执行式（42）更新Hi（SIVw）：

其中，Hx，Hy（x，y∈［1，n］且x≠y≠i）表示随机选择的两个栖息地.权重δ为0和1之间均匀分布的随机实数，Hbest是目前迭代里HSI最优的栖息地。依上式而知，变异操作栖息地Hi的SIV被其本身以及另外三个栖息地所影响。对Hbest与Hi和Hx与Hy进行差分操作，得出两个差分值，对差分值分别与权重系数δ相乘，将得到权重的两个差分值分别加到Hi（SIVw），那么，由于更过较为多样的信息可以被Hi（SIVw）接收，因此种群的多样性得到了增加。此外，Hbest是多样化信息中的构成部分，因而在搜索空间中，Hi更大概率地会向Hbest进行移动。

与BBO算法中原始的突变操作对比发现，全局搜索能力因改进后的差分变异操作而得到提高，同时可使突变操作在搜索空间内移向最优栖息地，一定程度上预防了较优迁移方案被破坏的情况。

2.2.7 IDEBBO算法流程图

如图3所示为IDEBBO算法流程图。

图3 IDEBBO算法流程图

2.2.8 算法的复杂度分析

假设栖息地规模为M，算法迭代次数为Tgen，需求点数目为N1，储备中心点数目为N2＝N（RC（a，b）＝1）：，车辆数目为，那么每个栖息地HSI值的时间复杂度为O（MN1N2Nvmlog N2），将每个栖息地的适宜度值进行排序的时间复杂度为O（M2），迁移算子时间复杂度为O（MN2），改进变异算子的时间复杂度为，改进的消除重复性个体的Fibonacci数列迭代思想中算法的时间复杂度为O（N2），因此，IDEBBO算法的时间复杂度为M（M+N2）+N2）），可以看出，算法的计算量主要与问题规模（需求点数量N1、储备中心点数量N2，车辆数量Nvm），算法设置的栖息地规模M 和迭代数目TGen相关。

2.3 IDEBBO算法伪码

表1 IDEBBO算法之差分变异操作

3 算例分析

假设某地发生自然灾害，救援部门首先通过对受灾地区按照相关灾害统计准则或检测工具统计损伤估计结果后，进行如图1所示的灾害等级分区，按受灾严重程度由高到低的分区数目依次为：1，3，3，3。假设有30个坐标点，其位置信息在5000km×5000km的平面坐标上随机生成，各坐标点之间的距离用平面坐标上的欧氏距离简化表示。由图2可知，物资储备中心只能服务其所在分区覆盖范围内的需求点，因此规定每个分区中必须选择建立一个物资储备中心点，那么可以在30个需求点中选择10个作为物资储备中心。可根据分区方式计算出参数应急物资类型、应急物资需求点、应急物资配送车辆等主要相关参数如表2～表4所示，由于篇幅限制，ac（a，b）等参数值不再一一罗列。

表2 应急物资参数

表3 应急物资需求点参数

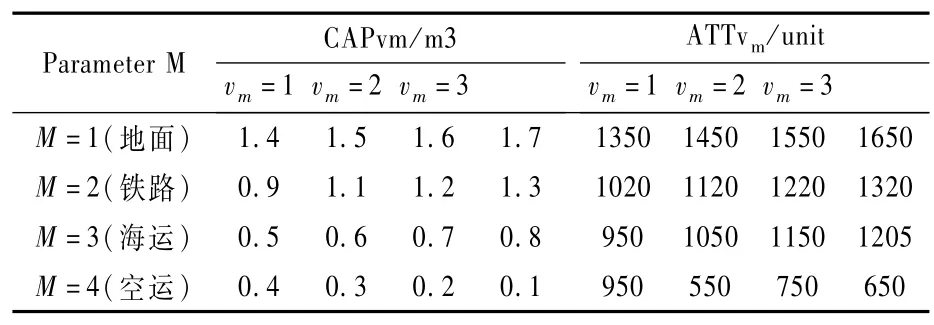
表4 应急物资配送车辆参数

3.1 计算结果

我们用Matlab 2016b编程实现前述IDEBBO算法，参数设置分别为：最大栖息地迁入概率I和最大栖息地迁出概率E分别设置为1，栖息地SIVs的最小迁入概率和最大迁入概率为0和1，最大迁移概率pmodify设为1，精英数目为3，最大突变率C＝0.2，差分因子δ为0.6，ω1＝0.5，ω2＝0.3，ω3＝0.2。图4所示为所得的选址方案，其中应急物资储备中心的位置序号按照受灾程度分区从高到低依次为：［9，（8，17，19），（21，23，6），（26，12，29）］。

图4 IDEBBO算法选址方案

表5所示为该选址方案下的车辆运输以及车辆类型安排情况。

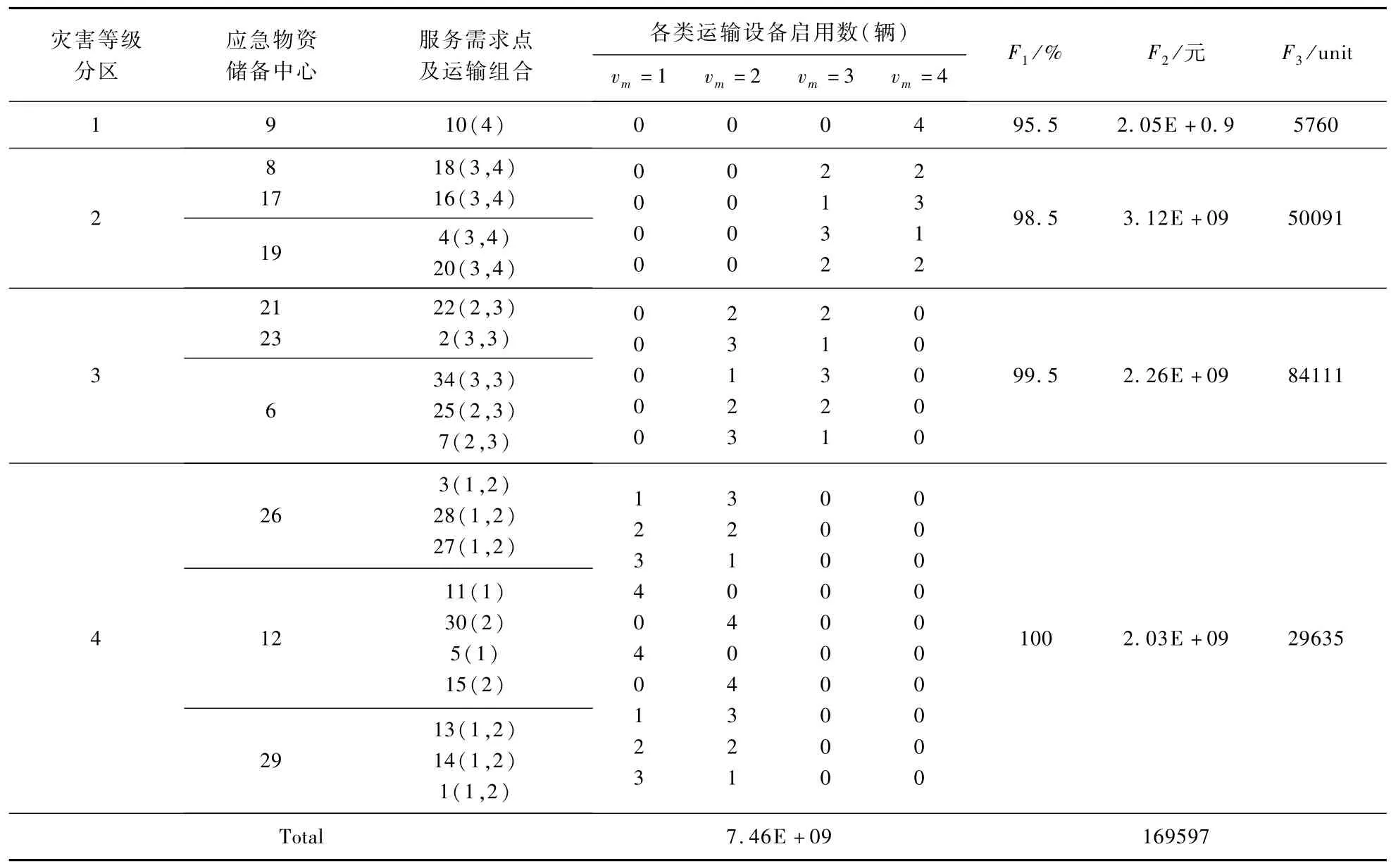
表5 运输方案

图6 目标函数F1 收敛情况

图5所示为该选址方案下车辆安排结果，其中用直线来简化表示节点之间的物资配送车辆路径，为直观显示，图中的实线来表示配送路线，虚线表示返回路线。运输车辆从储备中心出发后，首先前往最近的需求点，直到为所有该中心覆盖范围的需求点提供运输结束后才返回中心等待下一次任务。

3.2 算法分析

图6～图8所示为对比IDEBBO算法和BBO算法、DE算法、FOA算法时三个目标的迭代过程。

由图6可知，FOA算法所得覆盖率最小，DE算法由于全局搜索能力较强而稍优于BBO算法，本文所提的改进IDEBBO算法集成了Fibonnacci迭代思想消除重复性个体而提高求解精度的改进点以及DE变异算子的改进点提高了算法的全局搜索能力，使其能在较早的迭代中找到目标函数F1的最优值，即最大覆盖率，收敛性能优于其他三种算法。

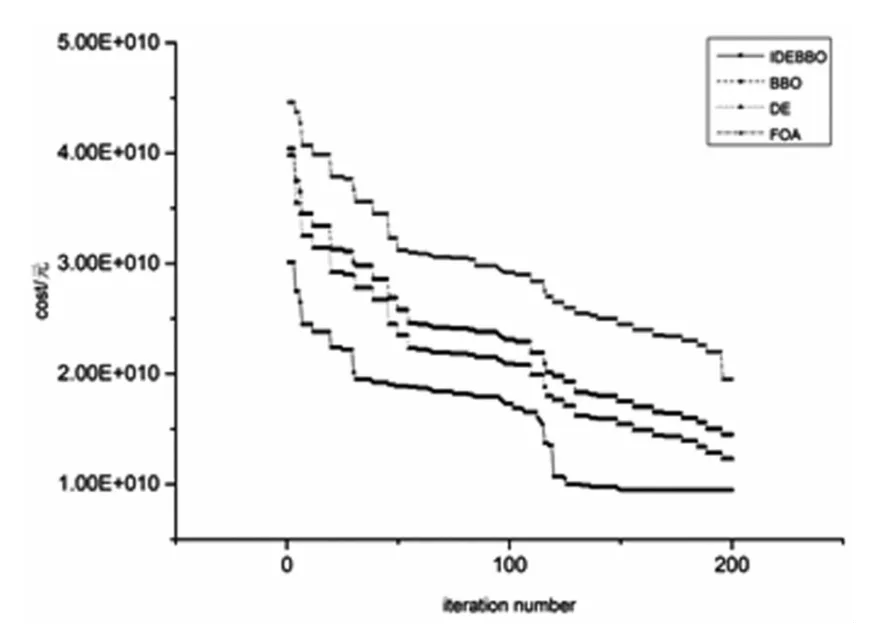
图7 目标函数F2 收敛情况

由图7、图8可知，IDEBBO算法在对目标函数F2，F3寻优过程中，同样在较早的迭代中寻得最优值，即分别为应急救援总花费最小和应急物资未被满足的总需求量最小。DE算法稍优于BBO算法，FOA算法寻优最差，IDEBBO算法整体最优。

图8 目标函数F3 收敛情况

表6所示为四种算法的计算结果比较。由结果可知，IDEBBO算法优化结果整体优于另外三种算法。

表6 四种算法结果比较

图9所示为四种算法各执行20次的算法效率对比，结果表明，IDEBBO算法因为引入考虑Fibonacci数列迭代的思想和考虑差分思想改进的变异算子，一定程度上影响了算法效率，但IDEBBO算法的寻优精度整体高于另外三种算法，遵循算法改进的中心思想，也就是保障算法效率没有被严重破坏的前提下，最大程度地增强算法的寻优精度。

图9 算法平均效率对比

4 结语

针对灾后前期应急管理规划阶段的应急物资储备中心选址-路径问题，本文首先构建了一种考虑灾后分区的多目标LRP模型，然后设计了一种改进的差分进化生物地理学优化算法（IDEBBO），该算法基于Fibonacci数列的迭代思想消除种群内部的重复性来提高种群精度，为了对IBBO算法中的变异算子实现改进，在消除重复性前提下，将具有较强全局搜索能力的差分进化算法中的差分思想进行引入，新的差分进化变异算子由此产生。最后通过数值仿真实验验证了所构建模型的合理性与必要性以及改进算法的可行性和有效性，可为实际应急管理决策提供参考，实现高效的灾后应急救援工作。由于改进算法集成了两个改进点提高算法求解精度，从而一定程度上影响了算法的运行效率，未来研究将集中在如何进一步提高IDEBBO算法效率，以及考虑灾后急救物资调配中的动态性等问题。