基于演化博弈的互联网信息服务业多元协同治理研究

卢安文，何洪阳

（重庆邮电大学 经济管理学院，重庆 400065）

0 引言

新时代背景下，网络强国建设无疑是我国迈进新时代的重要任务，而建立多元主体参与的协同治理模式是建设网络强国的有力保障。当前时期，为规避人口红利所带来的盈利风险，部分企业不顾政府及行业相关准则，大量采用违规行为获取利润，严重损害了用户合法权益，同时也不利于行业的健康发展。为了营造互联网信息服务业健康发展环境，我国政府不断优化中国互联网治理政策［1，2］。

近些年，考虑社会相关治理主体参与的多元协同治理模式逐渐受到学者们的关注，且已有部分学者对此模式在互联网行业的应用问题加以探讨［3，4］。许凤等基于贝叶斯网络方法，对互联网治理当中的参与主体协同度问题做了较为系统的实证研究，指出政府与网民协同度的提高对互联网治理具有积极作用［5］。Zajko，Mike对互联网行业治理过程中所涉及的参与者类型进行了研究，明晰了各参与主体的角色定位［6］。李雨峰、邓思迪对互联网平台的治理问题进行研究，指出政府规制与平台自治的多元治理模式能够发挥更好地治理效果［7］。叶大凤从利益相关者理论出发，建立政府和社会主体的决策机制与协调机制以应对政策冲突［8］。赵玉林提倡以政府统一引导，企业全面负责，社会广泛参与的多元治理模式实现协同共治［9］。褚松燕通过梳理、比较中国互联网治理的不同模式，指出多主体参与的治理模式具有较大优势［10］。通过对部分学者的研究进行梳理，可以看出在互联网行业的治理中，积极引入协会与公众是一种学术界基本认同的有效措施，同时也有部分学者注意到多元协同作用的有效发挥存在一定的条件限制，但当前研究缺少深入微观机理层面的多元协同治理模式研究，从而未能充分发挥协会与公众在治理过程中的主体优势。

在研究行业治理问题时，当前学者大都选取演化博弈的分析方法［11～14］。樊自甫、程娇娇、田苡毓运用演化博弈的方法研究社交网络平台上的有害信息治理问题［15］。卢安文、冯斐倩针对我国共享经济监管问题，通过建立三方博弈模型，探究有效维护行业健康发展的制度措施［16］。徐咏梅运用博弈理论研究中国企业的污染问题，指出对于企业排污问题，需要社会多方主体的共同参与［17］。张爽、孙绍荣、马慧民运用演化博弈研究了演化稳定策略，并进行仿真分析，探究政府垃圾收费政策在居民实施垃圾分类中的作用［18］。高宏玉针对我国水资源污染问题，通过构建博弈模型分析政府与企业之间的策略均衡，讨论相关影响［19］。从上述学者的研究我们可以看出，演化博弈方法能够较好地研究行业治理问题，对于讨论相关参数以及制度措施对治理效果的影响，提供了一种切实地研究方法，为本文采用演化博弈理论来研究互联网信息服务业的多元协同治理问题提供参考。

综上，为研究互联网信息服务业的多元协同治理问题，本文通过构建政府部门与互联网信息服务企业之间的演化博弈模型，探究协会与公众对于治理效果的影响，为今后政府部门更好地发挥多元协同治理模式的作用，营造良好的市场发展环境提供参考。

1 基础模型的构建、求解及分析

互联网信息服务业的多元协同治理涉及协会、公众多个参与主体，由于各主体在治理过程中的参与形式、作用效果的不同，其治理过程是一个复杂的系统问题，为了能够清晰的探究多元协同模式在互联网信息服务业中的作用效果问题，本文首先构建基础博弈模型，对协会与公众的参与问题进行讨论。在方便后续研究且不影响分析结果的基础上，将互联网信息服务业的多元协同治理模式抽象化为如图1所示的博弈关系框架。

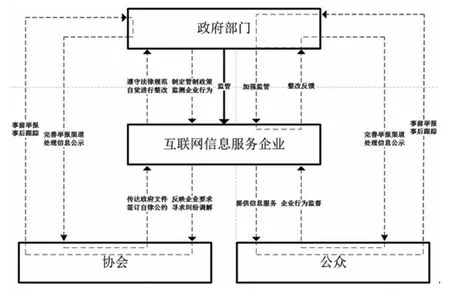
图1 各参与主体关系框架图

1.1 参数设定与模型构建

在互联网信息服务业的多元协同治理中，博弈模型主要涉及两个博弈方，一个是作为治理方的政府部门，另一个是作为被治理方的互联网信息服务企业，二者在治理过程中的策略选择集合分别为：S1（积极监管，放松监管）与S2（合规行为，违规行为）。并且，将协会参与治理过程的概率用参数p（0＜p＜1）表示，公众参与治理过程的概率用参数q（0＜q＜1）表示。由此，基本确定了互联网信息服务业多元协同治理的博弈模型。

1.1.1 参数设定与研究假设

为方便后文演化博弈模型的构建，对模型中所用到的参数进行说明，如表1所示。

表1 符号与说明

根据表1中的参数描述，结合互联网信息服务业多元协同治理过程中的实际情况，提出以下研究假设，帮助后文博弈模型的构建。

假设1政府部门在治理过程中，若选择积极监管的策略，则会获得相应收益S，即政府形象的改善以及社会效益的提升等；而若政府部门在治理过程中选择放松监管的策略，且公众发现企业采取违规行为并向政府部门举报，则政府部门存在损失n，即政府自身形象的下降等。

假设2政府部门在治理过程中若选择积极监管的策略，则需要付出相应的监管成本c，包括固定成本c0与边际成本两部分，而协会积极参与治理过程，可以帮助政府部门有效降低监管成本，协会对政府部门监管成本的作用可以用公式表示为：c＝c0+（1-p）／k。

假设3政府部门负责互联网信息服务企业的日常监管问题，而公众在发现自身权益受损，企业采取违规行为时，可以选择向相关政府部门举报，帮助政府部门对涉事互联网信息服务企业进行查处，公众参与对政府部门查处互联网信息服务企业违规行为的作用可以用公式表示为：μ＝λ+q（1-λ）。

假设4互联网信息服务企业在市场活动中，若积极采取合规行为，则可以获得收益d，并且合规行为的实施可以给社会带来收益m，政府部门也会给予企业奖励l；而若企业采取违规行为，则其可获得由于采取违规行为所带来的额外收益Δd，但却会使社会收益降低v。

假设5互联网信息服务企业若采取违规行为，会面临被政府部门查处的风险，若政府部门查处了企业，则企业需向政府部门支付z，同时还会遭受由此带来的潜在损失δ。

1.1.2 博弈模型的构建

根据互联网信息服务业多元协同治理的相关参数设定与研究假设，本文所构建博弈模型的收益支付矩阵如表2所示。

表2 博弈模型收益支付矩阵

其中：c＝c0+（1-p）／k，μ＝λ+q（1-λ）。

由表2可得，政府部门与互联网信息服务企业的复制动态方程为：

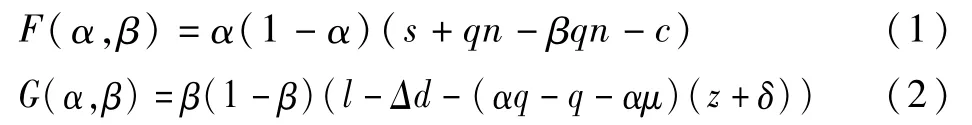
令dα／d t＝0，dβ／d t＝0，可得系统的5个局部均衡点，分别为（0，0），（0，1），（1，0），（1，1），（α*，β*）其中

1.2 博弈模型的求解与分析

1.2.1 模型求解

根据Friedman提出的方法，我们可以通过雅克比矩阵判断分析，得到本文所构建的互联网信息服务业多元协同治理博弈模型的5个局部均衡点a11，a12，a21，a22的取值情况，如表3所示。

表3 均衡点取值表

其中，A＝［l-（Δd-q（z+δ））］｛l-［Δd-μ（z+δ）］qn／［（q-μ）（z+δ）］2｝，B＝［（s-c）+qn］［q（z+δ）-μ（z+δ）］（s-c）／（qn）2，c＝c0+（1-p）／k，μ＝λ+q（1-λ）。

则该系统的演化稳定结果可以根据协会与公众的不同参与概率分为以下五种情况：

①当p＜p0且q＜q1时，系统的ESS为（0，0）；

②当p＞p0且q＜q0时，系统的ESS为（1，0）；

③当p＜p1且q＞q1时，系统的ESS为（0，1）；

④当p0＜p＜p1且q0＜q＜q1时，系统的ESS为（0，1）或（1，0）；

⑤当p＞p1且q＞q0时，系统的ESS为（1，1）。

其中：p0＝1-k（s-c0+qn），p1＝1-k（s-c0），q0＝

1.2.2 博弈稳定点分析

通过对博弈模型进行求解，我们发现协会参与概率p、公众参与概率q对于系统的稳定演化结果具有关键作用，二者的参与概率存在四个临界值，即前文所求出的p0，p1和q0，q1。同时，我们可以发现协会与公众的参与概率在临界值之间变换时，政府部门与互联网信息服务企业的均衡策略选择也会随之发生变化。通过对参数不同取值情况进行分析，我们可以清晰的认识到协会与公众在治理过程中的作用，具体结论如下所示：

结论1当p＜p0且q＜q1时，（0，0）点是多元协同治理博弈系统的稳定演化点。在此情形下，协会与公众参与治理的概率均较低，受到监管成本、手段等方面的限制，政府部门将采取放松监管作为自己的最优策略选择，而企业由于外部曝光风险较小，则会将采取违规行为作为自己的最优策略选择。显而易见，协会与公众的参与概率在此范围时，互联网信息服务业难以实现健康发展。

为了清晰地展示该情形下，政府部门与互联网信息服务业策略选择的演化均衡过程，笔者选择采用Matlab软件进行仿真模拟，令p＝0.3，q＝0.3（其余非分析参数此处不列，下同），代入程序运行得到如图2所示的系统仿真图像。

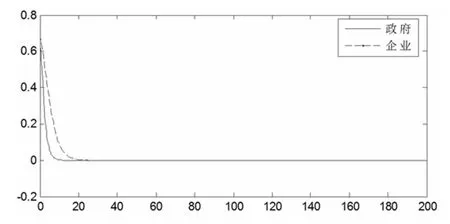
图2 （0，0）点的系统仿真图

从图2中我们可以看出，在此情形下政府部门与互联网信息服务企业的策略选择朝着（0，0）点演化，软件仿真图形符合模型求解结果。

结论2当p＞p0且q＜q0时，（1，0）点是多元协同治理博弈系统的稳定演化点。在此情形下，协会积极参与治理过程，使得政府部门的监管成本所有降低，因此政府部门将选择积极监管策略，而此时公众在治理过程中的参与概率仍处于较低水平，企业被曝光的风险较小，因此企业采取违规行为。

为了清晰地展示该情形下，政府部门与互联网信息服务业策略选择的演化均衡过程，笔者选择采用Matlab软件进行仿真模拟，令p＝0.7，q＝0.3，代入程序运行得到如图3所示的系统仿真图像。

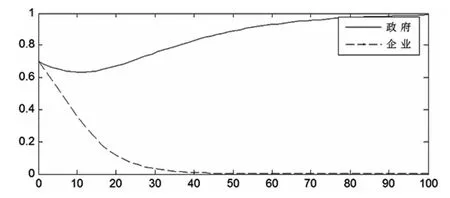
图3 （1，0）点的系统仿真图

从图3中我们可以看出，在此情形下政府部门与互联网信息服务企业的策略选择朝着（1，0）点演化，软件仿真图形符合模型求解结果。

结论3当p＜p1且q＜q1时，（0，1）点是多元协同治理博弈系统的稳定演化点。在此情形下，协会未积极参与治理过程，政府部门若选择积极监管策略，其仍须付出较高的监管成本，因此政府部门将采取放松监管作为自己的最优策略选择，而公众参与治理的概率有明显提高，企业若采取违规行为极易被曝光，因此其将采取合规行为作为自己的最优策略选择。但由于此种情形极度依赖公众的参与，在现实情境中难以出现。

为了清晰地展示该情形下，政府部门与互联网信息服务业策略选择的演化均衡过程，笔者选择采用Matlab软件进行仿真模拟，令p＝0.5，q＝0.8，代入程序运行得到如图4所示的系统仿真图像。

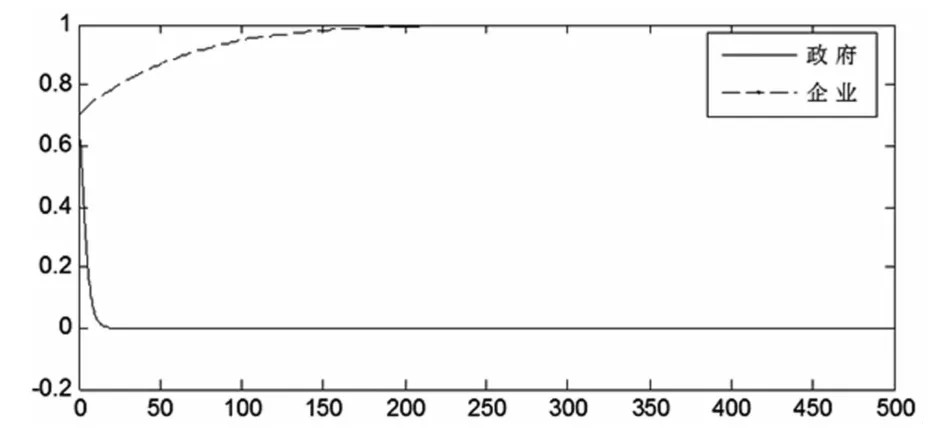
图4 （0，1）点的系统仿真图

从图4中我们可以看出，在此情形下政府部门与互联网信息服务企业的策略选择朝着（0，1）点演化，软件仿真图形符合模型求解结果。

结论4当p0＜p＜p1且q0＜q＜q1时，系统无稳定演化方向。系统的演化结果呈现出一种周期性变化。

为了清晰地展示该情形下，政府部门与互联网信息服务业策略选择的演化均衡过程，笔者选择采用Matlab软件进行仿真模拟，令p＝0.7，q＝0.72，代入程序运行得到如图5所示的系统仿真图像。

从图5中我们可以看出，在此情形下政府部门与互联网信息服务企业的策略选择呈现一种周期性的变化，没有一个稳定的演化趋势，软件仿真图形符合模型求解结果。

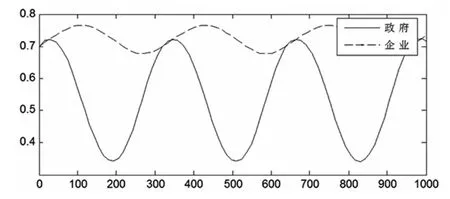
图5 混沌状态的系统仿真图

结论5当p＞p1且q＞q0时，（1，1）点是多元协同治理博弈系统的稳定演化点。在此情形下，由于协会与公众均积极地参与治理过程，政府部门的监管成本得到大幅度的降低，因此政府部门将采取积极监管作为自己的最优策略选择，而企业则面临着违规行为被曝光的外在风险，因此企业将采取合规行为作为自己的最优策略选择。此种参数取值范围对于实现互联网信息服务业的健康发展具有积极作用。

为了清晰地展示该情形下，政府部门与互联网信息服务业策略选择的演化均衡过程，笔者选择采用Matlab软件进行仿真模拟，令p＝0.7，q＝0.72，代入程序运行得到如图6所示的系统仿真图像。

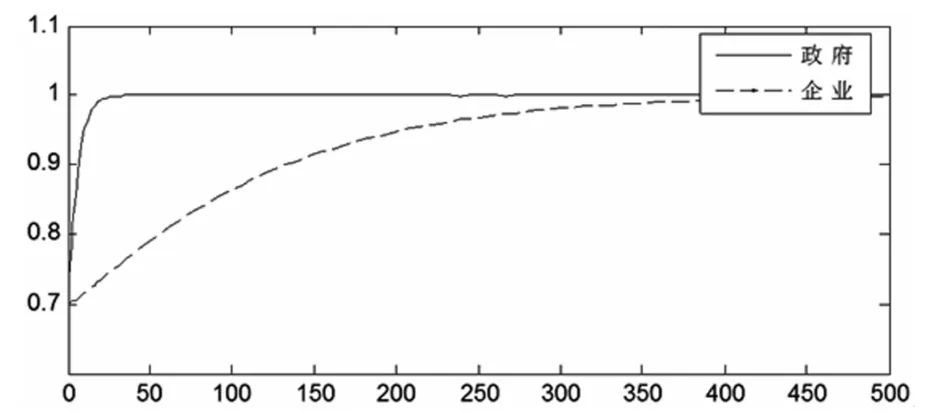
图6 （1，1）点的系统仿真图

从图6中我们可以看出，在此情形下政府部门与互联网信息服务企业的策略选择朝着（1，1）点演化，软件仿真图形符合模型求解结果。

2 多元协同治理的进一步探讨

通过上述对互联网信息服务业多元协同治理基础博弈模型的探讨，我们可以发现，总的来说，提高协会与公众参与度水平，有助于博弈系统朝着理想状态（1，1）点演化，但在对系统不同稳定状态进行关联研究时，发现协会与公众的参与对博弈主体的决策选择并非一定起到积极作用。这表明协会与公众在互联网信息服务业多元协同治理过程中的影响是一个复杂的过程。

结合行业实际情况，我们可以发现其原因主要包括以下两个方面：第一，协会是由政府主导，行业内部自发形成的，因此协会在治理过程中作用的发挥除了受到参与度的影响，还跟其自身在治理过程中的权利大小有关系；第二，公众作为一个私人单位，其获取企业相关信息的渠道受限，对于企业行为性质的判断也容易出现主观性错误，从而使得其举报出现失真现象，进而影响行业治理效果。

2.1 参数优化及模型调整

2.1.1 参数优化

基于对现实情境的分析，笔者新增了三个参数，ω：协会的权力空间（0＜ω＜1），其中ω＝0表示协会在治理过程中的作用被政府部门完全限制；ω＝1表示协会在治理过程中拥有极大的自主能力。φ：公众举报公正程度（0＜φ＜1），其中φ＝0表示公众举报企业得到信息是不公正的，即企业采取了合规行为，公众却向政府部门举报企业存在违规行为：φ＝1表示公众向政府部门的举报信息是完全客观、公正的，能够很好地反映企业在市场行为中的真实情况。θ：政府部门对由企业采取合规行为所提升社会福利的分成比例（0＜θ＜1）。

同时对部分假设进行适当调整。

假设1政府部门积极监管时所需花费的成本不仅与协会参与概率有关，同时还受到协会权力空间大小的影响，即c＝c0+（1-pω）／k。

假设2政府部门会对采取合规行为的互联网信息服务企业进行奖励θm。

假设3当公众的举报信息存在失真现象时，政府部门由于受到谣言的影响，因此其将会面临损失（1-φ）qn，企业由于受到谣言的影响，因此其将会面临损失（1-φ）qδ。

2.1.2 模型调整

根据新增的参数及假设条件，可得调整后多元协同治理博弈模型的收益支付矩阵如表4所示。

表4 收益支付矩阵

其中：c＝c0+（1-pω）／k，μ＝λ+q（1-λ）。

通过求解复制动态方程，并运用雅可比矩阵判断局部稳定性，我们可得此时系统的演化稳定结果，具体分为以下五种情况：

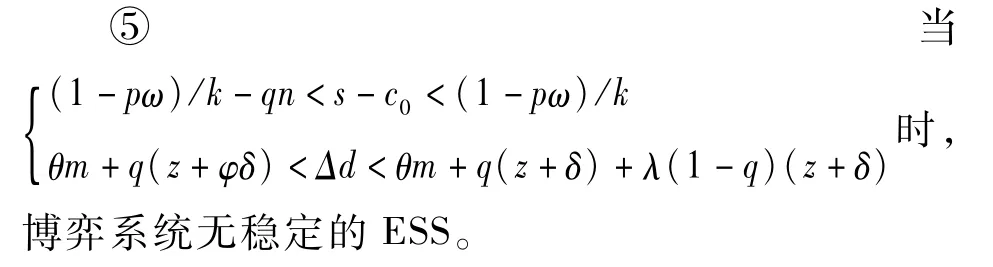
2.2 模型结果分析

为方便分析，且在不影响最终分析结果的基础上，笔者将仅对演化博弈系统趋向于稳定点（1，1）的情形进行分析，其他情形暂不分析。

2.2.1 协会作用分析

（1）协会参与概率p对治理效果的影响分析

将函数F（p，ω）对p求偏导数，我们可以得到如下关系式：∂F（p，ω）／∂p＝-（ω／k）＜0，表明函数F（p，ω）与协会参与概率p呈负相关的关系。因此，为使函数F（p，ω）达到最小，即充分发挥协会在治理过程中的效果，需要政府部门积极引导协会参与治理过程，协助政府实现治理效果的优化。

（2）协会的权力空间ω对治理效果的影响分析

将函数F（p，ω）对ω求偏导数，我们可以得到如下关系式：∂F（p，ω）／∂ω＝-（p／k）＜0，表明函数F（p，ω）与协会权力空间ω呈负相关的关系，即政府部门给予协会的自主能力有利于其在治理过程中发挥作用。因此，为使函数F（p，ω）的值达到最小，需要政府部门给予协会充分的权利，使其能够充分发挥自身作为行业内独立第三方的优势。

2.2.2 公众作用分析

（1）公众参与概率对治理效果的影响分析

将函数H（q，w）对q求偏导数，我们可以得到如下关系式：∂H（q，ω）／∂q＝φδ+z-λz-λδ，可以看到该式的正负性难以确定，跟λ的取值大小有关。因此，下面将针对不同的取值进行分类讨论。

①当λ＞（φδ+z）／（z+δ）时，∂H（q，φ）／∂q＜0，此时函数H（q，φ）与公众参与概率q呈负相关的关系，即在政府部门自身监管能力比较强时，若公众举报存在失真现象，则公众参与治理过程不利于行业治理效果的优化。因此，在此情形下，为使函数H（q，φ）达到最大，实现互联网信息服务业更好地治理效果，政府部门应该采取相应措施，降低公众的参与概率。

②当λ＜（φδ+z）／（z+δ）时，∂H（q，φ）／∂q＞0，此时函数H（q，φ）与公众参与概率q呈正相关的关系，即在政府部门自身监管能力较弱时，即使公众举报存在失真现象，其参与治理仍可以实现行业治理效果的提升。因此，在此情形下，为使函数H（q，φ）达到最大，需要政府部门采取措施积极引导公众参与治理过程。

（2）公众举报公正程度φ对治理效果的影响分析

将函数H（q，φ）对φ求偏导数，我们可以得到如下关系式：∂H（q，φ）／∂φ＝qδ＞0，表明函数H（q，φ）与公众举报公正程度φ呈正相关的关系，即客观、公正的举报对于提升互联网信息服务业的多元协同治理效果具有积极作用。因此，为使函数H（q，φ）达到最大，需要政府部门对公众积极加强正确引导，自觉规范自己的举报行为。

通过对上述协会与公众相关参数在治理过程中的分析，我们可以发现协会参与概率p与协会的权力空间ω，对互联网信息服务业的治理效果保持一致，始终起着积极的促进作用；而在考虑公众在治理过程中的作用时，政府部门需要综合考虑影响多元协同治理模式效果发挥的各方面因素，全面统筹制定相关制度措施，以有效治理互联网信息服务业。

3 结论

政府部门对互联网信息服务业实施多元协同治理，需要积极引导协会与公众参与治理过程，而明晰二者参与概率、自身属性等关键参数对博弈系统均衡策略选择的影响，是切实发挥多元协同治理模式效果的关键环节。本文采用演化博弈理论，通过分析协会与公众各自参数取值变动对系统稳定演化状态的影响，探究政府部门如何有效引导协会与公众参与治理过程，充分发挥多元协同治理模式的积极作用。

结果显示：互联网信息服务业多元协同治理模式的实施是一个复杂的系统过程，为使其作用得到切实的发挥，需要政府部门综合考虑协会与公众在治理过程中的作用，制定合理、实际的制度措施。一方面，政府部门需要利用好协会与公众在治理过程中的协助作用，积极引导协会与公众参与治理过程，履行自身社会职责；另一方面，政府部门要充分考虑其他治理参与主体的局限性，不过度依赖协会与公众的协助作用，努力提升自身监管能力，在互联网信息服务业多元协同治理模式中，始终做好领导者的角色。总之，政府部门应充分利用各参与主体的优势作用，综合考虑影响协会与公众发挥作用的各方面因素，形成共同参与、协作长效的多元协同治理体系，营造一个健康、稳定的行业发展环境。