基于演化博弈的在线社会网络谣言传播行为研究

丁学君，刘思奇

（东北财经大学 管理科学与工程学院，辽宁 大连 116025）

0 引言

网络谣言是指通过网络介质而传播的没有事实依据的带有攻击性、目的性的话语，主要涉及突发事件、公共领域、政治人物、颠覆传统、离经叛道等内容。网络谣言的传播具有突发性且流传速度极快，并且往往含有偷换概念、以偏概全、歪曲事实以及煽动情绪等内容，并在公众“宁信其有、不信其无”以及从众心理等因素的推动下，极易导致“谣言泛滥”现象的发生，从而对正常的社会秩序造成不良影响。目前，微博、微信等在线社会网络已经成为用户信息获取、传播、分享以及好友间交流沟通的主要平台。然而，不同形式的在线社会网络在为人们提供便利的信息互动渠道的同时，也降低了不实信息的传播成本，进而逐渐发展成为网络谣言肆意滋生的温床。

例如，2008年10月，一位十多岁的少年在公民新闻网站CNN Ireport上发帖称“苹果首席执行官史蒂夫·乔布斯突发心脏病”，随后该谣言在Twitter等主流社交网络上大肆传播。尽管最终被证明为虚假信息，但该谣言的迅速传播，导致高度敏感的投资者大量抛售持有的苹果股票，使得苹果公司的市值在瞬间蒸发了90亿美元；“2013年4月23日白宫发生两次爆炸，奥巴马在爆炸中受伤”的谣言，在Twitter上传播，仅仅几分钟就导致100亿美元的损失；2011年3月11日，日本地震后，新浪微博等国内社交媒体上出现“碘盐可防核辐射”、“中国食盐将遭受核辐射污染”等谣言，部分商户看准“商机”，恶意囤积，哄抬价格，引发了一场全国性的碘盐“抢购风波”，市场上一度出现了“盐荒”现象。

可见，在线社会网络中的“谣言泛滥”现象，严重影响了网络信息生态环境的健康状态，使得人们难以在纷繁复杂、参差不齐的信息中找到自己所需的可用信息，从而降低了人们所获信息的质量。尤其是发生突发事件时，如自然灾害、公共卫生以及社会安全事件等，谣言的快速扩散极易引发公众群体性的心理焦虑和恐慌，极大地考验着政府部门的社会治理能力和危机应对能力。

因此，揭示在线社会网络中谣言传播演化的客观规律和内在机理，并给出有效的谣言防控策略，不仅是网络平台管理者和政府相关部门亟待解决的现实问题，也是信息系统及应急管理研究领域要解决的关键科学问题之一。

博弈论主要研究公式化了的激励结构间的相互作用，其通过分析博弈参与者的实际行为和预测行为，探究其优化策略，目前已成为研究具有斗争或竞争性质现象的一种常用的数学理论和方法［1］。在微观传播过程中，人们的行为选择并非完全理性，而是在有限的时间和环境中有限理性选择的结果。演化博弈从生物学角度出发，即自然界中的生物在进行选择时，仅考虑当前情况下的有限利益，在不断试错的过程中演化到最终的稳定状态，称为进化稳定策略（Evolutionarily stable strategy，ESS）。这与谣言传播过程中参与者的行为选择相似。因此在本文中，采用演化博弈的方式来描述谣言传播的微观过程，识别其在微观传播过程中的表现形式和演化规律，更能有效地挖掘相关主体之间的矛盾与平衡，并深入了解不同行为产生的动因与演变，从而制定出更具针对性的网络谣言应对策略。

1 相关研究

近年来，国内外学者侧重于基于传染病模型来研究谣言传播演化的内在机理。Hu等人按照人们对谣言的不同态度对谣言传播者进行划分，并建立传播模型，探究不同态度对谣言传播的影响［2］。Zhao等人采用传染病模型与用户遗忘机制相结合，证明了遗忘机制对网络谣言传播的影响［3］。Jia等人在考虑了传统的谣言传播模型后，结合噪声和时间滞后等机制研究谣言传播规律，其主要探究了谣言传播模型中解的存在性、熄灭性、有界性及平衡性等特点，最后利用实验仿真验证了模型的有效性［4］。然而，以上研究侧重于分析谣言信息传播演化的动力学规律，却忽略了个体面对谣言时的态度及行为差异［5～8］。

基于此，部分学者根据网络谣言传播过程中不同参与主体所扮演的角色，建立媒体与政府、网民与意见领袖的两类主观博弈模型。对民众、企业、媒体平台以及政府等，三方及多方主体参与下的谣言或舆情传播行为进行博弈分析［9～14］。魏芳芳等人对网络虚假信息中，政府、企业和公民三方的演化博弈行为进行了分析，构建了网络谣言三方演化博弈模型，并利用三维立体图，展示了不同策略组合的渐进趋势［15］。张琳等人以罗尔事件为例，基于演化博弈理论，分析了在该起事件中受助人、企业以及网民，在网络舆情“形成—发展—检测”的三个阶段中，其不同演化稳定策略的选择［16］。Fernández-Domingos等人建立了多人囚徒困境博弈模型，并分析了网络信息传播时拓扑结构中每个节点的行为。该研究表明在规模较小的网络中，选择合作是节点的最优策略；反之，对于规模较大的网络，选择不合作是最优策略［17］。

上述研究在对谣言传播过程进行博弈分析时，均是简单地将博弈主体按照其不同社会属性进行分类，如将博弈参与者分为政府、网民、网媒、企业等［13～16］，却往往忽略了现有网络中个体属性差异对网络谣言传播行为的影响。为此，部分学者从微观层面上，对传播主体的行为决策进行了博弈分析。Kermani等人建立了一个完全静态纳什均衡的博弈模型，以描述线下舆情传播过程，其认为舆情传播者的影响力和个人倾向会影响传播者的传播行为［18］。Chu等人建立了影响力和策略的协同进化模型，发现在同一个现实社会系统中，参与者的影响力和声誉会对其最终决策产生影响，其仿真结果也表明，网络中合作程度较大时，整体收益较高［19］。余莎莎等人分析了个体谣言传播概率，并结合传播者自身策略的可变性，建立谣言扩散模型［20］。Zinoviev等人的研究则表明，个体对事件的了解程度，即个体的前期知识储备，会影响网络舆情的传播［21］。

上述文献虽然从微观层面上，对个体的舆情或谣言传播行为进行了博弈分析，但却侧重于探究个体的线下传播行为［18，19］；虽然部分研究考虑到了线上、线下传播行为的差异，却未对个体面对谣言这种特殊类型的舆情信息时，其行为选择的影响因素进行深入的分析，因此无法有效揭示在线社会网络谣言传播演化的内在机理［20，21］。

为此，本文通过分析谣言传播时网民的不同行为，将谣言传播参与者分为传播者和接收者两类，并根据现有文献，定义了谣言传播参与者行为决策的三种影响因素：个人知识储备量［21］、声誉［19］以及影响力［19，20］，进而根据上述三种影响因子构成了谣言传播参与者收益函数。显然，谣言参与者行为选择的不同，会使其收益函数发生变化，从而影响在线社会网络中的谣言传播过程。

2 网络谣言传播的演化博弈模型

本文基于演化博弈理论，提出了一个描述谣言传播过程的博弈模型。该模型假设在传播过程中，每一条谣言传播者（Sender）及谣言接收者（Receiver）都有一个体现其收益的收益函数（U）。本文所定义的谣言参与者收益函数，体现了其在面对谣言时，因采取不同的行动策略而获得的利益大小。由前文可知，该收益函数主要取决于三个方面：谣言传播参与者关于这条谣言的相关知识储备的情况（Knowledge）、谣言传播参与者的个人声誉（Reputation）以及谣言参与者的影响力（Popularity）。基于此，本文给出网络谣言传播行为的影响因素，如图1所示。

图1 谣言传播影响因素

2.1 变量具体含义及归一化

表1给出了本文提出的谣言传播模型中不同变量的含义。

表1 模型中各个变量的含义

2.1.1 传播网络

本文将谣言传播网络假设为无向传播网络，因此，可用无向图G＝（Z，Y）来对其加以描述，其中Z表示无向图中的顶点，即网络谣言传播的参与者；Y表示每个参与者（顶点）之间的连接关系，即网络谣言的传播途径。可见，只要参与者在该网络之中，信息便可顺利传播，如图2所示。

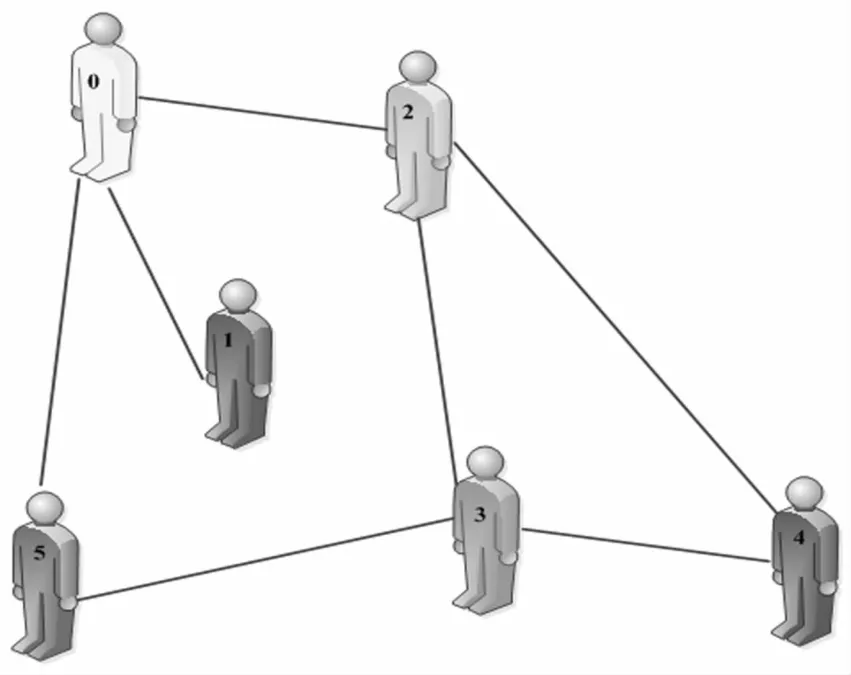
图2 谣言传播网络

本文将网络中谣言传播的参与者分为两类：谣言传播者和谣言接收者。本文认为，若谣言接收者接收到相关谣言，则其可能会对谣言进行回应，如评论、转发、点赞等。方便起见，本文仅将评论行为，作为谣言接收者对谣言产生的回应。通过分析可知，发送方和接收方收益函数中的变量，会随着谣言的传播而发生改变。此时，传播行为的最优策略选择，可以使其收益函数达到最优值。

2.1.2 网络信息总量与自我知识储备

本文假设网络中信息总量为N，其中一名参与者i储备的知识总量为K，即Ki∈N。在全部N条消息中，既包括真实的消息，又包括不实的谣言。值得注意的是，每个参与者对于其知道的所谓的“知识”，并不是一定与客观真相相匹配。也就是说，参与者认为这条消息是正确的，但是客观上该消息不一定正确，也可能是错误的谣言。因此，本文引入一个外部变量φ，用来评判N条信息中为正确信息的概率。考虑到参与者对于消息的真伪判断具有主观性，本文假设其可能具有如下两种状态：①认为消息是真的；②认为消息是假的。

对于任意一个参与者i∈Z，设其知道的信息总量为Ki（Ki∈N），且i主观上认为有个信息为正确的真相，个信息为错误的谣言，则有参与者i主观认为消息是正确的概率为认为消息是错误的谣言概率为

根据以上分析，得到谣言传播初始阶段，参与者i的自我知识储备Ki：

在式（1）的基础上，本文将每个参与者的知识储备均进行归一化，即ki＝Ki／N，并根据每个参与者的知识储备程度ki，将参与者进行分类：如果0.8≤ki≤1，则认为参与者i是一个“明智者”；若0.25≤ki＜0.8，则认为参与者i是一个“平庸者”；若0≤ki≤0.25，则认为参与者是一个“愚笨者”［22］。

2.1.3 声誉

参与者的声誉是指别人对其的信任程度，由网络中与其建立联系的其他参与者进行评判。本文用Ri来表示参与者i的声誉值大小，ri为Ri的归一化值，即ri＝Ri／N。如果一个参与者的声誉值较高，则表明该参与者对信息的评判有较高的可信度；反之，则说明该参与者是一个不可信或不可靠的传播者。例如，若ri＝0.5，则表示对于一条消息，参与者i有50%的可信任程度，即参与者i有50%的概率对消息的判断是正确的。

2.1.4 影响力

每名参与者的影响力是指该参与者在传播网络上受欢迎的程度，本文用Pi来表示参与者i在网络中影响力的大小。Pi值的大小是根据参与者在网络中活跃程度来计算的。如果Pi＝0，则表示该参与者从未在网络中参与传播，甚至在网络中没有人知道他的存在。同理，pi为Pi的归一化，即pi＝Pi／N。本文中认为参与者的影响力随着时间的推移而减少，每单位时间减少δ，且每单位时间恰好是一条信息从传播者发送给接收者的时间。即若参与者i在单位时间内没有发送消息，或者作为接收者没有对信息进行评论，则ΔPi＝-δ。

2.1.5 收益函数

在本文设定的网络中，参与者的自我知识储备（K）声誉（R）以及影响力（P）三个因子互不相关，且不具有多重共线性。本文中假定参与者为有限理性人，会选择当前状况下自我收益函数最大化的策略。在自我知识储备、声誉及影响力的因子前加入系数，表示网络中不同影响因子的重要程度不同，即权重的不同［13］：

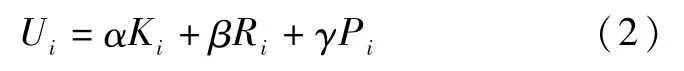
其中α+β+γ＝1，且0≤α，β，γ≤1。当α＝β＝0，γ＝1时，表示一个极端的情况，即参与者并不重视知识和声誉，只重视自身的影响力，即为了最大化自己的影响力，尽可能的向外部发送信息，例如微博网络中的营销号，在“热度至上”的原则下开展营销活动。α＝0.45，β＝0.45，γ＝0.1时，表示一些有名誉、有知识，但不重视自己影响力的参与者，比如一些专注于发表科普类知识的博主等。

2.2 传播过程中收益函数的变化

当网络中出现一条谣言时，谣言传播者可以选择是否传播该谣言；谣言接收者在接收到谣言时，可以选择是否对该条谣言进行评论。根据谣言传播者和谣言接收者选择策略的不同，收益函数也不同。谣言传播过程如图3所示。

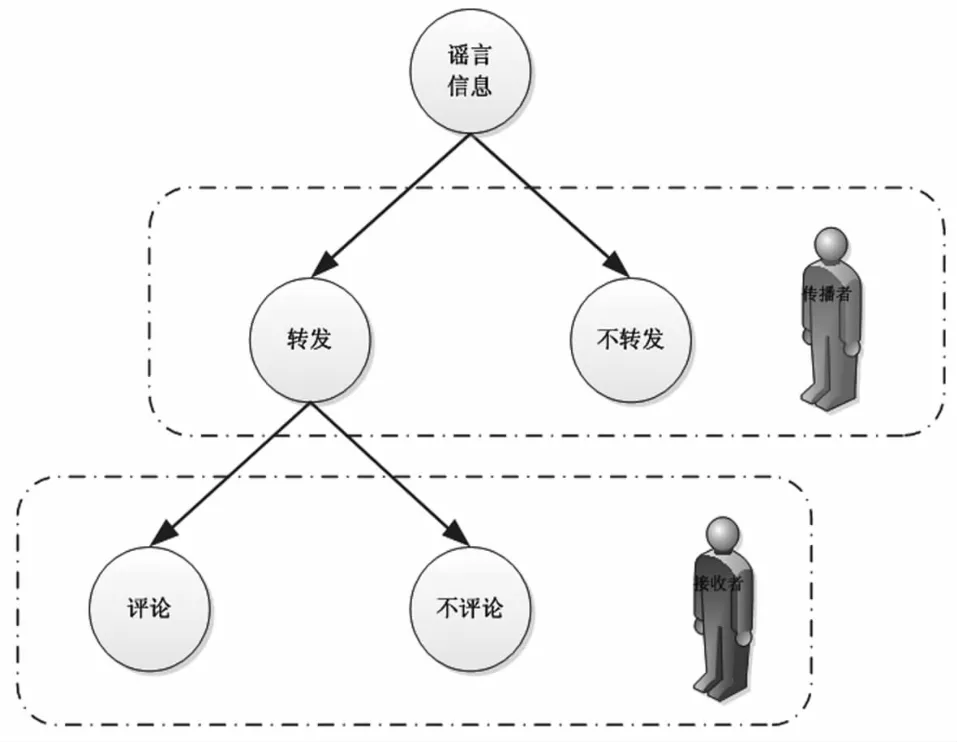
图3 谣言传播过程

2.2.1 谣言信息传播假设

为了建立网络谣言传播行为的演化博弈模型，本文做出如下假设：

（1）谣言传播网络为在线社会网络：本文研究的网络均为在线社会网络，在此前提下，信息才能快速且无成本传播。

（2）信息传播具有反馈及时性：若信息传播的反馈不及时，很容易造成即使发生利益冲突，也因为不能及时传播而不具备博弈条件。

（3）信息本身具有一定的不确定性：本文假设对于给定的传播网络，一定存在谣言，且对谣言的判定具有一定程度的不确定性。在此背景下，才能够出现博弈双方为了各自利益而进行博弈的情况，否则收益函数中的三个影响因子将不会成立。

2.2.2 自我知识储备的变化

当谣言传播者决定传播该条谣言时，谣言接收者可以通过以下几个方式判断是否给予谣言正面或负面的评论。本文认为谣言接收者对谣言传播者发送的消息进行评论时，主要考虑以下三个方面的因素：

（1）接收者根据自身的知识储备对本条谣言作出的判断；

（2）由客观事实所表现出的所传播信息为谣言的概率；

（3）接收者考虑到的发送者声誉。

在本文不考虑ki＝0以及ki＝1的极端情况下，当0＜ki＜1时，谣言在从传播者发送给接收者后，可能会产生以下两种情况（其中g表示能否识别出谣言概率，且g＝g++g-＝1）：

（1）接收者识别出该条谣言，认为传播者所发送的消息为真，即发生g+的情况：

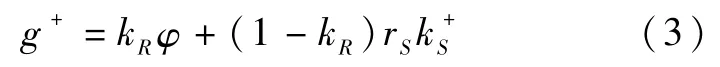
（2）接收者没有识别出这条消息为谣言，即发生g-的情况：

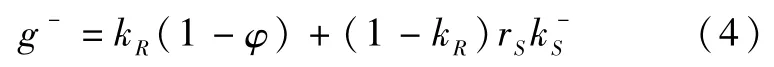
综上，谣言接收者接收到谣言后，谣言接收者的知识储备的改变量为：

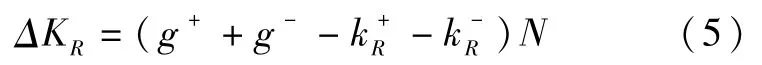
根据ΔKR的变化，对于谣言传播者而言，知识储备量的变化只来源于谣言接收者对信息评论后带来的更改，即：

2.2.3 影响力及声誉的变化

本文认为，只有谣言传播者传播信息，才能维持参与者的影响力；同时，谣言传播者在得到谣言接收者的评论时，作为额外奖励，能够提高自己的影响力，影响力的增加或者减少程度，均为单位时间内（即谣言从传播者到接收者的传播时间）增加或减少δ；但谣言接收者评论与否不改变其影响力。同理，当谣言传播者传播一条谣言时，会降低其声誉，即每传播一条谣言，声誉会相应减少θ［21］。谣言的接收者如果能够正确地识别谣言，并给予谣言传播者一个负面的评价时，则声誉会相应的增加θ；反之，则会减少θ。谣言接收者不对信息进行评论时，其声誉将不发生变化。

综上所述，当谣言接收者在收到谣言后，其影响力的改变为：

当谣言传播者在传播谣言后，其影响力的改变为：

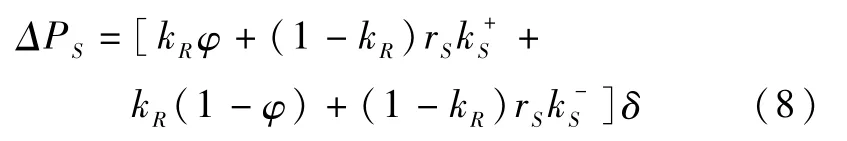
谣言接收者声誉的变化为：

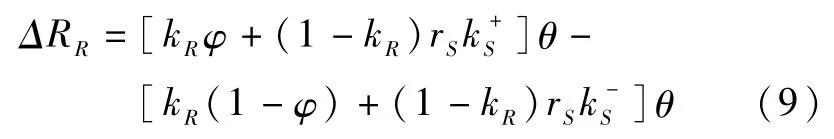
同理，谣言传播者声誉的变化为：

3 谣言信息传播的演化博弈

前文分析了信息在谣言传播者和接收者之间传播的过程。对于网络中每一个谣言传播者和接收者，上述三个影响因子会因为信息的传播而发生改变，从而影响参与者整体的收益函数。本节采用具体的演化博弈模型，探究参与者在不同环境下采取的不同策略，并找出最优策略组合，使参与者最大化自己的收益函数。

3.1 演化博弈收益矩阵

如前文所述，本文假设网络中仅存在两类人，即谣言传播者和谣言接收者，并且该两类群体的特征一致。接下来，本文为上述谣言传播参与者建立博弈模型，行动策略分别为“是否选择传播消息”以及“是否选择给予评论”，其收益函数则为策略选择后得到的收益函数值。本文主要探讨谣言传播演化过程的动态均衡。

前文探讨的收益函数，主要为谣言传播者转发谣言，谣言接收者评论谣言的策略情况。然而，实际上演化博弈模型有四种情况，分别为：

（1）谣言传播者转发谣言（S1），谣言接收者评论谣言（R1）：此时谣言传播者的收益函数为前文讨论的收益函数变化量ΔUS，谣言接收者的收益函数为前文讨论的ΔUR。

（2）谣言传播者转发谣言（S1），谣言接收者不评论谣言（R2）：此时谣言接收者没有评论传播者，因此谣言传播者的知识储备量不变，只有名誉和影响力影响了收益函数。由于谣言传播者转发谣言，因此名誉下降，影响力上升，其收益函数改变量为-ΔRS+ΔPS＝-βθ+γδ。而谣言接收者因为没有进行评论，因此名誉和影响力都没有改变，只有自我知识的储备量发生了变化，其收益函数改变量为ΔKR。

（3）谣言传播者不转发谣言（S2），谣言接收者评论谣言（R1）：此时逻辑上不成立，这种情况不存在。

（4）谣言传播者不转发谣言（S2），谣言接收者不评论谣言（R2）：此时谣言传播者未转发谣言，其名誉和知识储备不变，但传播者在信息传递的单位时间内未转发任何消息，因此影响力下降，收益函数改变量为-ΔPS＝-γδ。谣言接收者状态没有改变，收益函数改变量为0。根据以上分析，得到谣言传播者与转发者的博弈关系矩阵，如表2所示。

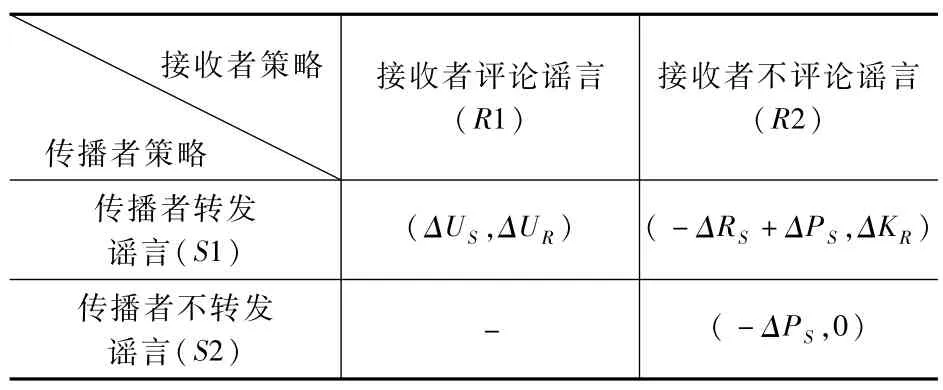
表2 传播者与转发者博弈情况

3.2 谣言传播者与谣言接收者博弈的均衡分析

博弈初始阶段，假设谣言传播者群体中选择“转发”的概率为x，选择“不转发”的概率为（1-x）；谣言接收者群体中选择“评论”的概率为y，选择“不评论”的概率为（1-y）。

（1）谣言接收者“评论”与“不评论”的期望收益及群体平均收益，分别为G1Y、G1N和G1，则：

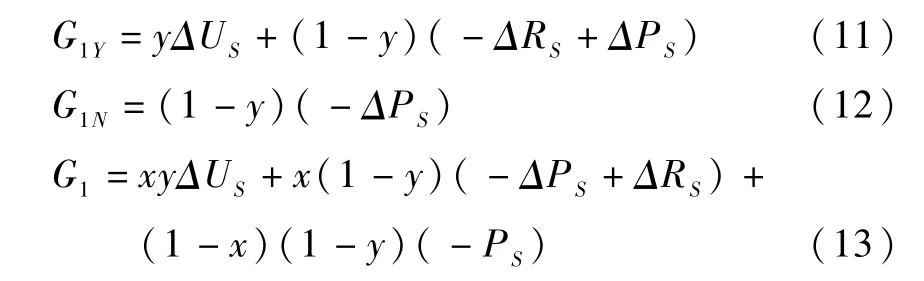
（2）谣言接收者“评论”与“不评论”的期望收益及群体平均收益，分别为G2Y、G2N和G2，则：

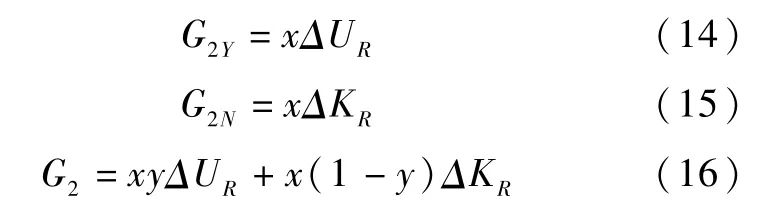
3.3 复制动态方程

3.3.1 谣言传播者“转发”概率的复制动态方程

构成谣言传播者“转发”概率的复制动态方程为：

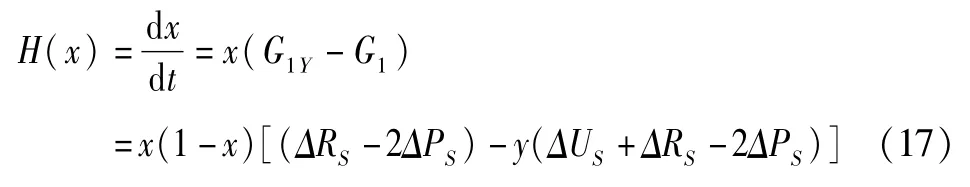
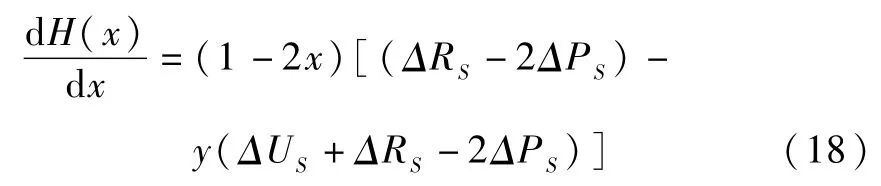
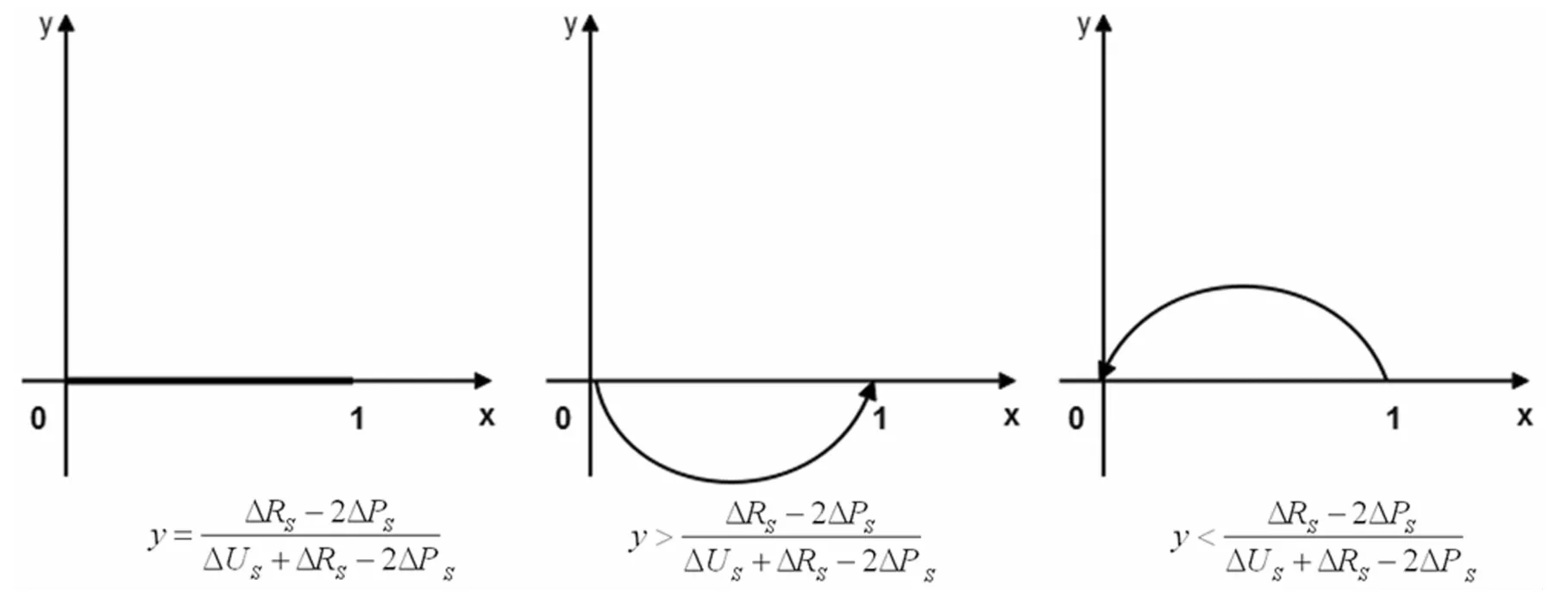
图4 谣言传播者群体复制动态相位图

进化稳定策略［23］要求＜0，通过比较的关系，以下分三种情况进行讨论：

（3）有ΔRS-2ΔPS＜0，ΔUS＞2ΔPS-ΔRS，有则x＝0是进化稳定策略。

由上述分析，得到谣言传播者群体复制动态相位图，如图4所示。

3.3.2 谣言接收者“评论”的复制动态方程

构成谣言接收者“评论”概率的复制动态方程为：

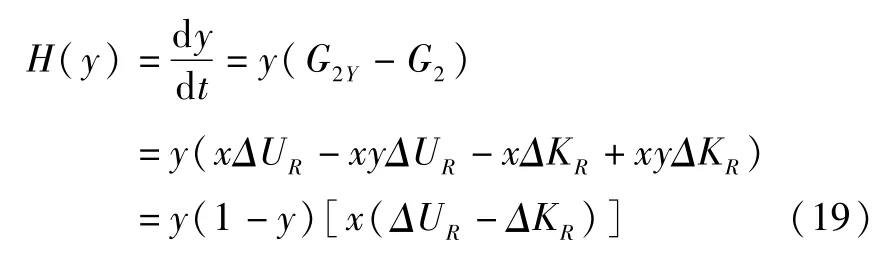
（1）若ΔKR-ΔU＝0时，H（y）≡0，这说明此时所有水平都是稳定的。

（2）若ΔKR-ΔKUR≠0时，令H（y）＝0，得y＝1或y＝0是y的两个稳定状态，此时对H（y）求导得：

由上文可知，当进化稳定策略成立时，有两种情况：

（1）当ΔUR-ΔKR＞0，且y＝0时，＜0，所以此时y＝1是平衡点。

（2）当ΔUR-ΔKR＜0，且时，＜0，所以此时y＝0是平衡点。

由上述分析，得到谣言接收者群体复制动态相位图，如图5所示。

图5 谣言接收者复制动态方程相位图

3.3.3 博弈均衡状态

通过上述对于该非对称复制动态进化博弈的求解，可以得到以下均衡状态，如图6所示：

（1）当初始状态落在区域1时，若ΔUR-ΔKR＞0，则x＝1，y＝1，即（转发，评论）是谣言转发者和接收者，谣言传播博弈的结果。

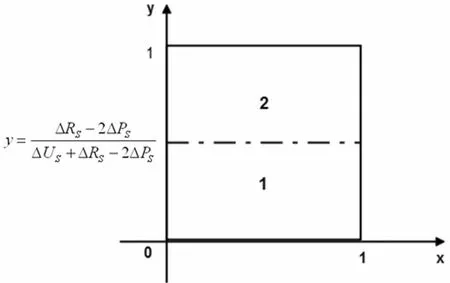
图6 谣言两群体进化博弈坐标示意图

（2）当初始状态落在区域1时，若ΔUR-ΔKR＜0，则x＝1，y＝0，即（转发，不评论）是谣言转发者和谣言接收者，谣言传播博弈的结果。

（3）当初始状态落在区域2时，若ΔUR-ΔKR＜0，则x＝0，y＝0，即（不转发，不评论）是谣言转发者和谣言接收者，谣言传播博弈的结果。

4 博弈结果分析

4.1 博弈模型求解结果分析

通过上述对谣言传播者和谣言接收者群体的动态趋势的求解与分析，比较不同的均衡结果，可以得出以下结论：

（1）如果出现ΔKR-ΔUR＞0且此时ΔUS＜2ΔPS-ΔRS，（谣言传播者的收益函数由、和三部分组成，因此可以将谣言传播者稳定策略的条件简化为ΔKS＜ΔPS），此时x＝1，y＝1是稳定策略，即谣言传播者知识储备的收益，小于影响力的收益时，谣言传播者会采取“转发”的策略；而对于谣言接收者，则是整体的收益小于谣言接收者知识储备方面的收益时，谣言接收者在得到消息时会采取“评论”的措施。

（2）ΔKR-ΔUR＜0，此时y＝0是稳定策略，即当谣言接收者在接收到谣言时，接收者单方面知识储备增长的收益，小于谣言接收者整体的收益时，谣言接收者接收到消息后会采取“不评论”的措施。

（3）ΔUS＞2ΔPS-ΔRS，此时x＝0是稳定策略。即谣言传播者知识储备的收益大于影响力的收益时，谣言传播者会采取“不转发”的策略。

4.2 仿真结果及其分析

本文所描述的谣言传播的纯策略演化博弈中，博弈的参与者，即谣言的传播者以及谣言的接收者，只有两种策略选择。当外界条件改变时，博弈双方会从一种均衡状态演化为其他均衡状态。

为进一步描述谣言传播博弈的演化过程，本文采用MATLAB对博弈过程进行了仿真，如图7～14所示。其中横轴为复制动态方程中步长的变化，即信息传播时间；纵轴为进化稳定时，参与者的策略选择。

本文中仿真参数为全网络不同影响因素的权重，因此针对谣言传播者和谣言接收者的权重系数未加以区分。

4.2.1 知识储备对谣言参与者策略选择的影响

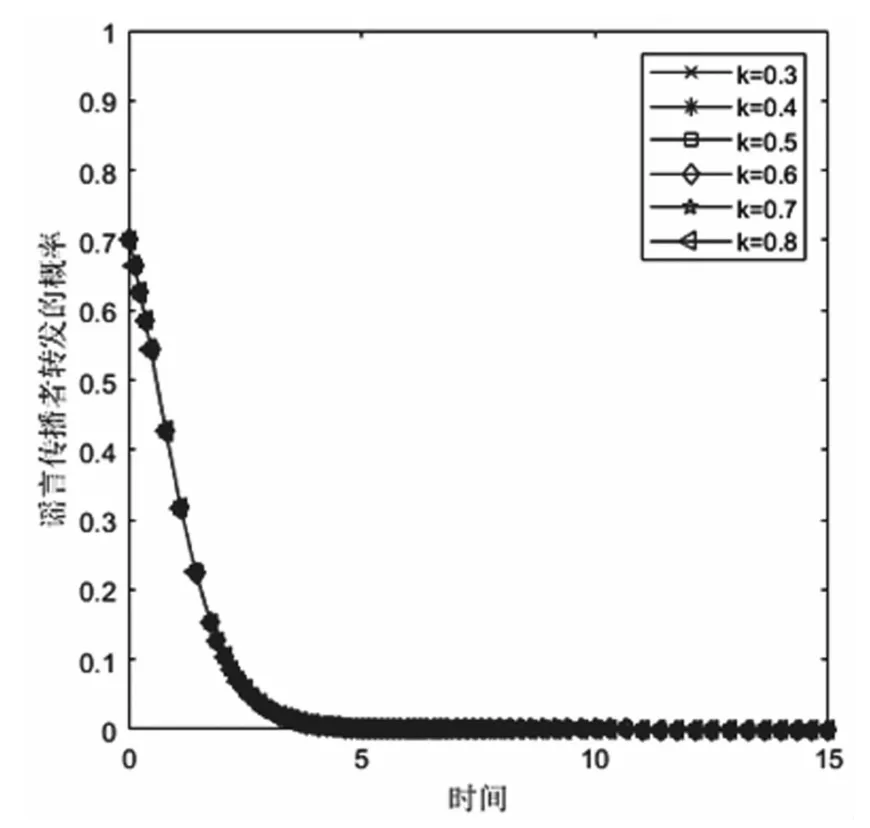
图7 网络中知识储备量权重较大时，初始知识储备量变化对谣言传播者策略选择的影响

图7给出了当网络中知识储备量权重较大时，谣言传播参与者初始知识储备量K的变化对其策略选择的影响，仿真中采用的谣言参与者初始知识储备量参数为归一化后的值，即k。其中参数分别设定为：知识储备量权重α＝0.7；声誉权重β＝0.15；影响力权重γ＝0.15。

由图7和图8可得如下结论：

（1）对谣言传播者的影响

当网络中知识储备量权重较大时，不管谣言传播者初始知识储备量取值如何，其策略选择趋向一致，即谣言传播者转发的概率随着时间推移逐渐降低，并最终稳定为0。由此看出，谣言传播者的转发意愿逐渐降低，最后稳定于选择不转发谣言的策略。这是由于ΔKS＞ΔPS，谣言传播者知识储备的收益，大于影响力的收益时，谣言传播者会采取不转发的策略。

（2）对谣言接收者的影响

当网络中知识储备量权重较大时，谣言转发者评论的概率随着时间推移逐渐增加，并最终稳定为1。由此看出，随着时间推移，谣言转发者评论的意愿逐渐降低，最后稳定于选择评论谣言的策略。这是由于ΔKR-ΔUR＞0，接收者单方面知识储备增长的收益，大于谣言接收者整体的收益时，谣言接收者接收到消息后会采取评论的措施。

图8 网络中知识储备量权重较大时，初始知识储备量变化对谣言接收者策略选择的影响

4.2.2 当网络中声誉权重较大的情况

图9给出了当网络中声誉权重较大时，谣言传播参与者初始声誉值R的变化对其策略选择的影响，仿真中采用的谣言传播参与者初始声誉参数为归一化后的值，即r。其中参数分别设定为：知识储备量权重α＝0.15；声誉权重β＝0.7；影响力权重γ＝0.15。

由图9和图10可得如下结论：

（1）对谣言传播者的影响

当网络中声誉权重较大时，不管谣言传播者声誉取值如何，其策略选择趋向一致，即谣言传播者转发的概率随着时间推移逐渐增加，并最终稳定为1。由此看出，随着时间推移，谣言传播者的转发意愿逐渐增加，最后稳定于选择转发谣言的策略。这是由于ΔUS＜2ΔPS-ΔRS，谣言传播者总体函数收益小于两倍的声誉与影响力的差值，谣言传播者采取转发的策略。

（2）对谣言接收者的影响

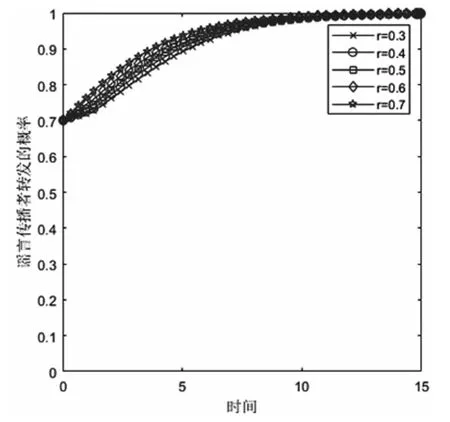
图9 网络中声誉权重较大时，初始声誉变化对谣言传播者策略选择的影响

当网络中声誉权重较大时，谣言转发者评论的概率最终稳定为1。随着时间推移，谣言转发者评论的意愿逐渐增加，最后稳定于选择评论谣言的策略。谣言接收者在评论谣言时，会增加其声誉从而导致收益函数的增加。因此谣言接收者接收到消息后会采取评论的措施。

图10 网络中声誉权重较大时，初始声誉变化对谣言接收者策略选择的影响

4.2.3 网络中影响力权重较大的情况

图11给出了当网络中影响力权重较大时，谣言传播参与者初始影响力P的变化对其策略选择的影响，仿真中采用的谣言传播参与者初始声誉参数为归一化后的值，即p。其中参数分别设定为：知识储备量权重α＝0.15；声誉权重β＝0.15；影响力权重γ＝0.7。

由图11和图12可得如下结论：

（1）对谣言传播者的影响

当网络中影响力权重较大时，随着时间的增加，谣言传播者转发的概率随着时间推移逐渐增加，并最终稳定为1。由此看出，随着时间推移，谣言传播者的转发意愿逐渐增加，最后稳定于选择转发谣言的策略。这是由于ΔKS＜ΔPS，即谣言传播者知识储备的收益，小于影响力的收益时，谣言传播者会采取转发的策略。

（2）对谣言接收者的影响

当网络中影响力的权重较大时，谣言接收者的评论概率与初始值增加，谣言接收者的策略选择则倾向于增加自己选择评论的可能性。这是由于ΔKR-ΔUR＜0中其他相关参数变化不确定的情况下，评论谣言能够带来更高的收益，但由于网络中影响力占比较大，收益增长不显著。因此谣言转发者更倾向于评论的策略。

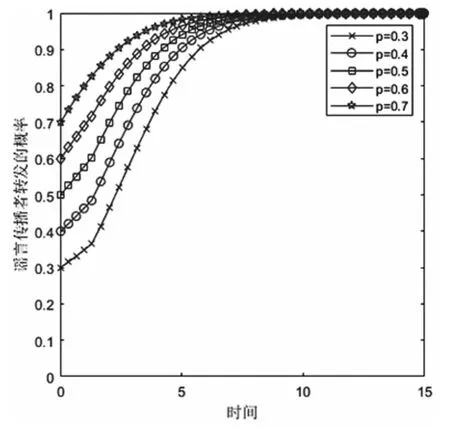
图11 网络中影响力权重较大时，初始影响力变化对谣言传播者策略选择的影响

图12 网络中影响力权重较大时，初始影响力变化对谣言接收者策略选择的影响

4.2.4 网络中三种影响因子的权重系数相同

图13给出了当网络中三种影响因子的权重系数相同时，谣言传播者参与者的策略选择情况，其中参数分别设定为：知识储备量权重α＝1／3，声誉权重β＝1／3，影响力权重γ＝1／3；不同的曲线初始取值具有随机性，取值范围为［0，1］。

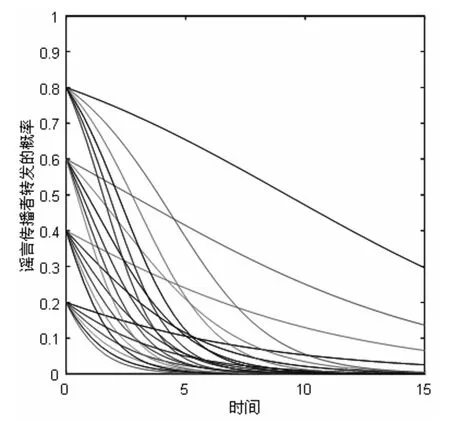
图13 网络中三种影响因子权重相同时对谣言传播者策略选择的影响

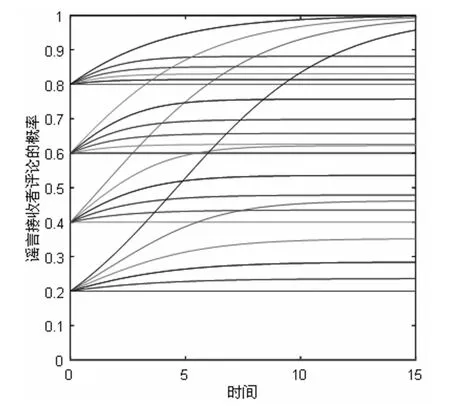
图14 网络中三种影响因子权重相同时对谣言接收者策略选择的影响

由图13和图14可得如下结论：

（1）对谣言传播者的影响

当网络中三种影响因子的权重系数相同时，由仿真结果中策略选择可知，大部分谣言传播者采取了不转发的策略。这与由复制动态方程得出的演化稳定策略的结果一致，即在进化稳定策略中，知识储备和声誉趋向相同，且均占比较大时，谣言传播者倾向于不转发谣言的策略。

（2）对谣言接收者的影响

当网络中三种影响因子的权重系数相同时，谣言接收者的策略选择倾向于增加评论的概率。这是由于复制动态方程中所得出的进化稳定策略分别与x＝0和收益函数ΔUR有关，而谣言接收者选择评论时带来的收益大于不评论。因此，谣言接收者的策略选择倾向于增加评论的概率。

4.3 控制网络谣言传播的策略建议

本文根据得到的三种进化稳定策略，提出以下控制在线社会网络谣言传播的建议：

（1）由4.2节的仿真结果可知，当三种影响因子中，影响力权重不具明显优势的情况下，谣言接收者均选择“不转发”谣言的行动策略。可见，降低网络中影响力权重，对谣言传播起到一定的抑制作用。因此，网民应该减少对网络中不考虑事实真相，而仅以传播公众感兴趣的新奇信息来“博取眼球”的用户的关注，降低其在网络中的整体影响力，进而减少其传播谣言的收益，达到净化网络的目的。

（2）当谣言传播者采取“转发”策略时，只有当谣言接收者有足够的知识储备时，才能够保证自身收益函数的增长大于知识储备的增长，谣言接收者才能识别谣言。因此，网民应该自觉提高自己的知识储备量，自觉遵守互联网的准入标准，提升自我修养和网络素质，进而可以在接触到谣言时，具有一定的甄别能力；同时，在接收到谣言时，网民也应该积极发布辟谣评论，扩大其他网民针对该条谣言的知识储备量，使谣言不能多方位、大范围的传播。

（3）谣言传播者采取“转发”策略，通常情况下是由于谣言转发者影响力的收益增长，大于了谣言转发者知识储备量的增长。上述情况在当今互联网上也非常普遍，比如一些营销号为了扩大影响力，增加阅读量，在转发消息时不进行信息甄别。这些转发者都有一些共有特征，譬如转发数量大、题目吸睛等。针对以上情况，本文建议国家出台相关的法律法规，对这些无良的转发者进行监管，同时互联网平台也应该通过后台的数据特征分析，对这些转发者采取诸如“封号”或者“禁止准入”的措施来净化互联网环境。

（4）从本质上来看，谣言传播者策略为“不转发”，是因为收益函数中声誉与知识储备的权重占比较大。因此，想要杜绝谣言的无序传播，还要靠互联网参与者的个人努力。为此，可以对网络中有较好的声誉和知识储备的互联网用户，给予适当的鼓励和认可，同时每个互联网参与者也应该积极倡导“网络正能量”，为维系健康的网络生态环境做出努力。

5 结语

深入分析在线社会网络用户在面对谣言时的心理及行为选择，将有助于揭示网络谣言传播的内在机理，从而为有效遏制网络谣言扩散提供重要的理论依据。为此本文基于演化博弈理论，对在线社会网络谣言传播行为进行深入分析。本文首先建立了网络谣言传播模型，该模型主要从三个方面考虑了谣言传播者以及谣言接收者的个人特征：自我知识储备、声誉以及影响力。本文假设以上三个特征会影响谣言传播者及接收者的行为决策，因此基于上述三个影响因子，建立了谣言参与者的收益函数，且每个参与者都想最大化自己的收益。在谣言传播过程中，谣言传播者的策略为“是否转发该条谣言”，而谣言接收者的策略为“在看到该条消息后是否予以评论”。由于谣言转发者和谣言接收者在选择不同策略时，会对自身的收益产生影响，因此本文建立了一个演化博弈模型，用来描述谣言传播中的策略选择过程。该模型中，如果两个谣言参与者选择策略不同，将导致其收益函数不同。在不考虑环境中其他人影响的情况下，作为有限理性人的谣言传播参与者，将选择使自身当前收益最大化的策略。此外，本文通过对演化博弈动态方程的求解，找到了谣言传播博弈的进化稳定策略，并利用MATLAB对谣言传播过程与三种影响因子之间的关系，进行了仿真分析。分析结果表明：网络用户更加重视知识储备量和声誉时，将不利于谣言传播。最后，本文根据分析得到的不同稳定策略，进一步给出控制谣言传播的策略建议。

本文未来可能的研究方向包括：1）本文将网络中的用户群体划分为谣言传播者及接收者，并假设两个群体中每个参与者的特征函数权重相同，即在同质网络假设下，建立谣言传播的演化博弈模型。下一步，本文则拟对异质网络中的谣言传播行为进行博弈分析。2）分析表明，参与者具有的复杂心理特征，会对其谣言传播行为造成影响，因此未来将会对影响谣言传播行为决策的多方面因素进行深入分析，从而对模型进一步地完善和改进。