基于非线性压缩估计的投资组合优化模型在A股市场的实证

田楚杰 武汉大学经济与管理学院

当前我们所熟知的投资组合理论是以Markowitz证券组合理论为基础，该理论的主要方法是建立了投资组合的二次规划模型，同时利用效用函数理论提供了使用无差异曲线在投资组合有效集上选择最佳投资组合的方法。Markowitz投资组合的选取在实践中的关键之处在于需要估测期望收益向量以及收益率的协方差矩阵。

Merton（1980）指出，资产收益率均值的估计误差对投资组合最优权重有着更大的影响，现在大多研究多采用最小方差投资组合模型，其只需要估计出资产收益率的协方差矩阵。估计协方差矩阵的一种重要思路是使用压缩估计量，Ledoit和Wolf（2013，2014，2017b）分别提出了协方差矩阵的线性压缩估计量和非线性压缩估计量，本质是将样本协方差矩阵的特征值进行压缩。Ledoit and Wolf（2017b）发现非线性压缩估计量在美股市场的投资组合优化中取得了极佳的样本外表现，本文主要是检验该方法在中国A股市场的表现。

一、模型

（一）全局最小方差投资组合模型

最小方差投资组合模型由于只需要估计资产收益率的协方差矩阵，且相对于均值-方差模型有着较好的表现，逐渐引起了许多学者的兴趣。最小方差投资组合模型由优化（1）给出：

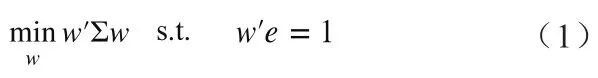
（二）协方差矩阵的压缩估计法

压缩估计是一种非常重要且有效的协方差矩阵的估计方法，尤其是对高维协方差矩阵而言。Ledoit and Wolf（2004b）提出了以单位矩阵作为目标矩阵进行压缩。具体来说，线性压缩估计量是寻找最优的ρ1、ρ2，使得二次损失函数的期望最小，即：

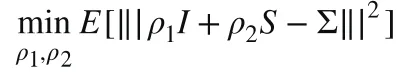
该优化问题也可以求出显式解：

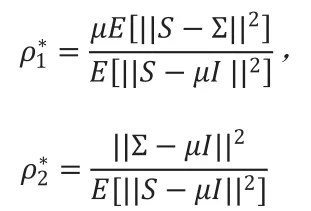
由于总体协方差矩阵∑并无法得知，所以Ledoit and Wolf（2004b）给出了一致估计量对上式的压缩权重进行估计。

线性压缩估计量对样本的所有特征值基于相同的压缩密度，但是当高阶效应比较明显时，该方法并不能有效地改善样本协方差矩阵的误差。所以Ledoit and Wolf（2017b）提出了非线性压缩估计法来估计协方差矩阵，对样本协方差矩阵的不同特征值赋予不同的压缩密度，从而实现样本协方差矩阵的非线性压缩。

Ledoit and Wolf（2011，2012，2014a，2014b）证明了协方差矩阵的 Oracle 估计量：

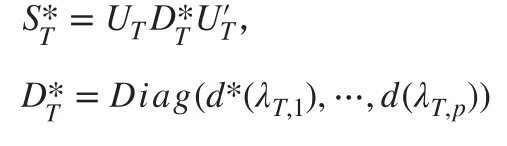
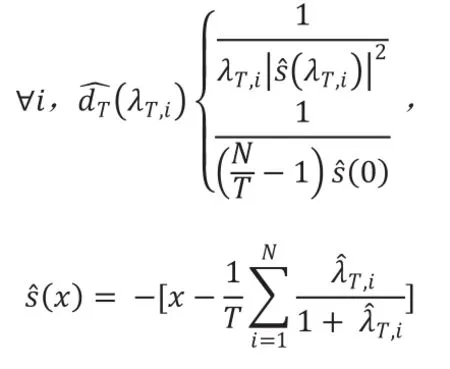
综合来说，压缩估计法从线性压缩发展到非线性压缩，其对样本协方差矩阵的估计误差有更强的调整。不同于线性压缩估计对压缩密度的等同设定，非线性压缩估计赋予不同特征值不同的压缩密度，在高阶效应更为明显的时候表现地更优秀。

二、实证分析

（一）数据

本文的数据来源于CSMAR数据库，包含了 2013 年 1 月 1 日到 2017 年 12 月 31日之间，沪深300的成分股的日收益率数据。

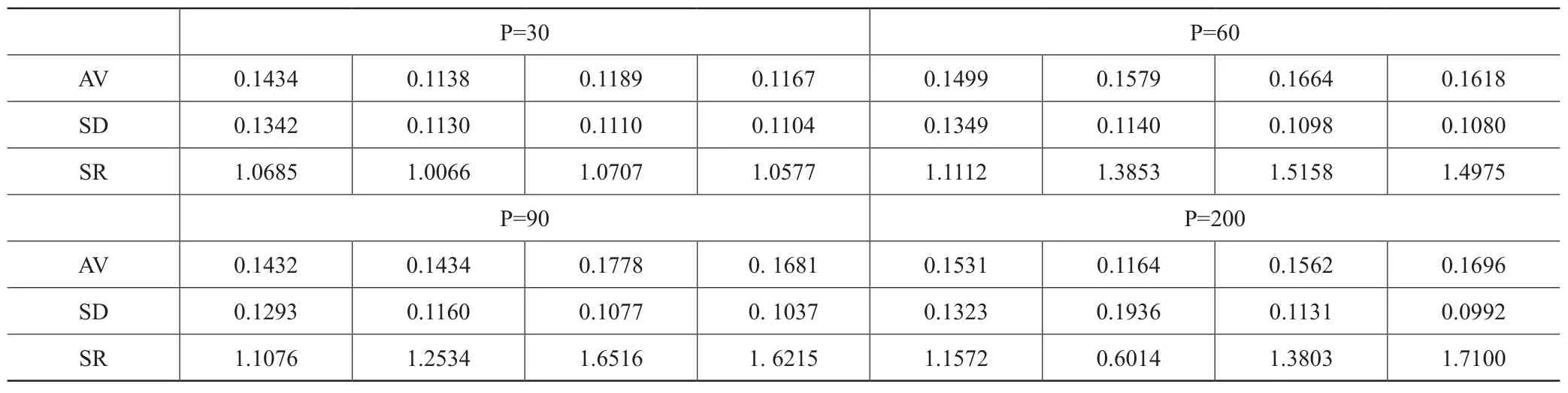
表1 沪深300部分股票的样本外表现

为了简化计算且不失去一般性，我们假定：一个交易月由21个连续交易日组成；且每个月的月初，我们会基于前250个交易日的日收益率数据对下一交易月的持仓进行更新；样本外预测区间为2014年1月1日到2017年12月31日，共48个交易月，即进行了48次投资组合的构建与更新。

此外，为了研究高维效应，我们的组合的大小分别设定为30、60、90、200，即从沪深300成分股分别选择30、60、90、200只股票进行投资。我们在结果中分别报告了投资组合的年化收益率（AV）、波动率（SD）以及夏普比率（SR）。

（二）构建最小方差投资组合

根据优化（1）可以计算出每一个交易月的持仓，我们将比较四种不同的投资组合在该样本下的表现：

（1）EW：等权重投资组合。组合中的每个资产的权重相同。

（2）SP：以样本协方差矩阵作为总体协方差矩阵的估计量。

（3）LS：以线性压缩估计量作为总体协方差矩阵的估计量。

（4）NLS：以非线性压缩估计量作为总体协方差矩阵的估计量。

表1给出了利用沪深300中的30、60、90、200只股票构造的全局最小方差投资组合对应的年化波动率。根据表1的结果可以得到如下结论：

（1）当资产数量较小的时候，四种投资组合的表现较为接近。当资产数量增大时，使用样本协方差矩阵作为总体协方差矩阵的估计量会变得极其不稳定，所产生的投资组合的样本外表现也会变得极差。

（2）当资产数量较小时，线性压缩估计量和非线性压缩估计量所产生的最小方差投资组合的样本外表现相仿。但是当资产数量较大的时候，使用非线性压缩估计法所产生的最小方差投资组合将会在波动率以及夏普率方面表现的显著地更好。

三、结语

本文将协方差矩阵的非线性压缩估计法应用到最小方差投资组合模型中，并在中国A股市场检验其样本外的表现。本文使用了2014年1月1日到2017年12月31日之间沪深300的成分股的日收益率数据，并采用滚动窗口法进行样本外的表现的评估。我们发现，在资产数目较少的时候，采用等权重投资组合，或者样本协方差矩阵、非线性压缩估计量所产生的最小方差投资组合在样本外的表现差别并不是很大。但是当高维效应（即资产数目与估计协方差矩阵所用的时间维度的比值）更加明显时，采用非线性压缩估计量所得到的最小方差投资组合在收益率、波动率以及夏普比率等方面都优于其他方法所产生的投资组合，这说明非线性压缩估计方法应用于最小方差投资组合在中国A股市场也有着重要的意义。