行星车自主探测融合路径规划

郭继峰，于晓强，郑红星，颜 鹏

（哈尔滨工业大学，哈尔滨150001）

1 引 言

随着航天技术的不断发展，各航天大国都相继制定了目标宏伟、各具特色的深空探测计划［1］，在这些计划中，具备自主感知、规划和控制能力的行星车是各国研究计划中的重要组成部分。例如，美国喷气推进实验室提出的全地形六角形地形探测者计划［2］以及美国国家航空航天局（NASA）提出的空间探索飞行器［3］等，旨在开发具备高自主、全地形转移能力的巡视机器人。欧空局火星外空生物学计划拟开发出可以在火星表面自动导航的行星车，用于寻找火星生命过去在火星上的生物标记［4］。日本宇航局和NASA 合作参与阿尔忒弥斯计划，正在共同研发具备超过10000 公里巡视能力的氢动力行星车，以支持未来月球基地建设的计划［5］。我国的嫦娥四号探月工程及天问一号火星探测也分别开发出了具备自主探测能力的行星车。行星车的自主移动及探测能力无疑会给行星探测提供更加自主、鲁棒、高效的探测模式，在深空探测领域具有重要的研究意义。

路径规划技术作为行星车自主探测中最重要的一环，是行星车能够进行安全巡视的必需技术。行星车的路径规划方法可按照环境信息获取手段的不同分为基于离线地图信息的全局路径规划和基于实时传感信息的局部路径规划。

针对行星探测的全局路径规划，文献［6］提出了一种基于月面数字高程地图的大范围自主探测快速安全路径规划算法，在保证路径安全性的基础上加快了搜索速度，提高了月球车自主探测过程的效率及安全性。文献［7］根据履带式和轮式巡视机器人不同的运动特性，分析了行星车自身能力及外部环境约束对规划路径的影响，并对其规划路径进行了评估，验证了方法的有效性。目前全局规划算法着重于在一定评价标准下（如路径长度最短、消耗能量最少等）求解出最优路径，缺少对行星车动力学约束以及路径可行性的考虑。

针对行星探测局部路径规划，文献［8］提出了基于深度强化学习理论的路径规划方法，解决了传统规划算法对先验地图信息的依赖性。该方法直接从传感器信息映射出动作指令，再发布给行星车，仿真实验表明，该算法对不同环境均具有一定的适应性。文献［9］提出基于深度强化学习方法的行星车协同探测方法，可以根据不同的环境调整自身的策略，使行星车具备自学习能力，可以快速有效地探测给定区域。目前局部路径规划主要针对较小区域且考虑精确约束的避障路径规划，缺少对路径全局最优性的考虑，会出现探测结果偏离目标点甚至使全局目标点不可达的情况。

综上，本文提出了一种全局与局部融合的行星探测路径规划方法。首先基于行星表面数字高程模型（Digital Elevation Model，DEM）生成了综合平滑度地图，然后提出了一种融合改进A*算法和动态窗口法的融合路径规划方法，基于综合平滑度信息设计了启发式函数，用于指导A*算法生成全局最优路径，然后应用动态窗口法进行实时路径规划，生成满足行星车能力约束的平滑路径，从而在探测路径全局最优的基础上保证路径可行，提高了行星探测任务的成功性和可靠性。最后选取月球赤道附近地形具有代表性特征的区域作为仿真场景，验证了本文方法的有效性。

2 综合平滑度地图

2.1 地形特征提取

行星表面DEM 地图是获取行星地形信息的主要方式。DEM 数据以栅格形式存储了行星表面每个位置的高程信息，不能直接作为路径规划中的环境地图，需要在DEM 数据中分析提取地形特征。本文主要从坡度、起伏度以及粗糙度三个方面对行星表面的基本地形要素进行分析和提取，采用滚动窗口的形式计算DEM 地图每个栅格内的地形特征，即通过设置一个3×3 大小的滚动窗口，将窗口内的地形信息作为中心栅格的地形特征。

地形坡度θ可由下式计算：

式中，fx、fy为中心栅格东西方向和南北方向高程变化率，采用三阶不带权差分方法计算得到：

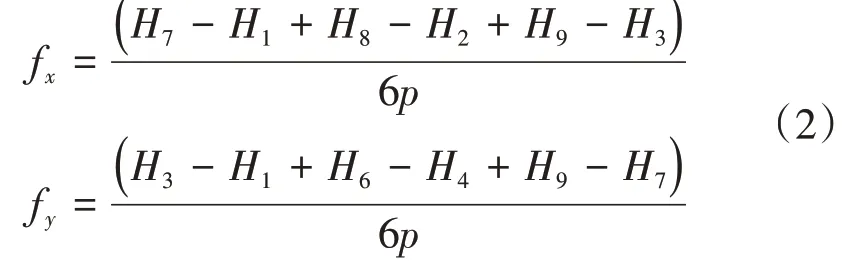
式中，H1～H9分别为3×3窗口内部的9个栅格对应的高程值，p为DEM数据的分辨率大小。

地形起伏度R可由窗口内高程最大值与高程最小值的差计算而来，即：

式中，Hmax、Hmin分别表示窗口内的最大高程值与最小高程值。

地形粗糙度δ可由窗口内所有点的高程值标准差计算而来，即：

式中，Hi为窗口内所有栅格对应的高程值为窗口内所有高程值的平均值。

通过滚动窗口在DEM 地图上依次计算，可以得到地图中所有位置的地形信息，为后续生成综合平滑度地图提供地形特征。

2.2 综合平滑度地图生成

为了保证行星车的安全探测，需要根据地形特征和行星车的运动能力来分析地形的可通过性，本节将可通过性分析转化为对地形综合平滑度的分析，地形综合平滑度越高，可通过性越高，否则可通过性越低。本节分别定义了坡度平滑度Sslope、起伏度平滑度Srelief和粗略平滑度Srough，如下所示：

式中，根据行星车运动能力约束，设置最大坡度、起伏度、粗糙度的阈值限制分别为θmax=20°，Rmax=p/2，δmax=p/5。由于行星车在移动过程中要综合考虑坡度、起伏度、粗糙度等各种地形约束，所以本文将综合平滑度Scom定义为三者的最小值：

通过上节计算得到的地图中各点的地形特征，就可计算各平滑度信息，最终生成综合平滑度地图，为后续进行融合路径规划提供参考。

3 融合路径规划

由于行星探测任务的高风险性与高代价性，必须保证路径规划算法的结果具有全局最优性，避免出现探测结果偏离目标点甚至全局目标点不可达的情况。本节选用具有路径最优性保证的A*算法进行改进，首先结合地形综合平滑度信息设计了一种综合代价函数，作为改进A*算法的移动代价估计，最终规划出路径平滑度最优的全局路径。然后应用融合动态窗口算法进行实时路径规划，生成满足行星车能力约束的平滑路径，从而在探测路径全局最优的基础上保证路径可行，提高了行星探测任务的成功性和可靠性。

3.1 改进A*算法

A*即A-Star算法，是一种常用的求解最短路径最有效的启发式搜索方法［10］，根据启发式函数f(n)指导搜索节点的扩展，定义为：f（n）=g（n）+h（n），其中，f(n)是从初始节点经由节点n到目标节点的代价估计，g(n)是在状态空间中从初始节点到节点n的实际代价，h(n)是从节点n到目标节点的估计代价。当启发式函数f(n)满足一致性条件时，A*可以找到最优解。A*算法在扩展搜索过程中，待检测的节点储存在OPEN 表中，而已检测过的节点则储存在CLOSE 表中，然后扩展当前节点n的所有邻居节点加入OPEN 表中，再选择f(n)最小的节点进行扩展，如此迭代直至搜索到目标节点。然后使用父节点储存回溯节点，从目标节点回溯最终路径。具体算法详见算法1。

?算法1:A*算法1. 输入：Map，Start，Goal 2. Openlist=Start//初始化OPEN表3. Closelist=［］//初始化CLOSE表4. f_score（start）=heuristic_safe（Start，Goal）//初始化f（n）5. g_score（start）=0//初始化g（n）6. parent=Map//初始化父节点查询表7. while Openlist≠NULL do 8. current=the node in openlist having the lowest f_score value 9. if current=goal//到达目标节点10. return reconstruct_path（parent，current）11. end 12. Openlist.Remove（current）13. Closelist.Add（current）14. for each free neighbor v of current do 15. g_score_temp=g_score（current）+diagonal_dist（current，v）16. if g_score_temp ＜g_score［v］or v not in Openlist 17. g_score［v］=g_score_temp 18. f_score［v］=g_score［v］+heuristic_safe（v，Goal）19. parent（v）=current 20. if v not in Openlist 21. Openlist=［Openlist，v］

22. end 23. end 24. end 25. end 26. return failure 27. function reconstruct_path（parent，current）28. path=［current］29. while current≠Start do 30. current=parent（current）31. path=［path，current］32. end 33. return path

本节结合地形综合平滑度定义了一个综合启发式函数f_com（），指导A*算法进行全局最优路径搜索，最终规划出路径平滑度最优的全局路径，定义为：

式中，g（n）是从起始节点到节点n的实际距离代价，Diagonal_heuristic（）为对角启发式距离函数，也可替换为欧氏距离函数或其他满足一致性条件的启发式函数。αs∈[0，1]为地形权重因子，可以人为设定来调节算法在不同区域、不同场景下的侧重情况，增大αs可以使算法更侧重于选择平坦区域，确保探测安全性，减小αs可以使算法更侧重于选择距离最优路径，确保探测效率。

3.2 动态窗口法

动态窗口法（Dynamic Window Approach，DWA）是一种常用的平面移动机器人在线避障规划算法［11］。其原理是在速度空间(v，ω)中采样多组不同的速度，将搜索空间减小到在动态约束下可达的速度，从而将机器人的动力学特性融入到该方法中。然后预测该速度在一段时间后的轨迹，采用一定的轨迹评价函数对轨迹评价，选择出最优轨迹对应的速度指令，发送给机器人控制系统。DWA 算法的基本思路如下：

（1）速度空间中离散采样

由于在二维采样空间中存在多组速度，需要根据行星车本身的能力约束和环境约束将采样速度控制在一定范围中，具体限制如下：

①自身可达速度的能力限制：

②行星车安全距离限制：

式中，dist(v，ω)是该采样速度下对应轨迹上与最近障碍物的距离，v̇b、ω̇b分别是制动线加速度与角加速度。

③自身加速度限制：

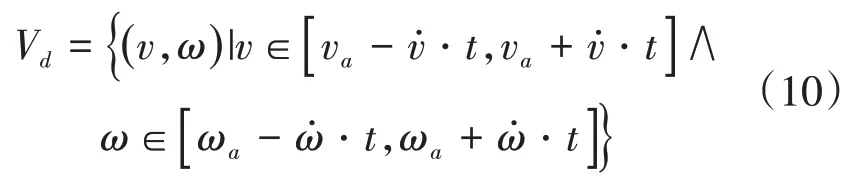
（2）轨迹评价

根据采样得到的速度样本，预测得到的多数轨迹都具有可行性，所以需要设计评价函数对可行轨迹进行评价，选择最优的采样速度组。本节采用的评价函数如下：

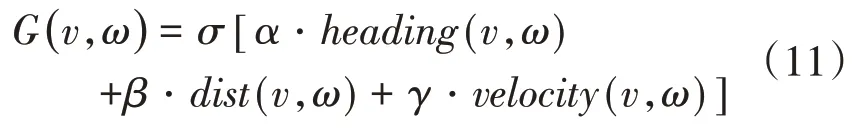
式中：heading(v，ω)是方位角评价函数，评价预测轨迹末端朝向和目标之间的角度差，定义如下：

式中，ω为预测轨迹末端朝向方位角，ωgoal为终点方位角。

dist(v，ω)是安全距离评价函数，表示预测轨迹上与最近的障碍物距离。velocity(v，ω)是速度评价函数，用于评价当前预测轨迹的速度大小；σ为归一化平滑函数，为了防止不同量纲的参数综合导致某项参数占比过高，通过归一化平滑处理得到最终的评价指标，函数形式如下。

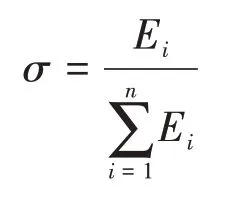
式中，Ei为第i项评估函数的值。

评价函数的作用是选取行星车在避开障碍物的同时以较快的速度朝向目标点运动的最优轨迹。选择评价函数最高的轨迹后，将相关速度作为控制指令控制行星车前进，并在下个步长重复上述过程，最终实现行星车的实时避障规划。

3.3 融合算法

DWA 算法根据行星车检测到的局部窗口环境信息，可实现在线实时规划避障路径。但是，该方法没有考虑路径的全局最优性，存在陷入局部最优的致命问题，故本节融合改进A*算法和DWA 算法进行融合路径规划，以互相弥补全局及局部规划算法存在的主要弊端。

本节根据改进A*算法生成的全局最优路径，设计了DWA 算法的动态窗口评价函数，将动态窗口的目标点设置为与行星车距离最近的全局最优路径点。这样改进使得局部路径规划可以遵循全局最优路径，从而避免了陷入局部最优。融合后算法可以通过修改改进A*算法的地形权重因子调节全局路径的侧重，应对不同的探测需求和地形生成不同的全局最优路径，同时通过修改DWA 算法的参数可以根据行星车能力范围及地形情况调节局部避障路径，最终在探测路径全局最优的基础上保证路径稳妥可行，提高了行星探测任务的可行性和可靠性。

4 仿真结果及分析

4.1 仿真场景

由于行星表面DEM 地图是获取行星地形信息的主要方式，本文采用月球嫦娥二号CE2TMap2015数据集作为行星表面DEM 地图数据代表，验证本文所提方法有效性。首先选取月球赤道附近地形具有代表性特征的区域作为行星车自主探测仿真场景，该区域DEM 地图及地形特征信息如图1 所示，范围约150km×250km（3000×5000栅格）。

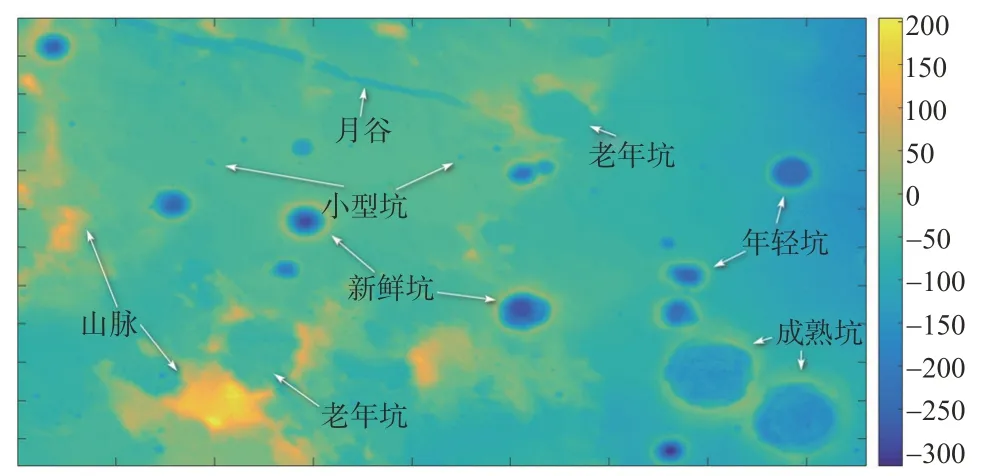
图1 仿真场景DEM地图及主要地形特征Fig.1 The DEM map and main terrain features of simulation scene

本文所有算法的仿真测试软件环境为Windows 10 + MATLAB 2016，硬件环境为Intel（R）Core（TM）i5-7200U CPU+12.0GB RAM。

4.2 综合平滑度地图仿真结果

本节首先根据第二章所提地图处理方法对该区域生成综合平滑度地图，如图2 所示。由图2 可以看出，本节所提出的地形计算方法可以较好的还原行星表面地形特征，对环形山边缘、小型山脉等危险区域有很好的提取效果。并且平滑度地图可以很好地表示出平坦区域（图中较亮区域），为后续路径规划提供参考。

图2 综合平滑度地图Fig.2 Comprehensive smoothness map

4.3 融合路径规划仿真结果

根据上节生成的综合平滑度地图，本节分析本文融合路径规划算法有效性。首先测试改进A*算法中不同地形权重因子对生成路径的影响，本节分别设定以下三种情况进行仿真：路径1：αs= 0.1；路径2：αs= 0.5；路径3：αs= 1。改进A*算法参数设置如下：仿真步长为1栅格（50m），起点（50，50），终点（4950，2950）。DWA 算法参数设置如下：最大线速度为vmax= 1.0m/s，最大线加速度为vamax=0.2m/s2，最大角速度为wmax= 20.0°/s，最大角加速度为wamax= 5.0°/s2，线速度采样间隔为0.01m/s，角速度采样间隔为1.0°/s，时间步长为0.1s，预测步长为2.0s，评价函数参数α= 0.1、β= 0.2、γ= 0.1。仿真结果如图3所示。

由图3 可以看出，融合路径规划算法中，地形权重因子αs较大的路径能更好地选择图中的平坦区域（较明亮区域）。本文对不同地形因子αs情况下算法的性能表现做了对比，结果如表1 所示。可以看出，随着地形因子αs的增大，算法生成的路径长度以及搜索时间变大，但路径整体综合平滑度更好，证明αs可以调节算法的距离最优性和安全最优性，可以在平坦的区域增大αs以增强算法的性能，而在危险的区域减小αs来确保生成路径的安全性。

图3 不同地形权重因子路径对比Fig.3 Comparison of paths under different factors

表1 不同地形权重因子下算法的性能表现Table 1 Performance of the algorithm under different terrain weight factors

本节将融合路径规划算法（αs=1）与标准A*算法，以及JPS算法［12］进行对比，各算法生成路径如图4 所示。由图4 可以看出，相比于其他算法，本文所提出的融合算法搜索出的路径会尽量选择离障碍较远的安全区域，提高了探测路径的安全性。

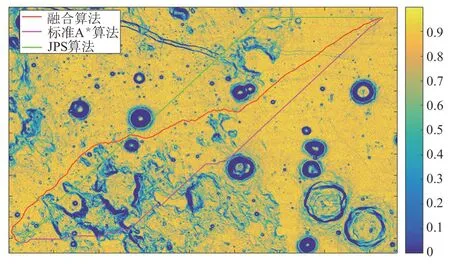
图4 不同算法生成路径对比Fig.4 Comparison of paths generated by different algorithms

本节对比了三种算法的性能表现，如表2 所示。由表2 可以看出，相比于其他两种算法，融合算法生成路径的平均综合平滑度提高大约20%，同时最小平滑度也明显提高，保证了探测过程的安全性。而由于本文所提出的融合算法包括局部实时规划过程，所以算法搜索时间明显高于其他两个全局规划算法，但可保证规划出的路径真实可行，提高了探测任务的可靠性。

表2 不同算法的性能表现对比Table 2 Performance comparison of different algorithms

5 结 论

本文提出了一种基于行星表面数字高程图的行星车自主探测融合路径规划算法，主要得出了以下结论：

（1）根据行星表面DEM地图，分别提出了行星表面地形特征提取方法、综合平滑度计算方法。在此基础上生成综合平滑度图，为后续的融合路径规划提供参考。

（2）提出了改进A*算法和DWA 算法的融合路径规划算法，设计了基于综合平滑度信息的综合启发式函数，可以指导算法根据相关性能生成不同的全局最优路径，并利用DWA 算法生成实时避障路径，保证规划路径真实可行，提高了行星探测任务的成功性和可靠性。最后选取月球赤道附近地形具有代表性特征的区域作为仿真场景，验证了本文方法的有效性。