基于Twistor的航天器领航-跟随编队有限时间姿轨耦合控制

王晨曦，张 勃，白俊强

（1. 中国运载火箭技术研究院，北京100076；2. 西北工业大学无人系统技术研究院，西安710072）

1 引 言

航天器编队可以完成单个航天器难以完成的任务，将不同的功能模块分布在不同航天器上，一方面可以增加系统的容错抗灾能力，另一方面可以降低对运载火箭的要求，降低发射成本［1］。因此，航天器编队飞行技术一经提出，便引领了航天技术发展的趋势，成为研究的热点。近年来，随着对编队控制精度要求的不断提高，六自由度航天器编队的姿轨耦合控制技术得到了广泛关注［2-4］。

对于双航天器领航-跟随编队，采用对偶四元数对航天器的相对位置和相对姿态运动进行统一描述，可以降低六自由度编队姿轨耦合控制律的设计难度，是近几年的研究热点。文献［5-6］用对偶四元数对双航天器领航-跟随编队的六自由度姿轨耦合相对运动进行描述，在此基础上分别提出了终端滑模控制律和快速终端滑模控制律，使航天器编队的相对位置与相对姿态能够在有限时间内收敛到理想值附近，并对控制律进行改进，解决了对偶四元数的二义性问题。文献［7］研究了对偶四元数描述的双航天器领航-跟随编队的六自由度跟踪控制问题，通过自适应律对系统的未知对偶参数和对偶扰动上界进行估计，提出了鲁棒自适应终端滑模控制律。文献［8］根据单位对偶四元数描述的单刚体动力学方程，建立单位对偶四元数表示的单刚体误差动力学方程，然后采用反馈线性化方法设计了单刚体的位置和姿态跟踪控制器，证明了闭环系统的渐近稳定性，并引入切换参数来应对控制过程中可能出现的退绕现象。文献［9-10］应用对偶四元数理论，建立了两个航天器之间的姿轨耦合相对动力学模型，基于对偶四元数的对数运算，提出了双航天器编队不依赖于模型的类PD 姿轨耦合控制器。文献［11］通过引入对偶滤波器，将对偶四元数描述的六自由度刚体的误差动力学系统转换为线性仿射动力学系统，实现了非确定等价快速自适应控制算法，获得了传统确定等价自适应算法不能实现的性能提高。基于对偶四元数描述，文献［12-13］针对航天器的质量和惯性矩阵未知情况，研究了常值未知扰动作用下双航天器领航-跟随编队的六自由度姿轨耦合控制问题，通过设计自适应律估计未知参数和扰动，提出了自适应PD控制律，但是文献［12］所提出的方法不仅计算效率更高，而且能够降低控制能量消耗。文献［14］基于对偶四元数推导了一套挠性航天器的姿轨一体化动力学模型，基于此模型设计了一种自适应位置姿态跟踪控制律，能够在航天器质量特性参数未知的情况下，对其位置和姿态进行跟踪控制，并将控制律应用于挠性双航天器的领航-跟随编队的耦合控制，验证了算法的有效性。文献［15］应用对偶四元数，针对双航天器的相对线速度和相对角速度无法获得的情况，通过引入一个线性时变辅助系统，实现了不依赖线速度和角速度的双航天器领航-跟随编队的姿轨耦合跟踪控制。文献［16］考虑主从航天器的视线角约束，以及从航天器的惯性特性参数未知的情况，在对偶四元数框架下，采用人工势场法对约束进行处理，设计非确定等价自适应律估计航天器的质量和惯性矩阵，提出了约束条件下的双航天器领航-跟随编队的六自由度控制律。

虽然对偶四元数能够对航天器的姿轨运动进行统一形式的描述，但却增加了描述航天器运动的状态变量的维数，加重了计算负担；另一方面，由于描述航天器运动的对偶四元数必须为单位四元数，在有些情况下会带来计算上的困难［17-18］。因此文献［17］提出了用twistor 描述航天器姿轨运动的方法，既能实现姿轨运动的统一描述，简化六自由度控制律的设计，又能克服对偶四元数的缺点。文献［18］对基于twistor 描述的航天器动力学模型设计了无迹卡尔曼滤波器，克服了以对偶四元数为基础难以设计无迹卡尔曼滤波器的困难。针对模块化设计的航天器，文献［19］用twistor 描述两个模块之间的相对位姿运动，并设计了基于twistor 的滑模控制器。文献［20］将twistor 用于描述小行星探测器与固连在小行星着陆点的理想坐标系之间的相对位姿关系，用人工势场法处理小行星探测器着陆过程中的视线角约束和防碰撞约束，提出了满足视线角约束和防碰撞约束的小行星探测器软着陆六自由度控制器。

虽然用twistor 描述航天器的姿轨运动能够克服对偶四元数描述的一些缺点，但是还尚未有基于twistor 的双航天器领航-跟随编队的六自由度姿轨耦合控制器见诸报道。本文基于twistor 描述的双航天器相对姿轨运动方程，提出twistor 框架下的终端滑模控制器，使编队航天器的相对姿轨运动能够在有限时间内收敛到理想状态。本文首先给出用twistor描述的双航天器相对姿轨运动方程。然后提出twistor 框架下的终端滑模面，基于所提出的终端滑模面设计有限时间收敛的双航天器领航-跟随编队的六自由度姿轨耦合控制律，并给出有限时间收敛的证明，接着给出仿真结果，并进行必要的讨论与分析，最后给出本文的结论。

2 航天器相对姿轨运动方程

定义地心赤道惯性系为惯性参考系，原点为地心O，OXI轴在赤道面内指向春分点，OZI轴与地球自转轴重合指向北极，OYI轴与其他两轴构成右手坐标系，记地心赤道惯性坐标系为FI。固连在跟随航天器质心的本体坐标系为FB，坐标轴与跟随航天器的三个惯性主轴重合，构成右手坐标系。坐标系FD为理想坐标系。跟随航天器相对于理想坐标系的相对姿轨运动可以用坐标系FB相对于坐标系FD的相对位姿运动表示，用twistor描述为

图1 坐标系定义Fig.1 Definition of coordinate frames

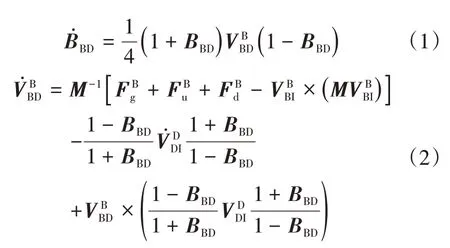
其中，BBD为坐标系FB相对于坐标系FD的twistor，

BBD可以用对偶四元数表示为［17，20］

qBD为坐标系FB相对于坐标系FD的单位对偶四元数，详细定义见文献［17，20］。

为了进一步明确twistor 与修正罗德里格参数（MRP）姿态描述以及质心运动之间的关系，BBD可以写作其中即为坐标系FB相对于坐标系FD的姿态MRP，ΠBD定义为

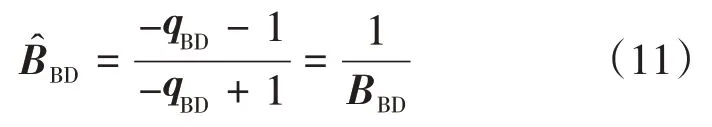
根据四元数和对偶四元数的定义，BBD与表示同一位姿关系［17，20］。

3 终端滑模控制律

为了证明所提出的滑模面和控制律的有限时间收敛性，首先引入如下引理：

引理1.［21］对于任意实数λ＞0，0 ＜r＜1，如果系统的李雅普诺夫函数V满足V̇(x)+λVr(x)≤0，则系统有限时间收敛，收敛时间满足

引理2.［22］对于任意实数λ1＞0，λ2＞0，0 ＜r＜1，如果系统的李雅普诺夫函数V满足V̇(x)+λ1V(x)+λ2Vr(x)≤0，则系统有限时间收敛，收敛时间满足

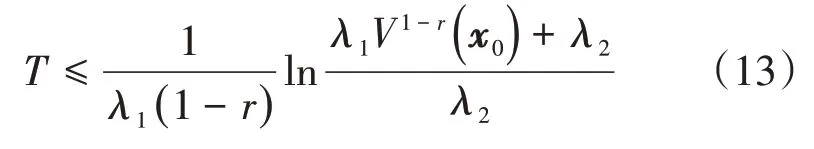
本文提出twistor框架下的终端滑模面为

其中，k1=k1r+εk1d，k1r＞0，k1d＞0，0 ＜γ＜1，

对于滑模面（14），有以下定理：

定理1.对于航天器领航-跟随编队相对动力学系统（1）（2），滑模面（14）在有限时间内收敛至稳定平衡点

证.考虑李雅普诺夫函数Vs对时间求导，得

根据引理1，BBD将在有限时间Ts内收敛到0，Ts满足

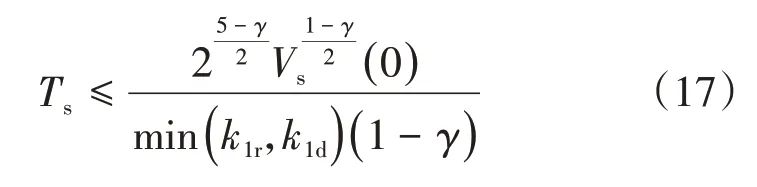
因 此，当 时 间t＞Ts时，ḂBD= 0，由 式（1）得

根据滑模控制器的设计方法，控制量由等效控制和切换控制两部分构成，即

为求得等效控制，首先对S求导，得

式中：

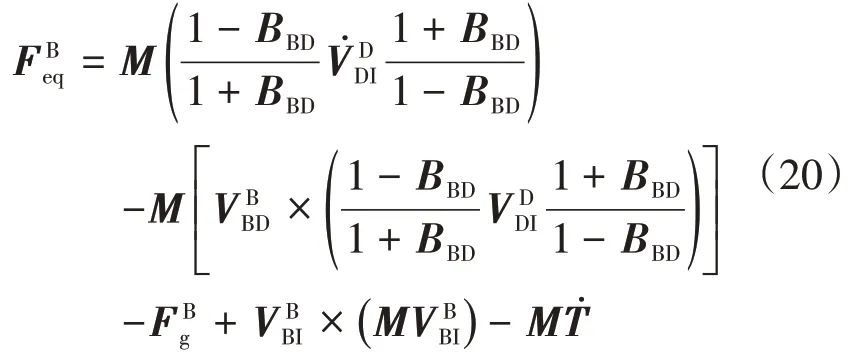
设计趋近律为

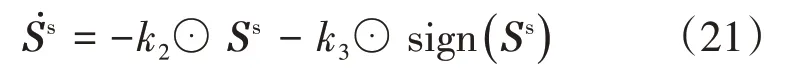
其中，k2=k2r+εk2d，k2r＞0，k2d＞0，k3=k3r+εk3d，k3r≥dr，k3d≥dd，dr为扰动力的上界，dd为扰动力矩的上界。由式（21）可得切换控制项为

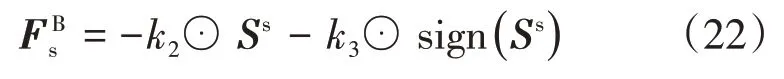
定理2.航天器领航-跟随编队相对动力学系统（1）（2）在控制律（18）的作用下，系统状态在有限时间内到达滑模面（14）。

证.考虑李雅普诺夫函数

对V关于时间求导，得

其中，χ= max(m，λmax(J))，λmax(J)为矩阵J的最大特征值。由于k3r≥dr，k3d≥dd，根据引理2，闭环系统将在有限时间Tr内到达滑模面S= 0，且Tr满足

证毕。

根据定理1和定理2可以得到以下推论：

推论1.航天器领航-跟随编队相对动力学系统（1）（2）在控制律（18）的作用下，系统状态BBD、在有限时间内收敛至稳定平衡点BBD= 0，= 0。

推论1的证明是显而易见的，在此略去。

控制律（18）中包含的符号函数项sign(BBD)会导致控制量的抖振，为了消除抖振现象，本文用sigmoid函数代替sign函数，sigmoid函数定义为

其中，Δ ＞0为小常量。

注1. 在控制律的推导过程中，将BBD视为对偶四元数，包含8 个元素，但是BBD4和BBD8始终为0。因此，在进行数值计算时，完全可以忽略BBD4和BBD8，减少计算量。

注2. 当|BBDi|→0 时，|BBDi|γ-1→+∞，因此由式（19）可知，|BBDi|→0 时等效控制FBeq奇异。在实际情况中，可以设置门限值δ＞0 为一小常量（例如δ= 1× 10-6），当|BBDi|≤δ（i= 1，2，3，5，6，7）时，令|BBDi|γ-1=δγ-1。一旦|BBDi|＞δ，控制律（18）将使BBDi重新进入区域[-δ，δ]。因此，控制律（18）将使BBDi约束在零点的δ邻域内。

4 仿真结果与分析

为了验证本文提出的方法的正确性，本节对所提出的方法进行仿真与分析。图2为坐标系关系。

假设跟随航天器相对于领航航天器的理想位置在领航航天器本体坐标系下表示为-rTDT=[12，0，0]Tm，并且跟随航天器相对领航航天器保持静止，即=[0，0，0]Tm/s；跟随航天器相对于领航航天器的理想姿态用四元数表示为qDT= 0i+0j+ 0.5k- 0.8660，跟随航天器相对于领航航天器的理想角速度为=[0，0，0]T°/s。领航航天器的轨道参数见表1，并且假设领航航天器的本体坐标系始终与当地竖直当地水平坐标系重合。

表1 领航航天器轨道参数Table 1 Orbital elements of the leader spacecraft

跟随航天器的质量m= 50kg，惯量矩阵为J=kg/m2。

跟随航天器相对于理想位置的初始位置矢量在跟随航天器本体坐标系中表示为，初始相对速度为[ 0.1 0.05 -0.2 ]Tm/s，初始相对姿态四元数为qBD(t0)=0.4618i+0.1917j+0.7999k+0.3320，初始相对角速度为外部扰动力和力矩分别为

滑模面参数设置为k1= 0.5+ε0.5，γ= 0.8，控制律参数设置为k2= 10 +ε20，k3= 0.001+ε0.001。

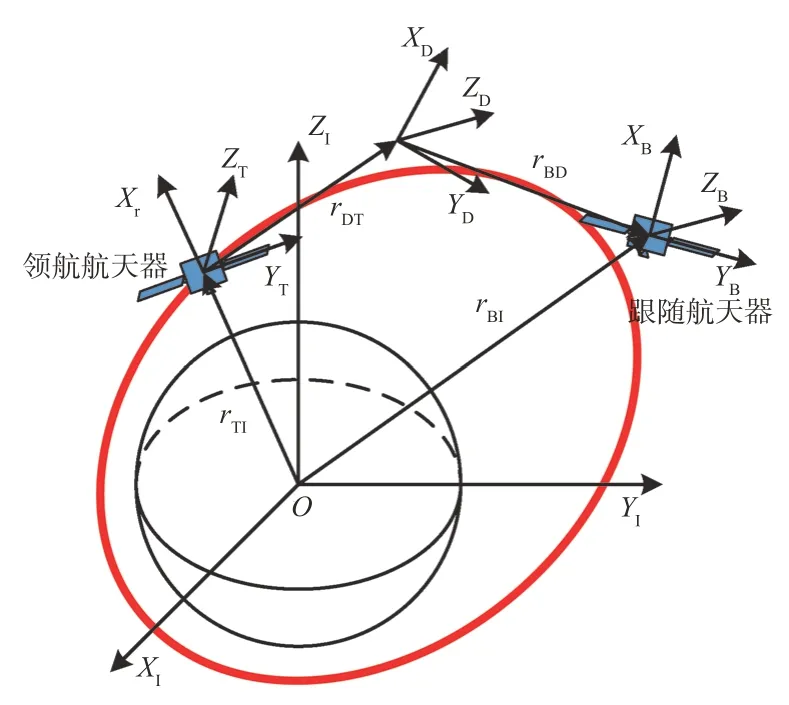
图2 领航坐标系、理想坐标系和跟随坐标系的关系Fig.2 Relation between leader frame,desired frame and follower frame

图3给出了跟随航天器相对于理想坐标系的相对位置变化曲线，可以看到相对位置的分量都较为平缓地收敛到了0 附近，意味着跟随航天器运动到了理想位置并保持在理想位置。图4 描述了对应的相对速度变化，从图中可以看出，相对速度分量的变化与对应的位置分量的变化一致，验证了twistor描述的相对运动的正确性。

图3 跟随航天器相对于理想坐标系的位置曲线Fig.3 Relative position profiles of the follower spacecraft with respect to the desired frame

图4 跟随航天器相对于理想坐标系的速度曲线Fig.4 Relative velocity profiles of the follower spacecraft with respect to the desired frame

跟随航天器相对于理想坐标系的twistor 变化曲线见图5，各个分量都精确收敛于零附近，表明跟随航天器的姿态与理想坐标系的姿态重合。图6描述了跟随航天器相对于理想坐标系的角速度变化，可以看到，为了较快地减小角度误差，角速度各个分量的大小先增大到较大值，然后再缓慢收敛到0附近。

图5 跟随航天器相对理想坐标系twistor变化曲线Fig.5 Twistor profiles of the follower spacecraft with respect to the desired frame

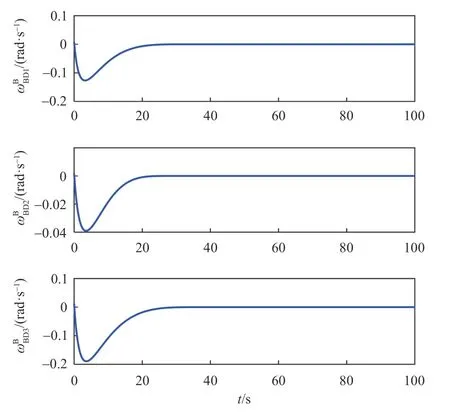
图6 跟随航天器相对于理想坐标系的角速度曲线Fig.6 Relative angular velocity profiles of the follower spacecraft with respect to the desired frame

图7和图8分别给出了控制力和控制力矩的变化曲线。显然，由于用sigmoid 函数代替了sign 函数，控制量并没有出现抖振现象，而且所需控制力和控制力矩都比较小，能够满足航天器动力系统的要求。

图7 控制力剖面Fig.7 Profiles of the control force

图8 控制力矩剖面Fig.8 Profiles of the control torque

5 结 论

本文针对航天器的六自由度领航-跟随编队控制问题，采用twistor 对航天器的六自由度运动进行描述，并基于此设计twistor 框架下的终端滑模控制律，实现扰动环境下航天器六自由度领航-跟随编队的精确控制。通过数值仿真，验证了所提出方法的正确性，并得到以下结论：

（1）基于twistor 的航天器六自由度姿轨耦合相对运动统一描述能够简化航天器六自由度相对运动控制律的设计，并且能够避免传统欧拉角描述姿态运动的奇异性问题。

（2）Twistor描述的航天器姿轨运动方程比对偶四元数描述的姿轨运动方程的维数低，计算量小，更适合计算资源有限的在线计算。

（3）Twistor 框架下的姿轨耦合终端滑模控制律，在扰动环境下能够在有限时间内同时使领航-跟随编队航天器的相对位置误差和相对姿态误差收敛到0附近。

（4）基于twistor 的姿轨耦合控制律的设计更为简洁，可以进一步推广到分布式多航天器编队飞行的六自由度控制，是后续研究的重要内容。