基于超螺旋干扰观测器的组合体航天器姿态接管控制

吕跃勇，秦堂皓，张 薇，方 慧

（1. 哈尔滨工业大学，哈尔滨150001；2. 上海航天控制技术研究所，上海201100）

1 引 言

随着人类对宇宙空间探索脚步的加快，空间中的航天器数量也在逐年增加，为了确保这些航天器顺利完成任务，航天器在轨服务技术应运而生。航天器在轨服务［1］（On-Orbit Servicing，OOS）是指通过人、机器人或两者协同来延长各种航天器寿命，提升其执行任务能力的一类空间操作。广义的空间在轨服务技术涵盖在轨装配、卫星回收、加注延寿、轨道转移、碎片清除以及空间攻防等多个领域，是航天领域的热点问题。国内外已经开展了许多在轨服务技术相关研究项目，例如欧空局的CXOLEV［2］太空拖船项目接管失效卫星。美国在SUMO/FREND［3］项目中提出了凤凰计划，旨在抓捕卫星后进行拆解再组装，具有明显的天基攻防军事化应用意图［4］。美国诺斯罗普·格鲁曼公司的MEV-1［5］与国际通讯卫星Intelsat-901 在地球静止轨道上空300 公里处的坟墓轨道上进行了对接。MEV-1 通过一种可以插入Intelsat-901 远地点发动机的机械捕获装置与其完成对接和组合，接管操控了Intelsat-901 的轨道和姿态运动，使这颗已在轨运行19年的卫星可以延长5年工作寿命。这是历史上首次在目标卫星上没有预先设计接口的前提下，对在轨运行的卫星进行捕获和对接。

完整的在轨服务过程大体可以分为四个阶段：远距离导引、近距离逼近、抓捕组合、接管操控［5］。服务航天器在捕获目标并与之构成组合体后，通过自身执行机构驱动组合体进行姿态或轨道运动，从而实现对目标的接管操控。由于目标航天器多为非合作目标，即目标航天器存在着服务航天器所未知的液体晃动、柔性结构振动、惯性特性、质量分布以及执行机构输出等不确定性，故所构成的组合体航天器也就存在着诸多不确定性，如质心位置未知、惯性矩阵未知、存在未知力矩输入以及外界未知力矩干扰等。因此组合体航天器的高精度、高性能以及高可靠的姿态控制是关键技术，具有十分重要的工程意义。

为了实现高精度的组合体航天器质量特性辨识，国内外的专家、学者提出了许多解决方案。刘超镇等［6］提出对角速度进行差分以得到角加速度，最后利用最小二乘方法对角速度和姿态等状态量进行结算，得到组合体航天器的转动惯量参数。王明等［7］提出利用服务航天器上附加的空间机械臂的运动来激励组合体航天器获得速度，再利用最小二乘算法进行结算来得到组合体航天器的质量特性参数。张海博等［8］提出利用喷气装置对组合体航天器产生力矩激励，借助加速度计对运动状态参数进行测量，最后利用最小二乘方法对组合体航天器质量特性进行结算。以上文献使用在轨辨识的方法获取组合体航天器的转动惯量等参数，方法直观且执行简便，但在轨辨识消耗服务航天器燃料，且受到外界的干扰力矩作用，所得参数的精度不高，为实现对组合体航天器的高精度控制，利用敏感器获取目标航天器状态，并通过服务航天器的执行器对组合体航天器进行控制。Bandyopadhyay等［9］提出了一种使用非线性跟踪控制器的方法，实现对大型物体（如小行星）的航天器姿态的稳定接管控制。文献［10］设计了一种基于神经网络技术的自适应姿态控制器；于欣欣等［11］提出利用基于模型的智能自适应控制方法对组合体航天器进行姿态控制；康国华等［12］借助深度学习方法，利用训练好的神经网络对组合体航天器的姿态进行控制。以上文献只是增加了对组合体航天器控制的鲁棒性，但在快速性以及抗扰性上有所欠缺。超螺旋干扰器能够对时变、有界但未知的干扰进行估计，并在有限时间内收敛，具有良好的快速性和鲁棒性。文献［13］设计了一种固定增益的超螺旋干扰观测器对组合体航天器进行姿态控制，但由于采用固定增益降低了观测器的灵活性，观测性能仍有进一步提升的空间。

综上，本文针对在轨服务航天器对非合作目标的姿态接管控制问题，围绕组合体航天器姿态动力学建模、控制与仿真，提出了一种自适应超螺旋干扰观测器作为前馈补偿的姿态接管控制方案，实现了对目标航天器的姿态接管。

2 组合体航天器姿态运动建模

本文以存在对抗性力矩的完全约束组合体航天器为研究对象，系统结构如图1所示。

图1 中OsXsYsZs是服务航天器的本体坐标系，OtXtYtZt是目标航天器的本体坐标系，ObXbYbZb是组合体航天器的本体坐标系，OiXiYiZi是地心惯性坐标系，Cs，Ct分别为从服务航天器本体坐标系及目标航天器本体坐标系到地心惯性坐标系的转换矩阵。Cst、C-1ts分别表示从目标航天器本体坐标系到服务航天器本体坐标系的转换矩阵及其反变换矩阵。通过分析服务航天器与目标航天器间通过空间机械臂传递的相互力矩方式，利用欧拉刚体方程建立服务航天器及目标航天器的姿态动力学模型，二者在组合体航天器本体坐标系内的姿态动力学模型可分别写作：

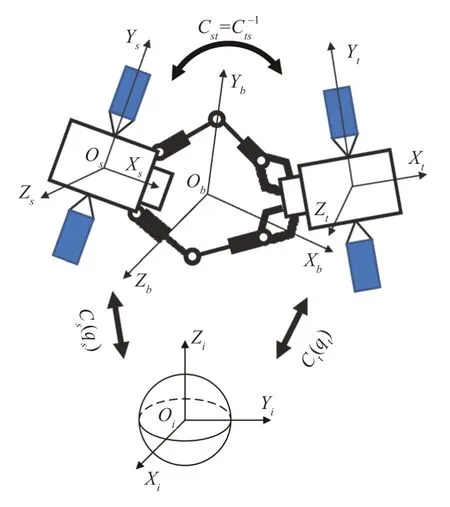
图1 组合体航天器坐标系及空间转换关系示意图Fig.1 Schematic diagram of combined spacecraft coordinate system and space conversion relationship

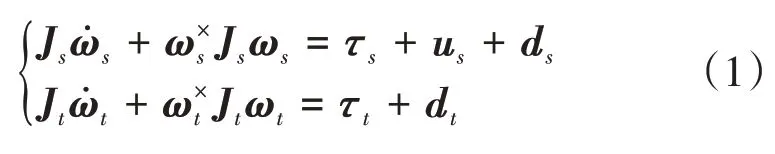
其中，Js，Jt∈R3×3分别为服务航天器及目标航天器的转动惯量矩阵，ωs，ωt∈R3×1分别为服务航天器及目标航天器相对于地心惯性坐标系的姿态角速度在各自本体坐标系中的投影，us∈R3×1为服务航天器输出的控制力矩，ds，dt∈R3×1分别为服务航天器及目标航天器受到的外界干扰力矩，τs，τt∈R3×1分别为服务航天器与目标航天器受到的来自对方的相互作用力矩，其中ω×为向量ω的反对称矩阵，对于任一向量ω=[ω1ω2ω3]T∈R3的矩阵叉乘计算可简化为ω×Jω≜ω×Jω，ω×定义为：

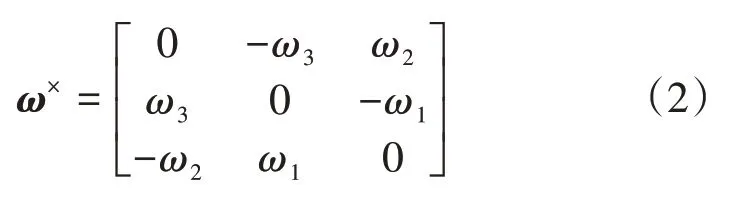
由于本文只考虑服务航天器与目标航天器之间存在完全约束，因此服务航天器的本体坐标系与目标航天器的本体坐标系之间存在着常数转换矩阵，而二者间的相互作用力矩τs，τt和姿态角速度变量ωs，ωt等参数均可以通过旋转矩阵相互转换：

其中，Cst∈R3×3表示从目标航天器本体坐标系到服务航天器本体坐标系的转换矩阵。其求取方法如下：

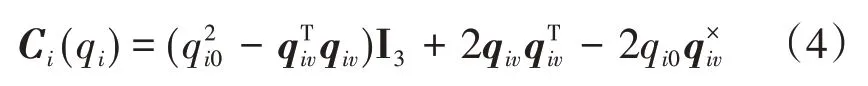
则可求得目标航天器本体坐标系与服务航天器本体坐标系互相转换的矩阵为：

综上所述，结合式（1），式（3）及式（5），可推导出服务航天器与目标航天器间的相互作用力矩τs的表达式：

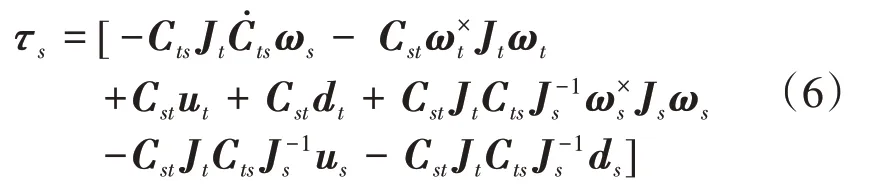
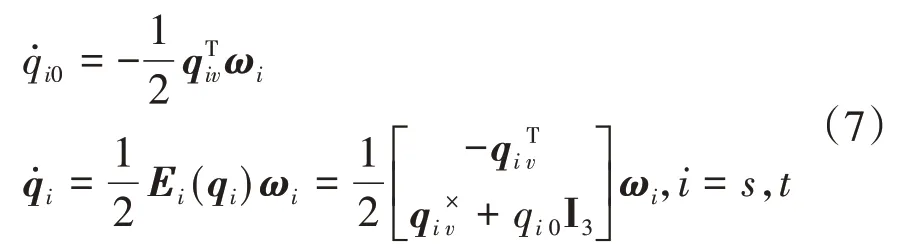
至此，本文可用式（1），式（6）及式（7）共同描述组合体航天器的姿态。

3 基于超螺旋干扰观测器的组合体航天器姿态控制

3.1 前馈补偿控制方案设计

由于控制器及执行机构均位于服务航天器，以服务航天器为基准，结合上文的组合体航天器姿态模型式（1），组合体航天器姿态方程可写作：

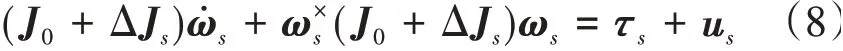
其中，J0为服务航天器绕自身惯性主轴的惯性矩阵，ΔJs是服务航天器质心位置发生变化而产生的转动惯量偏差。

由于目标航天器的质量特征参数未知且可能存在对抗性姿态机动，ΔJs无法准确获知。τs作为内部相互作用力矩不可直接测量。上述因素为服务航天器接管目标姿态带来了挑战，传统基于模型或在轨辨识的方法不再适用。可将目标航天器通过机械臂传递到服务航天器的反作用力矩视为作用在服务航天器本身的广义干扰力矩，该力矩的方向、大小与接管操控策略、目标特性、对抗强度均有关，属于典型的上界未知、时变干扰力矩。因此，本文针对广义干扰力矩的时变未知特性，提出一种基于超螺旋干扰观测器的前馈补偿姿态接管控制方案。对于内部作用力矩τs与其他干扰因素共同构成的广义干扰力矩，采用超螺旋干扰观测器进行实时观测。

超螺旋算法是典型的二阶滑模算法，可写作形式［14］：

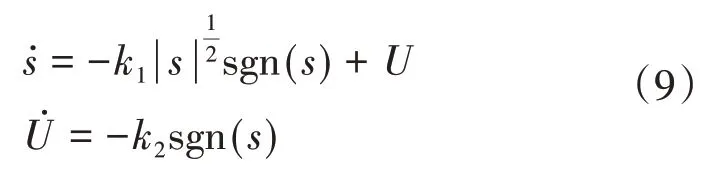
其中，s为滑模变量，ki为待设计的常数增益，U为中间 变 量。令x2=ωs，则本文的服务航天器的姿态动力学及运动学模型状态空间形式写作：

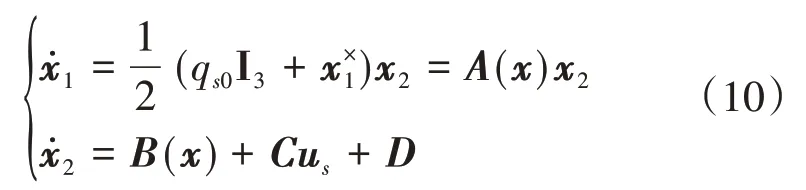
若用表示系统状态x2的观测值，则根据服务航天器的姿态动力学方程的状态空间表达式，有下式成立：

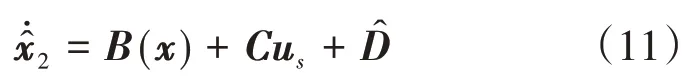
则系统状态x2的观测误差可写作：

参考式（9），可将超螺旋干扰观测器设计为如下形式：

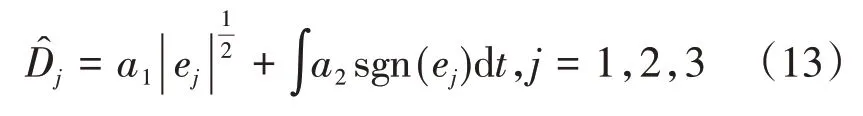
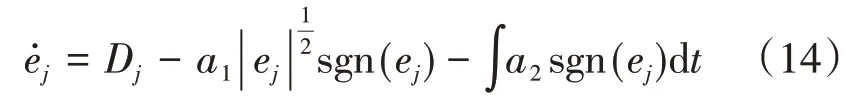
从式（13）可以看出超螺旋算法具有有限时间收敛［10］、不需要滑模变量导数等优点，可以实现对广义干扰的快速观测，从而提升系统控制性能。

根据前馈补偿原理，将超螺旋干扰观测器的观测值作为前馈补偿项，结合PD控制器，设计的组合体航天器姿态控制律形式如下：

其中，Kp为比例系数，Kd为微分系数。根据临界比例度法，可使PD 控制部分usPD=-Kpqsv-Kdωs收敛。在式（13）中设计的超螺旋干扰观测器中，增益a1，j，a2，j为常值，为实现对非合作目标产生的非周期性、幅值变化大的广义干扰更好的观测效果，引入自适应算法，将增益a1，j，a2，j设计成与当前观测误差ej有关的自适应增益，以期提高干扰观测的精度及效率，下文进行自适应超螺旋干扰观测器设计。

3.2 自适应超螺旋干扰观测器设计

引入自适应算法后可将超螺旋干扰观测器设计为如下形式：

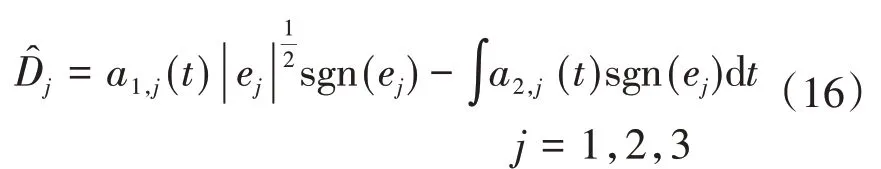
其中，a1，j(t)和a2，j(t)为自适应增益，

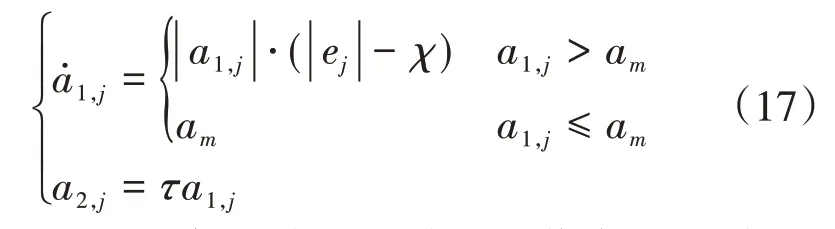
其中，τ，χ，am为待设计的正常数，若存在正常数ρ，λ使得式（18）成立，则观测误差ej，j= 1，2，3 可以在有限时间内收敛。

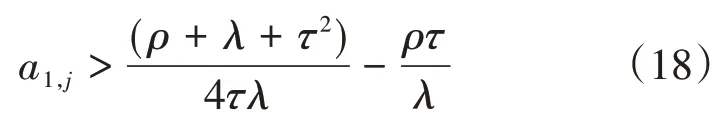
假设存在两个中间变量M∈R3×1，N∈R3×1，其形式如下式所示。

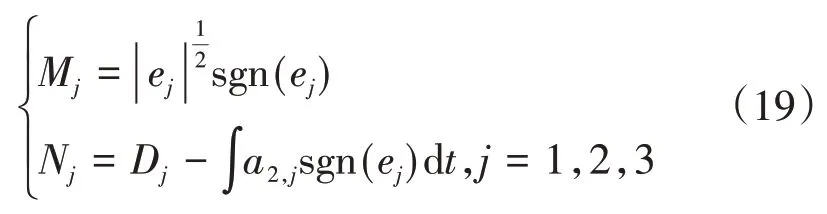
设ξj=[Mj Nj]T，并对其进行求导有：

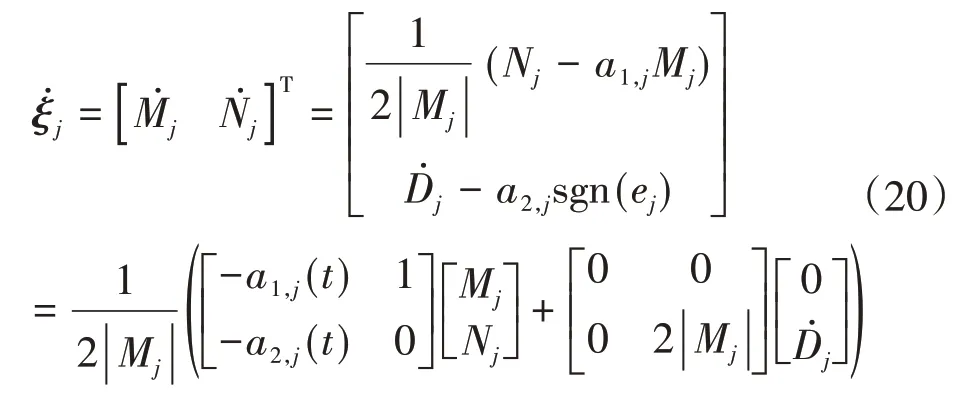
假设总干扰D及其一阶导数̇均有界，即满足，假设存在常数ρ满足0 ＜ρ＜2Δ2，则可将写作如下形式：

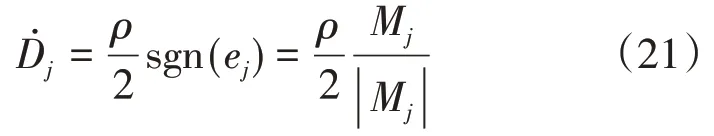
将式（21）代入式（20）并进行整理可得：

设计Lyapunov函数如下：

其中，P为对称正定矩阵，且

将式（23）的Lyapunov函数对时间求导有：

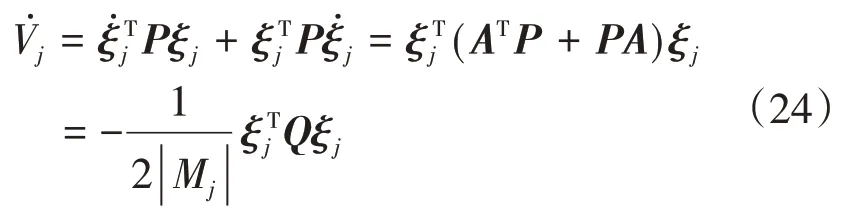
最小特征值满足λmin(Q)≥τ，a1，j＞

则有：

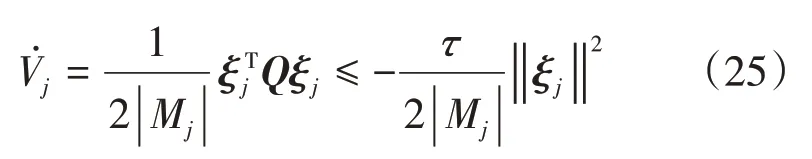
对于式（23）有下式成立：

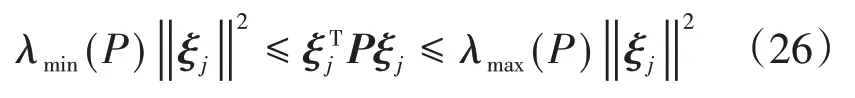
对式（25）和式（26）整理可得

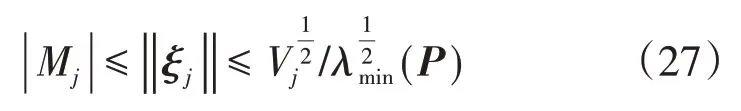
综上可得：

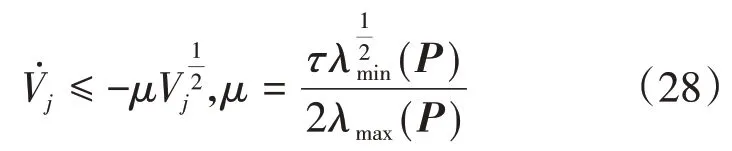
式（28）满足文献［15］中引理1 给出的系统在有限时间内稳定的条件，因此式（13）所设计的超螺旋干扰观测器可以在有限时间内收敛，但式（28）只证明了超螺旋干扰观测器观测误差收敛，为证明自适应超螺旋干扰观测器稳定，在此设计另一个Lyapunov函数：

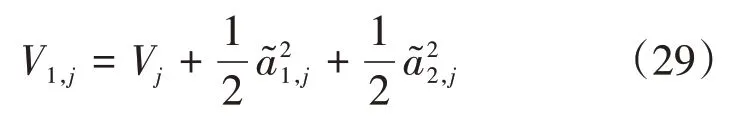
对式（29）的Lyapunov函数进行求导有：

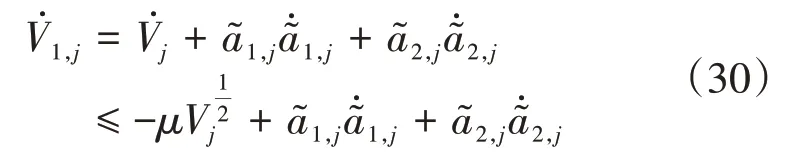
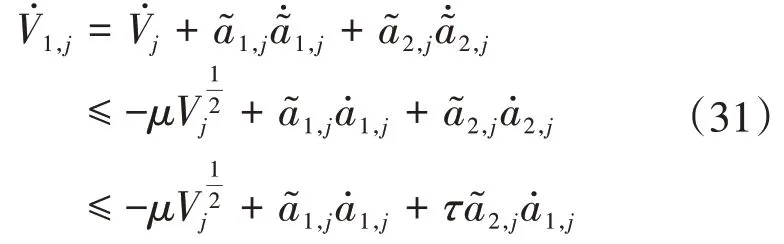
选取两个辅助常数l1，l2，需满足如下约束：

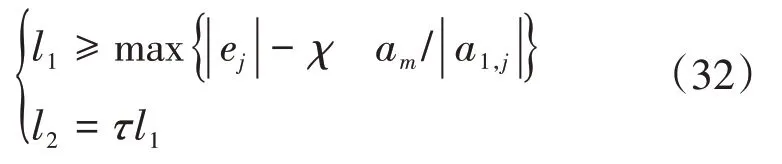
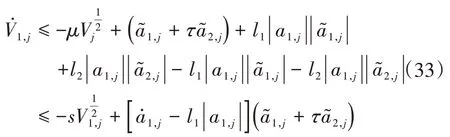
根据文献［15］的定理1，当a1，j＞am以及a1，j≤am时分别存在：

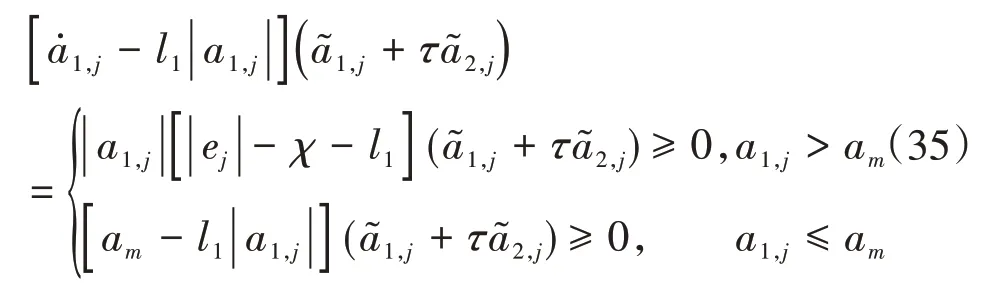
综上可得：

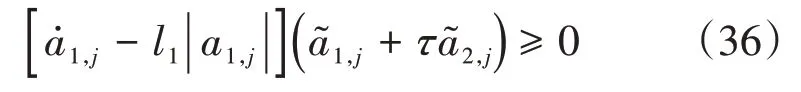
因此，根据文献［15］的引理1 可以看出状态观测误差e以及干扰观测误差D͂均可以在有限时间内收敛，即上述设计的自适应超螺旋干扰观测器是在有限时间内稳定的。

4 数值仿真

本节通过数值仿真验证了基于超螺旋观测器的控制方法的有效性，在组合体航天器坐标系下，航天器质量特性如表1 所示，控制器参数如表2 所示。服务航天器期望四元数和期望角速度分别为qsd=[1 0 0 0]T和ωsd=[0 0 0]Trad/s，初始四元数和初始角速度分别为ωs0=[0.1 0.1 0.1]Trad/s，qs0=[0.3 0.4 0.5 0.707]T。

表1 航天器质量特性Table 1 Spacecraft mass and inertia property

表2 控制器参数Table 2 Controller parameters

由于仅有服务航天器上安装有敏感器，故在接下来的仿真过程中，仿真结果均为服务航天器的参数变化曲线。服务航天器的姿态角速度、姿态四元数以及控制力矩的变化曲线分别如图2～4所示。

图2～4 的仿真结果表明，基于前馈补偿的PD控制器可以实现对组合体航天器姿态快速、平稳的接管操控。超螺旋干扰观测器自适应增益变化曲线如图5 所示，超螺旋干扰观测器对系统广义干扰的跟踪曲线如图6所示。

从图5 可以看出，超螺旋干扰观测器可以跟随干扰变化动态调整增益，提升系统的鲁棒性。从图6 可以看出，超螺旋干扰观测器可以快速对广义干扰进行准确估计，提高了系统控制效果。上述仿真结果表明，基于超螺旋干扰观测器前馈补偿项的PD 控制器可以快速、精准地对组合体航天器姿态进行控制，为组合体航天器姿态接管控制提供了一种解决思路。

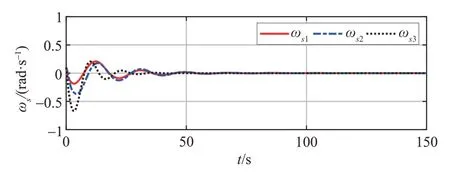
图2 服务航天器姿态角速度变化曲线Fig.2 Service spacecraft attitude angular velocity change curve

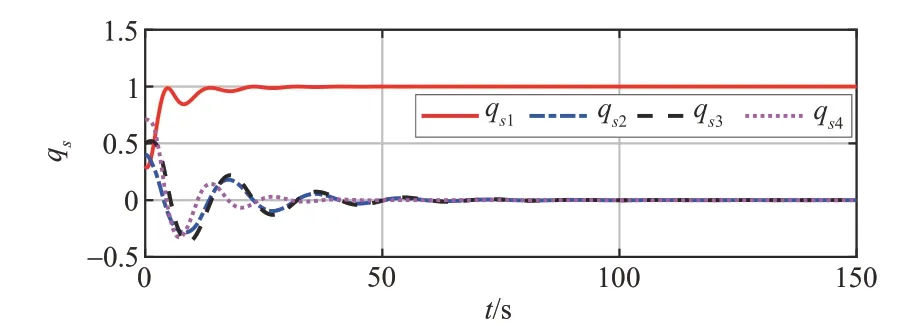
图3 服务航天器姿态四元数变化曲线Fig.3 Service spacecraft attitude quaternion change curve

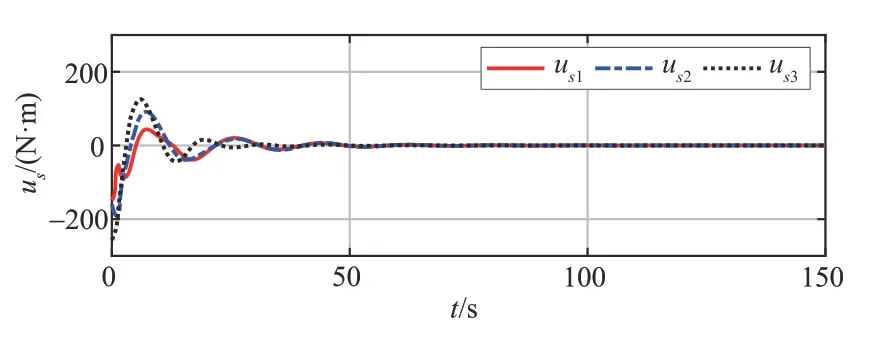
图4 服务航天器控制力矩变化曲线Fig.4 Service spacecraft control torque change curve

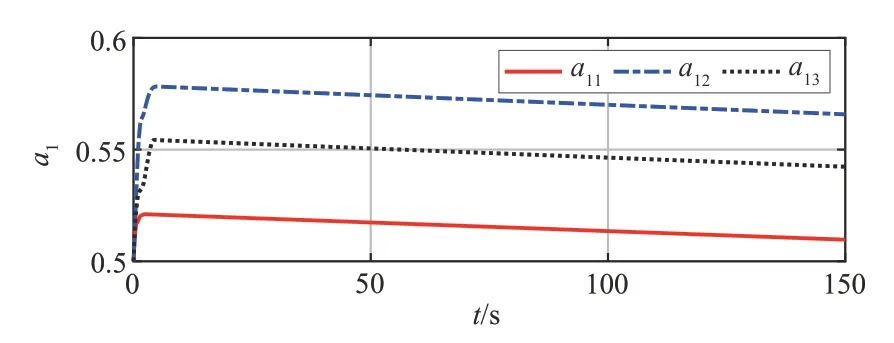
图5 超螺旋干扰观测器自适应增益变化曲线Fig.5 Adaptive gain curve of super-twisting interference observer

5 结 论

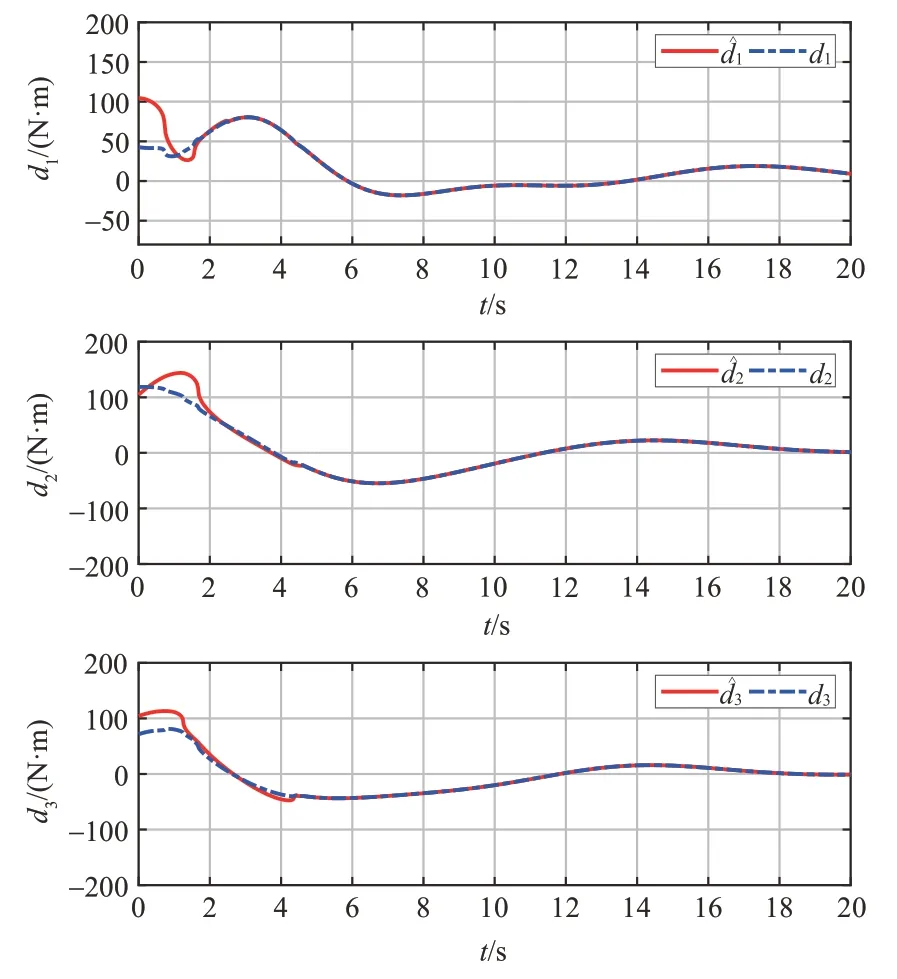
图6 超螺旋干扰观测器对系统等价干扰的跟踪曲线Fig.6 Tracking curve of super-twisting interference observer to system equivalent interference

本文针对非合作目标的姿态接管控制问题，基于状态一致性原则建立了不依赖于目标参数的组合体航天器姿态运动数值仿真模型，提出了一种基于超螺旋干扰观测器的前馈补偿姿态接管控制方案，基于Lyapunov稳定性理论分析了所提出的自适应超螺旋干扰观测器的有限时间收敛特性，同时数值仿真结果也进一步验证了本文所提出的组合体姿态接管控制方案的有效性，得出了以下主要结论：

（1）基于状态一致性原则构建的组合体航天器姿态运动数值仿真模型能够准确的描述组合体的姿态运动，且形式相对简单。

（2）所提出的自适应超螺旋干扰观测器能够快速、准确、实时估计目标引起的服务航天器广义干扰力矩，其观测值作为前馈补偿项，有效提高了PD控制器的接管作用效果。