基于网格编码差分进化的在轨服务星群任务规划方法

史人赫，宝音贺西，龙 腾，魏 钊

（1. 清华大学航天航空学院，北京100084；2. 北京理工大学宇航学院，北京100081；3. 飞行器动力学与控制教育部重点实验室，北京100081）

1 引 言

为了保证空间系统在恶劣的空间环境中能够长期稳定的在轨运行，在轨服务应运而生。在轨服务是指人或者服务航天器针对空间系统进行的各类空间操作［1］，主要包括在轨装配、在轨监测、在轨维护、空间碎片清理等［2］。在轨服务为空间任务的实施提供了更多选择，具有延长在轨系统寿命、提升任务执行能力、降低初始成本、增强在轨灵活性和适应性等重要意义［3］。目前，以美国为首的发达国家高度重视在轨服务技术的发展，开展了轨道快车、凤凰等在轨服务技术验证计划［4-5］。作为在轨服务任务实施的前端和顶层，在轨服务任务规划主要通过求解多空间目标交会问题，在满足各类复杂约束条件下，确定服务航天器对目标航天器的轨道转移与交会方案，使得在轨服务任务效益最大化［6］。如何有效求解复杂在轨服务任务规划问题，成为了国内外研究热点。

按照在轨服务任务的不同，在轨服务通常可以分为一对一、一对多、多对一和多对多等不同模式。目前，国内外围绕不同模式下的在轨服务任务规划技术开展了广泛研究。例如，文献［6］围绕不同任务场景下的在轨服务任务规划模型开展了系统研究；Yu等［7］考虑服务窗口、末端状态、时间分配等约束，以总速度增量最小为目标，建立了离散连续混合的空间碎片主动清除任务规划模型，并通过定制的粒子群优化算法对任务规划问题进行了求解；Yang 等［8］建立了考虑最大回报值的多空间碎片主动清理预先任务规划模型，提出了一种贪婪启发式算法，实现了该问题的高效求解；Madakat 等［9］针对LEO 空间碎片清理问题建立了双目标的旅行商问题模型，并通过分支定界方法完成了求解；梁彦刚等［10］采用多目标遗传算法求解在轨服务航天器任务指派问题，获取了速度增量-变轨时间的Pareto前沿；Baranov［11］等人针对地球静止轨道空间碎片清理任务规划问题，为服务航天器设计了两阶段的最优轨道转移方案。

为了进一步提高在轨服务任务规划求解效率，本文以共面圆轨道卫星星群一对一在轨服务问题为对象，开展基于网格编码差分进化的在轨服务任务规划方法研究，在两层任务规划框架的基础上，通过定制一种新型网格编码生成技术与差分变异操作机制，实现共面圆轨道卫星星群一对一在轨服务规划问题的有效求解。

2 在轨服务任务规划模型

2.1 一对一在轨服务任务规划框架

本文研究的在轨服务任务规划问题采用一对一工作模式，即一颗服务星对一颗目标星进行服务，且服务卫星星群和目标卫星星群位于共面圆轨道，各目标星的优先级相同。为了实现在轨服务任务规划问题的高效求解，本文构建了如图1 所示的两层任务规划框架。其中，任务分配层通过定制的网络编码差分进化算法，生成满足一对一约束的服务星任务指派方案；规划求解层中，服务星群按照任务分配结果通过双脉冲霍曼转移实现和对应目标星的空间交会，并计算轨道转移时间、速度增量等指标作为任务规划目标函数；最终根据优化收敛条件，判断任务规划求解过程是否终止。

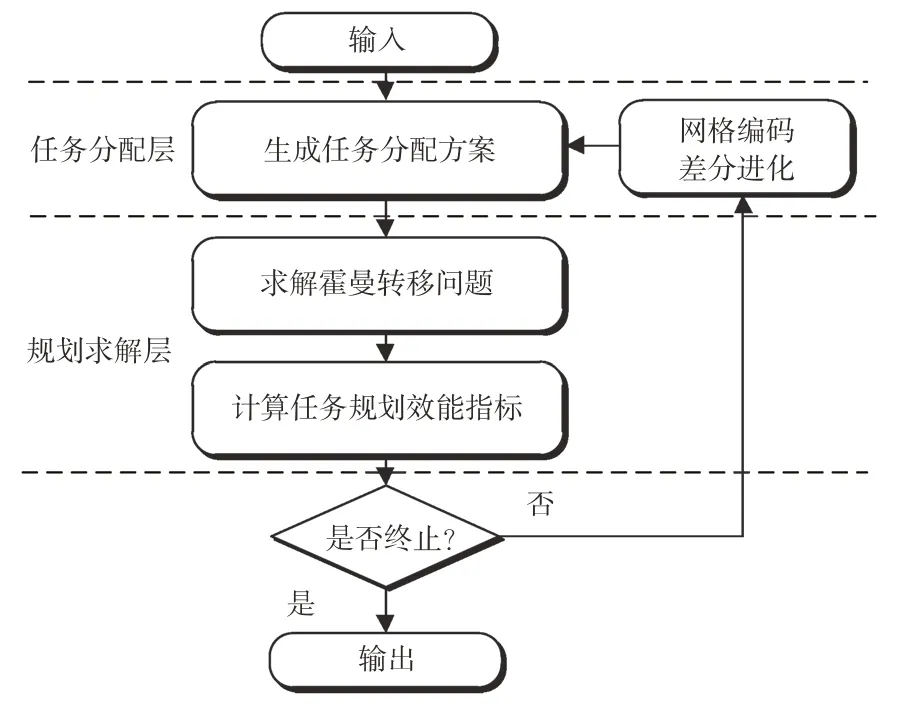
图1 在轨服务任务规划框架Fig.1 On-orbit servicing mission planning framework

基于上述在轨服务任务规划框架，建立如式（1）所示的一对一在轨服务任务规划优化问题的数学模型：

其中，X为指派变量矩阵，其元素xij=1 时表示第i个服务星对第j个目标星进行服务，xij=0 表示不存在服务关系；ti和Δvi分别为第i个服务星轨道转移时间与变轨所需速度增量，由空间交会模型计算得到；w1和w2分别为在轨服务任务时间和能量指标的加权系数；t0和v0为归一化因子，用以消除不同指标量级造成的差别；约束条件g1表示每个目标星必须且只能接受一个服务星；约束条件g2表示每个服务星最多服务一个目标星。

2.2 双脉冲霍曼转移模型

本节对在轨服务任务规划框架采用的双脉冲霍曼转移模型进行简要介绍。双脉冲霍曼转移过程如图2 所示，服务星在轨道半径为r1的圆轨道C1的任意点P 处产生第一个速度增量Δv1，进入椭圆转移轨道E，并在E 的远地点A 产生第二个速度增量Δv2，进入半径为r2的圆轨道C2。

图2 霍曼转移过程示意图Fig.2 Illustration of Hohmann transfer

霍曼转移过程两次脉冲所需的速度增量如式（2）所示：

其中，vC1和vC2分别为半径r1和r2圆轨道的速度。对应的霍曼转移变轨时间为：

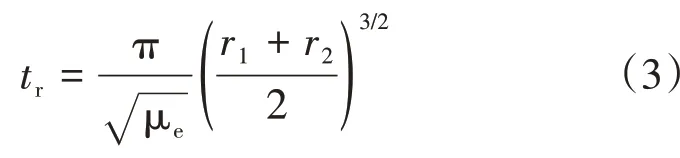
其中，μe= 398600.5 km3/s2为地球常数。

此外，为了实现服务星与目标星的交会，在轨道转移前目标星需要超前服务星一个提前角θH，因此服务星需要根据和目标星的相对相位在停泊轨道上等待一段时间。因此，服务星的实际轨道转移时间为等待时间和变轨时间之和。文献［12］中给出了双脉冲霍曼转移时间和速度增量的详细计算方法。

3 网格编码差分进化算法

3.1 总体流程

为了高效求解式（1）中的在轨服务任务规划问题，本研究在标准差分进化算法的基础上［13］，提出了一种网格编码差分进化算法（Grid Coding based Differential Evolution，GCDE）。该方法通过一种随机序列逐次枚举的指派矩阵生成算法，保证每一代个体自动满足规划约束条件，并通过定制网格编码差分变异操作，实现设计空间的高效探索。GCDE的具体步骤叙述如下。

步骤1：初始化。利用NP个维度为n×m的0-1任务指派矩阵作为每一代的种群Pk，G，种群中的每个个体（即任务指派矩阵）表示为：

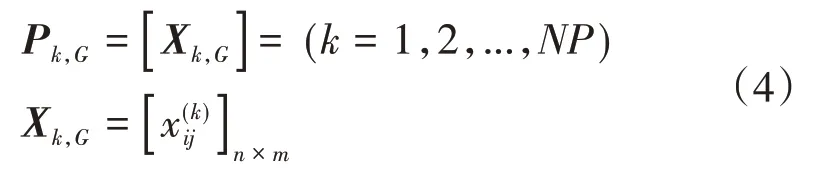
其中，k为个体编号，G为进化的代数，Xk，G分别为第k个个体对应的任务指派矩阵。3.2 节中给出了Xk，G的具体生成方式。

步骤2：网格编码差分变异。为了产生变异向量，算法从当前种群中随机选择三个个体Xr1，G，Xr2，G，Xr3，G，在此基础上，采用式（5）所示的差分变异方法产生变异向量。

式（5）中，vk，G为受体向量，⊕和⊗为网格编码差分变异操作算子。其中，⊗表示广义差分运算，用于计算Xr2，G和Xr3，G的差异性；⊕为广义变异运算，用于根据差分结果实现Xr1，G的扰动。3.3 节中给出了网格编码差分变异操作的详细介绍。

步骤3：选择。按照式（6）进行选择，确定vk，G是否作为下一代的个体成员。若vk，G的任务规划目标函数值不劣于当前个体Xk，G，则将其替代Xk，G作为新的种群个体参与下一轮迭代；反之则不会保留vk，G。

步骤4：对当前种群中的每一个个体重复上述优化过程，直至达到模型最大调用次数或最大进化代数，最终输出最优任务规划结果。

3.2 基于序列逐次枚举的网格编码方法

为了减少计算成本，保证任务规划结果的可行性，本研究引入随机序列逐次枚举思想［14］，实现Xk，G的快速可靠生成。图3中给出了Xk，G生成过程的示意图，具体步骤包括：

步骤1：生成n×m的二维平面网格，令网格列编号q=1，可用行编号r=[1，2，...，n]。

步骤2：在第q列网格中，随机从r中选取一个元素r(t)，为坐标为[r(t)，q]的网格赋值为1，为当前列其他网格赋值为0，并从r中删除r(t)。

步骤3：若q≠m，则q=q+1 返回步骤1.1；否则算法终止，输出指派矩阵个体Xk，G。

可以看出，按照上述方法生成的任务指派矩阵自动满足在轨服务任务规划问题中的一对一约束条件，且交换任务指派矩阵网格编码中任意两列或两行，不改变任务规划结果的可行性，从而有效提升了在轨服务任务规划约束优化问题的求解效率和鲁棒性。

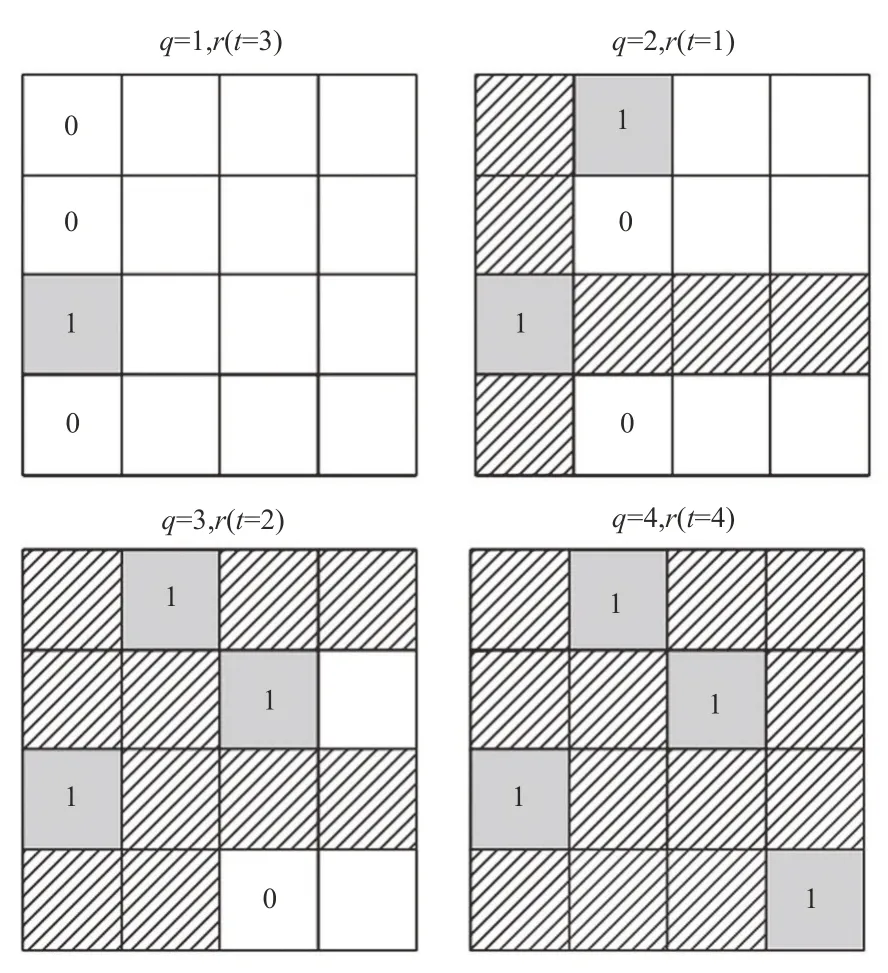
图3 网格编码生成过程示意图Fig.3 Illustration of grid coding generation

3.3 网格编码差分变异操作

作为差分进化算法的核心，差分变异通过寻找两个随机个体之间的差别对目标个体进行扰动，从而实现设计空间探索［15］。与传统连续优化问题或者二进制离散编码形式不同，GCDE 采用平面二维网格编码方式构建子代个体，因此无法直接通过传统差分操作产生变异个体向量。因此，本研究根据网格编码交换任意两列不破坏一对一任务约束的特点，定制了一种新型网格编码差分变异操作，其示意图如图4所示，具体步骤叙述如下。

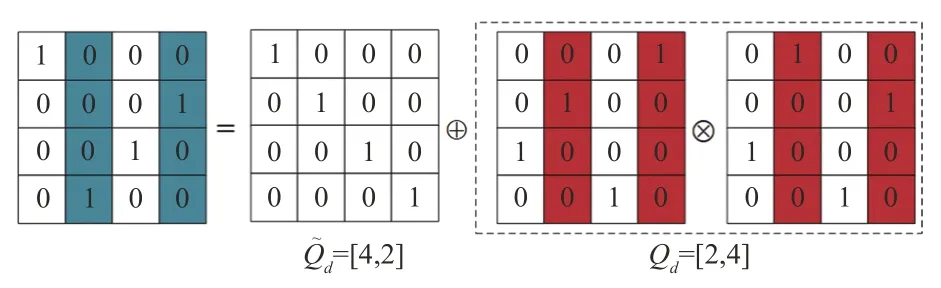
图4 网格编码差分变异操作示意图Fig.4 Illustration of grid coding differential mutation operation

步骤1：对于随机选择的个体Xr2，G和Xr3，G，分别比较其网格编码，找到任务分配结果不同的列并记录为集合：

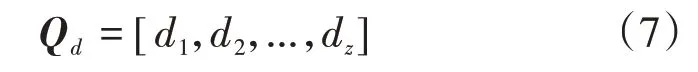
其中，dz为Xr2，G和Xr3，G中第z个不同编码列在网格编码矩阵中的索引序号。

步骤2：生成0～1 之间的随机数rand[0，1]，并与差分变异因子F进行比较。若rand[0，1]≤F，则将Qd中的索引序号顺序随机排列，重新生成一组索引F越大则表示当前个体具有更大的概率实现差分变异。

步骤3：在Xr1，G中，根据原始索引Qd找到对应的需要变异的列，并根据新的索引向量Q͂d交换列的顺序，生成变异后的受体向量vi，G。

4 工程案例

本节通过某卫星星群一对一在轨服务任务规划案例，对本文提出的GCDE方法的有效性和实用性进行验证。本案例中，12颗服务星均匀分布在半长轴为8378.14 km、轨道倾角为60°的圆形轨道上，8颗目标星均匀分布在同一平面内半长轴为8678.14 km的圆形轨道上，其初始轨道根数如表1 所示。采用GCDE 方法求解本案例中的在轨服务任务规划问题。其中，时间和能量指标的加权系数w1和w2均取0.5，归一化因子取t0=2592000 s 和v0=1000 m/s，GCDE 种群规模为96，最大进化代数为10，差分变异因子F=0.8，得到优化后的任务规划结果如表2所示。

从结果中可以看出，服务星群总体上优先选择轨道运行方向上相位差最小的临近目标星进行服务，从而同时降低在轨服务任务完成时间和燃料消耗。此外，优化后的任务规划方案满足一对一在轨服务模式下的任务指派约束，且所需的最大速度增量为122.0 m/s、最长变轨时间为40225.0 s，符合工程实际要求。为了进一步说明GCDE 的优化性能，本研究还采用MATLAB 提供的整数编码遗传算法（GA）工具箱求解上述在轨服务任务规划问题（GA种群规模为100，最大进化代数为100，其它参数采用MATLAB GA 工具箱默认设置），得到GCDE 与GA 优化结果对比如表3所示。表3中的结果表明，本文提出的GCDE 方法在求解卫星星群一对一在轨服务任务规划问题时具有更好的全局收敛性，且其计算成本相比于传统GA 减少了约90%，从而验证了GCDE的有效性和实用性。

表1 服务星和目标星初始轨道根数Table 1 Initial orbital elements of the service satellites and target satellites

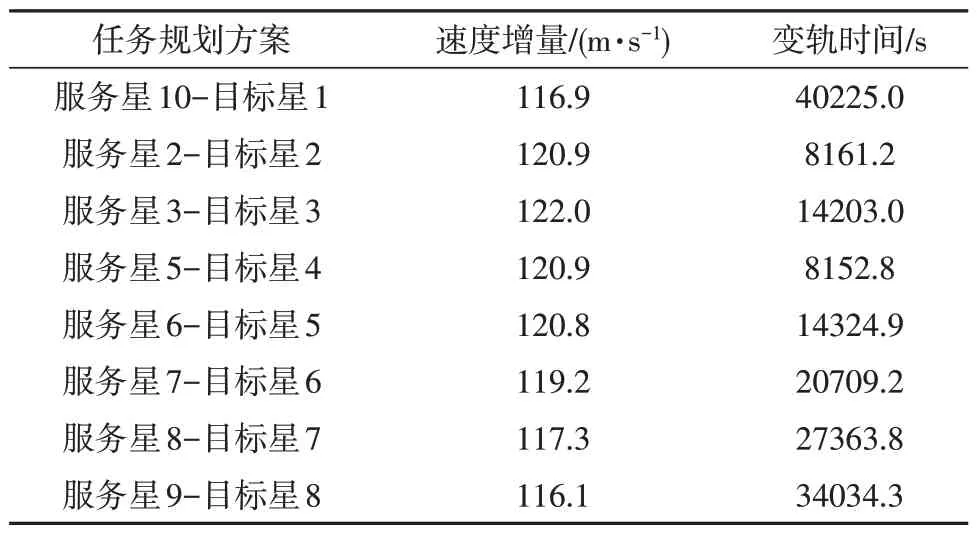
表2 任务规划结果Table 2 Results of mission planning

表3 GCDE和GA优化结果对比Table 3 Comparison of GCDE and GA optimization results

5 结 论

本文提出了一种基于网格编码差分进化的在轨服务任务规划方法，能够实现共面圆轨道卫星星群一对一任务规划问题的有效求解。本研究采用任务分配-霍曼转移两层结构建立了规划框架，并提出了一种新型网格编码差分进化算法，通过定制网格编码机制与差分变异操作，实现最优可行任务规划方案的高效求解。仿真案例表明，本文提出的网格编码差分进化方法能够实现共面圆轨道卫星星群一对一在轨服务任务规划问题的有效求解，且计算效率较传统遗传算法具有显著提升，从而验证了本文研究工作的有效性与工程实用性。