“学思课堂”模式下章末复习课的教学研究

李兰 顾大权

[摘  要] 章末复习课是指结束一章的教学内容后进行的复习课.“学思课堂”模式下的章末复习课不仅要巩固、梳理已学知识、技能、数学思想和方法，帮助学生提高解决问题的能力，形成良好的认知结构，使知识系统化，更要遵循“学思课堂”的模式，发挥“学思课堂”的特点，突出学和思，引导学生思考，在思考的过程中促进思维的发展.

[关键词] 学思课堂;章起始课;实践研究

“学思课堂”的基本模式

“学思课堂”主张“温故、知新、学思、笃行”，源于我国伟大的教育家孔子.“学思课堂”与传统的课堂教学相比，倡导“学”和“思”，出自《论语·为政》的“学而不思则罔，思而不学则殆”.“学思课堂”教学以“学”为主体，“思”为主线，“思”贯穿于“学”的整个过程，通过思考来启迪学生的思维，生成智慧. “学”是“思”的基础，“思”是“学”的升华，“学”与“思”交融，形成了一个积极的循环系统，会将所学的知识进行归纳整理，重新建构，把复杂的知识系统化、结构化，从而把握知识的核心.“温故、知新、笃行、学思”是“学思课堂”的四个教学环节. 温故：“故”是学生已有的知识和经验，“故”的设计要符合学生的认知规律和最近发展区，“故”的设计要考虑知识产生的背景和价值、知识形成的来龙去脉、知识的发展趋势，适合知新环节的探究学习.知新：在温故的基础上经历观察、猜想、交流、验证等学习活动生成新知，要让学生掌握研究數学问题的思路和方法，积累数学研究的活动经验.笃行：在知新的基础上，通过巩固强化来理解新知识，巩固新知识，例题、习题的设计要有典型性、针对性，有利于强化新知的理解和掌握. 学思：一是总结提升，思考新知所处的知识结构体系，将零散、孤立的知识点连成链、结成网，从整体的角度去建构新知.二是要将“思”贯穿课堂教学的每个环节，在各个环节中要思联结、思方法、思策略.

章末复习课的认识

数学复习课是一种常见的课型，是数学课堂教学的重要组成部分.复习课的种类很多，从范围上看有章末复习课、学期复习课和中考复习课，本文主要研究的是章末复习课.现行数学教材的编排是将整体的知识按教学内容的紧密安排各个章节，每一章都是一个整体，一章中的学习主题有多个，其间通常是以一节课为单位展开的;一节课又分为一个或几个知识点，按知识点进行教学的. 这样的编排遵循了学生的认知规律，分散了难点，但也会对知识的连续性、整体性造成破坏，知识点背后知识的整体结构关系不容易被发现，难以把握知识之间的内在联系.因此章末复习课应该起到巩固整理整章所学知识，完善整体的认知结构，提高综合运用能力的作用.“学思课堂”章末复习课的教学就是要遵循学思课堂的教学模式，发挥“学”与“思”融合的特征，在章末复习课中挖掘知识的内在联系，引发思考，拓宽思维的深度和广度，促进整体思维结构的形成，提升数学思维能力的发展.

“学思课堂”章末复习课的实践

章末复习课是对整章内容进行一次系统、全面的回顾与梳理，是对内容中知识技能、经验方法的升华，应对章节中的核心内容进行筛选、开发，通过对旧知的复习产生新的认识，实现温故知新的目的，同时也可以深化对知识的进一步理解和掌握，形成整体的思维结构，促进知识结构的迁移.下面以反比例函数章末复习为例，谈谈几点思考.

1. 温故：确定开放式起点，拓宽思维的广度

【教学片段1】

问题1：如图1所示，已知点A（2，3）在反比例函数的图像上，你能从图中得到哪些结论？

生1：可以求得反比例函数的关系式是y=.

师：方法是什么？

生1：待定系数法，设y=，将点A（2，3）代入求得k，从而求得关系式.

生2：可以知道k>0.

生3：可以看到图像在一、三象限.

师：还有吗？

生4：图像的形状是双曲线.

生5：性质是k>0时，在每个象限内， y随x的增大而减小.

思考：刚才回顾了哪些主要的知识点.

总结：

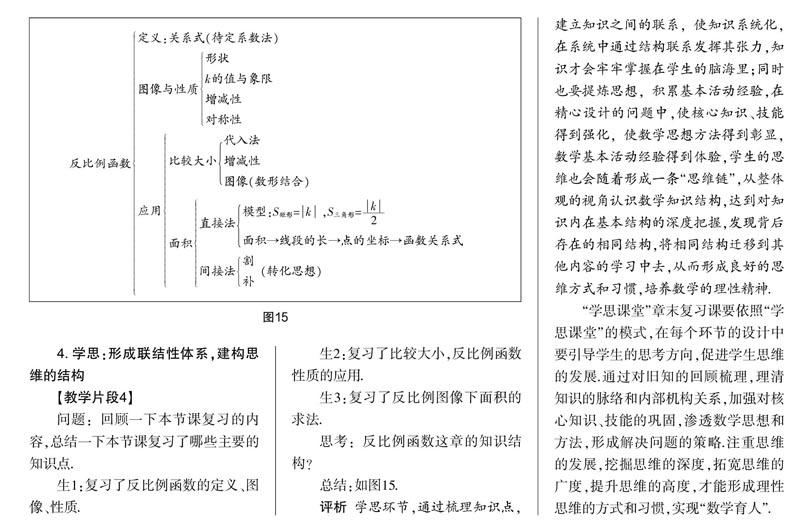
反比例函数关系式（待定系数法）图像与性质形状k的值与象限增减性？摇

评析  从一个图像的问题出发设计一个开放性问题，将反比例函数整章的核心知识——图像与性质进行了梳理，对关键技能——待定系数法也进行了回顾.温故环节的设计不再是已有知识点的简单重复，而是让学生对所学知识进行了多维度的回顾和整理，不但激发了学生的学习兴趣，而且还促进了学生的思维发展，拓宽了思维的广度.

2. 知新：设计递进性问题，挖掘思维的深度

【教学片段2】

问题1：如图1所示，已知点A（2，3）在反比例函数的图像上，在图像上取两点B（3，m），C（6，n），试比较m， n的大小关系.

生1：将B（3，m），C（6，n）两点代入y=，可以求得m=2， n=1，则m> n.

生2：可以根据性质：在第一象限内，由3<6，可得m> n.

生3：还可以根据图像：如图2，从图像上可以看出m> n.

师：这类问题可以采用代入求值法、函数的增减性和图像法去解决.

问题2：如图1所示，已知点A（2，3）在反比例函数的图像上，在图像上任取两点B（x1，y1），C（x2，y2），且x1

生4：B，C两点在第三象限，y随x的增大而减小.可由 x1

生5：还可以根据图像：如图3，从图像上可以看出y1>y2 .

生6：取特殊值，x1，=-2，x2 =-1，也可以比较出y1>y2 .

思考：解决这类问题的方法有哪些？

总结：（1）代入法（特殊值）;（2）反比例函数的增减性;（3）图像法（数形结合）.

问题3：如图1所示，已知点A（2，3）在反比例函数的图像上，在图像上任取两点B（x1，y1），C（x2，y2），且x1

（过程略）

总结：两点的位置不明确时需要分类讨论.

评析  学习是一个递进的过程，课时的教学可能由于时间等因素的限制，导致一些问题得不到深入的探究.章末复习课“知新”的环节可以对一些核心知识进行深入的研究，这里通过递进性问题的引导，让学生经历一个由浅入深、由特殊到一般的过程，驱动学生进行思考，经过不断地思考将问题引向深入，加深对知识内涵的理解，从而掌握问题的本质.在此过程中也发展了学生的思维，提升了思维的深度.

3. 笃行：精选典型性例题，提升思维的高度

【教学片段3】

问题1：如图4所示，设A（-3，2）为双曲线y=上一点.

？摇？摇师：如图5，过点A（-3，2）作x轴、y轴的垂线AC，AB，垂足分别为C，B ，求矩形ABOC的面积.

生1：矩形的长和宽分别是3和2，面积是6.

师：如图6，过点A（-3，2）作y轴的垂线AB， 连接AO，求△AOB的面积.

生2：三角形的底和高分别是3和2，面积是3.

生3：三角形的面积是矩形面积的一半，所以面积是3.

思考：过图像上任意一点作两坐标轴的垂线，你能求出所得矩形的面积？作一条坐标轴的垂线，连接原点，你能求出所得三角形的面积吗？

总结：在双曲线下，矩形和三角形的面积模型，S矩形=k，S三角形=.

问题2：如图7所示，点A（-3，2）为双曲线y=图像上一点，过点A作y轴的垂线AB， D为x轴上任意点，求△ABD的面积.

生4：三角形的底和高分别是3和2，面积是3.

生5：连接AO，如图8，△ABD与△ABO同底等高，面积相等，所以面积是3.

师：如图9，延长AO交双曲线于另一点C，连接BC，求△ABC的面积.

生6：点C与点A关于原点中心对称，所以点C的坐标是（3，-2），三角形的底和高分别是3和4，面积是6.

师：为什么点C与点A关于原点中心对称？

生7：双曲线是中心对称图形.

生8：S△ABC= S△ABO+ S△BOC，過C作y轴的垂线CD，如图10，△BOC与△OCD的面积相等，所以S△ABC= S△ABO+ S△DOC，所以面积是6.

师：还是将△BOC回归到刚才总结的模型，运用模型求得△BOC的面积.

师：如图11所示，若点E为双曲线y=图像上任意一点，过点E作y轴的垂线EB，延长EO交双曲线于另一点C，连接BC，你能求△EBC的面积吗？

生9：点E如果运动到点A，就可求得面积是6.

师：你取了特殊值，可以得到答案，但对于任意一点，怎么处理呢？

生10：还是将△EBC的面积看成是△EOB的面积和△BOC的面积的和，可以求得面积是6.

师：通过模型，运用模型求得△EBC的面积.如果除去模型，求三角形的面积要找底和高，你能找到底和高吗？

众生：（沉默）

师：这里的底和高不好找的原因就是E，C两点的坐标不知道，能否引进变量来表示呢？

生11：如图12，设Em，，则点C的坐标为-m，，△ EBC的底和高分别为EB和CD，EB=0-m=-m， CD=-=，所以S△EBC=·（-m）·=6.

师：运用模型可以解决这个问题，通过找三角形底和高常规的方法也可以解决这个问题，模型是在常规方法上的提炼，常规的方法也需要熟练掌握.

思考：用常规方法处理这个问题的过程.

总结：三角形的面积→线段的长→点的坐标→函数关系式.

问题3：如图13所示，点A（-3，2）为双曲线y=图像上一点，过点A的直线y=x+b与双曲线交与另一点B，连接OA，OB，求△AOB的面积.

（过程略）

总结：如图14.

评析  复习课要跳出题海，必须要精选例题，典型例题具有生长功能. 通过一个问题的不断生长，形成一条关联性问题的主线，呈现难题的生长过程，让学生感到难题不再困难，思维得到了训练.这里研究的双曲线下矩形、三角形的面积问题，将反比例函数、一次函数、线段长度、三角形（矩形）的面积等知识联系起来，进而内化方法，形成模型，把双曲线下面积问题解决的方法总结出来，并以此揭示了数形结合、数学模型、转化等数学思想. 用典型例题引导学生不断思考，为学生的思维搭建平台，学生的思维从低点向高端不断进价，提升了思维的高度.

4. 学思：形成联结性体系，建构思维的结构

【教学片段4】

问题：回顾一下本节课复习的内容，总结一下本节课复习了哪些主要的知识点.

生1：复习了反比例函数的定义、图像、性质.

生2：复习了比较大小，反比例函数性质的应用.

生3：复习了反比例图像下面积的求法.

思考：反比例函数这章的知识结构？

总结：如图15.

评析  学思环节，通过梳理知识点，建立知识之间的联系，使知识系统化，在系统中通过结构联系发挥其张力，知识才会牢牢掌握在学生的脑海里;同时也要提炼思想，积累基本活动经验，在精心设计的问题中，使核心知识、技能得到强化，使数学思想方法得到彰显，数学基本活动经验得到体验，学生的思维也会随着形成一条“思维链”，从整体观的视角认识数学知识结构，达到对知识内在基本结构的深度把握，发现背后存在的相同结构，将相同结构迁移到其他内容的学习中去，从而形成良好的思维方式和习惯，培养数学的理性精神.

“学思课堂”章末复习课要依照“学思课堂”的模式，在每个环节的设计中要引导学生的思考方向，促进学生思维的发展.通过对旧知的回顾梳理，理清知识的脉络和内部机构关系，加强对核心知识、技能的巩固，渗透数学思想和方法，形成解决问题的策略.注重思维的发展，挖掘思维的深度，拓宽思维的广度，提升思维的高度，才能形成理性思维的方式和习惯，实现“数学育人”.