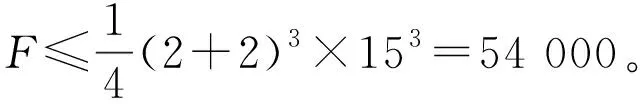单圈图的遗忘指数的上界

周后卿，姚志雄

(1.邵阳学院 理学院，湖南 邵阳，422000；2.邵阳市第一中学，湖南 邵阳，422000)

20世纪70年代，GUTMAN和TRINAJSTIC[1]导出了计算总π-电子能量的近似公式。这些公式中有一项，就是分子图的顶点度的平方和，这个量被认为是对底层分子的碳原子骨架的分支程度的度量。后来被称作第一类Zagreb指数，成为了一个最广泛的基于图的分子结构描述符之一的量的研究。文献[1]中的能量计算公式同样用到了一个量，就是顶点的度的立方和(记作F)，它也是分支的一个度量。但这个量没有被引起注意，以致后来这个量被忘记，所以被称作遗忘的拓扑指数。关于这个拓扑指数的研究文献不多，文献[2]研究了分子图的遗忘指数的一些性质，它与第一类Zagreb指数相结合，具有较大的应用潜力。辛烷值包括沸点、熔点、热容、熵、密度、蒸发热、生成焓、马达法辛烷值、摩尔折射率、偏心系数、总表面积、辛醇-水分配系数、摩尔体积。F指数与上述各项性质相关。与第一类Zagreb指数的结果进行比较，F指数的预测能力与第一类Zagreb指数的预测能力相似，从而看出F指数也是一个比较有用的分子描述符。

定义分子图的遗忘指数F为

通过计算各种化合物和药物分子结构的遗忘拓扑指数，预测新化合物和药物的生物学特性，在医药领域具有重要意义。目前关于F指数的研究文献不多，文献[8]测定了聚丙醚亚胺、卟啉和锌卟啉树枝状大分子的遗忘拓扑指数。文献[9-15]研究了基于图的运算所得到的联图等的遗忘拓扑指数。本文研究基于单圈图的卡氏积图的F指数的界的问题。

1 基本概念和基本性质

首先介绍几个基本的定义与公式。

先介绍几个基本概念及性质。

设f(x)在区间I上有定义，若对于任意x1，x2∈I和t∈(0，1)，有f(tx1+(1-t)x2)≤tf(x1)+(1-t)f(x2)，则称f(x)在区间I上是下凸的；若f(tx1+(1-t)x2)≥tf(x1)+(1-t)f(x2)，则称f(x)在区间I上是上凸的。

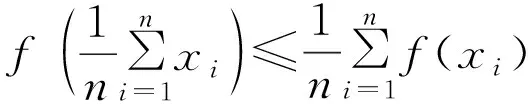
单圈图是指图的顶点数与边数相等的连通图；正则图是指图中每个顶点的度都相等的图；圈图是指每个顶点度为2的连通图。

再看笛卡尔积(简称为卡氏积)图的定义，两个连通图G和H的卡氏积G×H是一个连通图，它的顶点数就是G与H的顶点数的积，即|V(G×H)|=|V(G)|×|V(H)|。

考虑集合

A={((u，v1)，(u，v2))|u∈V(G)且(v1，v2)∈E(H)}

和B={((u1，v)，(u2，v))|(u1，u2)∈E(G)且v∈V(H)}，

卡氏积G×H的边集为E(G×H)=A∪B。从而可推出G×H的边数为

|E(G×H)|=|E(G)|·|V(H)|+|V(G)|·|E(H)|。

对于卡氏积G×H图的最大度，有Δ(G×H)=Δ(G)+Δ(H)。

对于M1和M2，有以下结论。

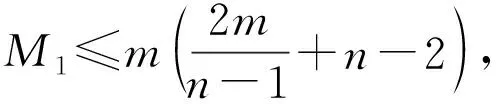
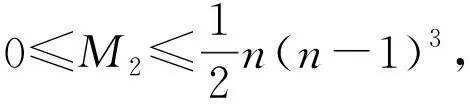
结论3[17]设G是一个具有顶点n、边m、最小度δ的连通图，则

等式成立当且仅当G是星图或完全图。

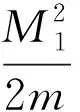
2 引理与定理

本文主要研究单圈图以及几类卡氏积图的遗忘指数问题。

首先给出下列引理。

还需证明下列引理。

引理2设di>0(i=1，2，…，n)，n∈Ν*，当λ>1时，下列不等式成立：

证明令f(x)=xλ，因为f′(x)=λxλ-1，f″(x)=λ(λ-1)xλ-2，当x>0，λ>1时，有f″(x)>0，所以，函数f(x)=xλ为向下凸。

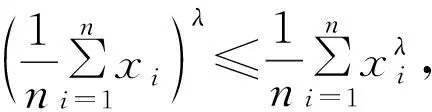
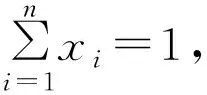
现在给出单圈图的遗忘指数的界。

定理1设图Un是具有顶点n的单圈图，则其遗忘指数满足不等式8n≤F≤2n3，左边等式成立当且仅当Un同构Cn，这里，Cn为圈图。

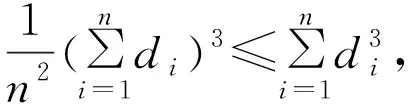
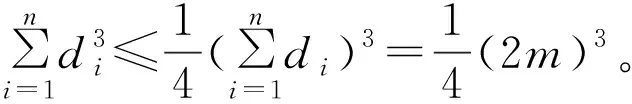
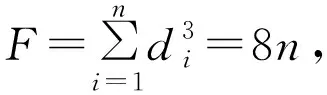
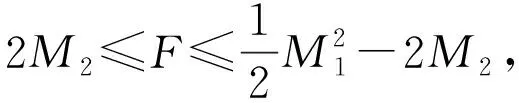
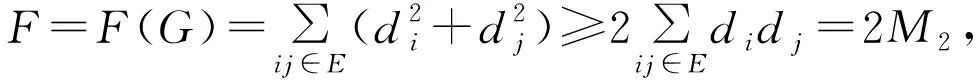
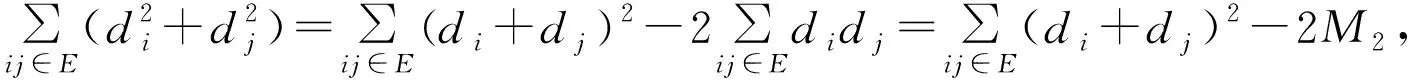
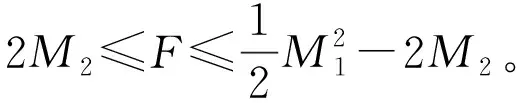
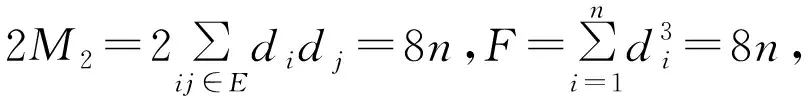
接下来，研究单圈图Gn与单圈图Hm的卡氏积Gn×Hm的遗忘指数的界的问题。给出下列3个图，图1是具有5个顶点的单圈图，图2是1个3圈图，它们的笛卡尔积图如图3所示。

图1 具有5个顶点的单圈图U5Fig.1 Unicyclic graph U5 with 5 vertices

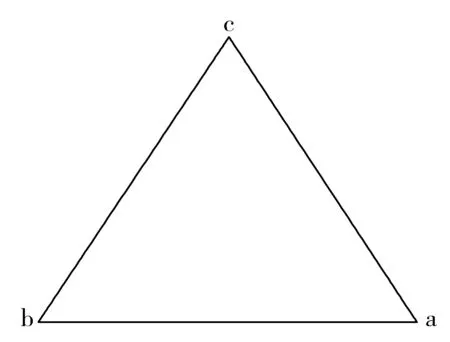
图2 3圈图C3Fig.2 Tricyclic graphs C3

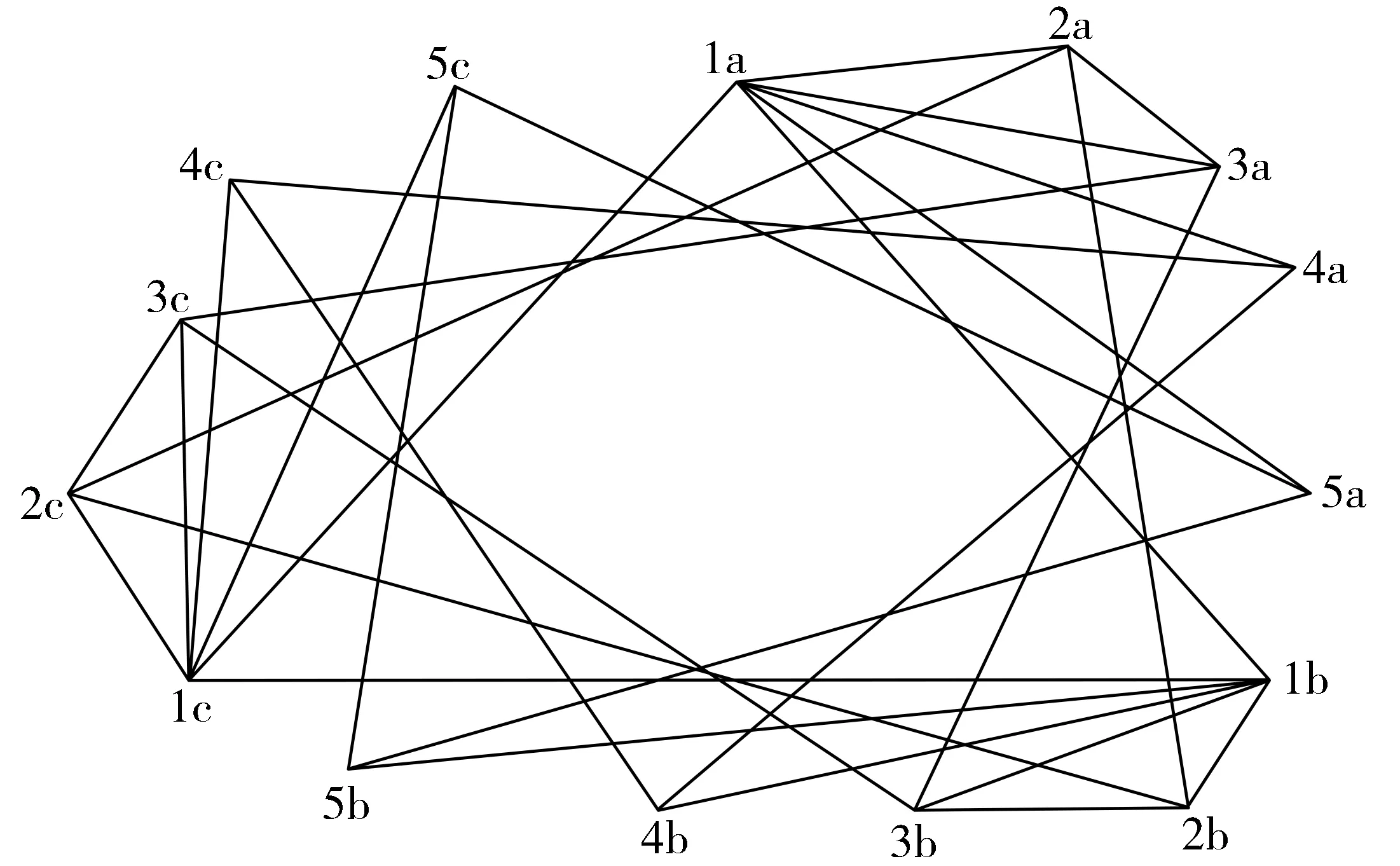
图3 具有15个顶点的卡氏积图U5×C3Fig.3 Cartesian product with 15 vertices U5×C3

定理3 设具有n个顶点单圈图Gn与具有m个顶点的单圈图Hm的笛卡尔积为Gn×Hm，则Gn×Hm的遗忘指数满足不等式F≤16(mn)3。

证明不妨设Gn的顶点集为V(Gn)={1，2，…，n}，Hm的顶点集为V(Hm)={v1，v2，…，vm}，那么Gn×Hm包含有mn个顶点，它的顶点度之和可以表示成

由引理2有

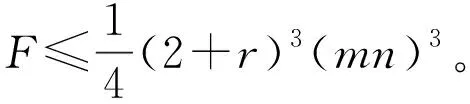
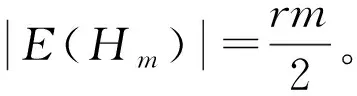
因为Gn×Hm包含有mn个顶点，它的顶点度之和可以表示成

所以，根据引理2得