矩阵方程AXB+CXD=F的参数迭代法

2021-01-05陈兴团马昌凤

邵阳学院学报（自然科学版） 2020年6期

陈兴团，马昌凤

(福建师范大学数学与信息学院，福建福州，350117)

矩阵方程常常在多个领域出现，如控制理论[1-2]、系统理论[3-4]、稳定性理论以及一些纯应用数学理论。因为矩阵方程[5-13]的应用比较广泛，所以，许多学者都致力于对它进行研究。有很多方法可以用来求解矩阵方程，如共轭梯度法[14-15]、矩阵分解法等，本文提出了一种参数迭代法[16-19]来求解矩阵方程。还有一些其他方法，见参考文献[20-24]。

设A，B，C，D∈Cn×n，考虑矩阵方程

AXB+CXD=F

(1)

方程(1)仅有一解的充要条件是BT⊗A+DT⊗C的特征值不为零。若B和C均为可逆矩阵，则矩阵方程(1)等价于

(C-1A)X+X(DB-1)=C-1FB-1

(2)

方程(2)仅有一解的充要条件是C-1A与DB-1没有互为反号的特征值。此外，如果A，B，C和D都是埃尔米特正定矩阵时，那么，BT⊗A+DT⊗C也是埃尔米特正定矩阵，从而方程(1)有唯一解。

1 参数迭代法的建立与收敛性分析

选取实数α≠0，使αB+D和αC+A均为可逆矩阵，令

(3)

即

(4)

将方程(1)两端乘以α，得

αAXB+αCXD=αF

X=MXN+Y0

(5)

易见，方程(5)与方程(1)等价。下面将给出相应的参数迭代格式：

X(k+1)=MX(k)N+Y0，k=0，1，…

(6)

利用拉直算子将式(6)转化为列向量形式

vec(X(k+1))=(NT⊗M)vec(X(k))+vec(Y0)，k=0，1，…

(7)

式(7)是一阶线性定常迭代格式，它的迭代矩阵为NT⊗M，且有

ρ(NT⊗M)=ρ(NT)ρ(M)=ρ(M)ρ(N)。

有如下的收敛性定理。

定理1对任意给定的初始矩阵X(0)，格式(6)收敛的充要条件是ρ(M)ρ(N)<1。

证明当矩阵C可逆时，设M的任一特征值为λM，对应的特征向量为x，则有Mx=λMx，利用式(3)可求得

(8)

(9)

即M的特征值可由C-1A的特征值表示。

当矩阵B可逆时，设N的任一特征值为λN，则λN也是NT的一个特征值，记对应的特征向量为y，则有NTy=λNy，利用式(3)可求得

(10)

(11)

即N的特征值可由DB-1的特征值表示。

定理2设B和C都可逆，对任意给定的初始矩阵X(0)，格式(6)收敛的充要条件是

(12)

证明类似于定理1。

推论1若B和C是可逆矩阵，并且DB-1和C-1A的特征值实部都大(小)于零，则可得对任意正(负)数α，格式(6)收敛。

证明由上述可知，若矩阵B可逆，且DB-1的特征值的实部都大于零，可得μj>0；若矩阵C可逆，且C-1A的特征值的实部都大于零，可得ηi>0；又由于α为正数，则有

即有格式(6)收敛。同理可证，当B和C都可逆，并且DB-1和C-1A的特征值的实部全都小于零，这样对任意负数α，格式(6)收敛。证毕。

从定理1可以得到，仅需选取适当实数α，使得ρ(M)ρ(N)<1，那么格式(6)就能够收敛，这样子问题就转化为怎么样选取该实数α，才会使得格式(6)收敛最快，即ρ(M)ρ(N)最小，因此，将使得ρ(M)ρ(N)达到最小的实数α=αopt，称为格式(6)的最优参数。

2 最优参数的选取

在这一小节中，将讨论如何选取格式(6)的最优参数，若矩阵A，B，C和D都是埃尔米特正定的。由于

故C-1A和DB-1的特征值全为正数。由上述推论1知道，对于任意的正数α，迭代格式(6)是收敛的。设C-1A和DB-1的特征值排序为

η1≥η2≥…≥ηn，μ1≥μ2≥…≥μn

(13)

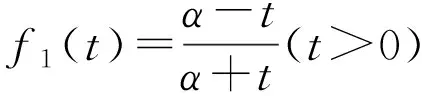
(14)

(15)

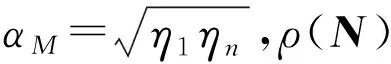
由式(14)和(15)可得

(16)

当得到迭代格式(6)的最优参数即知道了αM和αN的取值时，便可计算C-1A和DB-1的最大和最小特征值。为了避免计算C-1和B-1，给出了最优参数αM和αN的近似取法。

定理4设A，B，C和D都是埃尔米特正定矩阵，且它们的特征值依次为

a1≥a2≥…≥an，b1≥b2≥…≥bn，

c1≥c2≥…≥cn，d1≥d2≥…≥dn，

证明根据广义特征值问题的极值原理，由式(8)可得(下面的最大值和最小值是针对0≠x∈Cn来求取的)：

(17)

(18)

(19)

易见ρ(M)≤q(α)。要让ρ(M)最小，只需使q(α)最小即可。因此，可得使q(α)达到最小的实数为

据式(13)，正数η1，ηn，μ1，μn之间的关系可归结为以下6种：①ηn≤μn≤η1≤μ1；②ηn≤μn≤μ1≤η1；③ηn≤η1≤μn≤μ1；④μn≤ηn≤μ1≤η1；⑤μn≤ηn≤η1≤μ1；⑥μn≤μ1≤ηn≤η1。

定理5在引理1的条件下，若

(20)

则αopt=αM；否则，αopt=αN。

证明对关系式①有αM≤αN，令

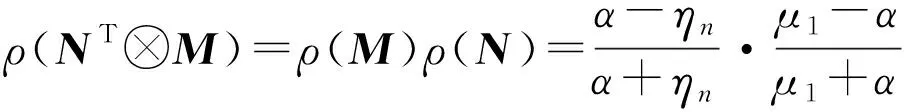
可得

改写式(20)为

(21)

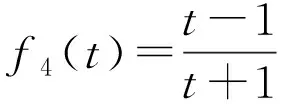
或者

由引理1中的关系式②的证明过程知αopt=αN。

同理可证，对关系式③～⑥，定理也成立。证毕。

3 加速的参数迭代法

下面讨论关于迭代格式(6)的加速方法。

若取初始向量X(0)=Y0时，则由数学归纳法可得，迭代格式(6)可写为

(22)

由定理1可知，当ρ(NT⊗M)<1时，上述迭代格式收敛，且有

(23)

其中：X*是原方程的精确解。

(24)

其中：S(0)=X(0)=Y0。

于是由式(24)可得部分和的迭代格式为

S(k+1)=S(k)+M2kS(k)N2k，S(0)=Y0，k=0，1，…

(25)

4 数值实验

下面将给出几个矩阵方程数值例子来说明参数迭代法的有效性和可行性。以下2个实验都是在Windows 10系统下Matlab R2014b的环境下运行的。

例1考虑矩阵方程AXB+CXD=I，其中，

则C-1A和DB-1的特征值分别为

η1=6.411 5，η2=1.815 2，η3=0.773 3，

μ1=1.153 5，μ2=0.660 5，μ3=0.064 0。

根据定理3求得αM=2.226 7，αN=0.271 8。由式(16)求得

ρ(M)|αM=0.484 5，ρ(N)|αN=0.618 7。

由定理5知αopt=αM。

B和D的特征值分别为

b1=5.247 0，b2=3.555 0，b3=2.198 1，

d1=4.791 3，d2=2.000 0，d3=0.208 7。

根据给出的A，B，C和D，分别用迭代格式(6)和(24)求解，假设终止条件为10-10，若对于不同的参数α，初始矩阵为X(0)=Y0，则数值结果见表1。

表1 不同α对于例1的数值结果Table 1 Numerical results about different α for Case 1

从表1可以看出，对于迭代格式(6)而言，取不同的参数α，迭代次数也发生变化，选取最优参数，则可在一定程度上降低迭代所需的次数，α越接近最优参数，迭代次数越少。而对于加速的迭代格式(24)而言，在同样的参数取值下，它所需要的迭代次数明显少于迭代格式(6)的迭代次数，这说明了加速的参数迭代法是有效的，并且可以提高迭代格式(6)的收敛速度。

例2设A，B，C和D都是分块的三对角矩阵，即

其中：

表2 不同α对于例2的数值结果Table 2 Numerical results about different α for Case 2

从表2中可以发现：若取α=0.02，则迭代格式(6)需要迭代479次，但迭代格式(24)只需要迭代10次即可满足精度要求；若取α=1.076 0，可知迭代格式(6)要迭代11次，而迭代格式(24)仅仅需要迭代4次就能满足精度要求。因而，计算最优参数有助于选取合适的α，从而降低迭代次数和时间。加速的参数迭代法有较快的收敛速度，从而提升了实验效率。