基于SMT求解器的微处理器指令验证数据约束生成技术
2021-01-05罗巧玲王丽一胡夏晖
谭 坚 罗巧玲 王丽一 胡夏晖 范 昊 徐 占
(江南计算技术研究所 江苏无锡 214083)
随着计算机体系结构理论与技术的迅速发展、制造工艺水平不断提升以及集成电路设计日趋复杂,行业内科研人员设计实现的处理器逻辑功能变得越来越复杂,对处理器测试验证质量的要求越来越高.为保证处理器功能正确性,硬件设计人员、验证人员、系统软件测试人员甚至用户都或多或少会承担着处理器功能与性能的测试验证任务.指令级功能测试是处理器正确性验证的重要组成部分,贯穿处理器研制过程中的各个阶段,在软件模拟指令验证、FPGA(field programmable gate array)实物验证、硬件模拟仿真验证以及SoC(system on chip)硅后验证等阶段都需要进行充分验证;指令级测试方法具有通用性的特点,与具体的处理器类型无关,在专用处理器与通用处理器研制过程中都需要用到,其实现方法依赖于指令语义、内部规范以及指令上下文等.
在开展指令级功能测试的过程中,我们发现对于测试方案所要求覆盖的部分特殊场景,采用现有模拟验证方法较难达到目的.例如,当需要对单指令的结果进行各种数据类型的遍历验证时、在约定浮点操作数的中间结果为某特定数值时、在约定2个操作数之间满足特定关系时尤其是约定输入操作数与输出操作数之间满足特定的约束关系时,采用现有主流的模拟验证方法[1]通常显得比较低效.此外,很多的指令功能是隐含一些特定的约束关系,如加减法、乘法指令运算时存在进、借位情况发生的可能.这些内部关系对于测试人员来说不直接,部分约束甚至需要处理器设计人员协助制定.采用现有模拟方法,在制定测试验证计划或者生成测试程序的时候很难全面覆盖,即使能够实现代价也比较大.以上提及的场景都是比较常见的验证功能点,要求测试人员必须覆盖.
面对结果操作数与指令内部关系进行约束的验证场景,如果采用功能模拟测试方法,通常需要测试人员根据指令的语义模拟出该指令的相反语义,将输出转换成模拟程序的输入,反推出指令的输入操作数,形成验证元组数据,再根据验证数据生成相应的指令测试激励,验证指令功能正确性.部分指令其实是没有严格意义对应的求反过程的,例如浮点指令,假若存在浮点操作数A×B=C,但是由于舍入模式等原因,导致数据元组A,B,C在很多时候并不满足C/B=A的关系.
因此,对于系统测试人员而言,很多的待验证场景采用现有的功能模拟等手段是比较难以实现的;即使采用算法模拟成功实现,得到验证数据的运行时间通常较长,生成的数据量也比较有限.
国内外处理器设计研发机构如Intel,IBM等公司,为满足处理器特殊约束场景的验证需求,组织了大量的科学家专门设计了满足各自处理器约束建模需求的求解器[2-3].根据IBM公司官网显示,以色列海法实验室研究开发出了GEC(generation core),Stocs,Mage等专用求解器[4],并在此基础上开发出了Genesys-Pro[5],FPgen[6]等一系列系统,很好地满足了处理器验证过程中面临的各种功能验证需求.由于这些求解器的实现与处理器内部设计细节紧密相关,因此这些专用求解器仅限在公司内部以及合作单位进行应用.
由于与设计紧密关联并且需要参考模型等底层环境和技术的支撑配合,目前现有以功能模拟为基础的系统级测试很难全面覆盖带约束的待测场景.很多带约束的待测场景对系统级测试人员来说是可见的,因此将会使系统测试在功能覆盖方面存在不足.如果不加以覆盖,将会导致经过系统测试的目标处理器仍然存在设计错误的隐患,这对处理器研制来说是不能容忍的.随着形式化技术的快速发展,我们可以在系统级测试过程中引入形式化方法,对指令约束关系描述并建模求解.在验证场景与处理器功能测试覆盖任务之间建立可靠的技术桥梁,满足工程实际需要,提升处理器验证测试质量.
本文首先对一种形式化技术方法——可满足模理论(satisfiability modulo theory, SMT)[7]进行简要介绍;然后提出了一种基于SMT求解器的关系约束求解技术,分别从指令结果操作数约束、操作数相互关系约束、指令内部关系约束以及浮点操作数约束4个方面,阐述SMT技术在解决指令功能关系约束建模需求时的具体实现方法,给出了具体约束建模求解算法;之后,指出了求解过程中存在的常见问题并有针对性地提出了优化策略;最后,我们对SMT技术在指令功能验证中的应用进行了总结,对后续进一步工作进行了展望.
1 可满足模理论概况
可满足模理论(SMT)是基于布尔命题可满足问题(Boolean satisfiability problem, SAT)发展起来的一种形式化技术.其中SAT求解器能够判定给定的合取范式(conjunctive normal form, CNF)是否存在可以满足的模型,即判别是否存在满足所有给定公式都为真的变量赋值.SAT求解技术在微处理器RTL(register transfer level)级约束验证中被广泛应用.研究人员开发了很多成熟的SAT求解器;这些求解器被当作一种基础支撑的问题判定技术,已经广泛应用于人工智能领域和其他问题求解项目中.SMT技术是在SAT命题逻辑的基础上扩充了量词和项,融合了多种背景知识理论,提升了问题描述能力,扩充了应用求解范围.
SMT求解器支持用户定义变量、声明变量之间约束关系,将用户自定义的约束描述自动转换成命题逻辑甚至谓词逻辑公式,然后通过一定的搜索策略、调用底层SAT求解器进行问题判定求解;问题可满足时将给出一个满足所有约束关系的随机模型,对用户定义的变量进行随机赋值,否则求解器将反馈问题是不可满足的.
SMT有很多种具体的、被广泛使用的求解器,各个求解器之间的背景理论存在差别,因此不同求解器有各自擅长的问题求解领域.其中比较通用的是Alt-Ergo,OpenSMT,veriT,Yices,CVC3/CVC4,Z3等,其中微软公司的Z3、斯坦福大学和爱荷华州立大学联合开发的CVC4求解器尤为突出.Z3支持比特位向量、整型、实数、浮点等数据类型的变量定义与约束关系描述.支持空理论、数组、字符串、线性算术运算、非线性运算、集合运算、差分逻辑、命题逻辑、谓词逻辑等运算关系表达,甚至可以将不同领域的知识进行组合,实现复杂问题的求解[8].CVC4支持实数和整型的线性算术运算、数组、元组、归纳数据类型、比特位向量、字符串、等式与未解释函数等理论运算[9].SMT求解器强大的表达能力在实际问题的建模与求解方面有着广泛的技术前景[10-12].
本文正是利用SMT求解器强大的问题描述能力,对指令功能验证中存在比较复杂的内部约束关系进行建模.借助SMT求解器自动判断与可满足情况下随机模型生成的能力特征,生成测试验证数据,达到在处理器系统级测试任务中覆盖复杂场景的目的.
2 基于SMT求解器的指令操作数约束求解技术
系统级测试中基于约束的指令功能验证可通过对指令操作数施加约束,利用求解器建模验证是否满足给定的约定操作数,生成验证元组数据形成对应的测试激励,验证目标机器是否满足该约束对应的验证数据.本节针对模拟验证方法不便覆盖的4种情形,说明采用SMT求解器实现指令功能约束求解技术的优越性.
本文中提及的建模描述以及约束求解实验是采用Z3求解器,原因是其能够提供多种语言的支持以及API接口,同时能够支持描述浮点、整型、比特位等数据类型;提供了广泛的逻辑运算接口,能够对指令集涉及到的多种微指令行为建模提供很好的支持,同时能够以字符串的方式对求解结果进行输出,方便用户获取求解结果以及后续数据的处理.实验求解器不仅限于Z3,有资料显示CVC4最新版本[13-14]已经能够支持浮点类型数据,因此也能够实现本文中提到的建模描述实验的所有过程.
2.1 结果操作数约束
模拟验证方式对于很多指令的结果操作数不能直接、高效地进行约束求解.例如无符号乘法指令MULRa,Rb,Rc实现Rc=Ra×Rb的功能,这里3个操作数均为无符号整型类型.如果用户需要对Rc进行数据类型遍历,同时限定Rb是大于1的整数.那么需要求解Ra,则需要测试人员模拟出形如Ra=RbOPRc,然后制定相应算法实现求解.然而很多时候存在实现代价太大甚至是无法求解的情形.但这时候采用SMT求解器则很容易表达与求解,因为其背景理论支持各种算术表达式的约束求解.对于约定Rc≡111,同时要求Rb为大于1的整型数据,那么要求解满足条件的Ra,用户可以采用如下伪代码约束表达方式进行描述:
①args[0]=mk_gt(Rb,1);…/*描述Rb>1的约束*/;
②args[1]=mk_mul(Ra,Rb,Rc);…/*描述Rc=Ra×Rb的约束*/;
③args[2]=mk_eq(Rc,const_111); …/*描述Rc≡111的约束*/;
④clause=mk_and(args,3); …/*描述同时满足上述3个约束*/.
其中mk_gt,mk_mul,mk_eq,mk_and都是SMT求解器算子,Ra,Rb,Rc则是用户使用SMT求解器API声明的变量;mk_gt(Rb,1)描述的是Rb>1的约束关系;mk_mul(Ra,Rb,Rc)描述的是Rc=Ra×Rb的约束关系;mk_eq(Rc,111) 描述的是Rc≡111的约束关系.然后将以上3个约束关系分别赋值给args[0],args[1],args[2]子公式中,clause=mk_and(args,3)描述的是将上述3个公式进行合取并赋值给CNF公式clause.
上述结果操作数约束伪代码采用Z3求解器建模描述得到CNF范式以及随机求解模型结果如表1所示:

Table 1 Result Operand Constraint CNF Formula and Solution in Z3 Solver表1 结果操作数约束Z3建模CNF公式以及求解模型
最后,形成的公式clause表示需要满足所有3个约束关系;利用SMT求解器进行求解,求解器在运算过程将始终保持上述3个约束条件,如果有解,则系统将返回满足所有上述约束条件的一组Ra,Rb,Rc的随机赋值.
对于其他复杂语义的指令,可以通过增加约束变量以及借助SMT支持的命题逻辑运算符进行描述,实现给定约束的建模描述.
2.2 操作数之间关系约束
模拟验证的方式在对操作数之间的约束关系描述时也存在不足之处.例如对测试要求对操作数之间关系进行约束.仍然以无符号乘法MULRa,Rb,Rc为例.如对测试数据进行约束,要求遍历Rc的数值中1的个数从0~64的所有情况,同时要求Ra或者Rb中1的个数不能多于Rc中1的个数.这时采用模拟验证的方式就很难高效地实现.
相对而言,采用SMT求解器虽然也是比较复杂但仍然能够相对方便地进行表述与求解.
用户可以增加变量N1,N2,…,N64,分别对应Rc中最低n位中1的个数,可以采用4个步骤实现约束建模:
①args[0]=mk_ite(extract(Rc,0,0),(N1=1),(N1=0)); …/*抽取Rc的第0位进行判断:如果Rc[0]=为1,则N1赋值为1,否则赋值为0*/;
②args[j]=mk_ite(extract(Rc,i,i),(Ni+1=Ni+1),(Ni+1=Ni));…/*抽取Rc中的第i位判断:如果Rc[i]=1,则Ni+1赋值为Ni+1,否则Ni+1赋值为Ni*/;
③ …/*依此类推,建立Rc所有的位计数约束关系,再分别建立Ra或者Rb的位计数约束关系N_Ra[i]*/;
④ 最后args[k]=mk_le(N_Ra[64],N64).
其中mk_ite,extract,mk_le是SMT求解器算子:mk_ite描述的是一种if-then-else的约束关系;extract实现的是抽取SMT变量的某几个位的功能;mk_le描述的是一种小于等于的约束关系.
mk_ite(extract(Rc,i,i),(Ni+1=Ni+1),(Ni+1=Ni))描述的是抽取Rc中的第i个位并进行判断:如果Rc[i]=1,则Ni+1赋值为Ni+1,否则Ni+1赋值为Ni.
通过上述关系的描述,系统将合取所有公式集合,形成满足所有上述约束条件的公式,以此作为求解器的输入进行约束求解.在约束可满足时,系统将随机给出满足所有子公式约束的模型,测试人员可以根据模型形成验证数据,并由此生成覆盖特殊场景的测试激励.
上述操作数之间关系约束伪代码采用Z3求解器建模描述得到CNF范式以及随机求解模型结果如表2所示.为简化描述,这里仅给出满足上述条件且在Rc的操作数位表示法中1的个数为8的情况.
2.3 指令内部关系约束
如果测试验证人员关心计算结果中是否出现进借位的场景,采用SMT求解也是能够实现该场景约束的表达并求解.本节以64 b的无符号加法ADDLRa,Rb,Rc为例进行说明.
当约定ADDL操作为无符号长字加法以及所有操作数的值是无法确定结果是否存在进位的,因为结果约束最多就约束了64 b.但是计算时可能发生Ra+Rb得到的有效位实际上是超过64b的情形.为达到加法进位场景覆盖验证的目的,我们继续给出这种情况SMT求解器的约束建模过程:

Table 2 The CNF Formula of Relational Constraints Between Operands and Solution in Z3 Solver表2 操作数之间关系约束Z3建模CNF公式 以及求解模型
①args[0]=mk_eq(Rc_64,extract(Rc_65,63,0));…/*约束Rc_64与Rc_65的最低64 b相同*/;
②args[1]=mk_eq(Ra_64,extract(Ra_65,63,0));…/*约束扩展源操作数最低64 b与原始源操作数相同*/;
③args[2]=mk_eq(Rb_64,extract(Rb_65,63,0));…/*同上*/;
④args[3]=mk_eq(Rc_64,mk_add(Ra_64,Rb_64));…/*分别建立结果操作数Rc与未扩展之前的Ra和Rb之间的关系*/;
⑤args[4]=mk_eq(Rc_65,mk_add(Ra_65,Rb_65));…/*建立扩展之后的结果操作数与扩展之后的源操作数之间仍然需要保持原约束关系*/;
⑥args[5]=mk_eq(1,extract(Rc_65,64,64));…/*获取Rc_65的最高位并约定其为1,描述发生进位约束的情况*/;
⑦args[6]=mk_not(mk_eq(1,extract(Ra_65,64, 64)));…/*获取Ra_65的最高位并约定其不等于1*/;
⑧args[7]=mk_not(mk_eq(1,extract(Rb_65,64, 64)));…/*获取Rb_65的最高位并约定其不等于1*/.
其中mk_add是SMT求解器算子,描述的是一种加法运算;mk_not描述的是公式求反运算,mk_eq,extract与2.2节描述功能相同.
上述操作数之间关系约束伪代码采用Z3求解器建模描述得到CNF范式以及随机求解模型结果如表3所示:
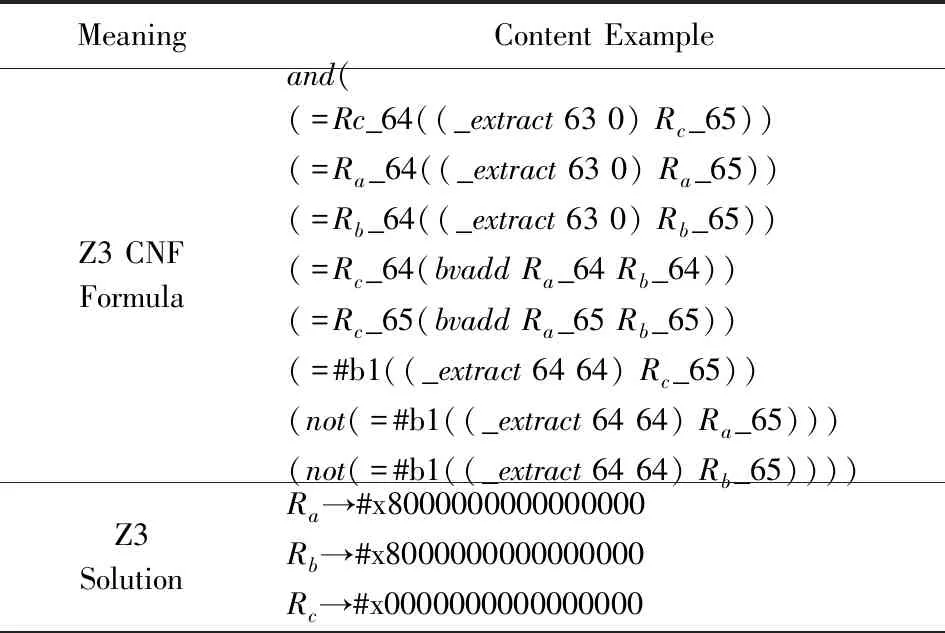
Table 3 CNF Formula of Instruction Internal Relationship Constraint and Solution in Z3 Solver表3 指令内部关系约束Z3建模CNF公式以及求解模型
2.4 浮点操作数约束表示
浮点部件作为处理器的重要部件,再加上浮点数据组成特殊性,因此浮点运算指令的正确性验证历来都是测试验证的重点.Z3求解器能够同时支持位、整型、浮点等数据类型,另外还支持多种舍入模式,支持半精度、单精度、双精度、128 b浮点以及其他自定义格式的浮点运算,并且支持IEEE-754 2008标准,因此可使用Z3求解器灵活构建多种测试需求的浮点运算约束求解模型.
对浮点操作数约束通常存在2种方式:第1种是直接通过求解器接口构建不同类型的浮点数据类型,例如正负零、规格化数、非规格化数、无穷大以及非数等;第2种是采用位方式分别构建浮点的符号位、指数位与尾数位,然后通过拼接以上3部分形成需要验证的浮点数据,如首先拼接成64 b的长整型数据,然后采用内部接口转换成浮点数据类型,通过约束符号位、指数位、尾数位的方式实现浮点数据约束的目的.结合前述分析以及对浮点结果操作数的约束覆盖需求,采用模拟验证方式也是存在不足的.
以双精度浮点加法运算FADDD为例,假设测试人员需要验证舍入模式为向零舍入、浮点加法结果操作数的尾数为0x123456的非规格化数且输入操作数都是规格化数的情况.我们继续以伪代码方式给出这种验证需求时采用SMT求解器的约束建模过程:
①args[0]=mk_fp_normal(x);…/*约束第1个输入操作数为规格化数*/;
②args[1]=mk_fp_normal(y);…/* 约束第2个输入操作数为规格化数*/;
③args[2]=mk_fp_subnormal(x_plus_y);…/*约束输出操作数为非规格化数*/;
④args[3]=mk_eq(x_plus_y,mk_fp_add(mk_fp_rtz,x,y));…/*约束输出操作数x_plus_y等于x与y在舍入模式为向零舍入下的浮点加法运算结果*/;
⑤args[4]=mk_eq(x_plus_y,mk_fpa_to_fp_bv(mk_concat(sign_x,mk_concat(exp_x,mant_x)),dp_sort));…/*约束将sign_x,exp_x,mant_x进行拼接并形成dp_sort类型的浮点数据,同时进一步约束拼接之后的结果等于x_plus_y*/;
⑥args[5]=mk_eq(mant_x,mk_unsigned_int64(0x123456,bv_sort(52)));…/*约束尾数为操作数0x123456*/;
⑦clause=mk_and(6,args);
最后对前6个约束进行与运算,即同时满足以上6个约束,形成公式clause作为求解器的输入进行约束求解.对应的Z3建模过程以及求解结果如表4所示:

Table 4 CNF Formula of Float-Point Instruction FADDD Constraint and Solution in Z3 Solver表4 浮点指令FADDD约束的Z3建模CNF 公式以及求解模型
通过以上4种典型情况的展示,测试人员可基于该技术进一步扩展并解决绝大多数计算类指令操作数约束测试覆盖的验证求解需求.在解决约束表达与求解的问题之后,测试人员则可以将更多的时间精力放到测试场景的构建中,确保覆盖更多、更特殊情况的测试场景,提高测试针对性和测试质量,有效提升测试覆盖率.
3 求解优化技术
采用SMT对测试场景进行约束建模与求解的过程中,往往会遇到约束遍历求解耗时较长的问题,尤其是在涉及较多约束变量、关系较为复杂的情况下,求解时间可能会非常长.
在指令约束建模编码的实践过程中,通过SMT技术建立的求解程序通常是由若干个子问题的求解过程组成.而单次求解是1个单线程串行计算过程.当某个求解耗时很长甚至时无解时,求解器可能长时间悬挂在某一次求解的情况,导致后续求解必须等待前面的求解结束之后才能继续的问题.经过作者分析与实践,发现很多求解器都提供了超时终止求解的功能.针对该问题,SMT用户在构建求解框架时,通过设定时间阈值,系统将在求解开始之后进行计时,若给定时间耗费完之后仍然不能判定出问题是否可满足时,系统将终止本次求解过程;转而继续后续的求解判定.这样就可以避免整个求解模型挂死在单个无效问题求解的情形.通过实现参数化框架,用户可以根据模型求解的特征,对不同的约束模型设定不同的时间阈值,保证约束求解不会因为时间阈值的限制导致求解质量明显下降.
本文作者还发现在构建遍历所有约束条件的模型求解程序中,各个子约束求解过程相互之间是松耦合的.通过约束模型求解的合理设计与组织,不同求解过程是可以拆解成相互独立的计算过程.这为采用并行化技术加速整个框架求解提供了可能.作者将耦合度不高的模块分布到不同的线程,由各个线程并行独立求解,所有线程求解结束之后将结果进行整合,形成统一的约束求解数据集合.
本文作者在实践过程中成功实现了一种基于多进程与多线程相结合的并行求解框架:顶层使用fork函数创建多个进程、在单个进程中创建多个线程的方式,实现将原本顺序、串行的遍历约束求解过程分散到N×M个线程中,充分利用当前服务器的计算资源进行问题求解,利用消耗空间资源换取时间,结合超时终止求解的技术,采用参数控制的形式,实现有限时间内对指令约束模型的并行求解框架.框架实现流程如图1所示:

Fig. 1 Schematic diagram of parallel acceleration solution model based on fork and thread technologies图1 基于fork+thread的并行加速求解模型示意图
使用4.8.4版本的Z3求解器,在1台具有2个物理CPU、累计56个逻辑核心、每个核心支持双线程的Intel服务器上进行实验,初始时将并行求解框架中进程数N与线程数M分别设置8和4.
同时我们选择了ADDL、MULL以及逻辑运算指令LOG2XX这3条指令,分别对指令的约束求解模型加速前后的效果进行比较分析.其中ADDL模型相对简单,求解建模实现时仅有6个约束变量、针对5个约束关系形成了5个公式,运行过程中单次求解时间相对较短;MULL指令复杂度次之,建模约束个数较多、求解时间较ADDL长.LOG2XX指令则较为复杂,根据指令语义每种数据类型遍历的情况下存在16个不同的操作码,分别定义了8个约束变量,对约束变量建立的约束关系超过128个,求解时间相对较长.
此外,实验过程中将单次求解的时间阈值设置为1 s,即1 s内如果约束公式不能判定是否有解则终止,转而对下一约束关系模型进行求解.如图2所示,每条指令均选择了4组数据,分别对应了单种约束情况下求解得到1,10,100,1 000组随机模型的情况.这里的1,10,100,1 000分别对指令的每一个操作数、每一种操作数数据类型进行完全遍历时在每种情况下运行的求解次数.需要说明的是,实验中设置的每种情况1次随机模型时,ADDL与MULL对应的模型将累计产生32次有效求解,LOG2XX指令将累计产生超过480次有效求解.3条指令的在串、并行模式下运行求解时的加速比分别如图2所示:

Fig. 2 Parallel acceleration diagran in 8×4 configuration图2 在8×4配置下的并行加速示意图
通过分析,我们看到在累计使用32个线程并行加速的情况下,ADDL在4种情况下实际得到的单次有效求解加速比最高可达6.11,MULL指令模型最大可达12.22,LOG2XX最大可达10.74.数据显示,在相同约束求解模型内,随着求解次数的增加,总体加速效果越好.尽管没有达到N×M=32的加速比,但是相比串行顺序求解的方式,并行求解模型的加速效果依然非常明显.
为了进一步获取更高的加速比,我们调整N与M的数值关系,分别在针对3种指令模型在单种约束情况下得到1 000组随机求解模型的前提下开展对比试验,得到的加速效果如图3所示.从图3中还可以看到,在支持双线程的服务器上,采用16×2模式的并行求解框架能够获得更好的加速效果.同时也可以看到,不合理的进程数与线程数设置甚至可能起不到加速的效果,并且在3种指令模型求解加速效果均支持这个结论.因此应根据实际的服务器配置采用不同的进程数与线程数的设置,达到更快生成指令验证元组数据的效果.
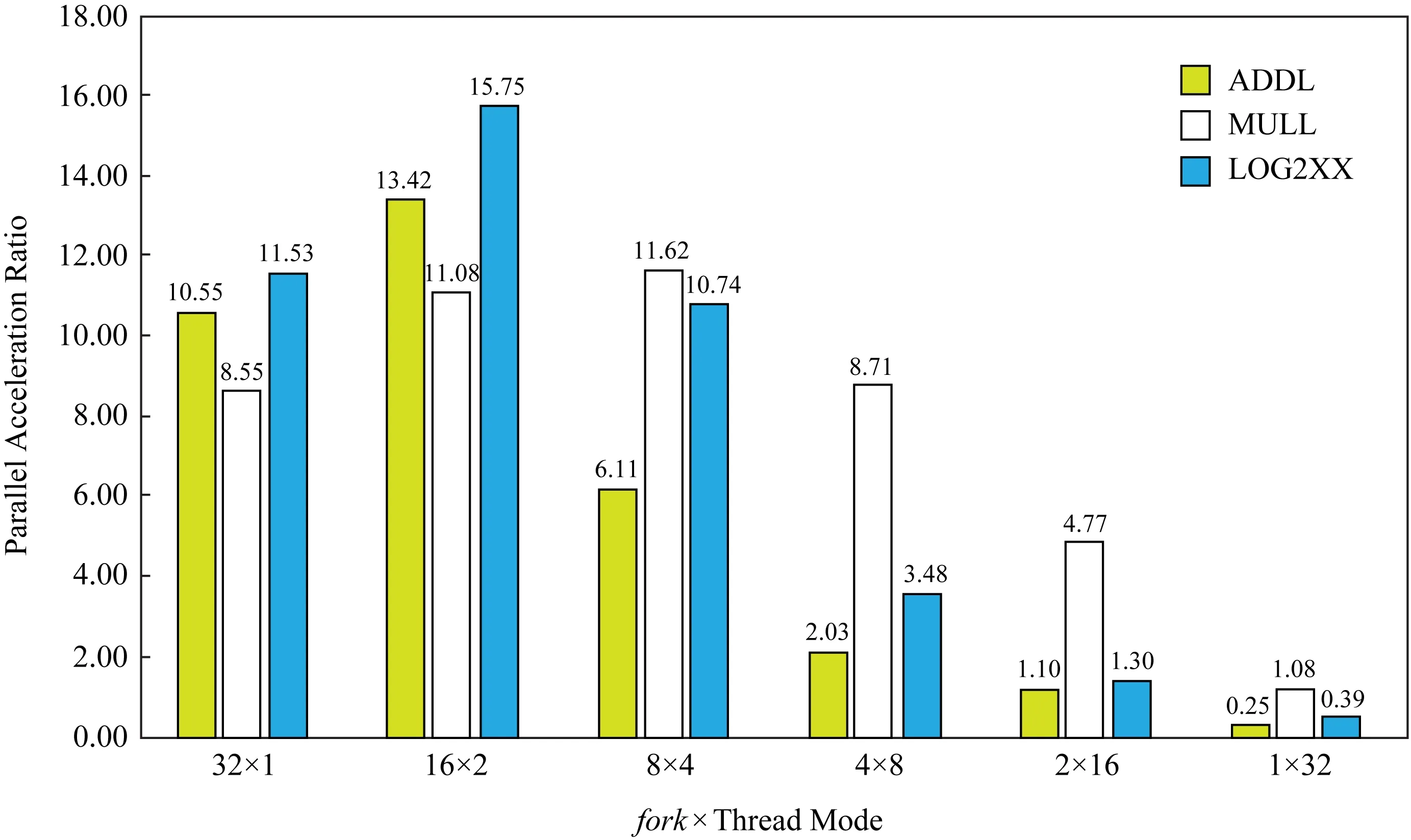
Fig. 3 Parallel acceleration diagram in multiple configurations图3 多种配置下的并行加速示意图
综上所述,通过比较3种指令约束模型的求解时间,我们看到复杂模型的求解时间较长,在约束复杂度相同的情况下,求解时间基本与求解数目成线性关系;不同模型之间,复杂度较大的模型加速效果较为明显;初步结论显示,随着约束模型的复杂度增加和求解次数增多,采用合理进程数与线程数配置的并行求解模型可得到较为理想的加速效果.
4 结论与未来工作
基于模拟验证的指令功能测试方法在结果操作数约束、操作数之间的约束、指令内部约束以及浮点操作数约束情形中存在不足,我们提出了一种基于SMT求解器的指令操作数约束求解技术.针对这4种场景,分别给出了详细的建模描述过程与求解结果示意.针对模型求解过程中存在求解时间较长的问题,采用时间阈值机制、超时则终止当前求解的策略;同时利用进程与线程管理技术,牺牲CPU计算资源换取时间的策略,对指令约束模型实现求解加速.实验结果表明,时间阈值策略与合理的进程加线程的并行框架提升了模型求解效率.
根据本文提出的方法实现生成的测试验证数据与程序,已成功应用于国产神威系列处理器的测试验证工作中,发现了一些隐藏较深的设计问题;同时能够支持在系统级甚至用户级层面更加深入地验证设计弱项、实现复杂场景的覆盖,如辅助特殊边界场景的异常测试验证.实践表明,采用SMT指令级约束求解技术基本能够实现系统级测试指令功能验证任务中各种场景的建模描述与求解的功能需求,为测试实施人员提供可靠的技术支撑.
通过与公开报道的IBM,Intel公司关于指令级功能与数据约束求解方面的技术特征进行比较,利用本文提出的方法与思路基本可实现指令集的功能约束、数据路径约束等主要指令级约束建模求解.同时由于借助了SMT强大的约束表达能力,测试人员甚至可以仅仅根据设计规范说明文档进行功能与数据路径的约束建模,弱化约束求解对设计实现的依赖,更加灵活地在处理器系统级测试验证工作中实现约束求解功能,进一步提升测试质量.
在今后的工作中,我们将继续探索SMT技术在复杂约束生成、指令序列约束等验证场景中的应用前景;进一步探索优化约束求解技术,充分利用现有商用处理器资源,寻找加速模型求解的有效途径;尽可能在短时间内生成更多的验证测试数据,更全面、更高效地满足处理器研制过程中的功能正确性覆盖需求,不断提升处理器系统测试的质量.
