利用地下水填充钻孔的埋管换热器性能分析*

蒋坤卿，黄思浩，李华山，卜宪标

利用地下水填充钻孔的埋管换热器性能分析*

蒋坤卿1,4，黄思浩1,4，李华山1,2,3，卜宪标1,2,3†

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院可再生能源重点实验室，广州 510640； 3. 广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4. 中国科学院大学，北京 100049）

地下水填充的井下换热器（GFBHE）是一种不需要灌浆，利用地下水填充钻孔进行换热的地热换热器。针对GFBHE建立了瞬态三维数值模型进行模拟，并与利用普通灌浆材料进行回填的埋管换热器进行对比。数值模型通过将孔隙型岩层等效为饱和多孔介质的方法将钻孔外部的自然对流现象考虑在内。研究了包括渗透系数、地温、钻孔孔径在内的关键因素对GFBHE性能的影响。结果表明，当含水层渗透系数大于1×10−4m/s时，GFBHE性能明显优于利用灌浆填充钻孔的地热换热器，在富水区域利用GFBHE取代后者是可行的。GFBHE的换热性能随着钻孔孔径、含水层渗透性的增大以及地温的升高而提升。

地热能；埋管换热器；传热；数值模拟；多孔介质

0 引 言

随着世界经济的持续发展，人类对能源的消耗量日益增加。在过去的几十年里，人类的能源消耗量增加了一倍[1]。目前，化石能源依旧主导着世界能源结构，化石能源的大量消耗给环境带来了巨大压力，因此有必要进行节能以减少化石能源的消耗。目前普遍认为建筑节能是各种节能途径中最有效且潜力最大的方式[2]。地源热泵（ground source heat pump, GSHP）作为一种地热能利用形式，在世界范围内得到了广泛的应用，被应用于建筑的供暖以及提供生活热水等。地热换热器（borehole heat exchanger, BHE）是地源热泵系统的一个重要组成部分。最常见的BHE是将换热管置于钻孔内，并利用回填材料填充U型管与钻孔壁之间的环空来保持钻孔稳定以及强化传热[3-7]。除此之外，也有利用地下水填充钻孔的BHE形式（groundwater-filled borehole heat exchanger, GFBHE），这种BHE通常在强岩层区域进行钻孔，地下水通过岩石的裂隙自然地流入钻孔中[8]。GFBHE结构简图如图1所示。在灌浆填充的钻孔中，主要的传热方式是导热；在由水进行填充的钻孔中，主要的传热方式是自然对流传热，有时还受到含水层地下水平流的影响[9]。利用地下水填充钻孔由于不需要填充材料可以减少初投资，相比水泥灌浆也能减少建设时间[10]。并且已有的研究也表明这种BHE具有可靠的传热性能[11-12]，甚至还有人提出了在密封良好的钻孔中注入人造液体取代传统灌浆的新型BHE结构[13]。

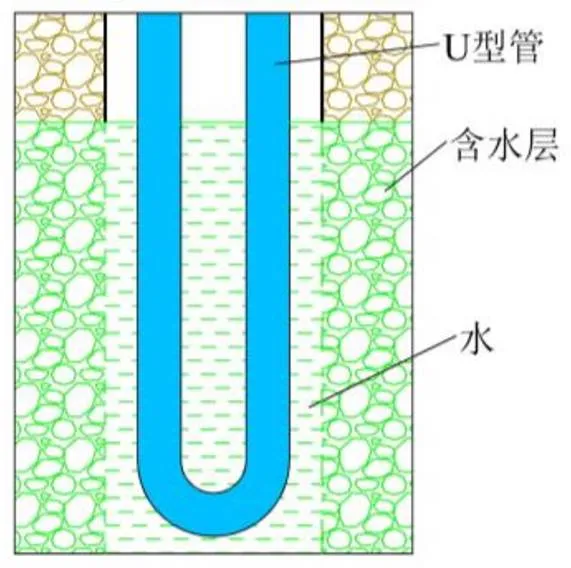
图1 GFBHE结构简图

目前，已经有学者对GFBHE进行了研究。GEHLIN等[14]对热响应测试中由温度变化引起岩层裂隙中的自然对流进行了定性研究。GUSTAFSSON等[8,15]利用热响应测试分析不同地质条件下，换热流体注入温度和流速对钻孔内外热阻的影响。JAVED等[16]提出了适用于GFBHE的热响应测试评估方法。

作为一种有效的手段，数值模拟的方法也被应用到GFBHE的研究中[9,11-12,17-19]。GUSTAFSSON等[11]利用数值模拟软件FLUENT建立了一个3 m长的BHE模型，其研究重点是钻孔内部的自然对流，没有考虑含水层的渗透性。HOLMBERG等[17]针对GFBHE提出了一种简化的数值模型，发现钻孔内部的热阻在取热以及放热的不同运行模式下会有较大的不同。SPITLER等[9]得出了钻孔内部的努塞尔数与修正的瑞利数相关的结论。SHI等[19]对比研究了不同结构的换热器在地下水横流以及自然对流共同作用下的表现。JOHNSSON等[12]证明了钻孔内自然对流的存在，得出钻孔内水的有效导热系数的范围为1 ~ 2 W/(m∙K)。

如前所述，已经有许多研究者针对GFBHE利用热响应测试以及数值模拟的方法进行了研究。然而，热响应测试并不能真实地反映出GFBHE在冬季工况下的性能表现；已经建立的数值模型也大多数没有考虑发生在含水层内部的自然对流现象，而根据已有的研究，钻孔周围的对流现象会影响换热器的换热性能[20-23]。考虑到GFBHE的应用环境往往具有渗透性良好的条件，钻孔外部的对流传热也应考虑到模型之中。本文从GFBHE的实际应用环境出发，建立GFBHE的三维数值模型，并与灌浆填充的BHE（grout-grouted BHE, GGBHE）进行对比。研究两种BHE在相同环境和运行条件下的性能差异以及影响GFBHE性能的关键因素，分析在富水区域利用GFBHE取代传统灌浆BHE的可行性，让更多人认识到GFBHE的使用价值，为地热换热器的建设提供更多选择。

1 模型描述

1.1 模型假设

为了完整地描述GFBHE的传热过程，建立了耦合导热以及对流的三维非稳态数值模型。模型涉及U型管内外的对流传热以及钻孔与含水层之间的换热，现作出以下假设：

（1）含水层被视为均质且各向同性的饱和多孔介质；

（2）忽略地下水横流，仅考虑自然对流的作用；

（3）忽略地温梯度，认为含水层初始水温分布均匀。

上述假设对GGBHE模型同样适用。

1.2 数值模型

1.2.1 连续性方程

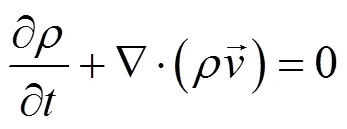
1.2.2 动量守恒方程

流体的动量守恒方程如下：

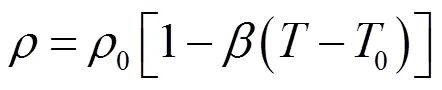
多孔介质区域的动量方程可以通过在式（2）的基础上加入动量源项的方式实现，由于本文不考虑地下水的横流对传热的影响，只考虑由BHE换热引起的自然对流，而由自然对流引起的水流速度不高，因此多孔介质中的水流可通过达西定律进行描述：

式中：为流体黏度；为渗透率。

1.2.3 能量方程

单一流体的不可压缩流能量方程有如下形式：

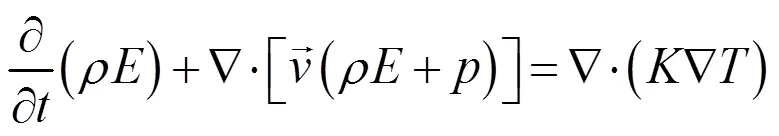
对于不可压缩流，式（5）中总能由下式表达：

固体区域能量方程形式如下：

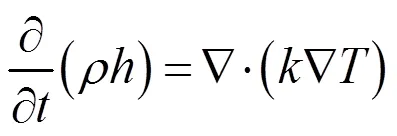
式（6）和式（7）中，为比焓，其表达式为：

其中：C为相应介质的比热容；ref为参考温度。

多孔介质中的传热过程采用热平衡假设模型[24]进行描述，即认为在传热过程中多孔介质固相以及液相的温度保持一致。多孔介质的能量方程如下：

式中：f为流体总能；s为固体比焓；f为液体密度；s为固体密度；f为液体导热系数；s为固体导热系数；e为等效导热系数；为孔隙率。

2 基本模拟参数

本文U型管换热器的材料采用较为常见的高密度聚乙烯管。基于对比分析的出发点，两种BHE的基本结构参数相同。模型的整体直径为15 m，钻孔和含水层的长度均为80 m，直径为130 mm；U型管外径为25 mm，壁厚2.5 mm，管中心距60 mm。默认的含水层孔隙率为0.3，渗透系数为1 × 10−5m/s。假设含水层的初始平均温度为20℃。换热器入口水流速度设置为0.5 m/s，入口水温为5℃。忽略模型上下面的传热，模型的侧面边界设置为恒温边界条件。其他参数如表1所示。

表1 模拟用到的物性参数

3 结果与讨论

GFBHE换热过程复杂，涉及的影响因素较多，本文主要对比分析包括渗透系数、钻孔孔径、岩石导热系数在内的因素对GFBHE以及GGBHE性能的影响，并分析两种BHE的运行特性。模拟所涉及的含水层渗透系数的参数变化范围在1×10−5~ 1×10−3m/s之间，含水层温度的变化范围在10 ~ 30℃之间，钻孔直径变化范围在110 ~ 190 mm之间。本文所进行的研究仅针对冬季工况展开。

3.1 两种BHE的运行特性分析

图2是GFBHE和GGBHE在默认条件下模拟120 h得到的出口温度变化曲线。从图中可以看到，在默认的条件下GFBHE的出口温度（out）始终高于GGBHE，这在一定程度上体现了GFBHE的可靠性能。在模拟的时间范围内，GFBHE和GGBHE的平均换热功率分别为3 270.8 W和2 915.8 W，GFBHE的换热性能要略优于GGBHE。此外，从图中还可以看出，两种BHE的出口温度变化趋势相同，在模拟进行的前20 h内出口温度都迅速降低，之后温度变化逐渐趋于平缓，120 h左右时，出口温度已经相对稳定。因此接下来将取模拟第120 h的结果来分析两种BHE的运行特性，并研究不同因素对两种BHE性能的影响。

图2 两种BHE出口水温随时间的变化

图3 渗透系数为1×10−3 m/s时两种BHE运行120 h后含水层不同深度位置温度分布情况

图3显示了GFBHE和GGBHE在渗透系数为1×10−3m/s时运行120 h后钻孔周围不同深度位置含水层温度变化情况，其中表示含水层深度位置，横坐标表示距钻孔轴心的距离。可以看到，GGBHE钻孔周围不同深度的温度分布几乎相同，图中各点温度高度重合，而GFBHE钻孔周围不同深度温度分布则有极大的不同。显然，越靠近含水层底部，GFBHE钻孔周围的含水层温度变化越大，其热影响范围也越大，说明GFBHE的热提取过程更倾向在含水层底部进行。基于有关深井换热器的报道[25-27]，推测两种BHE运行特性的不同是由于GFBHE钻孔内的水可以自由地在含水层与钻孔内进行交换造成的。钻孔内参与换热的冷流体在进入含水层之后受重力的影响向含水层底部流动，随着换热的不断进行，冷流体不断在底部聚集使含水层底部的热影响范围逐渐扩大。而GGBHE由于不存在GFBHE的这种特性难以在含水层建立起足够强度的自然对流，不能充分发挥含水层的自然对流换热作用。

图4 钻孔及含水层内部流线和温度分布图

为验证上述推测绘制了含水层和钻孔内的流线图与温度云图。从图4中可以看到，钻孔内的水自上而下流动，在靠近钻孔底部的位置进入含水层，而含水层内的水在靠近上方的位置进入钻孔，实现了钻孔内外的冷热流体交换；含水层只有在靠近钻孔下方的位置有比较明显的温度场变化。

3.2 含水层渗透系数对两种BHE性能的影响

不同渗透系数下，两种地热换热器平均功率的对比如图5显示。从图中可以看出，GFBHE的换热功率随着渗透系数的增大而增大，在渗透系数小于1×10−4m/s时，渗透系数的改变对GFBHE换热性能影响相对较小，当渗透系数大于1×10−4m/s时，渗透系数的改变对GFBHE的性能影响较大。此外，从图中还可以看到GGBHE换热性能受渗透率改变的影响并不明显。

图5 两种BHE的平均换热功率随渗透系数的变化

图6所示为两种BHE在不同渗透系数下进出口温差随时间的变化情况，图中GGBHE的进出口温差曲线几乎重合，而GFBHE的进出口温差曲线则明显受到渗透系数的影响，渗透系数越大，进出口温差越大。因此含水层渗透率越高的地区使用GFBHE得到的收益更大。含水层的渗透性越好，钻孔内外的原水交换就越容易，原水交换的同时，实现了对井内外换热效果的提升。而GGBHE没有钻孔内外的原水交换，对于含水层的渗透性变化的不敏感也从侧面说明了钻孔内外原水交换的重要性，因此在高渗透性含水层使用GGBHE可能无法充分利用含水层的渗透性来提升地热换热器的效果。当然，只有在渗透系数大于1×10−4m/s时，GFBHE的换热效果提升才比较明显。

图6 不同渗透系数下进出口温差变化情况

3.3 钻孔直径对两种BHE性能的影响

钻孔直径是BHE在建设过程中的一个重要参数，钻孔直径的选择不仅影响BHE的换热效果，也影响BHE的建设费用，因此本节对比分析两种BHE在不同孔径下的运行特性。在模拟过程中发现，GGBHE换热功率随孔径大小变化趋势与LUO等[28]的描述不符，分析认为这是由于灌浆材料导热能力的差异造成的。目前大多数灌浆材料的导热系数集中在0.8 ~ 2.4 W/(m∙K)之间[29]，而导热系数的大小是灌浆材料的一个重要特性。因此，为了使对比结果更加可靠，人为地将灌浆的导热系数修改为1.5 W/(m∙K)和2.5 W/(m∙K)进行模拟，并将所有模拟结果绘制在图7中，GGBHE、GGBHE-1.5和GGBHE-2.5分别代表灌浆导热系数为0.93 W/(m∙K)、1.5 W/(m∙K)和2.5 W/(m∙K)的GGBHE。从图7中可以看到GFBHE的换热能力完全可以与GGBHE相比。而且随着孔径的增大，GFBHE的换热性能也相应提高。当孔径为190 mm时已经可以和灌浆导热系数最大的GGBHE性能非常接近。而GGBHE的性能随孔径的变化情况则随着灌浆导热系数的变化而有所不同，导热系数较小的GGBHE换热能力随孔径的增大而减小，而采用较大导热系数的GGBHE性能则随孔径的增大而有所提高。

图7 两种BHE的平均换热功率随孔径的变化情况

图8显示了GFBHE钻孔空间中水的平均流速随孔径的变化情况，可以看到钻孔内水的平均流速随着孔径增大而增大，而水流速度的提升有利于对流传热。对于GFBHE换热性能随孔径增大而提升的特性，认为是由于钻孔空间的增大使得钻孔内的自然对流作用增强引起的。因此，建议在建设GFBHE的过程中，在费用允许的前提下尽量使用较大的钻孔孔径。

图8 GFBHE钻孔内水的平均流速随孔径的变化

3.4 含水层温度对两种BHE性能的影响

GFBHE传热的关键在于自然对流传热过程，而自然对流由温差进行驱动，可以预测GFBHE的换热性能受含水层温度的影响较大。图9显示了两种BHE在不同的地温条件下的换热功率以及出口温度变化情况。可以看到两种BHE的换热功率以及出口温度都随着含水层温度的升高而升高。但两种BHE换热性能的增长速度并不相同，GFBHE的换热功率增长曲线斜率更大。在含水层温度为10℃时两种BHE的换热性能不相上下，随着含水层温度的升高，GFBHE相对GGBHE的性能提升越来越明显。因此温度越高的含水层，使用GFBHE可以获得更好的换热性能。

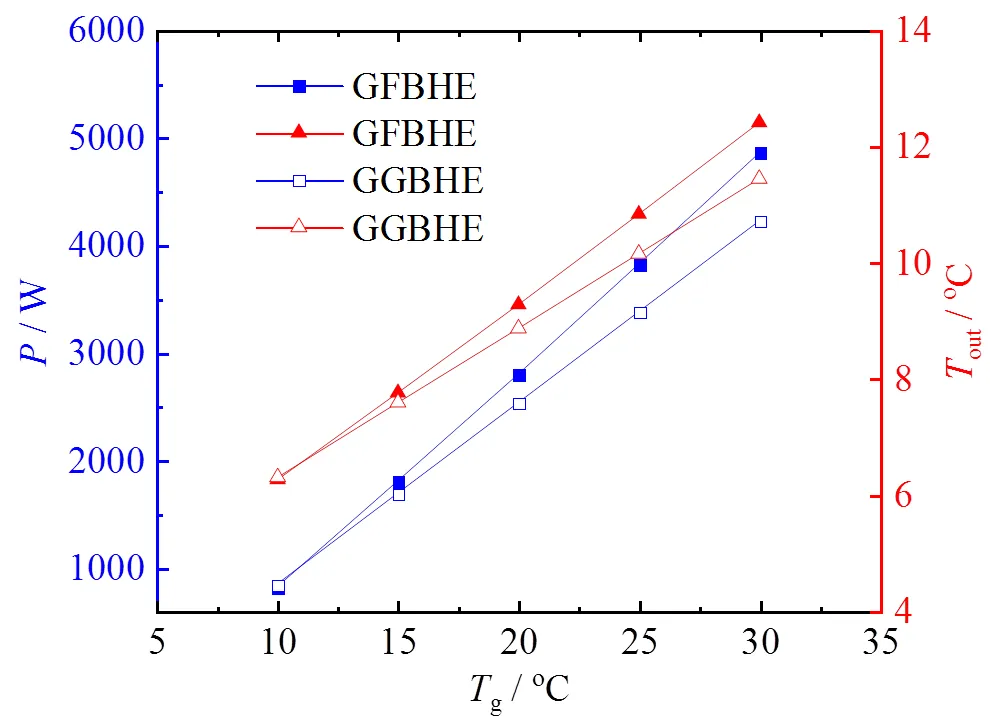
图9 两种BHE在不同地温条件下的换热功率及出口温度

4 结 论

针对GFBHE和GGBHE建立了三维非稳态数值模型并进行了求解，对比分析了GFBHE和GGBHE的性能差异，研究了包括渗透系数、钻孔孔径、含水层温度在内的关键因素对两种BHE性能的影响。主要结论如下：

（1）含水层渗透性对GFBHE的影响较大，对GGBHE的影响不明显。当渗透系数大于1×10−4m/s时，随着渗透系数的增大，GFBHE的换热性能明显提升，当渗透系数小于此值时，渗透系数的变化对GFBHE的影响相对较小。

（2）在冬季工况下，随着含水层温度的升高，GFBHE和GGBHE的换热功率都在提升。但是，GFBHE换热功率变化曲线斜率比GGBHE的要大，说明随着地温的升高GFBHE性能提升更大。

（3）GFBHE的性能随着钻孔孔径的增大而升高。GGBHE换热性能随孔径变化情况则与灌浆的导热能力有关，采用导热能力小的灌浆的GGBHE性能随孔径增大而下降，反之，则提升。

总之，在富水条件下建设GFBHE取代传统的灌浆BHE是可行的，并且由于节省了灌浆的费用，GFBHE的经济性可能会更好。此外，从各因素对两种BHE的影响来看，越是高渗透性以及高地温的地区使用GFBHE效果越好，建造GFBHE时也应该有意使用较大的孔径以获得更好的换热效果。

[1] KONTOROVICH A E, EPOV M I, EDER L V. Long-term and medium-term scenarios and factors in world energy perspectives for the 21st century[J]. Russian geology and geophysics, 2014, 55(5/6): 534-543. DOI: 10.1016/j.rgg.2014.05.002.

[2] 江亿. 我国建筑耗能状况及有效的节能途径[J]. 暖通空调, 2005, 35(5): 30-40. DOI: 10.3969/j.issn.1002-8501. 2005.05.007.

[3] BEIER R A. Transient heat transfer in a U-tube borehole heat exchanger[J]. Applied thermal engineering, 2014, 62(1): 256-266. DOI: 10.1016/j.applthermaleng.2013.09.014.

[4] BORINAGA-TREVIÑO R, PASCUAL-MUÑOZ P, CASTRO-FRESNO D, et al. Study of different grouting materials used in vertical geothermal closed-loop heat exchangers[J]. Applied thermal engineering, 2013, 50(1): 159-167. DOI: 10.1016/j.applthermaleng.2012.05.029.

[5] BOUHACINA B, SAIM R, OZTOP H F. Numerical investigation of a novel tube design for the geothermal borehole heat exchanger[J]. Applied thermal engineering, 2015,79: 153-162. DOI: 10.1016/j.applthermaleng.2015.01.027.

[6] 刁乃仁, 曾和义, 方肇洪. 竖直U型管地热换热器的准三维传热模型[J]. 热能动力工程, 2003, 18(4): 387-390. DOI: 10.3969/j.issn.1001-2060.2003.04.015.

[7] 方肇洪, 刁乃仁, 曾和义. 地热换热器的传热分析[J]. 工程热物理学报, 2004, 25(4): 685-687. DOI: 10.3321/ j.issn:0253-231X.2004.04.046.

[8] GUSTAFSSON A M, WESTERLUND L. Heat extraction thermal response test in groundwater-filled borehole heat exchanger–Investigation of the borehole thermal resistance[J]. Renewable energy, 2011, 36(9): 2388-2394. DOI: 10.1016/j.renene.2010.12.023.

[9] SPITLER J D, JAVED S, RAMSTAD R K. Natural convection in groundwater-filled boreholes used as ground heat exchangers[J]. Applied energy, 2016, 164: 352-365. DOI: 10.1016/j.apenergy.2015.11.041.

[10] CHOI W, OOKA R. Effect of natural convection on thermal response test conducted in saturated porous formation: Comparison of gravel-backfilled and cement- grouted borehole heat exchangers[J]. Renewable energy, 2016, 96: 891-903. DOI: 10.1016/j.renene.2016.05.040.

[11] GUSTAFSSON A M, WESTERLUND L, HELLSTRÖM G. CFD-modelling of natural convection in a groundwater-filled borehole heat exchanger[J]. Applied thermal engineering, 2010, 30(6/7): 683-691. DOI: 10.1016/j.applthermaleng.2009.11.016.

[12] JOHNSSON J, ADL-ZARRABI B. Modelling and evaluation of groundwater filled boreholes subjected to natural convection[J]. Applied energy, 2019, 253: 113555. DOI: 10.1016/j.apenergy.2019.113555.

[13] FOCACCIA S, TINTI F. An innovative Borehole Heat Exchanger configuration with improved heat transfer[J]. Geothermics, 2013, 48: 93-100. DOI: 10.1016/j.geothermics. 2013.06.003.

[14] GEHLIN S E A, HELLSTRÖM G, NORDELL B. The influence of the thermosiphon effect on the thermal response test[J]. Renewable energy, 2003, 28(14): 2239-2254. DOI: 10.1016/S0960-1481(03)00129-0.

[15] GUSTAFSSON A M, WESTERLUND L. Multi-injection rate thermal response test in groundwater filled borehole heat exchanger[J]. Renewable energy, 2010, 35(5): 1061-1070. DOI: 10.1016/j.renene.2009.09.012.

[16] JAVED S, NAKOS H, ClAESSON J. A method to evaluate thermal response tests on groundwater-filled boreholes[J]. ASHRAE transactions, 2012, 118(1): 540-549.

[17] HOLMBERG H, ACUÑA J, NÆSS E, et al. Numerical model for non-grouted borehole heat exchangers, Part 2—Evaluation[J]. Geothermics, 2016, 59: 134-144. DOI: 10.1016/j.geothermics.2014.11.002.

[18] LYU Z H, SONG X Z, LI G S, et al. Numerical analysis of characteristics of a single U-tube downhole heat exchanger in a geothermal well[J]. Geothermics, 2018, 72: 15-23. DOI: 10.1016/j.geothermics.2017.10.012.

[19] SHI Y, SONG X Z, LI G S, et al. Numerical investigation on heat extraction performance of a downhole heat exchanger geothermal system[J]. Applied thermal engineering, 2018, 134: 513-526. DOI: 10.1016/j.applthermaleng.2018.02.002.

[20] CAROTENUTO A, CASAROSA C, DELL'ISOLA M, et al. An aquifer-well thermal and fluid dynamic model for downhole heat exchangers with a natural convection promoter[J]. International journal of heat and mass transfer, 1997, 40(8): 4461-4472. DOI: 10.1016/S0017-9310(97)00052-5.

[21] DIAO N R, LI Q Y, FANG Z H. Heat transfer in ground heat exchangers with groundwater advection[J]. International journal of thermal sciences, 2004, 43(12): 1203-1211. DOI: 10.1016/j.ijthermalsci.2004.04.009.

[22] WANG H J, QI C Y, DU H P, et al. Thermal performance of borehole heat exchanger under groundwater flow: a case study from Baoding[J]. Energy and buildings, 2009, 41(12): 1368-1373. DOI: 10.1016/j.enbuild.2009.08.001.

[23] GHOREISHI-MADISEH S A, HASSANI F P, MOHAMMADIAN A, et al. A transient natural convection heat transfer model for geothermal borehole heat exchangers[J]. Journal of renewable and sustainable energy, 2013, 5(4): 043104. DOI: 10.1063/1.4812647.

[24] NIELD D A, BEJAN A. Convection in porous media[M]. New York: Springer Science+Business Media, 2013.

[25] CAROTENUTO A, MASSAROTTI N, MAURO A. A new methodology for numerical simulation of geothermal down-hole heat exchangers[J]. Applied thermal engineering, 2012, 48: 225-236. DOI: 10.1016/j.applthermaleng.2012. 04.021.

[26] FREESTON D H, PAN H. The application and design of downhole heat exchanger[J]. Geothermics, 1985, 14(2/3): 343-351. DOI: 10.1016/0375-6505(85)90073-2.

[27] LUND J W. The use of downhole heat exchangers[J]. Geothermics, 2003, 32(4/6): 535-543. DOI: 10.1016/j. geothermics.2003.06.002.

[28] LUO J, ROHN J, BAYER M, et al. Thermal performance and economic evaluation of double U-tube borehole heat exchanger with three different borehole diameters[J]. Energy and buildings, 2013, 67: 217-224. DOI: 10.1016/ j.enbuild.2013.08.030.

[29] EROL S, FRANÇOIS B. Efficiency of various grouting materials for borehole heat exchangers[J]. Applied thermal engineering, 2014, 70(1): 788-799. DOI: 10.1016/ j.applthermaleng.2014.05.034.

Performance Analysis of Buried Pipe Heat Exchanger Filled with Groundwater

JIANG Kun-qing1,4, HUANG Si-hao1,4, LI Hua-shan1,2,3, BU Xian-biao1,2,3

(1. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 2. CAS Key Laboratory of Renewable Energy, Guangzhou 510640, China; 3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640, China; 4. University of Chinese Academy of Sciences, Beijing 100049, China)

Groundwater-filled borehole heat exchanger (GFBHE) is a kind of geothermal heat exchanger which does not need grouting and uses groundwater to fill the borehole for heat exchange. A transient three-dimensional numerical model of GFBHE was established and compared with the buried pipe heat exchanger grouted with common grout material. The numerical model took the natural convection outside the borehole into account by equivalent the porous rock to the saturated porous medium. The influence of key factors including permeability, ground temperature and borehole diameter on GFBHE and cement-grouted buried pipe heat exchanger was studied. The results showed that when the permeability coefficient of aquifer was larger than 1 × 10−4m/s, the performance of GFBHE was obviously superior to the geothermal heat exchanger using grouting to fill the borehole, and it was feasible to use GFBHE to replace the latter in water-rich areas. The heat transfer performance of GFBHE was enhanced with the increase of borehole diameter, aquifer permeability, and ground temperature.

geothermal energy; borehole heat exchanger; heat transfer; numerical simulation; porous media

2095-560X（2020）06-0470-07

TK529

A

10.3969/j.issn.2095-560X.2020.06.004

蒋坤卿（1996-），男，硕士研究生，主要从事地热能开发与利用方面的研究。

卜宪标（1979-），男，博士，研究员，主要从事地热能开发与利用方面的研究。

2020-07-29

2020-08-22

国家自然科学基金项目（41972314）

卜宪标，E-mail：buxb@ms.giec.ac.cn