区域生态效率测度及其空间分异特征——基于PCA的三阶段DEA模型

余华银 江艳婷（安徽财经大学统计与应用数学学院，安徽蚌埠233030）

一、综述

近年来我国经济增长态势良好，2019年GDP 增速为6.3%，但随之而来的资源消耗与环境污染问题已经成为经济增长的焦点，如何实现资源、环境与经济的协调发展成为我国亟须解决的问题。生态效率是指资源环境投入与经济产出的比值，其效率值恰能反映三者持续协调发展的状况，为了深入探究各省市资源消耗过度、环境投入过多的原因及区域协调发展的差异性，对各省市进行真实的生态效率测度是迫切需要的，以便各省市根据自身协调发展的现状做出改进措施，朝着推动中国整体生态效率稳步提升的目标前进。

生态效率一直是学者们研究的热点，为了提高生态效率，社会在提供产品与服务的同时要尽可能把生态影响降到最低，即实质是如何获得单位资源环境成本下的高经济产出或者单位经济产出下的低成本。生态效率的测度首先关乎到指标选取问题，kuosmanen 指出单一指标无法进行生态效率测度[1]；mickwitz 等亦认为应该构建多维综合指标全面测度生态效率，但不应主观赋权[2]，因此为了避免主观因素干扰，学者们广泛采用数据包络分析方法（DEA），即运用统计方法客观赋权，研究要素的投入与产出关系。程晓娟采用DEA 模型从资源、环境两个维度对中国区域生态效率进行评估[3]；杨斌采用DEA模型对我国生态效率进行评价研究，并指出粗放型经济向集约型经济的转变是提高生态效率的关键[4]。由于单一的DEA模型包含了环境因素与随机因素的影响无法测算客观真实的效率值，因此Fried 等提出了三阶段DEA 模型，要求所有的决策单元处于相同的环境与运气水平下，测算出真实的技术管理水平[5]，随后被广泛运用于生态效率的测算，如邓波等采用三阶段DEA 测算2008年我国30 个省市的生态效率值，在剔除环境因素与随机因素影响前后，生态效率值产生了较大变化，但其在构建指标体系时，缺乏对水资源、土地资源投入的研究[6]；牛建广等运用三阶段DEA 测算2014年我国31个省市的生态效率值，研究发现三阶段DEA 模型能真实测度我国各区域生态效率发展现状，但其没有考虑社会资源投入对生态效率的影响[7]。

通常DEA 模型要求决策单元的数量是投入产出之和的两倍，这样，系统信息才能被真实反映。鉴于此，运用主成分分析法获得综合指标不仅能提取指标的重要信息，还能缩减投入产出指标数量，所以PCA—DEA 模型被国内外学者广泛应用，如Azadeh[8]和Adler[9]，以及刘小娜运用PCA—DEA 研究我国2016年的区域生态效率[10]，但学者们对于PCA—三阶段DEA 的研究较少，因此，本文尝试把PCA 与三阶段DEA相结合，对我国30 个省、市、自治区2011—2017年间的生态效率值（未包括西藏，因其部分数据未统计；未包括香港、澳门、台湾）进行整体和局部的评价，探讨我国生态效率发展现状并基于外部环境的影响提出切实可行的建议。

二、研究方法

（一）主成分分析

主成分分析的思想是从几个单一指标中提取重要信息，形成能够反映某一事物特征的综合指标，在对区域生态效率分析评价中，具有代表性的数据变量较多，而且变量间存在不同程度的相关性，因此需采用PCA 降维的方式提取综合指标，结果可以控制信息损失的同时提高分析效率，并有利于后续问题的研究。

（二）三阶段DEA

1.第一阶段DEA

本文基于我国生态发展的现状与规律，在第一阶段选择投入导向的BCC 模型进行生态效率值的测算，其中，X、Y 分别是投入、产出值，ε 为非阿基米德无穷小量，θ 代表效率值，λ 表示权重，S 为松弛变量，模型一般表示如下：

投入变量的松弛变量，包含了管理水平、环境因素与随机误差的影响，为了剔除环境因素与随机因素的影响，得到能真实反映技术管理水平的生态效率值，运用随机前沿模型SFA 将投入松弛变量对环境变量进行回归，回归模型如下：

式（2）中，Sni表示投入的松弛变量，Zi为外部环境变量，βn是系数，νni+μni为误差项之和，νni为随机误差项，服从ν～N（0，σ2ν），μni为管理无效率项，假设其服从半正态分布，γ=μn2i（/μn2i+νn2i），当γ 接近于1 时，技术管理水平占主导地位，当γ 接近于0 时，随机因素占主导地位。紧接着对投入变量进行调整，调整公式如下：

式（3）中，XnA

i是调整后的投入值，Xni是原始投入值，两个括号内分别表示对环境因素和随机因素的调整。

3.第三阶段DEA

将调整后的投入变量与原始产出变量结合，再次运用投入导向的BCC 模型测算各省市真实的生态效率值。

三、生态效率测度指标体系构建与数据处理

（一）指标选取

1.投入产出指标的构建

生态是一个国家持续发展的基础，自然资源与社会资源是生态发展的必要元素，自然资源指标选取生态用水总量、建成区面积、能源消费量和电力消费量，社会资源指标选取年末从业人员数、固定资产投资和地方财政环境保护支出。环境投入是生态的非期望产出，我们将其作为生态投入，选择废水、废气排放量及一般工业固体废物产生量来表征，经济发展是生态的期望产出，用地区生产总值来衡量，现有文献测度生态效率方法较多，考虑到投入指标数量过多可能会产生测度偏差，因此，本文借鉴龙亮军[11]对生态绩效指标的构建方法，在衡量生态效率几个单一指标基础上，采用主成分分析法构造环境投入综合指标和自然资源投入综合指标，并在其基础上增加社会资源投入综合指标。

2.SFA 模型环境变量的选取

环境变量的选取应遵循对生态效率产生影响但又不受各省市自主控制的原则。城镇化率即城镇人口与该地区年末常驻人口的占比，由于农村人口与城镇人口相对数量的变化会影响资源要素的配置结构，且新型城镇化发展的内涵与生态文明理念相契合，因此,探究城镇化对生态发展的影响极具现实意义。产业结构用各省市第三产业增加值与该省市的生产总值之比表示，第三产业的发展是衡量我国生产力发展水平的标准，产业结构的调整已然成为影响我国资源、环境和经济效益的主要因素。研发强度为研究与试验发展经费内部支出与各地区生产总值之比，科技研发是强国的重要支撑，合理的研发强度能够降低污染物排放强度、提高资源使用效率，如何通过科技创新打造研发“生态圈”是当前生态与经济发展的热点问题。

（二）数据的处理

1.pearson 相关系数检验

为了满足DEA 模型中投入产出指标同向性的要求，对2011—2017年各省市投入、产出指标的平均水平进行pearson 相关系数检验，结果为在投入变量中除了一般工业固体废物产生量与生态用水总量，其余指标相关系数较大且均在1%的统计水平下显著，因此剔除一般工业固体废物产生量与生态用水总量这两个指标。数据主要来源于中国统计年鉴及各省市统计年鉴。

2.PCA 降维

分别对环境投入、自然资源投入和社会资源投入指标进行主成分分析，由于篇幅原因，此处以自然资源投入指标为例进行说明。主成分分析显示，KMO 值为0.754> 0.7，p 值为0.000，表明主成分分析可以有效地提取综合指标，同时第一主成分贡献率达到了92.2%，大于85%，因此这一主成分可以作为自然资源投入综合指标带入DEA 模型。

3.归一化处理

为了使数据趋于平滑且满足DEA 模型对数据为正值的要求，在主成分得分的基础上采用极差变化法对数据进行归一化处理，使其处于[0.1，1]之间，处理公式如下：

四、我国区域生态效率测度

（一）第一阶段DEA 测度

把中国30 个省、市、自治区（未包含西藏、香港、澳门、台湾）2011—2017年间的投入产出数据代入DEAP2.1 软件，得到各省市的技术效率、纯技术效率和规模效率。限于篇幅以及数据统计等原因，本文仅列出30 个省市在2011—2017年间的平均效率值（见表1）。

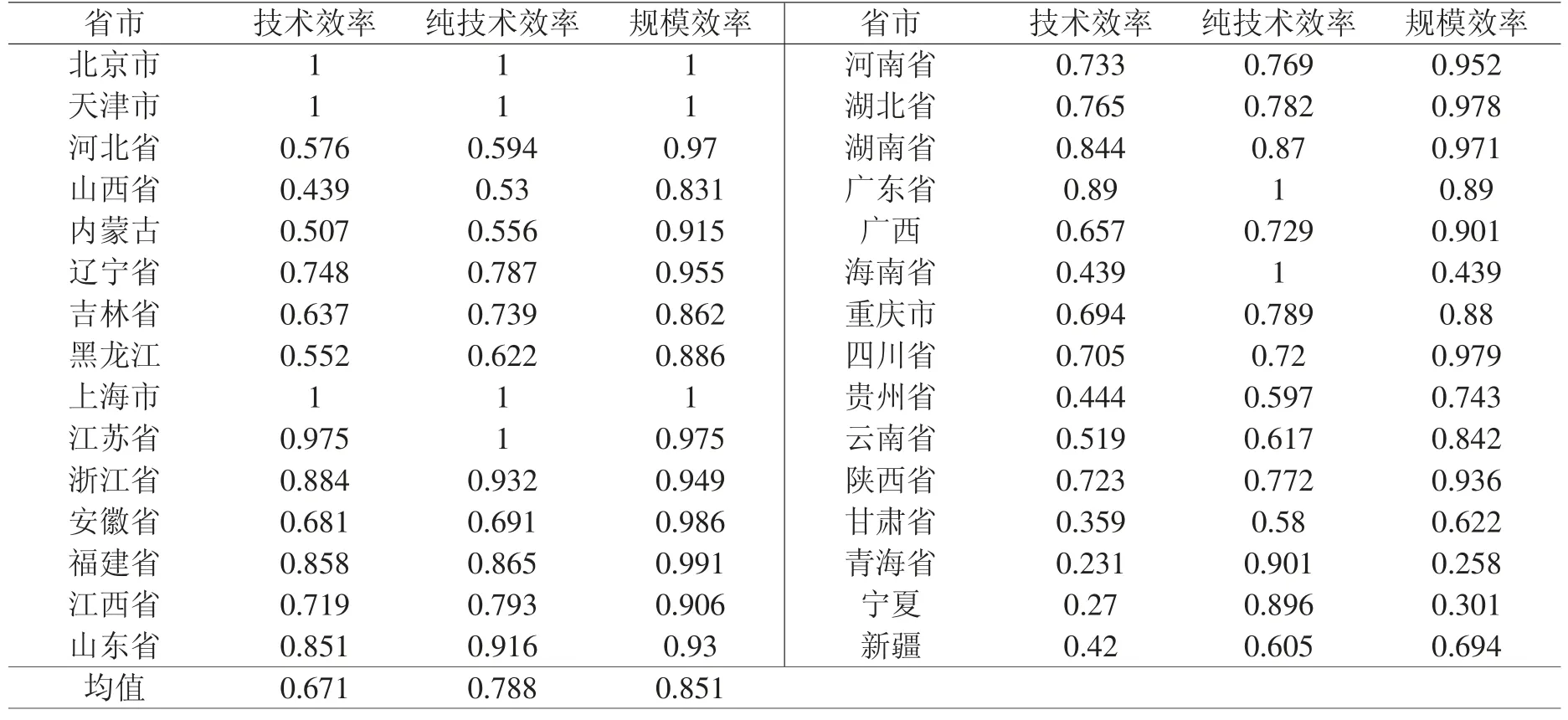
表1 第一阶段2011—2017年间平均效率值

表1 显示，我国省域技术效率均值为0.671、其整体生态效率值偏低，由纯技术效率为0.788，规模效率为0.851，且技术效率=纯技术效率×规模效率，可知纯技术效率不足成为制约我国生态发展的主要因素。分析各个省市的生态效率值，北京、天津和上海的效率值均为1，处于效率前沿面，说明其资源投入效率高，生态效率发展态势良好，属于生态效率发展中的佼佼者。江苏、广东和海南这3 个省份的纯技术效率为1，但其技术效率和规模效率均小于1，说明其偏离效率前沿面是由规模效率引起的。其余省份的三个效率值均小于1，说明投入产出没有达到合理的状态，资源利用效率较低且生态环境保护较差，导致总体的生态效益较差。以上分析结果受环境因素和随机因素的影响，不能真实地反映我国各省市的生态效率值，因此对投入要素进行调整测度真实效率值。

（二）第二阶段DEA 测度

为了消除环境因素与随机因素的干扰，运用Frontier4.1 将环境投入松弛变量、自然资源投入松弛变量和社会资源投入松弛变量对环境变量进行SFA 回归，结果见表3，回归系数较小是因为本文对投入数据进行了主成分分析，同时环境变量没有进行标准化，但这并不影响SFA 回归效果。回归系数的T 检验值大都显著，说明环境变量对投入要素的松弛变量产生了较大的影响。三个回归方程的γ 值均大于0.9，且在1%水平下显著，说明在影响生态效率的因素中，管理因素占据主导地位。同时三个SFA 模型的LR 值大于1%显著性水平下的混合卡方分布临界值，即确定了无效率项的存在，因此进行SFA 回归并对投入要素进行调整是合理且有必要的，下面对SFA 回归结果进行具体分析。

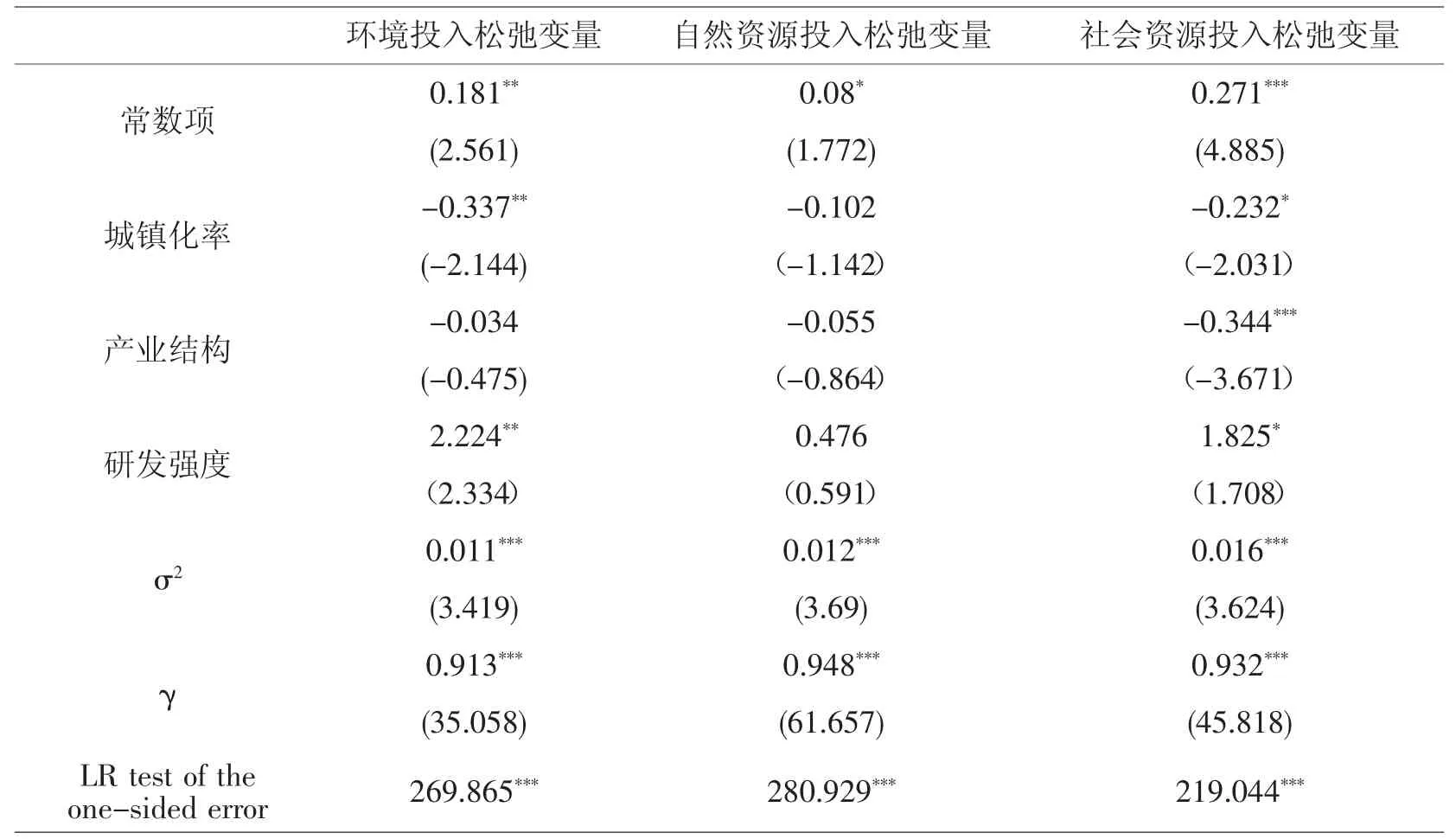
表2 SFA 回归

由表2 结果可知，回归系数有正有负，正负显现的投入产出效果相反，当回归系数大于零时，环境变量的增加会致使一部分投入要素无法转化为产出，不利于生态经济建设，当回归系数小于零时，环境变量对生态发展具有积极驱动作用，贡献于生态效率。

1.城镇化率。该环境变量对环境投入松弛变量、自然资源投入松弛变量和社会资源投入松弛变量的系数均为负，且分别对环境投入松弛变量、社会资源投入松弛变量系数在5%、10%的水平上显著，表明城镇化与生态环境建设正趋于协调发展的方向，城镇化能够显著优化生态环境和资源投入结构，虽然城镇化进程中人口空间的集聚会造成生态压力，但近年来政府积极健全环保机制，同时注重劳动力质量的提升和科技创新，已然形成城镇化与生态发展的良性互动机制。

2.产业结构。该环境变量对环境投入松弛变量、自然资源投入松弛变量和社会资源投入松弛变量的系数均为负，说明第三产业的发展会有助于实现绿色经济，原因是近年来流通业和服务业以清洁生产为理念，并以科技创新为依托推动产品由低附加值向高附加值的转变，同时政府不断加强绿色监管，健全绿色监督机制，最终在产业结构转型升级进程中带动了生态经济建设。然而产业结构只对社会资源投入松弛变量系数在1%的水平上显著，说明对社会资源投入变量影响显著，而对环境投入变量和自然资源投入变量影响较小，当增加第三产业占经济总量的占比，即产业结构的优化会大力推动人力、物力、财力等社会资源投入结构的优化，同时也会在一定程度上减少土地、能源等自然资源的消耗及废水、废气等污染物的排放，最终全面提高生态效率。

3.研发强度。该环境变量对环境投入松弛变量、自然资源投入松弛变量和社会资源投入松弛变量的系数均为正，且分别对环境投入松弛变量、社会资源投入松弛变量系数在5%、10%的水平上显著，理论上分析随着研发强度的增加，生产工艺更加先进，污染物排放和资源消耗都会随之减少，从而大幅度提高生态效率，但结果显示我国研发投入强度的增加并没有达到预期效果，盲目增加研发投入只会适得其反，导致资源浪费并降低生态效率，可能是研发投入强度的增加会提高发展成本，挤占其他活动所需的资源空间，导致整体生态效率值偏低。

（三）第三阶段DEA 测度

在第二阶段SFA 中剔除了环境因素与随机误差的干扰后，将调整后的投入与原产出代入DEA 模型中，得到中国30 个省市的真实效率值。同样，由于篇幅以及数据统计等原因，本文只列出30 个省市的平均效率值（见表3）。

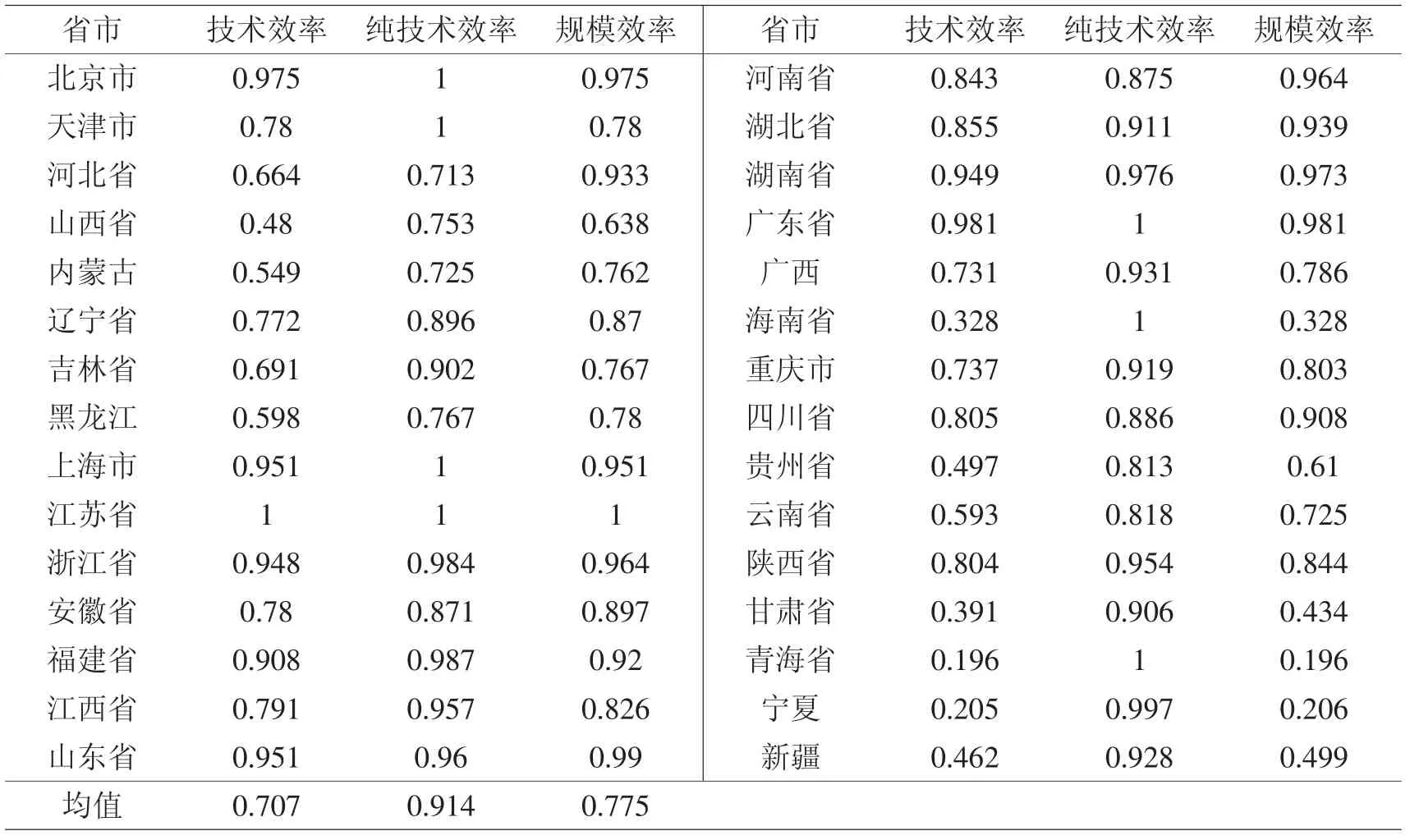
表3 第三阶段2011—2017年间平均效率值

由表3 可知，从我国整体效率来看，技术效率均值由第一阶段的0.671 上升为0.707，纯技术效率由0.788 上升为0.914，规模效率由0.851下降为0.755，说明实际上规模效率不足才是制约我国生态发展的主要因素。虽然消除环境因素与随机误差的影响后技术效率有所上升，但仍有29.3%的上升空间，所以全面提高生态效率刻不容缓。

从效率前沿面来看，第一阶段处于效率最优的有北京、天津和上海3 个城市，与之相比，便为仅有江苏省处于生态效率最优值，表明北京、天津和上海的生态效率最优包含了外部环境优势与随机运气，并不是真实地拥有较高的技术管理能力，而江苏省才是在技术管理因素方面占据真正的主导地位。从生态技术效率来看，下降的省市有北京、天津、上海、海南、青海和宁夏，这些省份效率值被高估与其所处的环境和随机因素有关。其余24 个省市的生态效率值表现出上升趋势，表明这些省市并非第一阶段DEA 中显示的生态效率值偏低。

（四）区域生态效率特征刻画

基于第三阶段DEA 得到调整后的效率值，运用R 软件画出以0.9 为临界值的空间集聚分布图（见图1），将我国各省市的生态效率分为四种类型：一是“高高型”，即纯技术效率和规模效率均大于0.9，如北京、上海、福建、浙江、江苏、山东、湖北、湖南和广东这9 个省市，较高的纯技术效率和规模效率提升了技术效率，属于我国生态效率发展中的佼佼者，因此，其在争取实现效率最优的同时要结合自身优势带动周边省市生态效率的发展。二是“高低型”，即纯技术效率大于0.9，规模效率小于0.9，如天津、吉林、重庆、广西、江西、海南、陕西、青海、新疆、甘肃和宁夏这11 个省市，这些省市技术效率偏低是由于规模效率引起的，因此，要适当调整生产规模，大力发挥规模集聚效应。三是“低高型”，即纯技术效率小于0.9，规模效率大于0.9，如河北、河南和四川这3 省，其技术效率偏低是由纯技术效率造成的，因此，要大力提高技术管理水平，使纯技术效率与规模效率实现平衡稳步增长。四是“低低型”，即纯技术效率和规模效率都小于0.9，如山西、黑龙江、安徽、内蒙古、辽宁、贵州、云南这7 省，其纯技术效率和规模效率均有很大的改进空间，因此，国家应注重对这些地区的生态扶持，各省市亦应加强自身生态建设，争取早日由“低低型”转为“高高型”。

五、简要结论与建议

文章采用PCA—三阶段DEA 组合模型测算2011—2017年间我国省域的生态效率值，得出以下结论与建议。

（1）对比剔除环境因素与随机因素影响前后的第一阶段、第三阶段生态效率值，发现我国整体技术效率与纯技术效率均出现上升，规模效率显现下降，表明我国生态技术效率受规模效率影响较大。可能由于我国长期沿袭粗放型的生产经营方式，生产规模不合理，无法发挥企业规模集聚效应，因此,国家应给予规模经营一定的资金支持和政策优惠，鼓励生产规模低下的企业进行重组、合并，创造规模经营的平台，同时要激励企业创新生产，提高企业核心技术水平并最终提升企业的市场竞争力。

（2）在外部环境对生态效率的影响中，提高城镇化率有利于生态发展，因此，要不断推动城镇化发展，保障农村就业人口向城镇就业人口转变的数量与质量，提高资源使用效率，保护生态环境。产业结构对各投入松弛变量的系数均为负，说明第三产业占比越大，生态效率越高，因此，应该大力发展第三产业，加速产业结构的转型升级，扩大就业，杜绝资源浪费，形成生态安全与经济协调发展的美好格局。研发强度对各投入松弛变量的系数均为正，表明增加研发强度并没有达到预期效果，因此，我国在鼓励科技创新的同时，要有针对性地进行研发投入，合理配置研发资源，形成科技创新引领发展并美化生态的良好态势。

（3）以0.9 为临界值，将30 个省市生态效率的空间格局分为四类，处于“高高型”的省市应该基于自身发展要求，进一步提升生态效率，争取早日达到效率前沿面，并积极带动周边城市生态效率的发展。处于“高低型”的省市要适当调整生产规模，提高规模效率。处于“低高型”的省市要注重改善纯技术效率，不断提升自身的技术管理水平。处于“低低型”的省市要同时提升纯技术效率与规模效率，不断实现技术效率的稳步提升。