基于标签进行度量学习的图半监督学习算法

吕亚丽，苗钧重，胡玮昕

（1.山西财经大学信息学院，太原 030006；2.计算智能与中文信息处理教育部重点实验室（山西大学），太原 030006）

（∗通信作者电子邮箱sxlvyali@126.com）

0 引言

随着机器学习算法的迅猛发展，其应用领域也越来越广泛，需要处理的数据也越来越复杂。由于标签数据有标准或最优的输出，所以在算法中可以很好地构建目标函数用于求解模型参数。然而，大数据环境下，标签信息有限，许多无标签数据唾手可得，但要想获得它们的标签信息却需要付出高昂的人工成本［1］。因此，如何同时利用少量标签数据与大量无标签数据提高模型的分类性能这一问题显得越来越重要。尤其是在学习过程中，如何降低模型学习对标签样本的需求量，同时又可以提高学习性能，成为了一个非常重要的研究问题［2-3］。近些年，涌现出大量关于半监督学习的研究工作并取得了较好效果［4］，其中包括较为热点的图半监督学习算法，其任务可以转换为一个凸优化问题，从而可以求得全局最优解［5］。

半监督学习算法大致可以分为直推式学习和归纳学习两类［4］。直推式学习是指根据标签数据推断数据集中无标签样本的类别的算法。归纳学习是指同时利用标签数据和无标签数据训练出一个分类器，再将其用于分类未知样本的算法。

基于图的半监督学习属于直推式学习的一种，是基于局部假设和全局假设来进行的，局部假设为邻近的样本应该具有相同的类标签［6］，全局假设是在同一结构中的样本应该具有相同的类标签。基于图的半监督学习可以总结为将数据中少数的标签进行传播，利用大量的无标签数据进行样本空间的结构识别［7］。

大多数基于图的半监督学习算法包含两个步骤：一是通过计算样本间的距离或相似性度量来构建相似度矩阵。每个样本可以看作是图中的一个节点，样本间的相似度可以看作是图中节点间连边的权重［8］。权重越大表示这两个样本具有相同标签的概率就越大。二是根据得出的相似度矩阵来预测无标签样本的所属类别。

目前，第一步已有工作在构建相似度矩阵方面的算法有：k-近邻（k-Nearest Neighbor，KNN）、ε近邻（ε-neighbor）［9］、热核方法（heat kernel）［10］、局部线性表示（local linear representation）［8，11］、低秩表示（Subspace Segmentation by Low Rank Representation，S2LRR）［12］以及稀疏表示（sparse representation）［13-15］等。其中，KNN方法在构建相似度矩阵时，选择距离每个样本点最近的k个样本点作为其邻居，据此构建样本间相似度矩阵。在该方法中，通常测量的是样本间的欧氏距离，超参数k的选择非常重要，k过大过小均不能正确反映出样本间的相似性。在ε-neighbor方法中，通过设定阈值来筛选对应样本的邻居来构建相似度矩阵，该方法中阈值的选择尤为重要。而heat kernel［10］、local linear representation［8，11］、low rank representation［12］以及sparse representation［13-15］这四种方法基本原理是通过不同的核方法来度量样本间相似性，对于不同的核方法，均涉及超参数，这些参数决定了模型复杂度从而决定样本间的相似性度量是否合适。此外，文献［16］基于非负矩阵分解与概念分解提出了一种基于数据表示的图半监督学习算法。然而，上述算法基本采用了欧氏距离作为样本间相似性度量的核心方法，且其度量方式相对固定，这样对于不同数据采用不同的度量灵活性和适应性相对较差。

第二步预测标签方面的标签传播算法有：高斯场与调和函数（Gaussian Fields and Harmonic Functions，GFHF）［17］、局部和全局一致性（Local and Global Consistency，LGC）方法［6］以及特殊标签传播（Special Label Propagation，SLP）算法［18］等。其中，GFHF 方法是利用高斯核来度量样本间的相似度，使用调和函数来进行标签传播，在调和函数中：对于标签数据，函数值为其标签值；对于无标签数据，函数值为标签其类别归属的权重平均值。这种方法的优点在于优化问题，具有良好的数学性质，且具有闭式解。LGC方法基于流形正则化思想，通过构造一个相对平滑的分类目标函数，来实现标签传播过程中尽可能使得处于同一类簇结构中的样本具有相同的标签。此外，文献［19］提出了一种基于流形的可解释性的图半监督学习算法；文献［20］从图形信号处理的角度考虑了标签传播，提出了一种广义标签传播算法。而这些标签传播算法的标签传播过程与第一阶段的样本相似性度量过程是分离的，且对于中间结果的利用不够充分。

基于上述问题，本文提出了基于标签进行度量学习的图半监督学习算法（Semi-Supervised Learning algorithm of graph based on label Metric Learning，ML-SSL）。具体地，将在构建相似度矩阵与标签传播过程中均充分利用宝贵的标签信息。同时，利用标签传播过程中的中间结果来不断更新相似性度量方式，通过不断迭代优化调整相似性度量与标签传播，进而提升标签预测性能，提高分类准确率。本文提出的算法不仅使得样本间相似性度量更加准确，而且充分利用中间结果大大降低了对标签数据的需求量。最后，通过实验验证了本文所提算法在标签数据占比极小的情况也可以取得较高的分类准确率。

1 预备知识

1.1 基于图的半监督学习算法

在基于图的半监督学习中，第一步计算样本间相似度时，已有工作经常采用高斯核函数来进行［17-18，21］，如样本xi与xj的相似度被定义为：

这种方法将样本间的欧氏距离视作样本间的相似度，其核心还是欧氏距离，这种度量方式并未用到宝贵的标签信息，这样不仅导致了标签信息的浪费，而且使得相似性度量不精确。

基于图的半监督学习算法在进行标签传播时采用的思想是：相似度大的样本应该具有相同的标签。通常会先构建标签向量，如某一任务中共有K个类别的数据，其中某一样本属于第m类，那么该样本所对应的标签向量为(0，0，…，1，…，0)，即向量中除第m个元素为1外，其余元素均为0，同时还规定标签向量中所有元素之和为1。可以把标签向量中每一个位置上的元素看成是对应样本属于某一类的概率，当两个样本间的相似度sij较大时，样本xi与xj所对应的标签向量应尽可能地相似，即其欧氏距离要尽可能小。也就是将每一个样本点看作图中的一个节点，样本间的相似度看作是节点间连边的权重。然后，找到最合适的切割方式把整个图分成K个子图，使得各个子图所包含的边的权重之和最大，同时使得被切割掉的边的权重之和最小。

1.2 度量学习

许多机器学习算法很大程度上依赖于样本间的度量方式，一个合适的度量方式不仅可以使得学习的结果更加准确，而且可以使得学习过程更加便捷。大多数算法采用了固定的度量方式，常见的度量方式有欧氏距离、曼哈顿距离、推土机距离、切比雪夫距离等。还有一些算法是首先在原始样本空间上进行特征选择，然后在特征空间上进行固定形式的距离度量。

那么，如何根据实际问题或面对不同的数据进行不同方式的度量？面对这一问题，研究者们提出了很多度量学习方法：大边界最近邻算法［22］、基于密度加权的大边界最近邻分类算法［23］、基于余弦距离的度量学习算法等。

许多度量学习方法中采用了马氏距离作为度量的函数形式，根据样本相似性计算具体的度量参数值。其度量公式被定义为：

其中，矩阵A满足半正定。当A为单位矩阵时，该距离就变成了欧氏距离。

接下来根据样本间的相似度来计算A矩阵［24］。设M为相似样本对集合，D为不相似样本对集合。按相似样本之间的距离应尽可能小的原则，构建如下优化问题：

约束条件是为了避免所有的数据都集中到一个点这种极端情况的出现。该问题为一个凸优化问题，可以求得全局最优解。

若采用拉格朗日对偶性进行求解，其时间复杂度为O(n6)，空间复杂度为O(n2)。上述问题也可被转化为如下等价问题［24］来求解：

此时，可以使用梯度下降法对目标函数进行求解。用迭代优化的方式来使得A满足约束条件。

具体的距离度量学习（Distance Metric Learning，DML）求解思路如算法1所示。

2 基于DML的图半监督学习方法

本文主要利用标签信息进行相似性的度量学习，进而提出基于标签进行度量学习的图半监督学习算法。因此，本章首先给定相似性度量方式，进而构建相似度矩阵；其次，基于该相似性矩阵进行标签传播；接着，基于信息熵确定前k个相对确定的样本标签；然后，再加入新学出的标签信息进行相似性度量学习；最后，构建相似性矩阵和标签传播等，如此迭代，直至学出所有标签信息。

2.1 相似度矩阵的构建

给定一个包含n个样本的数据集X={x1，x2，…，xl，xl+1，…，xn}，具体包含l个具有标签的数据和u=n-l个无标签数据。给定一个标签集Y={1，2，…，C}表示有C个类。其中xi∈Rd（i=1，2，…，n），这里d表示数据的维度。

为了构建相似度矩阵S={sij}n×n，定义样本xi与xj的相似度为：

从概率角度看，sij可看作是xi选择xj作为自己邻居的概率，若记pj|i=sij，则pj|i为以xi为中心、单位矩阵I为协方差矩阵的高斯分布的概率密度［25］。

2.2 基于相似度矩阵的标签传播

当确定了样本间的相似度矩阵后，接下来根据相似度矩阵进行标签传播，给每个样本xi一个标签向量fi，若i≤l，则：

即若样本xi属于第j类，则标签向量第j个元素为1，其余均为0。若i>l，则fi为零向量。根据相似度大的样本的标签向量应比相似度小的样本的标签向量更相似的原则，本文也将标签传播定义为下述的优化问题：

这个最优化问题与下述的问题等价［17］：

式中：F∈Rn×c，其第i行表示第i个样本的标签向量。为方便起见，定义F={Fl，Fu}，Fl表示标签数据所对应的标签矩阵，Fu表示无标签数据的标签矩阵，目标是求解Fu。LS=D-S为一个拉普拉斯矩阵，S为相似度矩阵，D为对角矩阵，其第i个对角元素Dii=∑jsij。

现对L矩阵进行分块：

对于样本xi的标签向量fi={pi1，pi2，…，piC}，其中pij可以看作xi属于第j类的概率，在标签传播过程中，样本的标签向量可以体现出样本所属类别的不确定性程度，用标签向量的熵来作为这种不确定性的度量，即：

熵值越小则说明所对应样本的所属类别更加明确。低熵值样本将在后续的标签传播过程中改进样本间的度量，使得传播更加准确。

2.3 迭代更新

在半监督标签传播过程中，每次从学出的标签中筛选出分类准确率高的前k个新标签样本，即前k个低熵样本信息，利用它们进行距离度量矩阵的更新，以此来进行下一轮标签传播。在此过程中，样本间相似性度量不断地向着更加准确的方向变化着。从另一方面考虑，不同的相似性度量方式体现了不同的样本结构的分布形式。如果样本的分布更加明确，算法的分类效果就会有大幅提升。本文正是基于这一点设计了迭代优化的算法不断加强样本空间的结构识别，从而提升学习效果。

2.4 算法描述

基于上述内容，本节给出了迭代优化的算法——基于标签进行度量学习的图半监督学习算法（ML-SSL），具体伪代码描述如算法2所示。

算法2 中，第2）～4）行是初始的各个量的计算，包括初始化距离度量矩阵A、相似样本对集合M、标签向量矩阵Fu以及计算无标签样本的熵值。接着，算法进行迭代优化，通过低熵值样本与距离度量矩阵的相互作用影响彼此。循环终止的条件可以是距离度量矩阵A收敛，此时说明样本间的相似度已达到了最佳稳定状态，也可以是根据实际情况设定迭代次数。

3 实验与结果分析

本章设计如下实验验证本文所提算法的可行性和分类性能。实验主要分为三部分：首先，详细分析k值的选取情况；然后，在人造数据集上进行分类性能验证与分析；最后，在真实数据集上进行对比分析和验证。本文采用的对比算法包括LGC、GFHF 和S2LRR 三种，这三种方法均为半监督学习领域的经典算法；然而，在算法执行中均未利用中间结果，且在样本间相似性度量时未用到标签信息。通过实验结果可以看出，本文算法具有很大的竞争优势。

3.1 实验环境与数据集

本文实验所用的硬件环境为：Windows 10，CPU 主频为2.00 GHz，运行内存为8 GB，CPU型号为AMD A8-6410。

本文采用的人造数据集为一个双月型数据集，该数据集有上下两个半圆形，分别表示由两个类组成。每类包含100个二维样本，其中每个样本由两个实数描述其特征。该数据集属于非凸型数据集。从算法的二维结果可以展示其对数据空间结构的识别能力，具体如图1所示。

图1 双月型数据集Fig.1 Two-moon dataset

采用的真实数据集有Breast、German、Ionosphere、Vote、Heart、Monkl 共6 个，全部来自于UCI。详细信息如表1所示。

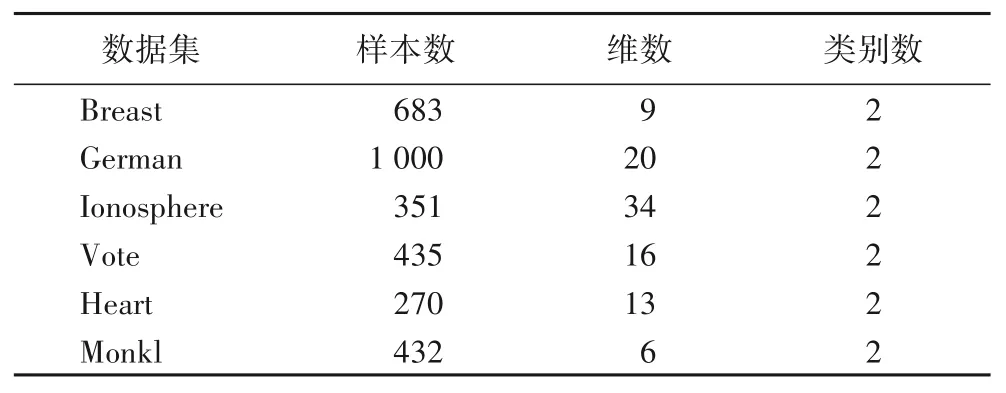
表1 来自于UCI的真实数据集Tab.1 Real datasets from UCI

3.2 度量指标和参数

实验采用分类准确率作为评价指标，即将数据集中无标签数据的真实标签yi与算法学习的预测标签i作比较，分类准确率acc为：

其中：Xu为无标签数据集；|Xu|为该集合所包含的样本量。

除了分类准确率外，还增加了一项标签样本占比的数据。实验通过这两项指标来说明本文所提算法在提高分类准确率方面的优势，从不同数据集的对比中可以体现所提算法的鲁棒性。

实验中，算法的参数设置为最大迭代次数n=20、判断度量矩阵A收敛的ε=0.01，即，则认为A收敛，设置低熵样本个数k=5。

3.3 k值对分类结果的影响

本文对k值的选择是通过在6 个真实数据集上进行交叉验证得出，具体是分别在每个数据集上随机分配12 个标签，然后分别取k=2、k=5、k=10 进行交叉验证，具体结果如表2所示。

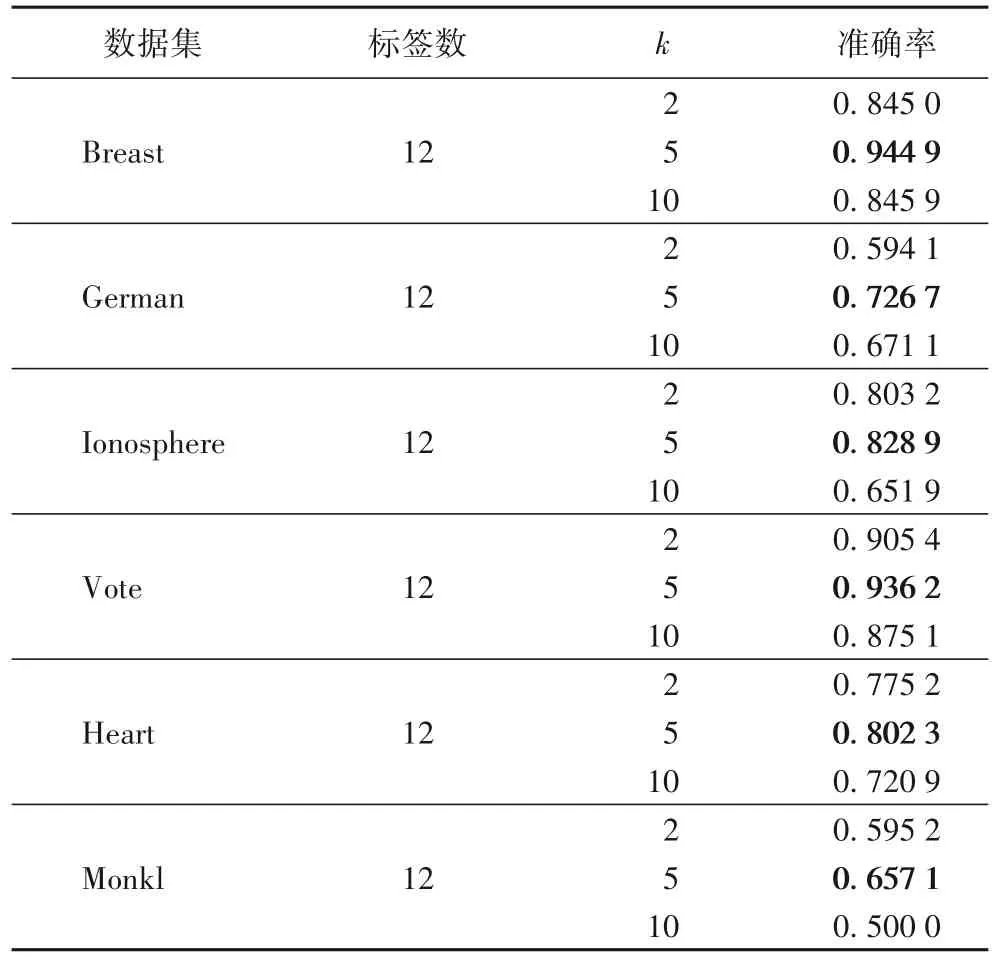
表2 交叉验证实验结果Tab.2 Experimental results of cross-validation

从表2 可以看出，当k=5 时分类效果最佳，具体见表中加粗部分。这是由于k的选择会对低熵值样本改进距离度量矩阵产生影响。具体地，当k=2，即取较小的值时，算法将会退化成固定度量方法，每次迭代所选出的确定性样本基本保持不变。当k=10，即取较大的值时，学习过程将会引入确定性较低的无标签样本，这样的样本对于距离度量矩阵的学习来说属于噪声影响。

3.4 人造数据集上的实验验证与分析

在人造数据集上，通过随机地为每类样本分配一定数量的标签来进行对比实验。这里分别随机地给每个类分配1、3、5、7、9 个标签，使用本文所提算法2 进行其余标签的学习。具体学习结果如图2～6 所示，每个图中子图（a）是初始数据集（initial data），图中正方形和倒三角分别表示两类标签数据点，圆形表示无标签数据点；子图（b）为运用所提算法2 的分类结果（result）。

图2 每类样本具有1个标签的分类结果Fig.2 Classification results of each class with one label

由图2～6可以得出：

1）本文所提算法在标签样本占比很小的情况下就可以得出较好的分类结果。

2）本文算法随标签样本数的增加分类效果明显增强，尤其是对每类数据尾部的样本分类，即从实验结果可以看出，分类错误的样本主要集中在每个类的尾部。随着标签样本数的提升，本文的算法加强了对尾部数据的分类能力。

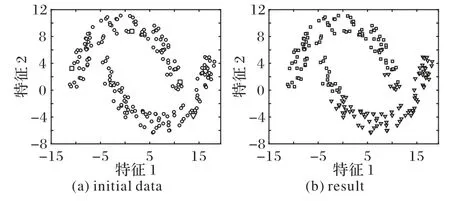
图3 每类样本具有3个标签的分类结果Fig.3 Classification results of each class with three labels

图4 每类样本具有5个标签的分类结果Fig.4 Classification results of each class with five labels

图5 每类样本具有7个标签的分类结果Fig.5 Classification results of each class with seven labels

图6 每类样本具有9个标签的分类结果Fig.6 Classification results of each class with nine labels

3.5 真实数据集上的实验及其结果分析

在6 个真实数据集上对本文算法（ML-SSL）进行实验验证，并与LGC［6］、GFHF［17］以及S2LRR［2］这3 种半监督学习算法进行实验对比。每个数据集上类别数为2，随机地给每个类分配2、4、6、8、10个标签，则每个数据集分别分配4、8、12、16、20。4 种算法在不同数据集、不同标签数下的分类结果具体如表3 所示。其中，粗体表示每种情况下取得的最高分类准确率。

另外，随着标签样本数的增加，4 种算法取得的分类准确率变化如图7 所示，子图（a）～（f）分别代表Breast、German、Ionosphere、Vote、Heart以及Monkl数据集上二者间的关系。

图7 不同数据集上标签数量与不同算法分类准确率的关系Fig.7 Relationship between number of labels and classification accuracy of different algorithms on different datasets

表3 真实数据集上的分类准确率Tab.3 Classification accuracy on real datasets

由表3和图7可以得出：

1）除German 数据集上已知标签数是4 的情况外，其余情况下本文所提算法均取得了最高的分类准确率，即本文所提算法在6 个数据集上准确率最高的情况占比达到96.7%（29/30）。具体的，在Breast数据上，本文算法相较其他3种算法在准确率上平均提高了16.72 个百分点；在German 数据集上提高了14.79 个百分点；在Ionosphere 数据集上提高了11.84 个百分点；在Vote 数据集上提高了26.37 个百分点；在Heart 数据集上提高了16.55 个百分点；在Monkl 数据集上提高了9.62 个百分点。由此可见，本文所提算法在绝大多数情况下的分类准确率均优于其他3种算法。

2）每个数据集上已知标签比例范围为［0.001 7，0.074 1］，可见本文所提算法在已知标签比例很低的情况下便可取得相较于其他3 种算法更高的分类准确率。在Breast数据集上当标签数为20、标签占比仅为0.029 3 时，分类准确率达到了0.965 3；在German 数据集中，最高分类准确率达到了0.731 6，此时标签占比仅为0.02；在Vote 数据集中，在标签占比仅为0.009 2 即不到1%的情况下，本文所提算法的分类准确率达到了0.874 7。从上述分析可知，在标签数极少的情况下，本文所提算法也能实现较高准确率的分类效果。

3）从图7 的子图（a）、（c）、（e）、（f）可以看出，本文所提算法在Breast 数据集、Ionosphere 数据集、Heart 数据集以及Monkl 数据集上的分类准确率随标签数的增加而增加。而其他3 种半监督学习算法，分类准确率并不随着标签数的增加而直线提高，尤其S2LRR 算法，起伏很大。在German 数据集和Vote 数据集上，通过对比4 种算法所对应的曲线也可以明显看出，本文所提算法比其他3 个算法更加平稳，表明了本文算法具有较好的鲁棒性。

4 结语

为更准确地反映样本间相似性关系以及充分利用中间结果来提高半监督学习的分类准确率，本文提出了一种基于标签进行度量学习的图半监督学习算法，利用标签传播过程中确定性标签样本来不断修正样本间的相似性度量方式。然后，通过迭代算法使得以样本为节点、相似度为边权重的图不断得以优化，从而使得标签传播更加准确，并通过实验验证了所提算法的良好分类性能。接下来，我们进一步的研究工作包括该算法的合理性理论分析、计算效率的提高、算法中参数k的选取方法以及该算法的实际应用研究等方面。