Φ273管道的电磁励磁仿真模型分析与实验方法*

杨理践， 徐 龙， 高松巍

(沈阳工业大学 信息科学与工程学院， 沈阳 110870)

当今世界能源运输愈发重要，油气管道作为一种特殊载体对于长距离运输石油、天然气等重要能源物资具有无法替代的作用.漏磁检测作为无损检测技术的一种，被广泛应用于长输油气管道缺陷在线检测[1]，对于在役油气管道的金属缺陷及裂纹异常检测具有一定的效果[2]，该技术突出优势在于效率高、可靠性高及检测成本较低.

随着科技的逐渐发展，漏磁检测技术日趋成熟.日本学者Nara等[3]实现对管道缺陷的精确识别，并研究漏磁信号从时域到频域的过程；韩国学者Hui等[4]在三维轴向裂纹的研究分析中采用了有限元的方法；冯健等[5]提出了基于神经网络的漏磁信号模式识别技术；黄作英等[6]应用磁荷法确定漏磁信号的数学模型；彭丽莎等[7]对管道缺陷重构方法进行研究；杨理践等[8-10]以工程应用中的管道漏磁检测系统为基础，研究漏磁场缺陷信号的各种特征，并尝试将剩磁效应应用在管道检测中，分析了漏磁检测信号的影响因素及永磁励磁的磁路优化.

本文提出了一种适用于管道漏磁内检测技术的电磁励磁方式，依据永磁体模型参数及产生磁场特点探求具有相同磁化效果的电磁励磁磁路模型，对比分析管道缺陷在不同磁路特征下所表现的特性，并构建仿真模型与实验数据之间的关系，从而建立准确的磁回路仿真模型.

1 油气管道漏磁内检测技术

长输油气管道一般由高磁导率的铁磁性材料加工而成，检测之前需要经励磁装置磁化，磁化主要包括电磁励磁和永磁励磁两种，它们产生能量的方式不同，磁路结构也存在一定区别，需要根据实际情况做出合适的选择.

1.1 永磁励磁的磁路模型

永磁励磁方式在漏磁检测中应用较为广泛，在无缺陷时，磁感应线会在管道内部平行且均匀通过，理想情况下泄露的磁通量基本为零；当表面或近表面存在缺陷时，磁感应线受到阻隔发生畸变，部分磁感应线会泄露到空气中，产生的漏磁通会形成漏磁场，其检测基本模型如图1所示.

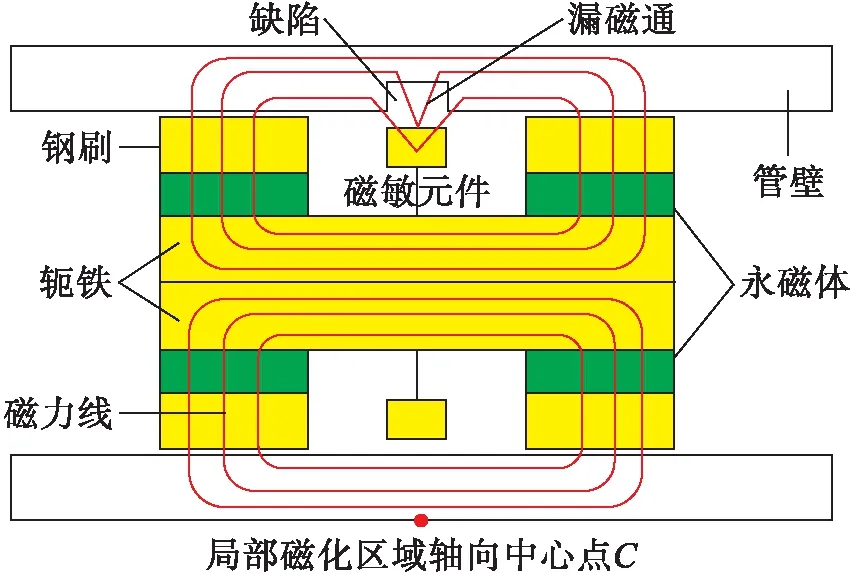
图1 永磁磁励的磁路模型Fig.1 Magnetic circuit model for permanent magnetic excitation

1.2 电磁励磁的磁路模型

以永磁励磁模型为基础，铁芯上绕制匝数为N、激励电流为I的线圈，通过调整参数实现最佳磁化效果，磁路模型如图2所示.

图2 电磁励磁的磁路模型Fig.2 Magnetic circuit model for electromagnetic excitation

电磁励磁的磁路有两部分，由于模型完全对称，可认为两个部分的磁回路均分能量.取其中一个磁路，由铁芯、钢刷、轭铁和气隙串联而成.

磁路计算时，通常将磁路分为两部分：一部分为铁芯，截面积为Sm，长度为Lm，磁场强度为Hm，磁感应强度为Bm；另一部分为气隙，截面积为Sδ，长度为Lδ，磁场强度和磁感应强度分别用Hδ、Bδ来表示.

根据安培环路定理可知

F=HmLm+HδLδ=IN

(1)

式中，F为整个电磁铁的磁通势.

根据所建立的磁路模型，可以求得该磁路的磁通Φ为

(2)

式中：Rδ为气隙磁阻；R1为导磁材料磁阻；R2为管道磁阻.若仅考虑气隙磁阻，则

(3)

将式(2)改写为

(4)

式中：μ0为空气磁导率；w为磁路的宽度；h为磁路径向有效长度.

气隙的磁感应强度Bδ为

(5)

由式(5)可知：影响磁路气隙磁感应强度的主要因素不但包括线圈的匝数、电流值的大小，还有气隙长度.

管壁截面处的磁感应强度为

(6)

由安培环路定理得电磁铁的磁感应强度为

(7)

当电磁铁几何参数固定时，管道中某一点的磁感应强度大小与线圈匝数、激励电流具有密切关系，为建立仿真分析提供了理论基础.

2 电磁场磁路分析

在实际工程应用中，电磁场中偏微分方程的求解是一个极其复杂的过程，并且只有少数的场问题能够得到解析解，需要使用其他的计算方式来进行求解.

2.1 漏磁场计算的数值法

对于电流密度J在磁导率为μ的介质中所形成的磁场强度与磁感应强度的关系，可由磁通连续性原理与全电流定律获得，即

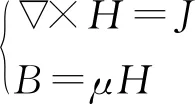
(8)

由于磁感应强度法向连续，磁场强度切向连续，引入磁位A为

×A=B

(9)

理想管道结构周向完全对称，矢量磁位只有一个分量，则控制方程为

(10)

采用柱坐标系进行分析可知

(11)

可以求得磁感应强度为

(12)

(13)

式中：r为径向参数；Br为磁感应径向分量；Bz为磁感应轴向分量.

2.2 三维有限元分析方法

有限元分析的基本思想是利用离散化数值求解，由麦克斯韦方程组推导出磁场的偏微分方程为

(14)

式中，ε为介电常数.引入的矢量磁势满足

(15)

利用变分法将三维静态磁场用标量形式泛函表示得

(16)

式中，P为中间量，其值为

P=AxJx+AyJy+AzJz

(17)

对式(17)进行离散分析，磁位A转换为直角坐标系并引入x，y，z三个分量，对磁位求偏导，化简为

(18)

式中：K为刚度矩阵；f为激励.

3 电磁励磁模型有限元仿真

建立Φ273(壁厚约为6.8 mm)管道电磁励磁模型，分析管道在达到近饱和状态下线圈匝数及激励电流参数，并分析缺陷特性.模型的具体几何尺寸如表1所示.

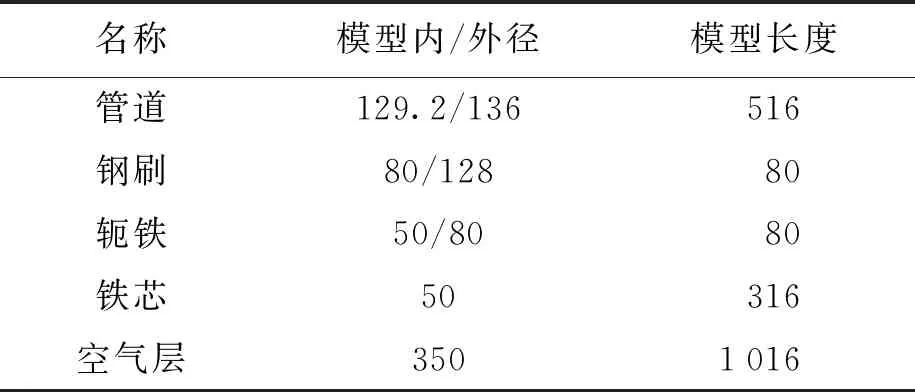
表1 电磁励磁仿真模型各部分几何尺寸Tab.1 Geometry of various parts of electromagnetic excitation simulation model mm

3.1 COMSOL有限元仿真软件及仿真流程

COMSOL是一款应用广泛的高级数值仿真软件，优势在于多物理场耦合，本文主要以有限元法为基础，通过对偏微分方程的求解来实现真实物理现象的仿真.几何建模后，由于模型中各部分的材料功能不同，部分材料属性需要自定义.

管道选用X52钢，轭铁选用Q235钢，是一种普通碳素结构钢，屈服值大约为235 MPa，综合性能较为优越，应用范围广泛.对于钢刷的介质描述十分困难，磁特性接近线性，本文设定磁导率为7.需要注意的是，上述的几种材料均为各向同性.

网格划分的形状和疏密程度将会在很大程度上影响最后的计算结果，本文采用智能网格划分方式，对于管道还需要进行局部网格细化.

软件会自动将模型电磁铁电流加载到模型上，不需要施加其他载荷.此外，空气层要达到一定程度来模拟远场边界的约束条件.经过稳态求解器计算，利用软件提供的结果通用处理器可以查看磁通密度分布云图、磁感应图、磁场等值图及各种矢量图.

3.2 模型参数优化

电磁励磁模型中的参数包括线圈匝数、激励电流大小、线径以及线圈的体积等，它们都会对产生的磁化能量有着或多或少的影响，在设计和使用时需要调整.已知无缺陷管道外壁点C处磁通密度约为10 mT，以此为基准进行参数优化，考虑到激励电流不宜过大(这里选用0.3 A的激励电流)，不同线圈匝数模型所表现出来的磁通密度分布云图如图3所示.

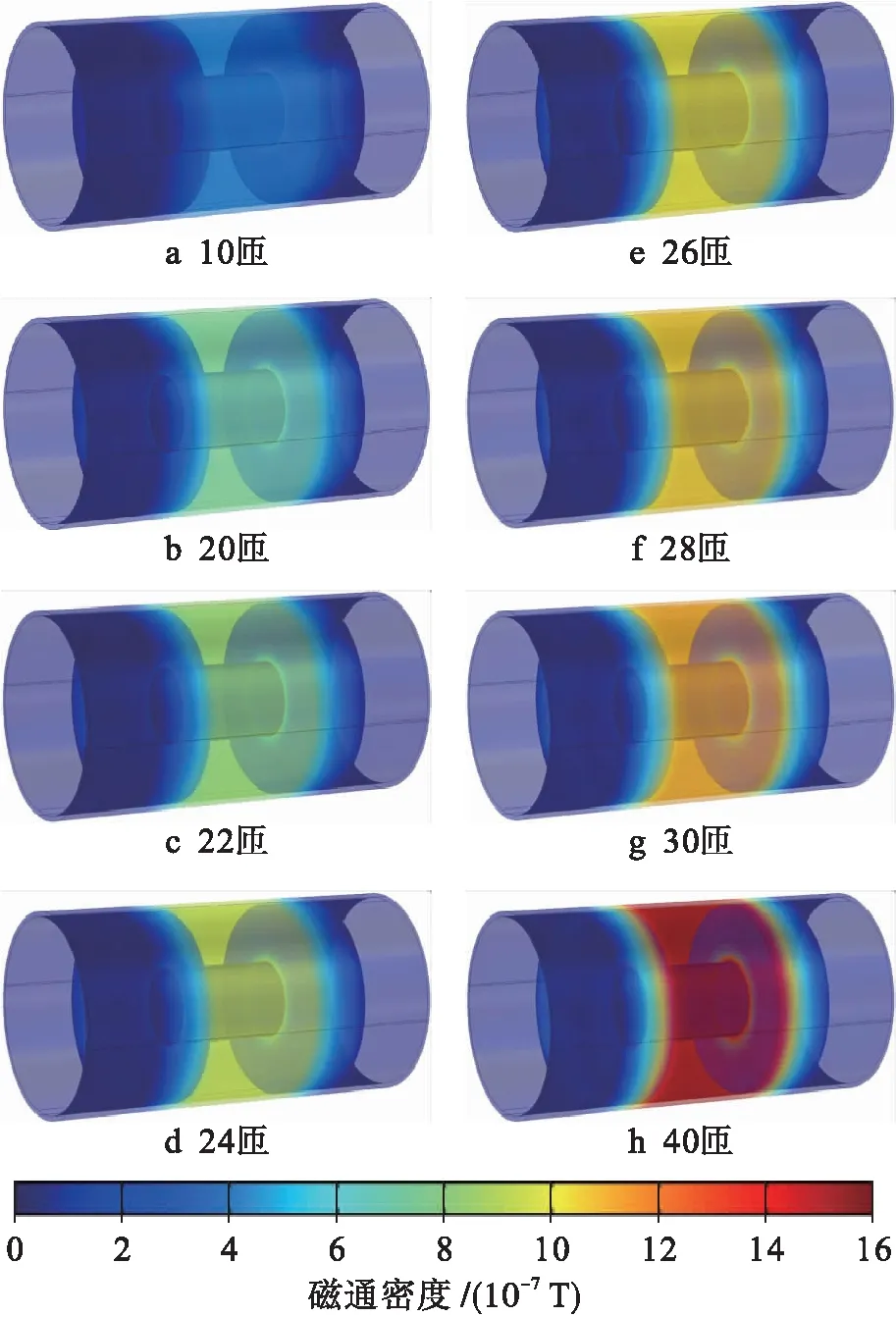
图3 不同线圈的仿真模型磁通密度云图Fig.3 Magnetic flux density nephogram of simulation model for different coils

由图3可知：随着线圈匝数的增加，管道中间的局部磁化区域能量逐渐增强.当线圈匝数少于20匝时，管道的磁化程度未达到要求；当线圈匝数超过30匝时，管道达到过饱和状态，不符合实际中的检测要求.选取其中线圈匝数为20～28匝的模型，通过路径映射的方式测量管道外壁轴向磁通分量的具体数值，测量结果如图4所示.

仿真结果分析可知：随着电磁铁中线圈匝数增加，C点处轴向磁通分量会逐渐变大.当电磁铁中的线圈匝数接近26匝时，轴向磁通分量为10.046 mT，误差为4.6%.

3.3 不同径向深度缺陷特性分析

在电磁励磁模型中，线圈匝数为26匝，激励电流为0.3 A，选用轴向长度为40 mm、周向宽度为20 mm、径向深度分别为1.3、1.8、2.4、4.0 mm的缺陷进行分析，不同径向深度缺陷的径向磁通分量曲线如图5所示.

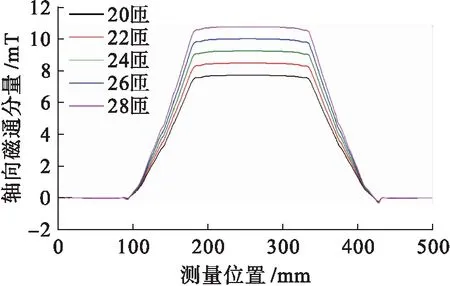
图4 不同线圈匝数下C点的轴向磁通分量Fig.4 Axial flux component at point C under different coil turns

图5 不同径向深度缺陷的径向磁通分量Fig.5 Radial flux components of defects with different radical depths

由图5可见，在缺陷的中心处位置，径向磁通分量数值较小，接近于零；在缺陷的两侧边缘位置，径向磁通分量会达到峰值点；随着缺陷的径向深度增加，径向分量的峰值逐渐变大，峰值随缺陷径向深度增加分别为0.013 3、0.013 5、0.014 4、0.021 9 mT.

3.4 不同轴向长度缺陷特性分析

选用周向宽度为40 mm、径向深度为1.8 mm、轴向长度分别为10、20、40 mm的缺陷进行分析，径向磁通分量曲线如图6所示.

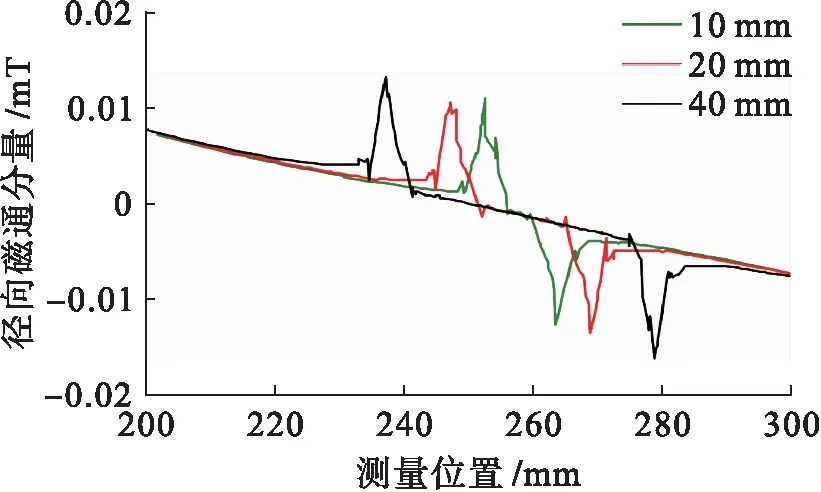
图6 不同轴向长度缺陷的径向磁通分量Fig.6 Radial flux components of defects with different axial lengths

由图6可见，随着缺陷长度增加，径向分量的峰峰值间距增大；在缺陷的中心位置，径向分量接近于零；在缺陷的边缘位置，由于磁力线集中，径向分量会达到峰值.

4 实验与结果分析

根据工程中漏磁内检测装置所检测的结果，研究不同磁路特征的漏磁信号曲线特性及磁感应强度分布特点，探求工程实验与电磁铁仿真之间的联系与区别.

4.1 实验装置

采用Φ273管道漏磁检测装置进行拖拉实验，其中漏磁内检测装置在管道中运行，主要分为动力节、磁化节(参数与电磁励磁仿真模型完全相同)、计算机节和电池节，各部分协同工作.实验装置的结构如图7所示.检测装置中磁敏探头元件为包含数字输出的三轴霍尔传感器MLX90393，可以检测到1 050 mT的磁场强度.

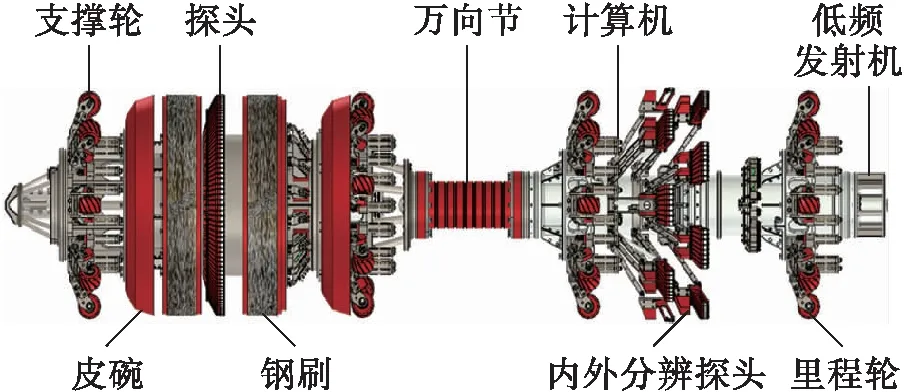
图7 管道漏磁内检测器结构Fig.7 Structure of internal detector for pipeline magnetic flux leakage

4.2 实验结果

检测到的漏磁场信号被存储到计算机节进行初步处理，待拖拉实验结束后，将数据导入专用上位机软件，得到轴向凹沟3个探头所采集的径向磁通密度数据，如图8所示，每条曲线代表一个探头的数据.

由图8可见，随着深度的增加，径向磁通分量峰值逐渐变大，验证了仿真结果的形态趋势.深度为1.3、1.8、2.4、4.0 mm时，3个探头峰值均值分别为2.38、3.28、4.62、8.33 mT.从峰值的均值数据上可以看出：经归一化深度每增加0.1 mm，其径向磁通分量的峰值增加约0.16 mT，呈线性关系.

综上所述，永磁励磁实验装置与电磁励磁仿真模型在不同磁路特征下表现出相同的磁路特性，验证了以电磁励磁模型替代永磁励磁模型进行分析的有效性，证明电磁励磁仿真模型对永磁磁路优化具有指导意义.

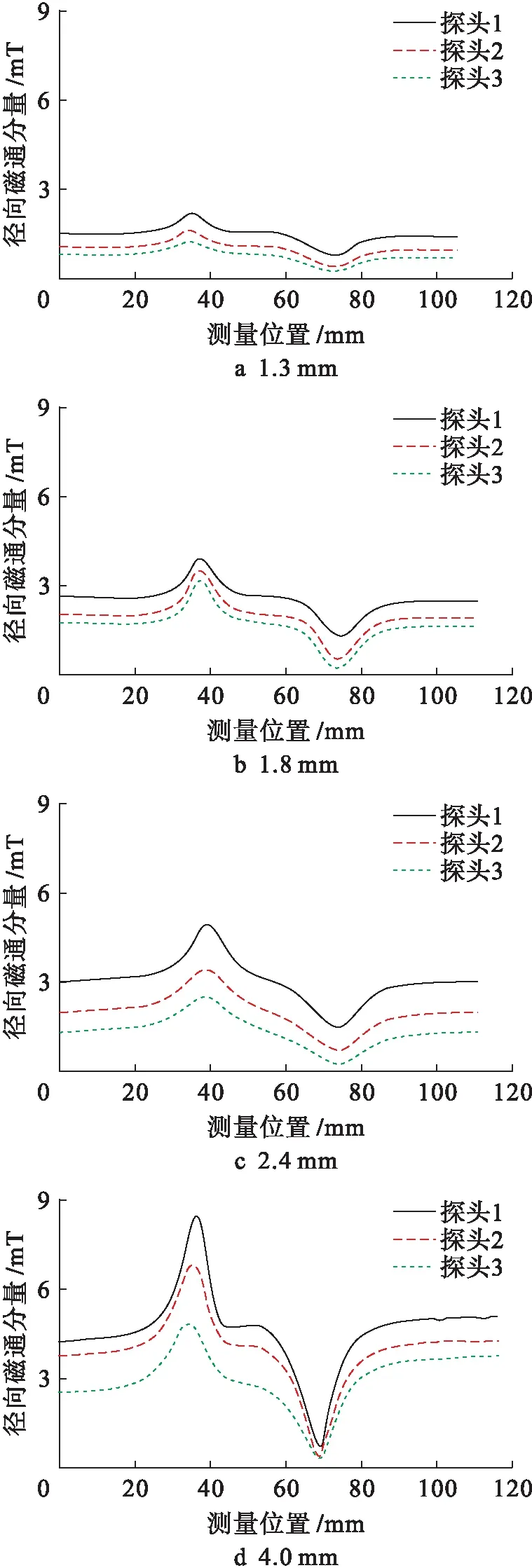
图8 不同深度缺陷的径向磁通数据曲线Fig.8 Radial magnetic flux data curves of defects with different depths

5 结 论

通过仿真与实验的对比分析，结合工程电磁场理论，得出以下结论：

1) 相同模型尺寸下，调整电磁铁参数可使电磁励磁与永磁励磁具有相同的磁化效果.

2) 电磁励磁对于不同磁路特征所表现出来的特性具有相同的形态趋势，证明了从电磁场角度来分析永磁磁路的可行性.

3) 由理论计算得知：电磁励磁仿真结果与工程中永磁励磁结果之间存在线性比例关系，说明可以从电磁场角度建立准确的漏磁检测仿真模型.