考虑爆破效应的隧道开挖损伤区及渗流场分析*

许梦飞， 姜谙男， 蒋腾飞， 申发义， 白 涛

(1. 大连海事大学 道路与桥梁工程研究所， 辽宁 大连 116026； 2. 吉林省高速公路集团有限公司， 长春 130000； 3. 吉林省交通规划设计院， 长春 130000)

随着隧道工程的蓬勃发展，围岩稳定性评价问题成为了岩土工程界的研究热点.隧道开挖面附近的岩石，其力学性质和渗透特性在开挖扰动和地应力重分布的影响下会发生变化，形成开挖损伤区.开挖损伤区附近的围岩力学参数与地勘、设计给出的初始参数相比会发生较大程度的弱化，渗透系数会成几个数量级的增加，若仍从设计参数出发进行围岩稳定性评价，势必会造成工程隐患.因此，采用合理的方法预测开挖损伤区对隧道施工设计和洞内涌水量控制有着重要意义.Diederichs[1]对深部地下工程中岩石碎裂及产生岩爆的判定依据进行了讨论，并建立了数值计算模型，对深埋盾构开挖破坏半径进行了预测，取得了良好效果；Perras等[2]在Diederichs研究基础上，采用不同预测方程对高度损伤区、内部损伤区和外部损伤区范围进行了数值模拟；王军祥等[3]利用ABAQUS软件对隧道围岩稳定性的影响因素进行了分析；Harrison等[4]指出开挖损伤区由两部分组成，一是开挖手段造成的岩石初始不可逆损伤；二是后期支护过程中应力重分布造成的损伤；严鹏等[5]通过声波检测手段对锦屏工程区的开挖损伤区进行了研究，将其分为爆破荷载和地应力高速释放引起的内损伤区，以及应力重分布引起的外损伤区；刘仲秋等[6]通过对内损伤区和外损伤区的围岩参数分别进行赋值，研究了流固耦合作用下开挖损伤区的分布情况；王军祥、袁小平和贾善坡等[7-9]建立了基于Druker-Prager(D-P)准则或者Mohr-Coulomb(M-C)准则的岩体弹塑性损伤模型，并利用模型对隧道开挖损伤区进行了计算研究.

1 岩石损伤渗流耦合模型

1.1 岩石弹塑性损伤模型

(1)

式中，ω为标量，表示岩石的损伤程度，取值范围为(0，1).在小变形理论的范畴内对应变ε进行分解，即

ε=εe+εp

(2)

式中：εe为弹性应变；εp为塑性应变.由各向同性的广义胡克定律可得有效应力的表达式为

(3)

式中，G为弹性刚度矩阵.

在有效应力空间对岩石塑性演化问题进行讨论，岩石塑性模型由屈服函数、流动法则、硬化律以及加卸载条件进行描述.本文采用Hoek-Brown屈服准则对岩石强度特征进行描述，即

(4)

(5)

(6)

(7)

式中：GSI为地质强度指标，取值范围为0～100；mi为表征岩石软硬程度的经验参数，取值范围为0.001～25.0；Q为考虑爆破对岩体影响的扰动参数，取值范围为0～1，0表示未受扰动的岩体.

岩体弹性模量表达式为

(8)

考虑流动法则时，为了解决棱线和尖点处无法求导的问题，将H-B准则看作多个应力状态与硬化参数K的标量函数组合，即

(9)

式中，K={mb，s}.硬化参数为塑性内变量κp的函数，即

K={κp}

(10)

(11)

(12)

式中：K0为硬化参数初始值；H为硬化模量.

软化参数与累积塑性应变的关系如图1所示.

图1 多线段软化函数Fig.1 Multiline softening function

假设塑性势函数与屈服函数具有相同的形式，即

(13)

式中，σcig、sg和mbg为塑性势函数对应的参数.

塑性应变增量dεp由对应的塑性势函数g1，g2，…，gn和塑性因子λ1，λ2，…，λn决定，其表达式为

(14)

Kuhn-Tucker加卸载条件为

dλifi=0 (dλi≥0，fi≤0)

(15)

1.2 损伤演化

相关研究多以幂函数的形式表征岩石损伤变量的演化规律，且考虑到损伤产生的阈值问题，本文选取损伤变量演化方程为

ω=1-exp(-α(κd-κd0))

(16)

式中：α为常数项；κd为损伤变量；κd0为损伤变量阈值.

选取等效塑性应变表征岩石损伤变量的演化，即

(17)

不同α值下，损伤变量ω与等效塑性应变的关系如图2所示.

图2 损伤变量演化规律Fig.2 Evolution law of damage variable

1.3 应力渗流耦合模型

由Darcy定律可得岩石稳态渗流场微分控制方程为

(18)

式中：p为孔隙水压力；kx、ky、kz分别为x、y、z轴方向的渗透率；Ss为单位贮存量；γ为水的重度.

(19)

式中：k0为岩石初始渗透率；n0为初始孔隙率；εv为体积应变.

渗流作用产生的孔隙水压p，通过多孔介质有效原理对应力场应力进行修正，其表达式为

σ′ij=σij-δijβp

(20)

式中：σ′ij为有效应力(压为正，拉为负)；β为等效孔隙压系数，0≤β≤1；δij为Kroneker符号.

2 耦合模型数值求解

2.1 塑性损伤模型本构积分算法

塑性演化与损伤分别发生在有效应力空间和损伤空间，彼此相互解耦，因此，可以利用文献[10]算子分离法对塑性变量和损伤变量分别求解，整个过程分为弹性预测、塑性修正和损伤修正三个部分.

1) 弹性预测.为了减少应力维数，使其在几何空间上的表达更为直观，本文选择在主应力空间对问题进行讨论.由给定应变增量求解弹性预测应力，即

σtrial=σA+GΔε

(21)

式中：σtrial为预测应力；σA为上一荷载步中的应力值；G为刚度矩阵；Δε为当前荷载步下的应变增量.

2) 塑性修正.塑性修正时，为了避免所求应力偏移屈服面，采用基于向后欧拉式的回映算法实现应力求解.利用边界面法对应力空间进行划分，如图3所示，根据预测应力的位置选择回映策略.当预测应力位于位置Ⅰ时，更新应力至尖点处；当预测应力位于位置Ⅱ时，更新应力至棱线l1上；当预测应力位于位置Ⅲ时，更新应力至屈服面f1；当预测应力位于位置Ⅳ时，更新应力至棱线l2上.

3) 损伤修正.应力更新完成后，将求得的塑性应变代入式(16)中更新损伤变量ω，即而由式(1)获得应力解.

图3 主应力空间中Hoek-Brown准则边界面划分域Fig.3 Divided areas of boundary surfaces with Hoek-Brown criterion in principal stress space

2.2 一致切线模量表达式

为了保证有限元方程组整体迭代求解过程中具有二阶收敛速度，给出一致切线模量的表达式为

(22)

式中：n为屈服面个数；Gc为修正后弹性矩阵，Gc=TG，T为修正矩阵；Δεp为塑性应变增量；A为n阶方阵.各变量的表达式为

(23)

(24)

式中，δij为Kronecker符号.ξi的表达式为

(25)

在主应力空间求得Gepc后，还应通过转置将其转化为六维空间下的直切线模量.

2.3 应力渗流耦合迭代过程

利用C++语言编制上述岩石弹塑性损伤模型求解程序，利用分布迭代法的思想，将其与课题组已有渗流求解程序seepage相结合，先计算岩石的应力场，然后根据渗透系数演化方程(19)计算单元渗透系数矩阵，继而进行渗流场计算，最后将求得的孔隙水压根据有效应力式(20)带回应力场求解程序中，反复迭代直至前后两次求得的应力场、渗流场满足收敛准则为止.耦合程序求解流程如图4所示.

3 工程应用

3.1 工程概况

吉林省甄峰岭隧道区入口段位于和龙市北部西镇区，出口段位于安图县松江镇境内.本文选取第四设计段K91+400 m断面进行开挖损伤区研究.该断面隧道底板埋深约为192.935～205.219 m，隧道围岩主要为玄武岩，块状构造，含少量气孔，节理裂隙发育，岩体呈碎裂块状结构，为棕褐色玄武岩，杏仁状构造.节理裂隙发育，碎裂结构，由BQ法求得围岩等级为Ⅳ级.隧道经过区属中温带湿润季风气候区，水量受季节变化较大，4～5月份积雪融化期、7～8月份雨季对地下水均有补给作用.开挖设计为台阶法施工，拱部采用光面爆破，边墙采用预裂爆破.

3.2 爆破开挖对围岩参数的影响

对爆破荷载作用下岩石初始损伤区进行研究，在距离K91+400 m断面20 m处布置辅助洞，设计4个间隔0.5 m的损伤区监测断面，每个断面布置两只相互平行的钻孔，用于声波对穿测试.图5为声波监测断面示意图，钻孔深度为25 m，孔径约为10 cm.声波波速值每50 cm采集一次，每次采样位置严格保持一致，测得不同监测面声波波速及声速降低率，如图6所示.

图4 耦合模型计算流程图Fig.4 Flow chart of calculation with coupling model

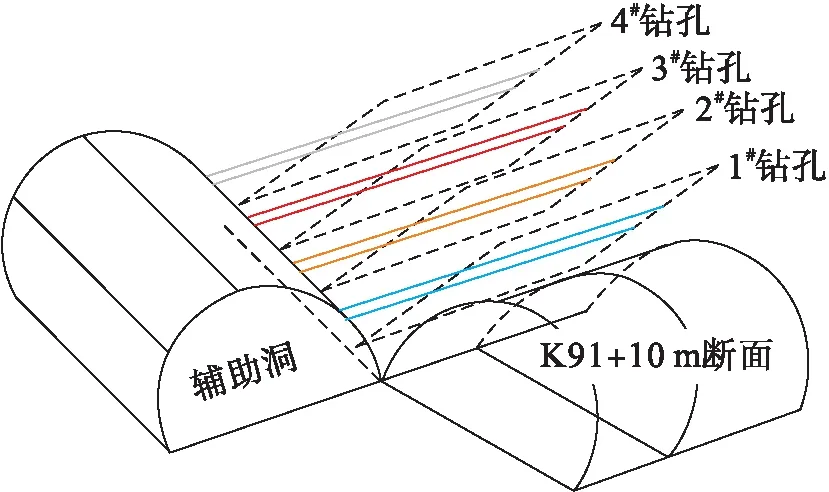
图5 声波监测断面示意图Fig.5 Schematic diagram of acoustically monitored section

由图6可知，爆破开挖前，4个监测断面处的声波监测值均在3 500～5 000 m/s之间.爆破后，4个监测断面的声波监测值发生不同程度下降，监测断面1处声波波速降低率在18.07%～33.01%之间；监测断面2处声波波速降低率在11.17%～17.64%之间；监测断面3处声波波速降低率在5.56%～10.99%之间；监测断面4处声波波速降低率在0.09%～5.06%之间.

岩体爆破损伤度Q与声速降低率η之间的关系为

Q=1-(1-η)2

(26)

由式(26)可以求得不同断面的岩体爆破损伤度，监测断面1处的岩体爆破损伤度为0.33～0.55；监测断面2处的岩体爆破损伤度为0.21～0.32；监测断面3处的岩体爆破损伤度为0.11～0.20；监测断面4处的岩体爆破损伤度为0.001～0.01.从最不利的角度考虑问题，确定岩体爆破损伤范围为1.5 m，爆破损伤度为0.55.

由现场设计资料估算围岩力学参数，围岩重度γ=25 kN/m3，GSI=35，μ=0.35，mi=16，a=0.52，由式(5)～(7)计算得爆破扰动区和未扰动区的Em、mb和s值(假设泊松比不随损伤发生变化，mb和s的残余强度为峰值强度的五分之一).根据文献[1]的研究，将爆破扰动区的初始孔隙度e0和水力渗透率k提高两个数量级，最终所得耦合模型计算参数如表1所示.

图6 爆破前后声波检测数据Fig.6 Acoustically monitored data before and after blasting

表1 计算参数Tab.1 Calculation parameters

3.3 计算结果分析

根据K91+400 m断面施工设计图纸建立有限元计算模型，如图7所示.模型高60 m，宽110 m，两侧施加水平位移约束条件，底部施加固定位移约束条件.模型顶部施加均匀的覆土荷载2.5 kN/m，左右两侧施加沿重力方向梯度变化的水头压力，底部水头高度Hd=56 m.整个模型共划分为1 084个节点和1 010个单元.

图7 有限元计算模型图Fig.7 Model for finite element calculation

计算时按照以下步骤对隧道开挖过程进行模拟：1)对模型进行数尺地应力平衡和渗流场计算；2)释放开挖荷载70%，进行初始爆破扰动区赋值；3)施加混凝土衬砌，释放剩余30%开挖荷载.

分别对考虑爆破效应和不考虑爆破效应的开挖损伤区进行数值模拟，所得结果如图8所示.由图8可知，考虑爆破效应的开挖损伤区范围要大于不考虑爆破效应，最终产生的最大损伤值为0.8，大于未考虑爆破效应时的最大损伤值0.65.洞周监测点计算位移值与现场实测位移对比如图9所示.考虑爆破效应时的位移远远大于不考虑爆破效应时的位移值，且更接近实测位移值.根据《城市轨道交通工程监测技术规范》，一级监测标准下隧道累积沉降预警值为20～30 mm，爆破作用下的计算值及监测值均已达到预警值，因此，应对该断面进行加固，避免工程灾害的发生.数值分析表明，爆破效应会加剧隧道最终的开挖损伤程度，这是在进行支护设计时必须考虑的问题.

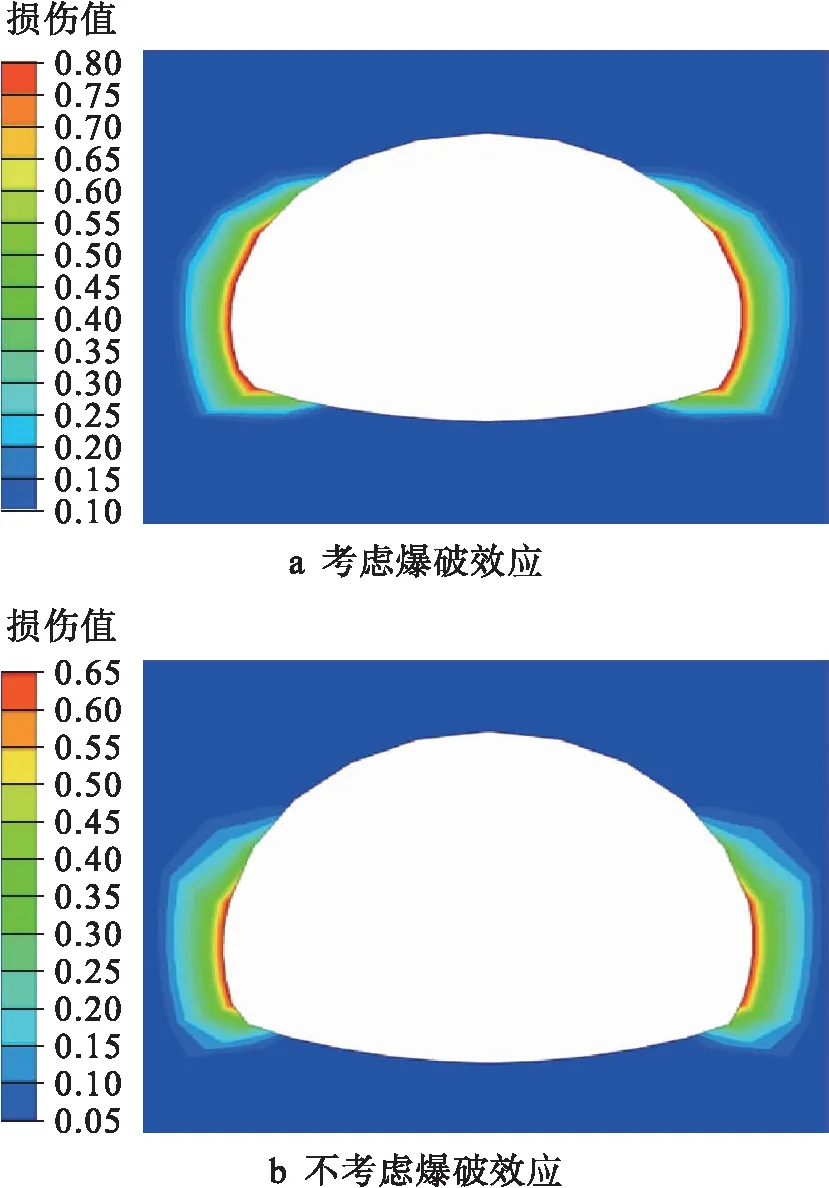
图8 开挖损伤区分布Fig.8 Distribution of excavation damage area

图9 位移对比Fig.9 Displacement comparison

对考虑爆破效应和不考虑爆破效应的渗流场进行计算，所得孔隙水压分布如图10所示.由图10可知，隧道开挖后对原有渗流场产生扰动，在隧道开挖区附近形成渗水漏斗.对隧洞周边单元流量进行求和，计算洞内涌水量(衬砌渗透系数为1.15×10-3m/d)，考虑爆破效应时的洞内涌水量为22 m-3·m-1·d-1，远远大于不考虑爆破效应时的10 m-3·m-1·d-1，与实测值20 m-3·m-1·d-1更为接近.

4 结 论

本文通过分析得出以下结论：

图10 孔隙水压分布图Fig.10 Distribution of pore water pressure

2) 利用声波监测手段确定研究断面处爆破作业产生的损伤区范围和损伤值大小，获得扰动系数Q的准确取值，对岩体力学参数mb、s和E进行修正.

3) 利用所建立耦合模型，对隧道开挖损伤区进行数值分析，结果表明，考虑爆破效应时的开挖损伤区及最大损伤值，洞周监测点的位移值及研究断面的洞内涌水量均有所增大，爆破效应对工程稳定性造成一定的威胁.