基于振荡波的干式空心电抗器绝缘检测系统*
2020-12-29王京保向天堂
陈 凌, 王京保, 刘 睿, 刘 策, 向天堂
(1. 国网四川省电力公司 a. 电力科学研究院, b. 广安供电局, 成都 610000; 2. 保定天威新域科技发展有限公司 技术中心, 河北 保定 071000; 3. 河北农业大学 机电工程学院, 河北 保定 071001)
近年来电网迅速发展,电抗器也在电网中大量应用.电抗器在调节电网无功功率方面发挥了重要的作用,并且在电网中电抗器也常用于滤波、限流等场合.干式空心电抗器具有独特的结构和优良的电气性能,其抗饱和能力强,能够耐受大电流的冲击,电抗值线性,质量轻,结构比较简单,故能在众多种类电抗器中脱颖而出[1-3].
与其他电器设备一样,由于各种原因,干式空心电抗器在投运后每年都会有多起恶性事故发生,导致空心电抗器烧毁,甚至爆炸,威胁电网的安全运行.其中造成其烧毁的主要原因是电抗器局部过热、散热不良及绝缘热老化等[4-6].若不能及时发现电抗器开始时便存在的微弱绝缘缺陷,绝缘问题会迅速扩大,造成更严重的事故,将会给电力系统带来巨大的经济损失和恶劣的社会影响.因此,及时准确地检测到电抗器初期的微小绝缘缺陷具有十分重要的意义.
针对干式空心电抗器在运行中常常发生的故障,干式空心电抗器保护与检测方法的研究显得尤为重要,但现阶段国内研究较少,而且主要集中在电抗器匝间绝缘试验上.文献[7-8]基于电抗器匝间短路对电抗器整体电感值的影响规律,研制了利用脉冲电压法测试电抗器绝缘故障的试验装置,能有效检测电抗器的绝缘缺陷.但在试验装置中球隙击穿后电弧不能马上熄灭,而导致球隙击穿瞬间变压器输出功率过大,使得变压器也参与到谐振电路当中,振荡频率不能真实反应电感的变化.感应电压、高频振荡能量吸收、直接施加工频电压等检测方法都能对绝缘缺陷进行有效检测[9],但是这些方法大多灵敏度不高,而且试验容量也相对较大.上述方法在研究上只是针对发生较大绝缘故障的电抗器而言,并不能很好地检测出电抗器潜在的绝缘隐患.
为了更及时、有效地检测到干式空心电抗器的绝缘故障,从而提高设备运行的可靠性,本文设计并实现了基于阻尼振荡波的干式空心电抗器绝缘检测系统.首先通过在MATLAB/Simulink上搭建仿真模型,确定充电电容的参数,以满足测试电抗器电压振荡波的频率、衰减情况等技术指标,使该系统的检测要求得到保证.之后研制试验装置并利用干式空心电抗器故障模型进行测试,通过试验数据对比得到绝缘缺陷严重程度不同的电抗器试验数据,验证了本系统不仅可以检测到发生绝缘故障的电抗器,还能检测到电抗器潜在的微小绝缘缺陷,达到了设计目的.
1 振荡波检测系统
本文设计的振荡波检测系统原理图如图1所示.图1中,试品干式空心电抗器由RX和LX组成,分压器由RZ1和RZ2组成,局放检测单元由Ck耦合电容和检测阻抗组成,振荡波系统由HVDC高压直流电源、Cd充电电容、R1保护电阻及SW高压电子开关组成.试验以干式空心电抗器为试品,电抗器的高压端连接充电电容末端,低压端接地.充电电容首端连接高压电子开关和保护电阻,保护电阻的另一端连接高压直流电源正极,高压直流电源负极接地.试验开始时,高压直流电源对充电电容进行充电,随着高压直流电源输出电压逐渐升高,充电电容两端的电压也随之升高;当充电电容两端电压达到额定电压时,高压直流电源停止工作,同时高压电子开关由分开状态切换到闭合状态;当高压电子开关闭合后,充电电容和电抗器组成阻尼振荡电路,系统主回路的充电电容和电抗器发生串联谐振,形成阻尼振荡波,同时在试品两端产生振荡电压.
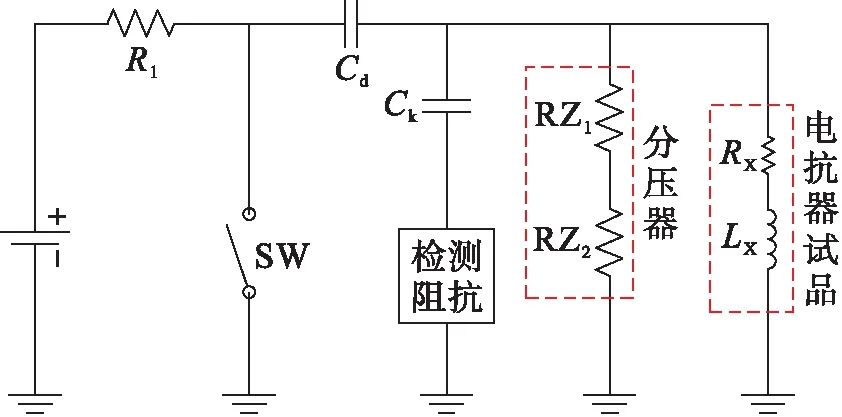
图1 振荡波检测系统原理图Fig.1 Principle diagram of oscillation wave detection system
由上述检测原理可以得知,干式空心电抗器中的RX、LX和充电电容Cd组成一个串联二阶谐振回路,串联二阶谐振回路工作过程可分为充电和放电两个阶段,充电过程相当于串联谐振回路的零状态响应.当充电电容充电完成时,充电电容达到额定电压,充电电容放电,系统处于放电过程,放电过程相当于串联谐振回路的零输入响应.检测系统主要监测电抗器两端电压,系统放电过程是本文研究的重点,因此主要分析放电过程.
在放电过程中,电感绕组上的过电压[10]为
(1)

(2)
转换到复频域为
LCs2+RCs+1=0
(3)
求解可得
(4)
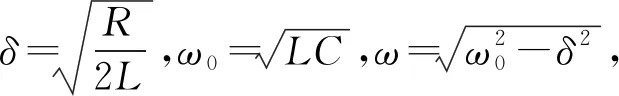
(5)
根据ω0和δ的大小,串联谐振回路分为4种情况,ω0>δ时,为欠阻尼;ω0<δ时,为过阻尼;ω0=δ时,为临界阻尼;ω0≪δ时,为无阻尼.在放电过程中需要确保电路为欠阻尼放电状态.
当δ足够小时,ω=ω0,此时电抗器上的电压可近似为
(6)
振荡波形仍为衰减振荡波,且包络线按指数衰减,此时电路的振荡频率为
(7)
根据式(7)得知,主回路参数的确定首先要获取干式空心电抗器的电感量范围,然后根据设计要求,例如振荡的频率范围、振荡电压的幅值来确定充电电容的电容量及功率,其干式空心电抗器的内阻和电感量决定振荡波检测系统的衰减系数.
2 主回路参数确定
在振荡波检测系统中,电抗器试品的电感量和内阻已经确定,主回路需要确定的参数为充电电容的参数,其使电抗器两端的电压振荡波满足该系统电抗器试验的技术指标.
2.1 基于不同频率的同种电抗器仿真
本文以不同规格型号的10 kV空心电抗器为试品,根据设计参数、振荡波仿真系统模拟不同型号的电抗器,根据其基本参数进行调节,进而对其他型号的电抗器振荡过程进行仿真.
本文参照的技术指标为:振荡频率为0.2~2 kHz;输出电压振荡持续时间在1 000 ms以内;输出电压波形的第一个和第二个振荡波峰值的衰减速度要满足设计要求;充电电容的充电时间小于3 s.
选择型号为CKGKL-33.4/10-5W的10 kV电抗器作为仿真和现场试验的主要依据,该型号电抗器的内部参数如表1所示.基于MATLAB/Simulink的系统主回路的仿真模型如图2所示.
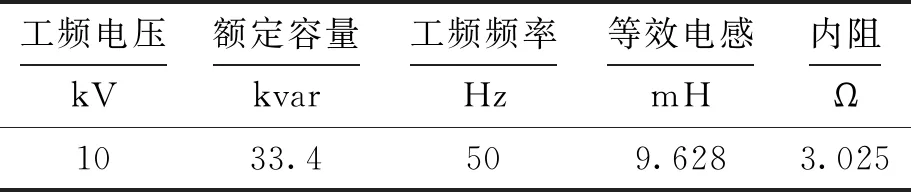
表1 干式空心电抗器参数Tab.1 Parameters of dry-type air-core reactor
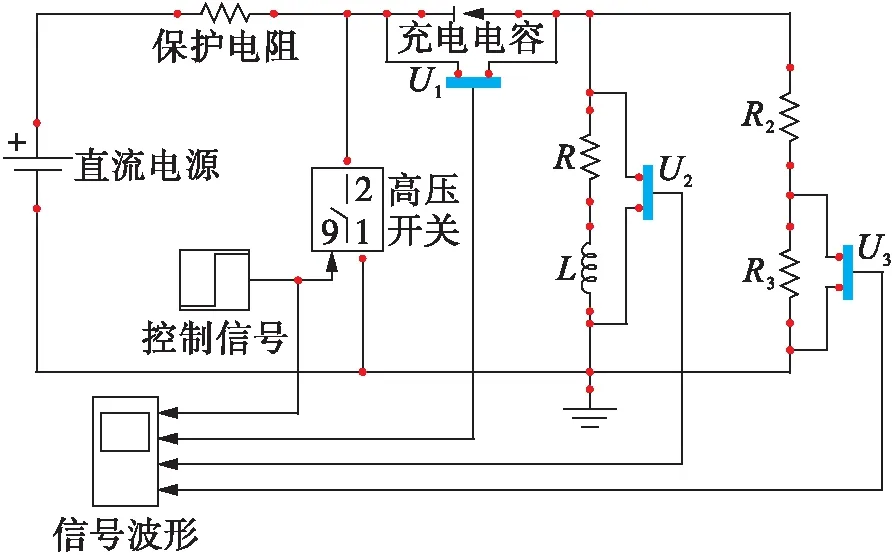
图2 主回路仿真模型Fig.2 Simulation model for main circuit
图2中,系统额定电压设置为30 kV,高压直流电源0~50 kV连续可调,保护电阻参数为10 kΩ,高压开关为阶跃信号控制的理想开关,几乎没有延时,其控制信号设置为0时表示高压开关为分开状态;设置为1时表示高压开关为闭合状态.电抗器等效成R和L,R参数为3.025 Ω,L为等效电感,参数为9.628 mH.R2和R3组成分压器,分压比为1 000∶1,R2为分压器高压臂,参数为50 MΩ,R3为分压器低压臂,参数为50 kΩ,系统中只有充电电容为待确定值.
设计三个不同的振荡频率参数,分别为0.5、1.0、1.5 kHz,由式(7)可计算出相应充电电容如表2所示.

表2 充电电容数值Tab.2 Charging capacitance values
根据设计参数要求,振荡波要保证一定的持续时间,不能衰减过快,至少要保证5个周期,如果振荡波持续时间短就不能正确地模拟电抗器在正常工况下的耐压状况.根据已知参数和式(6)可以计算电抗器两端上的振荡波电压为
(8)
试品的参数确定以后,将不同参数的充电电容输入仿真系统中,对振荡波主电路进行仿真,得到不同频率对应的电抗器电压波形如图3所示.
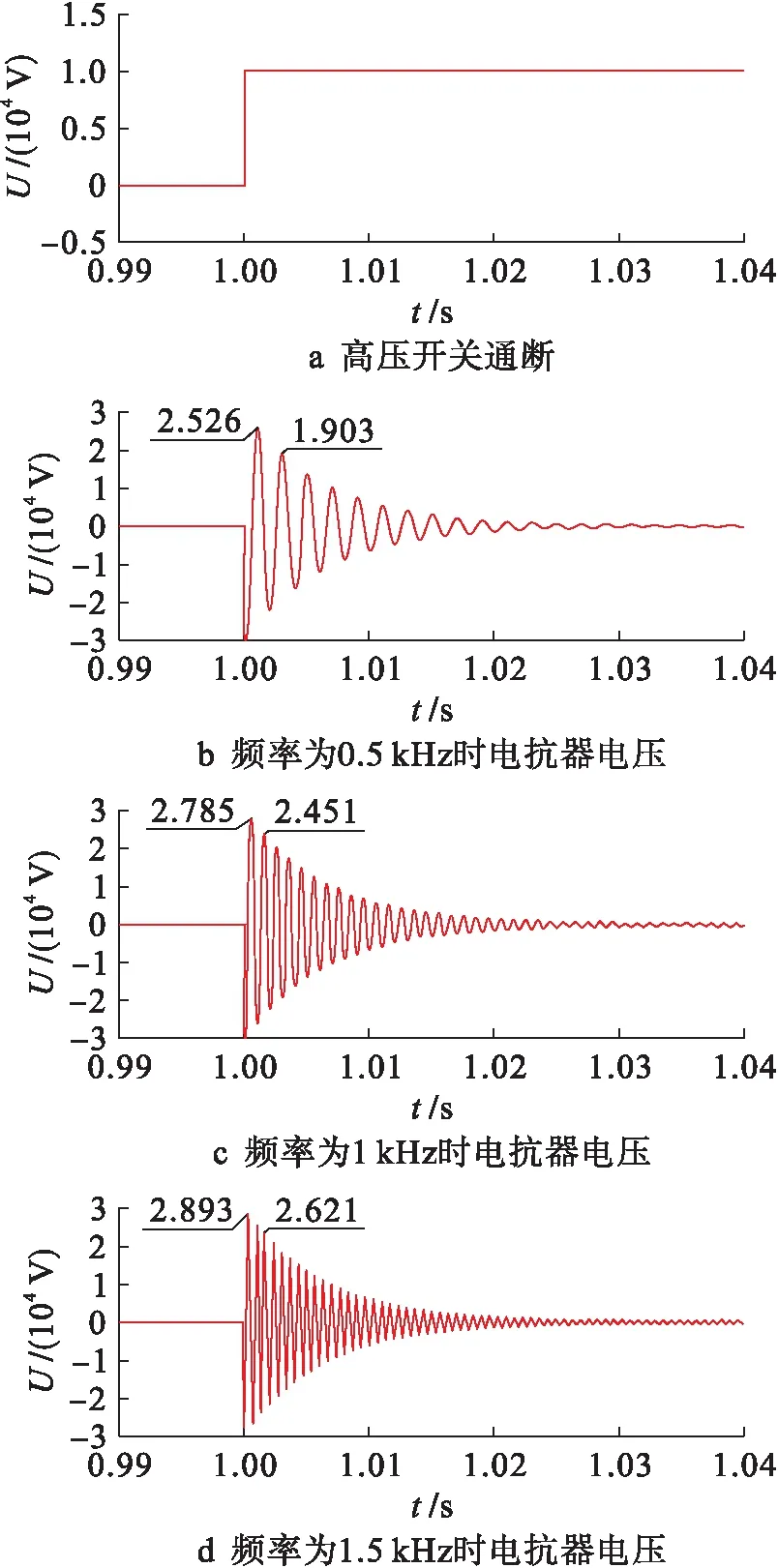
图3 电压波形Fig.3 Voltage waveform
由图3a可知,高压开关在0~1 s内为断开状态,保证充电电容的充分充电.1 s时开关闭合,充电电容和电抗器发生串联谐振,在电抗器两侧产生振荡波.由图3b可知,振荡波起始位置电压值为-30 kV,证明充电电容的充电时间小于1 s,振荡波在1 025 ms振荡完毕,振荡时间即电压保持时间为25 ms.振荡波经过12个周期衰减完毕,前两个波从25.26 kV衰减为19.03 kV,衰减速率为20.77%,电压衰减速率过快.由图3c可知,由于频率增大,振荡周期数增多.充电时间依然小于1 s,振荡波在1.027 5 s振荡完毕,即电压保持时间为27.5 ms,电压峰值从27.85 kV衰减为24.51 kV,衰减速率为11.13%,电压衰减速率有所减缓.由图3d可知,频率为1.5 kHz时,充电时间小于1 s,电压保持时间为30 ms,电压峰值从28.93 kV衰减为26.21 kV,衰减速率为9.07%,衰减的速率再次减小.
根据设计的技术指标,对仿真数据及其结果进行分析发现:3个不同参数的充电电容在干式空心电抗器参数确定的前提下,振荡频率有3种不同的结果,振荡电压持续时间基本相同.由于主电路的衰减系数由干式空心电抗器参数确定,系统振荡频率不同,输出电压衰减速率不同,振荡电压频率与输出电压衰减速率成反比.
2.2 主回路充电电容参数确定
根据现场实际需求,振荡波电压频率尽量接近试品实际工作的频率,但是这会增加充电电容的容量,增大充电电容的体积.考虑既能保证现场应用方便,又能达到良好的试验效果,将此次试验的振荡波频率确定在1 000 Hz左右;再结合表2中计算结果,将充电电容设计为固定值3 μF.
在图2的仿真模型中,分别选取规格编号为a、b、c、d的4种电抗器进行仿真,得到波形结果如表3所示.
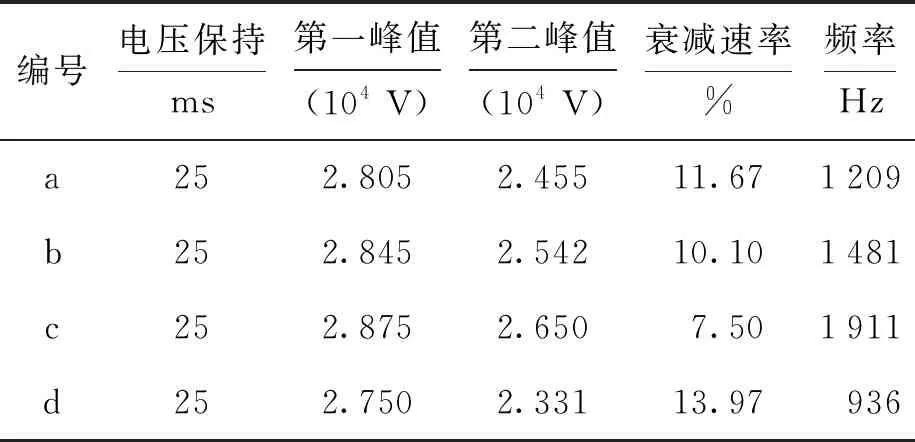
表3 振荡波形分析Tab.3 Analysis of oscillation waveform
由表3可知,a、b、c、d电抗器振荡波的频率在200~2 000 Hz之间,同样振荡波输出电压保持时间为25 ms,第一个峰值在27~29 kV之间,第二个峰值在23~27 kV之间,衰减百分比都在10%左右,衰减速率足够小,以上数据均达到了技术指标的要求.
截取参与试验的4种电抗器充电电容的充电情况,电压波形如图4所示.由图4可知,4种电抗器试验情况下的充电波形基本重叠,可见电抗器的不同对充电时间影响较小.波形中电容充电时间均为0.15 s,小于3 s,满足技术指标要求.
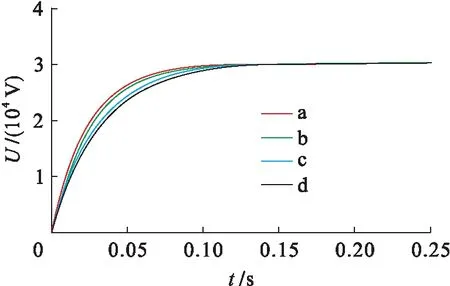
图4 充电电容充电过程Fig.4 Charging process of charging capacitor
综上可知,当主电路中充电电容设置为3 μF固定值时,对于各种电抗器产生的振荡波均能满足技术指标的要求.
本文设计的振荡波检测模型参数确定过程中,首先假定了几个特定的电路振荡频率,根据这几个频率确定其他参数,然后进行具体的仿真验证,这样能比较直观准确地说明问题,并验证该模型的可行性.而在实际测试过程中,无需要求振荡频率必须为某个确定的数值,只需要根据所测试的不同电抗器的具体电感值来设计多个具有不同电容值的电容器,即可保证主电路产生的振荡波的技术指标满足要求.
3 振荡波测试系统的现场应用
选取某变电站三个运行5年的10 kV串联干式空心电抗器进行试验,分别标注为1#电抗器、2#电抗器和3#电抗器.其中1#电抗器存在明显绝缘击穿的痕迹;2#电抗器外观与完好电抗器没有任何区别,但是经检查发现电抗器局部存在尖端毛刺;3#电抗器为完好电抗器,没有任何绝缘缺陷.分别将1#、2#、3#电抗器接入现场试验系统进行测试,测试现场如图5所示.

①高压直流电源 ②高压电子开关 ③试品电抗器 ④局部放电耦合电容器 ⑤局部放电综合检测仪 ⑥局部放电超声波传感器 ⑦局部放电特高频传感器 ⑧局部放电高频传感器
试验在振荡电压初始值为30 kV时所得的电抗器振荡电压的波形如图6所示.纵向比较系统振荡电压波形数据可以明显看出:电抗器存在明显匝间绝缘故障时,1#电抗器两端的振荡电压波形的衰减率要高于完好的3#电抗器,同时振荡波形的周期缩短,振荡频率增加.但是,对比2#电抗器、3#电抗器波形数据,发现振荡波并无明显变化.
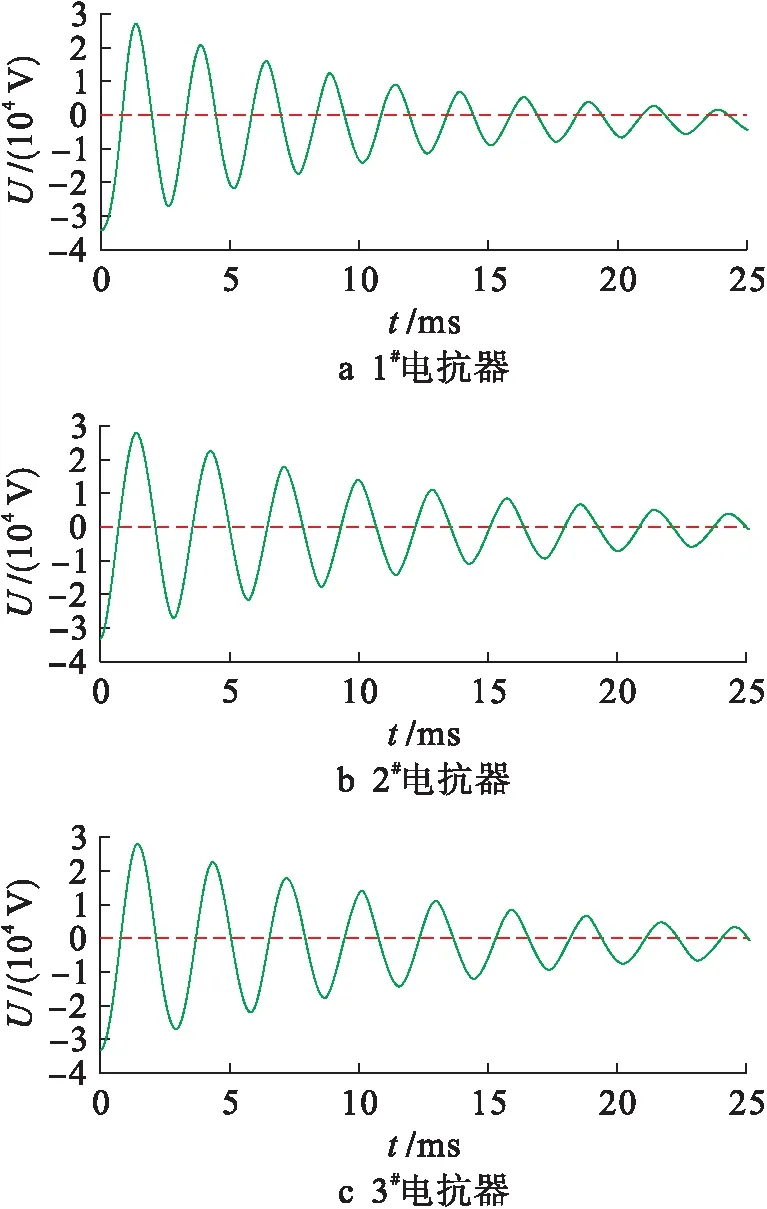
图6 试验电抗器电压波形Fig.6 Voltage waveform of test reactor
进一步对各电抗器的电压波形进行分析,取5~30 kV不同的振荡电压等级对三个电抗器进行试验,得到不同电抗器两侧的振荡波频率变化如表4所示.
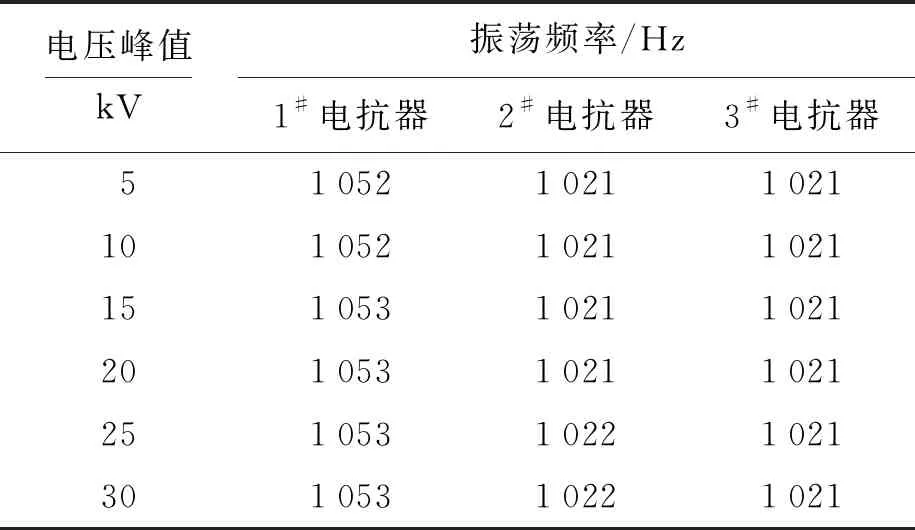
表4 试验电压波形分析Tab.4 Analysis of test voltage waveform
由表4数据可知,以完好3#电抗器的振荡频率为基准,存在明显缺陷1#电抗器的振荡频率明显增大,而存在尖端毛刺的2#电抗器频率的变化并不明显.为解决此问题,引入局部放电检测策略对电抗器局部放电进行检测,得到检测结果如表5所示.
通过表5数据对比可以清晰看到,当电抗器存在微小的尖端毛刺时,局部放电检测数值明显增大,能直观清晰地判断2#电抗器存在微小绝缘缺陷.
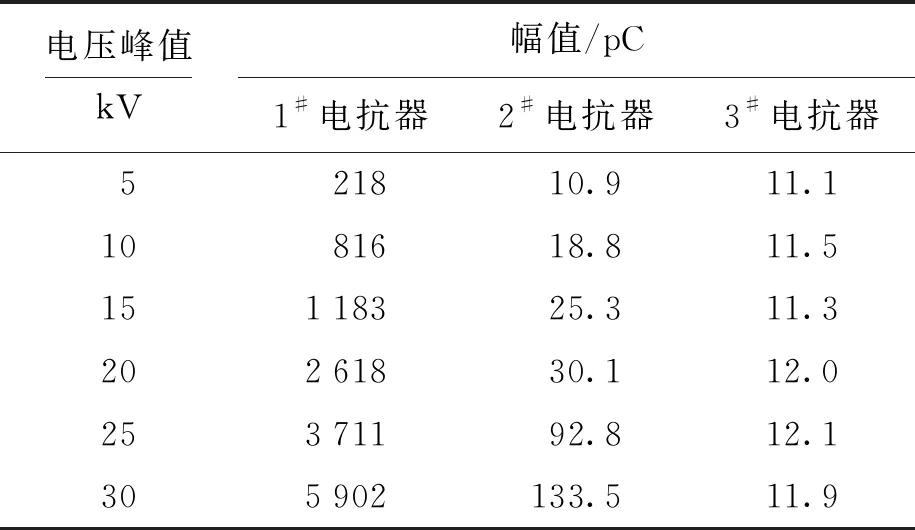
表5 局部放电数值分析Tab.5 Numerical analysis of partial discharge
4 结 论
针对电抗器存在的不同程度的匝间绝缘缺陷现象,本文设计基于阻尼振荡波的干式空心电抗器绝缘检测系统.在MATLAB/Simulink中搭建模型并进行仿真,确定充电电容的参数后在现场进行了试验验证,得到了如下结论:
1) 主电路中待确定充电电容值设置为3μF时,对任意规格的电抗器进行测试,所产生的振荡波都能达到技术指标的要求.
2) 电抗器存在匝间绝缘故障进行试验时,由于电感量的变化,短路匝内的环流增加了电抗器的损耗,故加快了振荡电压衰减速度,同时振荡波的振荡周期减小,振荡频率增大.
3) 本文所设计的振荡波测试系统引入局部放电的检测手段能清晰直观地检测到干式空心电抗器潜在的绝缘缺陷,从而能有效避免绝缘故障的进一步扩大,防患于未然.
