数学教学的另一种方法

白书宁

【摘要】

几十年来，数学教育教学在很大程度上依赖于教师向学生展示正确操作的范例练习，作为他们自己练习时的榜样.近年来，为了给学生进行错误分析，引入了不正确的练习.将正确工作的练习与错误分析相结合，这给研究人员提出了更高的数学理解.方法：一种混合方法被用来调查在七年级数学单元中对方程和不等式的错误分析.定量数据用于建立使用错误分析有效性的统计，定性方法用于理解参与者的错误分析经验.结果：测试后得分没有显著差异，然而，延迟后测试成绩有显著差异.结论：总的来说，老师和学生发现使用错误分析在学习过程中是有益的.

【关键词】错误分析;正确和错误的例子;数学教学实践;数学实践标准

一、引言

几十年来，数学教育的教学方法基本都是教师在课堂上向学生展示正确的解题步骤，随后让学生依据教师演示的步骤进行自我训练并解答书本或是练习册上的习题.在数学考试之后也是遵循这样的流程，教师向学生展示解题的正确步骤，然后让学生依据正确的答案进行对照和自我修改.这样的教学方法貌似已经成为数学教学的金科玉律，在以往的教学过程中也没有遭到什么质疑与抨击.但随着社会的快速发展，越来越需要灵活与创新型的人才，而不是一味地遵循硬性规定的员工.数学作为锻炼逻辑与解决问题能力的基础学科，教师教授它的目的不是让学生学会如何考试、如何计算，而是培养学生解决问题的逻辑和思维模式.在这种情况之下，传统的正确演示式教学就不甚合适，它虽然可以帮助学生取得较好的学业成绩，但对于创新性的培养有所欠缺.

由此，错误分析法应运而生.错误分析法指的是针对学生做错的题目进行分析，包括犯错误的原因以及后果，以往的研究认为分析学生做错的题目是另一种强化的形式，会导致学生对错误的方法更加印象深刻，进而促进个体下次继续犯同样的错误.但是，最近的研究表明，错误分析法并不是强化学生的错误做法，而是帮助学生深刻认识到自己出现错误的原因，其强化的是学生对自己犯错误过程中的错误的思维模式，能够在根本上探析学生的内部认知模式.并且，错误分析法可以帮助学生构建全面完整的认知图式，而不是集中于正确的问题解决方式.错误分析法不仅可以从根本上杜绝学生错误的思维模式，还能够完善学生的认知图式.最终促进学生更好地将该模式迁移到更广阔的领域之中，更好地迎合社会的需求.然而，目前在数学教学中关于错误分析法的研究十分匮乏，因此，本研究拟检验错误分析法在数学教学中的有效性.

二、研究目的

本研究的目的是探索七年级学生是否可以从正确范例和错误分析的使用中将数学学习得更好，而不是从更传统的解决练习的教学方法中学习，在这种方法中，学生只接受正确范例的指导.这项研究通過调查教师和学生在错误分析方面的经验反馈，进一步推进了以前关于从正确的例子和错误分析中学习这一主题.本研究回答了以下问题：

1.当错误分析被包括在学生的课程和作业中时，与传统的仅通过正确例子学习的方法相比，数学成绩有什么不同？

2.当错误分析包含在学生的课程和作业中时，相对于仅通过正确例子学习的传统方法，学生和老师观察到了什么样的好处或缺点？

三、研究方法

一种混合方法设计被用来调查在七年级数学单元中对方程和不等式的错误分析的使用.使用定量数据来建立使用错误分析有效性的统计，使用定性方法来理解参与者在错误分析方面的经验.

（一）研究对象

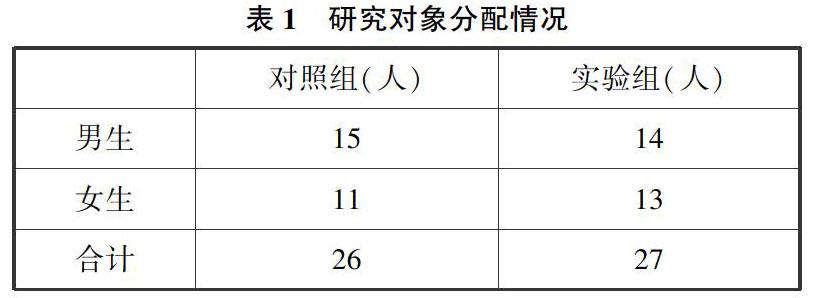
黑龙江省大庆市两所学校的七年级数学班使用一个方便的分组组成了对照组和实验组.26名学生为对照组，27名学生为实验组.同一个老师教两组学生，所以可以从老师的角度对学生如何学习和参与在两组间进行比较.在学习开始时，老师愿意在她的教室里尝试错误分析，然而，她并不热衷于使用这种策略，她无法想象错误分析如何在日常工作中发挥作用.到研究结束时，老师变得非常热衷于在七年级数学课上使用错误分析.其中，29名男生，24名女生（如表1）.

（二）研究材料

创建了一个前测和后测，其中包含的问题将使用格伦科数学：你的共同核心版CCSS作为资源来测试对方程和不等式的数学理解.从格伦科数学：你的共同核心版CCSS教科书中为对照组和实验组都创建了家庭作业，然而，研究人员重写了两到三个作业练习作为错误的例子，让实验组找出错误，并用正当理由修正练习.研究人员对两组学生都使用作业时间日志来跟踪他们花在家庭作业上的时间.

三、研究结果

进行初步分析以评估t检验的假设.这些假设包括：（a）独立性，（b）用夏皮罗-维尔克检验进行正态性检验，（c）用莱文统计量进行方差齐性检验.所有假设都得到满足.

前测成绩的Levene统计（p>0.05）表明各组间无显著性差异.进行独立样本测试，以确定错误分析对学生成绩的影响，错误分析是由前测和后测以及前测和后测延迟手段的差异决定的.对照组（M=8.23，标准差=5.67）和实验组（M=9.56，标准差=5.24）的后测得分无显著差异;t（51）=0.88，p=0.381（如表2）.然而，对照组（M=5.96，标准差=4.90）和实验组（M=9.41，标准差=4.77）的延迟后测得分有显著差异;t（51）=2.60，p=0.012（如表3）.这些结果表明，学生可以通过各种方法初步学习数学概念.然而，当错误分析被添加到学生的课程、作业和测验中时，数学知识的保留会显著增加.值得注意的是，实验组（M=9.56）与对照组（M=8.23）从前测到后测的平均值之间的差异更大，这意味着即使平均值没有显著差异，实验组确实显示出更大改善.

由于通过让每组中的一小部分人参与跟踪完成家庭作业所花费的时间，因此测试分析的结果不能用于任何概括.然而，分析的结果很有趣.使用独立的样本t检验来计算和分析每组完成作业所花费的平均时间.对照组（男性=168.30，标准差=77.41）和实验组（男性=165.80，标准差=26.53）学生花在家庭作业上的时间没有显著差异;t（13）=0.07，p=0.946（如表4）.这些结果表明，学生花在家庭作业上的时间几乎是一样的，不管他们是必须进行错误分析（找出错误，纠正错误，并证明所采取的步骤是正确的），还是以传统的方式按照正确的例子解决每个练习.尽管学生课外做作业的时间没有明显不同，但实验组在课堂上确实花了更多的时间进行测验修正和讨论错误，这些错误可以归因于知识的保留.

四、讨论

研究结果表明，教师采用正确演示法与错误分析法对学生进行教学的即时效果没有显著差异，这说明学生在接触数学的新知识的时候，教师采用正确演示法与错误分析法都可以很好地被学生接受，这可能是因为学生在构建新的知识图式时只是在进行知识纳入而不进行更为深层次的加工，不管是什么样的知识输入方式，都会经过相同的知识输入路径，因此，在教授新的数学概念和知识时，教师可以依据自己的教学习惯任意选择传统的正确演示法或错误分析法.进一步的研究结果还表明，在旧知识的巩固上，错误分析法比正确教学法的效果更佳.这说明错误分析法能够将旧知识进行更好的提取，并且进行更深层次的记忆.这提示教师在复习旧知识的时候应该尽量采用错误分析法.

五、结论

通过实证研究本研究得出以下结论：

（1）教授新知识的过程中，数学教师采用正确演示法与错误分析法的教学效果没有显著差异.

（2）巩固旧知识的过程中，数学教师采用错误分析法的教学效果更佳.

（3）错误分析法对教师的教和学生的学都很有益处.

【参考文献】

[1]Using erroneous examples to improve mathematics learning with a web-based tutoring system[J].Computers in Human Behavior， 2014， 36：401-411.

[2]Glencoe M G， McGrawHill/Glencoe.Algebra 2 Student Edition CCSS[J].Business & Economics， 2012.

[3]Mclaren B M， Adams D M， Mayer R E.Delayed Learning Effects with Erroneous Examples： a Study of Learning Decimals with a Web-Based Tutor[J].International Journal of Artificial Intelligence in Education， 2015， 25（4）：520-542.

[4]Tan Sisman G， Aksu M.A Study on Sixth Grade Students Misconceptions and Errors in Spatial Measurement： Length， Area， and Volume[J].International Journal of Science and Mathematics Education， 2016， 14（7）：1293-1319.

[5]Tsovaltzi D， Melis E， Mclaren B M， et al.Learning from erroneous examples： when and how do students benefit from them[M].Sustaining TEL： From Innovation to Learning and Practice，2010.

[6]Corder， S.P.The Significance of Learners Errors.[J].International Review of Applied Linguistics， 1967， （4）： 161 - 170.

[7]Jiabin Liu，Qinghe Fang，Anxin Guo，Hui Li.Error analysis of reconstructed wave force on a circular cylinder by using wave elevation data[J].Ocean Engineering，2020，209.

[8]陳俊杰.小学生分数除法错误研究[D].济南：山东师范大学，2018.

[9]蔺云.高等数学习题错误分析及教学对策[J].高师理科学刊，2015（07）：73-78.

[10]杜广华.对比分析法、错误分析法和语际语理论间的关系（英文）[J].山西农业大学学报，1997（04）：77-79+95.

[11]李善良.数学概念学习中的错误分析[J].数学教育学报， 2002（03）：6-11.

[12]王槐晟，兰德新，詹佩玲.谈数学教学中的错误分析、预防与利用[J].数学之友，2019（08）：6-10.

[13]高宇.初中生数学解题错误纠正策略效果研究[D].长沙：湖南师范大学，2017.

[14]李琛.初中生数学运算错误诊断分析：以苏科版教材七年级下教学内容为例[J].中学数学月刊，2016（12）：36-38.

[15]王鹏飞.数学教学中学生“错误观”的调查与分析[J].西部素质教育，2016（03）：7-9.

[16]杨丽蓉.初中生有理数学习中的错误分析及教学对策研究[D].上海：上海师范大学，2015.