P91钢多层多道同质补焊残余应力的数值模拟

郭庆虎， 胥国祥， 陈东高， 马良超， 王大峰， 唐家耘

(1.中国兵器科学研究院宁波分院，浙江 宁波 315000；2.江苏科技大学，江苏 镇江 212000；3.宁波表面工程研究院有限公司，浙江 宁波 315000)

0 前言

P91钢是一种改良的马氏体耐热钢，它在9Cr-1Mo钢的基础上降低了C 元素含量,进一步控制S，P 元素的含量，并添加少量 V，Nb 和 N 等元素进行合金化而获得的钢种。因其优良的高温性能被广泛应用于电力行业。P91钢在服役过程中不可避免地会在管道的表面和内部产生一些裂纹，从而使得焊接结构的返修率增加，大大降低了生产效率。补焊工艺因具有修复效率高、经济成本低、便于操作等特点，在火电行业多采用补焊的方式对管道局部缺陷进行修复。由补焊过程中引起的焊接残余应力会在一定程度上恶化补焊区域的综合性能。此外，相较于低合金钢，P91钢的马氏体相变温度较低(100～400 ℃)，马氏体相变会对P91钢补焊接头残余应力分布产生显著的影响。然而，马氏体相变对多层多道焊接头残余应力的影响十分复杂。研究表明：马氏体相变不仅可以改变焊缝及HAZ残余应力数值的大小，甚至可能改变应力的符号，由拉应力转化为压应力[1]。对于多层多道焊接接头来说，采用试验的方法并不能完全反映补焊结构表面和接头内部的应力分布状态。分析多层多道补焊区域残余应力的三维分布特征对澄清马氏体相变在应力形成中的作用具有重要意义[2-4]。随着计算机技术在焊接领域的拓展，有限元数值模拟已经成为了预测焊接残余应力的有效工具。然而，到目前为止，关于固态相变对P91钢多层多道补焊残余应力的影响还鲜有研究[5-8]，如果能澄清以上问题，将为优化补焊工艺提供理论基础。

基于热弹塑性力学理论，建立了固态相变的“热-冶金-力学”耦合的三维有限元模型，数值模拟了P91钢多层多道补焊试件的温度场和残余应力，分析了固态相变对P91钢多层多道补焊残余应力的影响。该研究对于揭示固态相变对P91钢多层多道补焊残余应力影响机理具有重要的理论意义，同时对于优化补焊工艺以及调控多层多道焊接接头残余应力的分布状态具有重要的工程应用价值。

1 试验方法

采用ZX7-315逆变直流电弧焊机进行P91钢补焊试验，其中母材为P91钢，其化学成分见表1。焊接材料为P91钢焊条。图1所示为补焊试样。焊接之前确定缺陷的类别及缺陷区域的大小，采用机械加工的方法清理缺陷，开U形槽，槽深与开口表面横向宽度大小比例为 15∶14，坡口底部要留有足够的宽度以利于后续补焊工艺顺利实施，两端的凹槽结合要平稳过渡避免在过渡处产生应力集中，补焊坡口内部不得有台阶或死角、氧化皮、铁锈、油污等。开U形坡口，坡口深度30 mm、宽度28 mm。根据P91钢补焊的工艺参数和坡口的几何特点，试验采用多层多道补焊的方式，补焊试验的焊接工艺参数见表2。共计填充34道焊缝，其中补焊试件的三维尺寸及焊道布置如图2所示。

待补焊试样焊接完成后，对焊件表面进行机械打磨，去除焊件表面铁锈、油污等杂质，直至焊件表面露出金属光泽。采用丙酮清洗待测区域表面，粘贴应变片(BE120-2CA-K)，待胶水完全凝固后，连接应变检测仪(BZ2205C)。安装盲孔发钻孔设备，钻头直径1.5 mm、钻孔深度2 mm，待示数稳定后读取结果。

表1 P91钢化学成分(质量分数，%)

图1 补焊试样

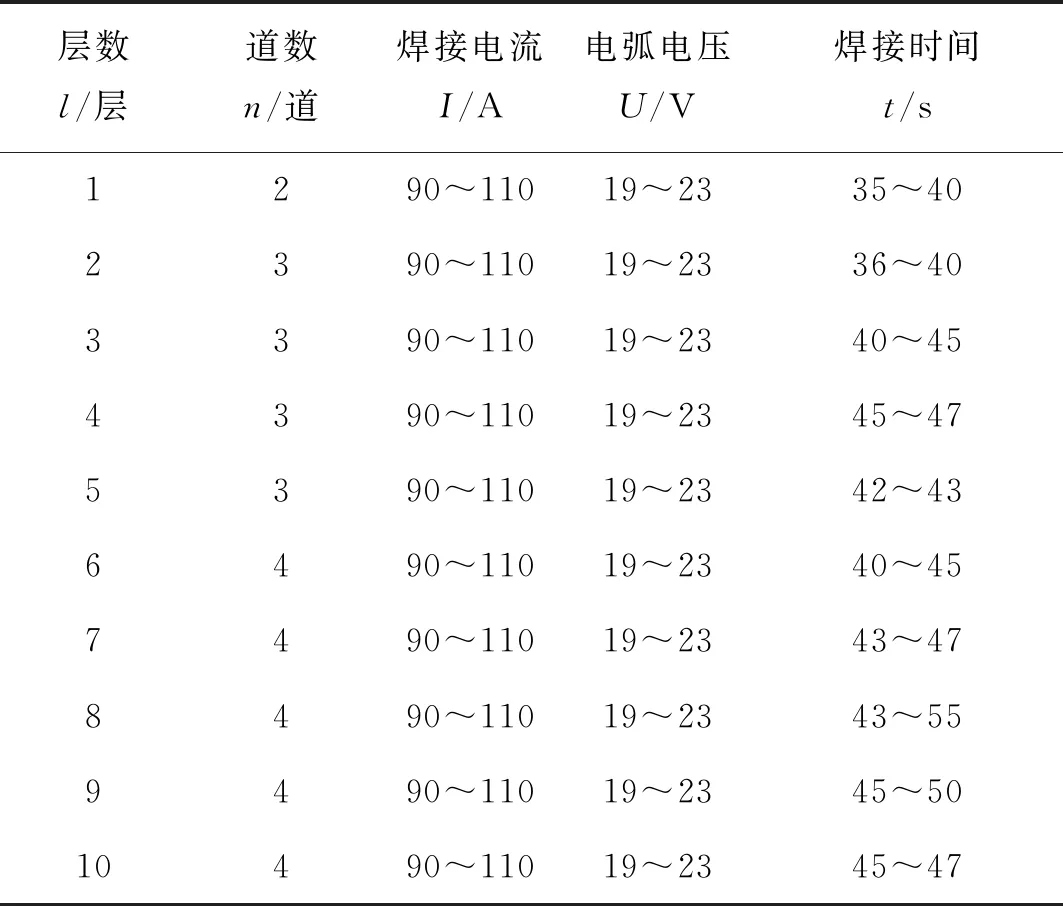
表2 补焊试验的焊接工艺参数

图2 试件三维尺寸和焊道布置示意图

2 有限元模型

建立考虑固态相变的热-冶金-力学三者耦合的三维有限元模型。数值模拟了P91钢多层多道补焊试件的温度场和残余应力，旨在描述采用同质填充材料(P91钢焊条)条件下，补焊结构的应力分布特征及固态相变对残余应力的影响。在数值模型中，采用双椭球热源模型来描述焊条电弧焊的热输入，考虑材料在高温下的热物性参数和边界条件来计算焊接温度场和残余应力。同时，还计算了焊缝及热影响区在加热和冷却过程中各个节点的组织成分变化过程。

2.1 温度场数值分析

在焊接温度场数值的计算中，仅考虑固体热传导过程中，而忽略熔池内部流体流动对传热的影响。采用非线性热传导方程来描述焊条电弧焊产生的热量在焊件内部的传导。瞬态热传导控制方程如式(1)所示[9-10]。

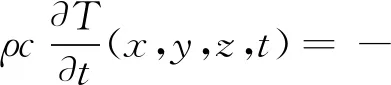
(1)

式中：ρ为材料密度；c为比热容；T为室温温度；q为热通量矢量；为拉普拉斯算子;Q为内部热量生成率。

在计算温度场时考虑焊件表面对流换热qc、辐射qr，其控制方程表达式如式(2)所示。

(2)

式中：qloss为总热量损失；hc为对流换热系数，在计算中假定其不随温度变化并取值30 W/(m2·℃)；ε为热辐射系数；σ为史蒂芬-玻尔兹曼常数，设其值为5.67×10-8W/(m2·℃4)；T0为室温温度。

对于焊条电弧焊，热量主要来自电弧的热输入，电弧具有体积热源特征，采用双椭球热源模型来描述焊条电弧焊的热流密度分布，其热流密度分布函数如式(3)、式(4)所示。

前半球热流密度分布函数：

(3)

后半球热流密度分布函数：

(4)

式中：ff+fr=2；a1,a2,b和c是双椭球热源参数。

同时，计算前，根据补焊试样的实际尺寸和坡口形状特点，建立补焊试件的实体模型。综合考虑计算精度和计算效率，对其进行非均匀化网格划分，焊缝及近缝区网格尺寸较小，而远离焊缝区域则网格的尺寸较大，如图 3 所示。计算中采用“生死”单元法描述焊缝金属填充过程。

图3 有限元模型

2.2 组织成分演变数值分析

受焊接热循环影响，P91钢焊缝及近缝区在加热过程中发生奥氏体化过程，同时在冷却过程中发生了高温奥氏体向马氏体转化的过程。在数值模拟中，奥氏体化过程采用Johnson-Mehl-Avrami关系描述[10-11]：

(5)

式中：P是在相平衡时获得的比例；TR是与反应相关的延迟时间；n是表征相增长率的指数，假定其与温度有关。

在计算中，热场和组成成分比例的计算同时进行。由于P91钢的成分特点，在大热输入与预热条件下，在冷却过程中也只发生高温奥氏体向马氏体的转化。在冷却过程中马氏体相变采用Koisten-Marburger关系描述[12]：

(6)

式中：fM是马氏体的比例；P是在是未回火马氏体在室温下的百分比，通常假设为1；b是转变速率，这是一个常数，假设为0.011；MS表示P91钢的马氏体转变起始温度为375 ℃。

2.3 焊接应力场数值分析

为了简化计算及提高计算的收敛性，采用间接耦合法计算焊接残余应力，即将温度场计算获得的热载荷加载到应力-应变计算模型中进行求解。计算时仅考虑温度场对组织成分演变和应力应变的影响，而不考虑后两者对温度场的影响。同时，将获得的组织体积百分比的计算结果也代入到应力-应变计算模型进行求解。在计算过程中考虑材料热物理性能随温度变化的特征，P91钢的热物理性能和力学性能参数如图4所示，其中P91钢焊条的热物理性能与P91钢热物理性能相似，与温度有关的力学性能、应力应变在微小的时间增量内线性变化。在应力分析模型中只施加了防止刚体发生平动和转动的边界条件。应力场分析用到的有限元模型和温度场分析中用到的模型相同。任意一点材料总的应变包括热应力引起的弹塑性应变，相变过程引起的体积应变、相变塑性应变和蠕变应变。焊接过程中，蠕变应变通常可以忽略不计[13]。总应变增量可以表示为：

Δε= ΔεE+ ΔεP+ΔεT+ΔεV+ΔεTr

(7)

式中：ΔεE, ΔεP，ΔεT，ΔεV和ΔεTr分别为弹性应变增量、塑性应变增量、热应变增量、体积应变增量及相变塑性应变增量。

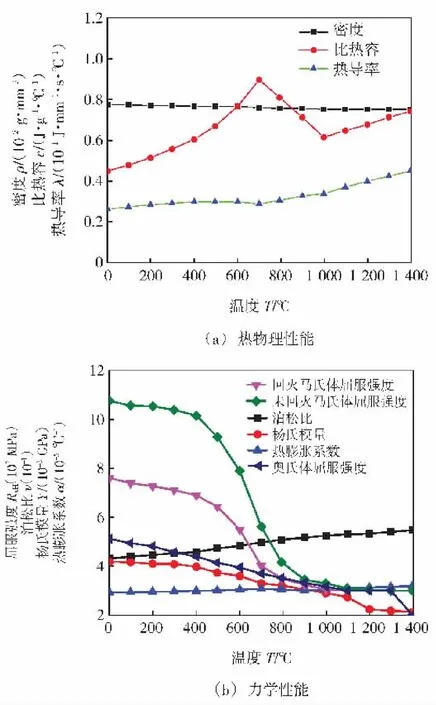
图4 P91钢材料的热物理性能和力学性能

奥氏体完全转变为未回火马氏体后其应变增量约为0.007 5[14]，对于冷却过程中马氏体相变，由马氏体相变引起的体积应变增量为：

ΔεV=0.007 5gfm

(8)

在该研究中，Leblond模型用来考虑由固态相变引起的相变塑性。相变塑性模型的表达如下：

(9)

计算过程中，热应变通过线膨胀系数表征，弹性应变遵循胡克定律，塑性区内材料的行为遵循塑性流动准则和各向同性强化准则[15]。

3 结果与讨论

3.1 温度场结果

图5给出了计算所得熔合区尺寸和图5a中A点热循环曲线，图中黑色实线为补焊坡口的边界。P91钢熔点约为1 450 ℃，从图5a中可以看出熔点以上区域的范围超过了补焊坡口的边界。另外，从A点热循环可以看出，预热温度为100 ℃，层间温度介于150～200 ℃之间，最高加热温度约为2 300 ℃，与实际焊接过程符合，证明了温度场计算结果的合理性。图6给出了图5中A点的组织成分演变曲线。可以看出，在焊接加热过程中，A点微观组织逐渐由回火马氏体转为马氏体，奥氏体的比例随焊接时间的增加而减小。待补焊试件冷却至室温，初始相完全转化为未回火的马氏体，回火马氏体和奥氏体完全消失。

3.2 应力场结果

图7给出了考虑和不考虑固态相变条件下补焊试件残余应力三维分布云图。从图中可以看出固态相变效应对补焊试件残余应力分布特征的影响较为明显。从图7a和7b可知，固态相变能够使得末道焊缝及其附近热影响区表现为较为明显的横向压应力。产生这种现象的主要原因是固态相变引起的体积膨胀松弛了因热收缩产生的拉应力；不考虑固态相变时，熔合区上表面表现为明显的横向拉应力。对于纵向应力来说，考虑固态相变条件下，试件上表面纵向应力呈现出拉应力、压应力交错分布的特征。当忽略固态相变效应时，试件上表面表现为拉应力，其中末道焊缝及其附近热影响区产生了明显的拉应力集中，这主要是由于末道焊缝的填充金属在冷却过程中的收缩受到周围金属的抑制，因而产生了较大的拉应力。另外，受补焊坡口结构形式影响，起弧端和熄弧端处母材会对焊缝填充的膨胀和收缩产生明显的抑制作用。从图中可知，考虑固态相变条件下，横向残余应力在起弧端和熄弧端处为拉应力，末道焊缝两端为压应力。纵向残余应力在起弧端应力数值较小，局部为压应力，熄弧端出现了较小的拉应力；不考虑固态相变时，横向应力和纵向应力在起弧端和熄弧端均为较大的拉应力。分析产生以上现象的原因是固态相变引起的体积膨胀、力学性能变化能够使得局部的拉应力转化为压应力。不考虑固态相变时，起弧端和熄弧端区域并不会产生残余应力松弛的现象，因而表现为较大的拉应力。坡口形式对金属收缩的抑制也会使得拉应力的集中更为明显。

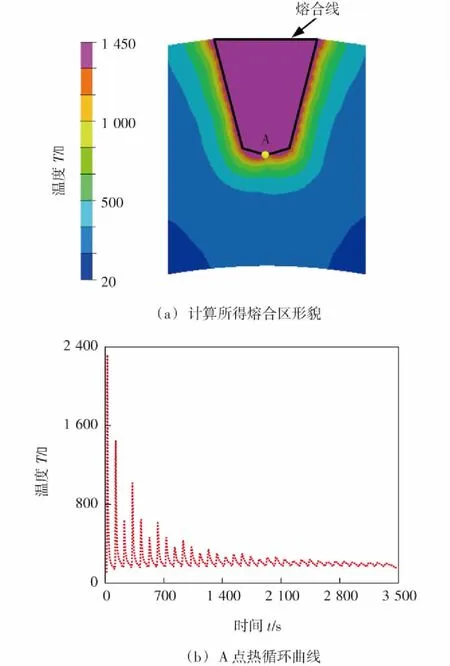
图5 温度场计算结果

图6 组织成分随试件变化曲线

图7 P91钢补焊残余应力三维分布云图

图8给出了补焊试件中心横断面应力分布云图。从图中可以看出，考虑固态相变时，横向应力熔合区的中上部产生了明显的应力集中，在末道焊缝处表现为明显的压应力。不考虑固态相变时，横向应力在近表面产生了明显的拉应力集中。在沿壁厚方向上，随着上表面位置距离的增加，横向应力在逐渐减小。对于纵向应力，固态相变效应对熔合区中下部区域的应力分布特征影响不大。考虑固态相变时，纵向应力在近表面呈现出拉应力、压应力交错分布的特征。不考虑固态相变时，熔合区表现为较大的拉应力，末道焊缝及其附近区域产生了明显的拉应力集中。

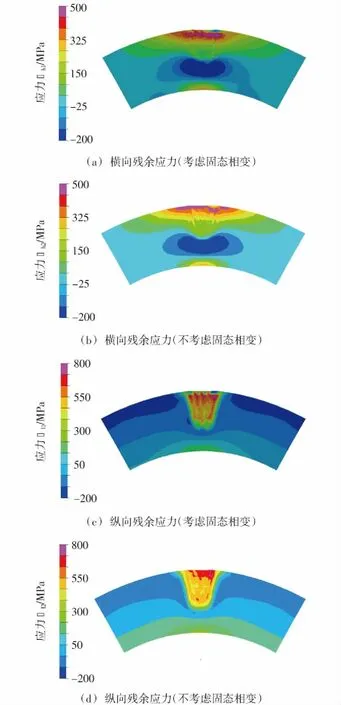
图8 P91钢补焊试件横截面残余应力分布云图

图9给出了补焊件中心横断面上表面应力分布曲线。对于横向应力来说，考虑和不考虑固态相变效应时，两者的分布特征相似但在应力值方面存在差异。考虑固态相变时，末道焊缝产生了明显的压应力，应力值为-93 MPa。不考虑固态相变时，熔合区两侧产生了明显的拉应力集中，应力数值分别为543 MPa，490 MPa。对于纵向应力，不考虑固态相变时纵向应力在熔合区产生了明显的拉应力集中，应力数值为718 MPa。考虑固态相变时，纵向应力在末道焊缝处表现为明显的压应力，其值为-155 MPa。另外，图9中还给出了中央横断面上表面的残余应力计算结果与试验测量结果对比。从图中可知，试验结果与考虑固态相变下的计算结果吻合较好。从而证明了文中所建三维有限元模型的有效性。

图9 沿补焊件中心横断面上表面应力分布

工程结构常用的合金结构钢焊接及热影响区的纵向应力通常为较大的拉应力。文中补焊结构末道焊缝及其附近的热影响区为压应力，这是由于焊接电弧作用末道焊缝及其热影响区金属被加热至Ac1温度以上，该部分金属加热过程中被奥氏体化，在冷却中完全转化为马氏体，体积发生膨胀，因而会在末道焊缝及其热影响区表现为压应力。压应力能够有效防止焊接冷裂纹及应力腐蚀裂纹的产生。

4 结论

(1)建立考虑固态相变条件下P91钢同质补焊残余应力的三维有限元数值分析模型，对P91钢多层多道补焊残余应力进行了模拟计算，计算结果较好地说明了固态相变对补焊残余应力分布特征的影响，为实际补焊工艺的制定及补焊材料的选择提供了研究基础。

(2)数值模拟结果显示由马氏体相变引起的材料力学性能变化、体积变化及相变塑性对补焊残余应力的影响显著，使得补焊结构熔合区表面的横向应力为压应力，纵向应力表现为拉应力和压应力交错分布的特征。横向应力和纵向应力大小分别为-93 MPa，-155 MPa。

(3)P91钢同质补焊结构件残余应力计算结果于试验测量结果吻合较好，说明了在有限元模型中考虑固体相变对残余应力的影响能够较好地反映P91补焊结构的真实应力状态。也验证了文中所建P91钢多层多道同质补焊三维有限元模型的有效性。