马赫数离散方式对吻切锥变马赫数乘波飞行器构型和气动性能的影响

2020-12-28赵振涛黄伟金宏盛王宏董媛平

航空学报 2020年12期

赵振涛，黄伟，金宏盛，王宏，董媛平

1. 中国人民解放军96755部队 260分队，通化 134000 2. 国防科技大学高超声速冲压发动机技术重点实验室，长沙 410073

空天飞行器是一种以涡轮基组合循环发动机(TBCC)/火箭基组合循环发动机(RBCC)为主动力的、能够在大气层内和大气层外长时间飞行、可重复使用、长期在轨并能够进行轨道机动的飞行器[1]。其飞行速域宽、飞行空域大，气动外形需要同时考虑起飞时的高升力与超/高超声速时的高升阻比需求，这对飞行器气动布局设计提出了新的挑战。为了有效解决上述问题，国内外学者开展了一系列的研究。刘晓斌等以水平起降高超声速飞行器的总体装载和动力系统需求为基础，完成了一种双向飞翼空天飞行器的概念外形设计[2]。焦子涵等利用伸缩翼布局和翻转翼布局两种变形方式，设计了一种将高超声速巡航性能和低速起降性能相匹配的全速域可变形飞行器[3]。

此外，以乘波飞行器设计方法为基础，开展具有宽速域、大空域飞行性能的飞行器气动布局设计也是一种解决问题的思路，并成为了当前的研究热点之一。王发民等利用组合拼接式的方法将高设计马赫数的乘波飞行器与低设计马赫数的乘波飞行器相结合，设计了一款宽速域乘波飞行器[4]。借鉴该组合设计思想，李世斌等也开展了乘波飞行器的组合设计研究，提出了“串联式”与“并联式”的两种宽速域乘波飞行器设计方法[5-6]。类似地，Corda将多个具有不同设计马赫数的乘波飞行器结合，设计了一种具有多重设计马赫数的星型乘波飞行器构型[7]。注意到理想乘波飞行器在亚声速下的升阻比可以很小，所以Takama提出了一种将外翼附加到理想乘波飞行器上的设计方案，以期改善理想乘波飞行器的低速气动特性[8]。

不同于上述设计方案，刘传振等根据吻切锥乘波飞行器的设计几何关系，提出了双后掠乘波飞行器的设计概念，为宽速域乘波飞行器气动构型的设计提供了新的思路[9]。在此基础上，赵振涛等提出了设计曲线(进气捕获曲线(Inlet Capture Curve，ICC)和流动捕获管(Flow Capture Tube，FCT))更为灵活时的两种吻切锥定后掠乘波飞行器的设计方法，分别命名为尖头乘波飞行器和三角翼乘波飞行器设计方法，并对它们的低速气动性能情况进行了分析[10-11]。结合变形技术，戴佩等提出了一种变后掠翼的宽速域乘波飞行器设计方法，并对其气动性能进行了分析[12]。另一方面，考虑到飞行器的外形(尤其是平面外形)对飞行器的气动和操纵特性有较大的影响，刘传振等将双后掠乘波飞行器这一概念进行了拓展，提出了定平面形状乘波飞行器的设计理念[13-15]。

除了上述几种宽速域乘波飞行器设计方法以外，变马赫数乘波飞行器设计方法也是一类重要的宽速域乘波飞行器设计方法。将其和不同的乘波飞行器展向设计理论结合可以得出相应的宽速域乘波飞行器设计方法。李世斌等将锥导乘波飞行器设计理论与变马赫数乘波飞行器设计方法相结合，提出了锥导变马赫数乘波飞行器设计方法[16-17]；赵振涛等将其与吻切锥乘波飞行器设计方法结合，提出了吻切锥变马赫数乘波飞行器(Osculating Cone Variable Mach number WaveRider，OCVMWR)设计方法[18]；类似地，柳军等利用吻切流场乘波飞行器设计理论对变马赫数乘波飞行器设计方法进行了相关的研究[19]。这些研究均在不同程度上提高了乘波飞行器在非设计条件下的气动性能，使其可以更好地适应从起飞爬升到高空高速巡航的这一全速域、大空域的飞行环境[20]。但以乘波飞行器设计方法为基础的宽速域高超声速飞行器的研究仍有很多内容需要进一步深入。

本文研究了在给定的设计马赫数区间内，马赫数离散方式对吻切锥变马赫数宽速域乘波飞行器构型和气动性能的影响，对吻切锥变马赫数宽速域乘波飞行器设计方法进一步深入研究，有利于加深人们对这一种宽速域乘波飞行器设计方法的认识水平。

1 设计马赫数区间的离散方式

吻切锥变马赫数乘波飞行器设计方法是一种将变马赫数乘波飞行器设计方法与吻切锥设计理论相结合的宽速域乘波飞行器设计方法。与常规吻切锥乘波飞行器设计方法的主要区别是：在OCVMWR的基准流场中，每一个吻切平面内的圆锥流场均具有不同的设计马赫数。这一独特的设计使OCVMWR比普通的吻切锥乘波飞行器能够更好地兼顾多种飞行状态以进行宽速域飞行[18]。文献[18]详细地介绍了基于吻切锥理论的变马赫数“并联”宽速域乘波飞行器设计方法，即OCVMWR设计方法。为了更好地介绍采用的设计马赫数区间离散方法，首先对文献[18]中提出的设计马赫数区间的离散方法进行简单回顾。

如图1所示，在给定的ICC曲线中，取出足够密的n个离散点，标号为0～n-1。其中，曲线部分有m个离散点，标号为0～m-1，直线部分有n-m个离散点，标号为m～n-1，离散点m-1即是ICC的直线段与曲线段间的交界点；j为ICC曲线段上的任意一离散点。因为ICC边缘处曲率变化较大，所以为了更好地生成乘波飞行器的几何外形，在ICC曲线段的边缘处加密取点。

根据给定的设计马赫数区间[Mamin,Mamax]，以等差数列的分布规律为每一离散点处的吻切平面配置相应的设计马赫数。即设离散点1处的设计马赫数为Mamin，离散点m-2处的设计马赫数为Mamax，则其中的第j个离散点的设计马赫数可由式(1)确定：

图1 OCVMWR生成方法中采用的马赫数离散方法Fig.1 Mach number discrete method in OCVMWR generation method

1≤j≤m-2

(1)

由于离散点0的三维坐标已由设计参数确定，所以不需要为其匹配设计马赫数。此外，考虑到前体与进气道一体化设计对进气道进口气流均匀性的要求，ICC中的直线段部分没有进行变马赫数设计，而是将直线段的各离散点处的设计马赫数保持一致，均取为Mam-2。如此设置也可确保乘波飞行器构型直线段部分与曲线段部分之间的光滑过渡。

为了分析在给定的设计马赫数区间内，设计马赫数的离散方式对OCVMWR形状和气动性能的影响，在文献[18]提出的离散方法的基础上设计了多种不同的离散方式。为使这些离散方式具有代表性，从函数的(非)线性、单调性、凹凸性3个方面出发，选取了线性递减函数、正弦函数、余弦函数、1-正弦函数、1-余弦函数作为给定的设计马赫数区间离散方法，这些函数图象如图2所示。离散方法的具体形式如下：

1) 线性递减函数离散方法

设离散点1处的设计马赫数为Mamax，离散点m-2处的设计马赫数为Mamin，则其中的第j个离散点的设计马赫数为

1≤j≤m-2

(2)

利用线性递减离散方法生成的OCVMWR称为线性递减OCVMWR(Linear Decreasing Function OCVMWR，LDF-OCVMWR)。

2) 正弦函数离散方法

设离散点1处的设计马赫数为Mamin，离散点m-2处的设计马赫数为Mamax，则其中的第j个离散点的设计马赫数为

(3)

利用正弦函数离散方法生成的OCVMWR称为正弦函数OCVMWR(Sine Function OCVMWR，SF-OCVMWR)。

3) 余弦函数离散方法

设离散点1处的设计马赫数为Mamax，离散点m-2处的设计马赫数为Mamin，则其中的第j个离散点的设计马赫数为

1≤j≤m-2

(4)

图2 离散方法中的初等函数图象Fig.2 Image of elementary functions in discrete methods

利用余弦函数离散方法生成的OCVMWR称为余弦函数OCVMWR(Cosine Function OCVMWR，CF-OCVMWR)。

4) 1-正弦函数离散方法

设离散点1处的设计马赫数为Mamax，离散点m-2处的设计马赫数为Mamin，则其中的第j个离散点的设计马赫数为

(Mamax-Mamin) 1≤j≤m-2

(5)

利用1-正弦函数离散方法生成的OCVMWR称为1-正弦函数OCVMWR(1-Sine Function OCVMWR，1-SF-OCVMWR)。

5) 1-余弦函数离散方法

设离散点1处的设计马赫数为Mamin，离散点m-2处的设计马赫数为Mamax，则其中的第j个离散点的设计马赫数为

(Mamax-Mamin) 1≤j≤m-2

(6)

利用1-余弦函数离散方法生成的OCVMWR称为1-余弦函数OCVMWR(1-Cosine Function OCVMWR, 1-CF-OCVMWR)。

为增强统一性与对比性，将文献[18]中采用的马赫数离散方法称为线性递增离散方法，并将由其生成的OCVMWR称为线性递增OCVMWR(Linear Increasing Function OCVMWR，LIF-OCVMWR)。

2 吻切锥变马赫数乘波飞行器几何模型

根据第1节提出的5种马赫数离散方法，利用吻切锥变马赫数乘波飞行器设计方法得到了5个应用实例。利用控制变量的思想生成的5个应用实例的设计参数均与文献[18]中应用实例的设计参数保持一致，即它们的设计参数都是相同的，相互间的区别仅在于采用的马赫数离散方式不同。与文献[18]中相同，采用式(7)与式(8)作为OCVMWR设计的ICC与FCT，相应的设计参数由表1详细地列出。图3给出了利用6种马赫数离散方法生成的OCVMWR几何模型，它们的几何参数由表2详细地列出，为了对比需要，包括了文献[18]中生成的线性递增OCVMWR的设计实例。

表1 具有不同马赫数离散方式的OCVMWR设计参数

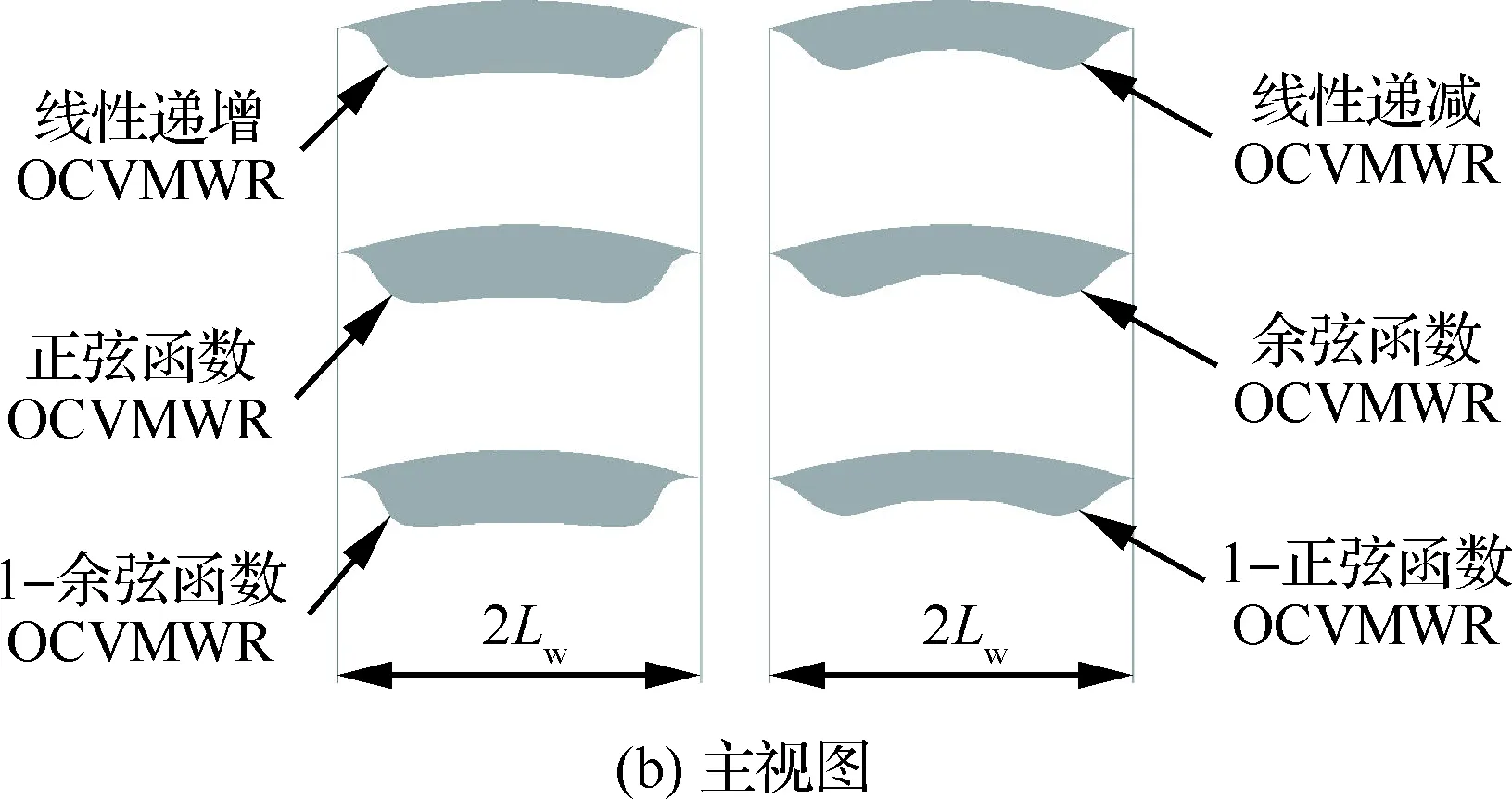
图3 6种不同的马赫数离散方法生成的OCVMWR的几何模型对比Fig.3 Comparison of geometric models of OCVMWR generated by six different Mach number discrete methods

表2 应用实例的几何参数Table 2 Geometric parameters for application examples

ICC为

(7)

式中：a为激波出口型线方程系数。

FCT为

x=R0+A0y2

(8)

式中：A0为抛物线的系数。

3 马赫数离散方式对OCVMWR几何构型的影响

3.1 (非)线性对几何构型的影响

如图2所示，分析离散方法中函数的线性与非线性对OCVMWR气动外形的影响可以通过对比线性递增OCVMWR、正弦函数OCVMWR以及1-余弦函数OCVMWR气动外形的差异获得，也可以通过对比线性递减OCVMWR、余弦函数OCVMWR以及1-正弦函数OCVMWR气动外形的差异获得。

线性递增OCVMWR、正弦函数OCVMWR以及1-余弦函数OCVMWR离散方法的共同特点是它们的单调性均是递增的。如图4所示，线性递增OCVMWR的布局形状与正弦函数OCVMWR(1-余弦函数OCVMWR)的几何形状是不同的。具体来说，通过OCVMWR设计参数的设置，保证了线性递增OCVMWR构型与正弦函数OCVMWR(1-余弦函数OCVMWR)构型在边缘处和中间处的一致性，而它们的主要差异则是在ICC的曲线段对应的部分。

图4 线性递增OCVMWR、正弦函数OCVMWR及1-余弦函数OCVMWR几何构型对比Fig.4 Comparison of geometric models of LIF-OCVMWR, SF-OCVMWR and 1-CF-OCVMWR

同时，需要注意的是，正弦函数OCVMWR与线性递增OCVMWR的构型差异和1-余弦函数OCVMWR与线性递增OCVMWR的构型差异是不同的，即线性递增OCVMWR的构型包含1-余弦函数OCVMWR的构型，而被正弦函数OCVMWR的构型包含，这从表2中相应应用实例的体积参数中也可看出。这体现了离散方法的凹凸性对OCVMWR构型的影响，这部分内容将在第3.3节中展开说明。

线性递减OCVMWR、余弦函数OCVMWR以及1-正弦函数OCVMWR离散方法的共同特点是它们的单调性均是递减的。如图5所示，它们之间的构型差异情况是：线性递减OCVMWR构型包含1-正弦函数OCVMWR构型，而被余弦函数OCVMWR构型包含。注意到，1-正弦函数OCVMWR和1-余弦函数OCVMWR的离散方法具有相同的凹凸性，并且余弦函数OCVMWR和正弦函数OCVMWR的离散方法具有相同的凹凸性。由此可知，在单调性相同的情况下，离散方法是线性的OCVMWR包含非线性的具有凹函数性质的OCVMWR，而被非线性的具有凸函数性质的OCVMWR包含。

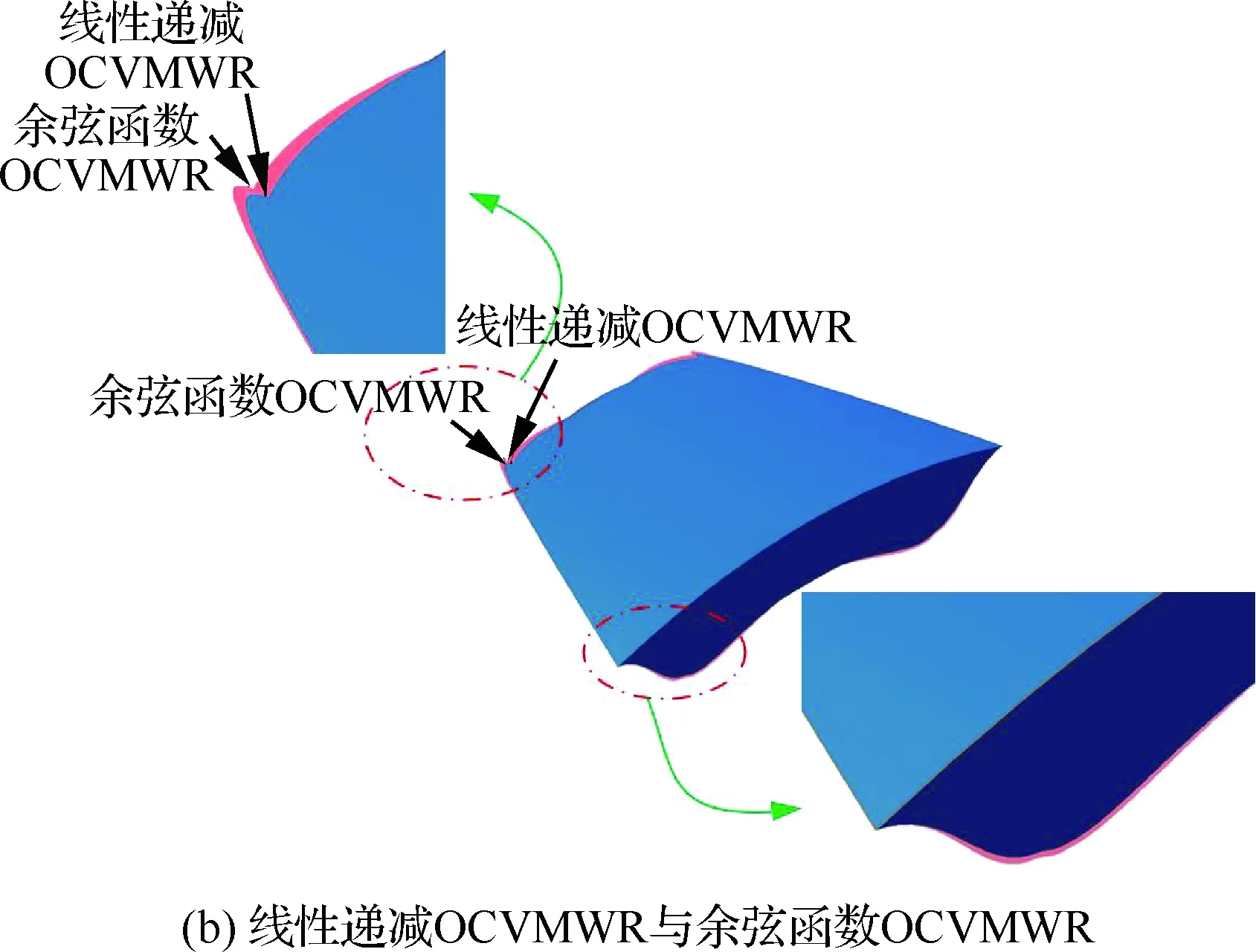
图5 线性递减OCVMWR、余弦函数OCVMW及1-正弦函数OCVMWR几何构型对比Fig.5 Comparison of geometric models of LDF-OCVMWR, CF-OCVMWR and 1-SF-OCVMWR

3.2 单调性对几何构型影响

如图2所示，离散方法的单调性对OCVMWR构型布局的影响可通过分析线性递增OCVMWR与线性递减OCVMWR之间的构型差异、正弦函数OCVMWR与余弦函数OCVMWR之间的构型差异以及1-正弦函数OCVMWR与1-余弦函数OCVMWR之间的构型差异得到。

如图6(a)所示，从整体上看，线性递增OCVMWR构型更长、更厚一些，而线性递减OCVMWR构型则更宽一些；而且从OCVMWR构型的边缘处至中间处这一过程中，线性递增OCVMWR构型的前缘线是光滑过渡的，而线性递减OCVMWR构型的前缘线则出现了尖点，没有光滑过渡。

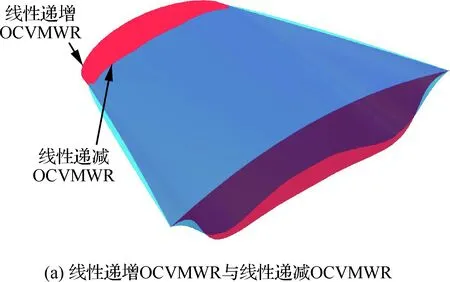
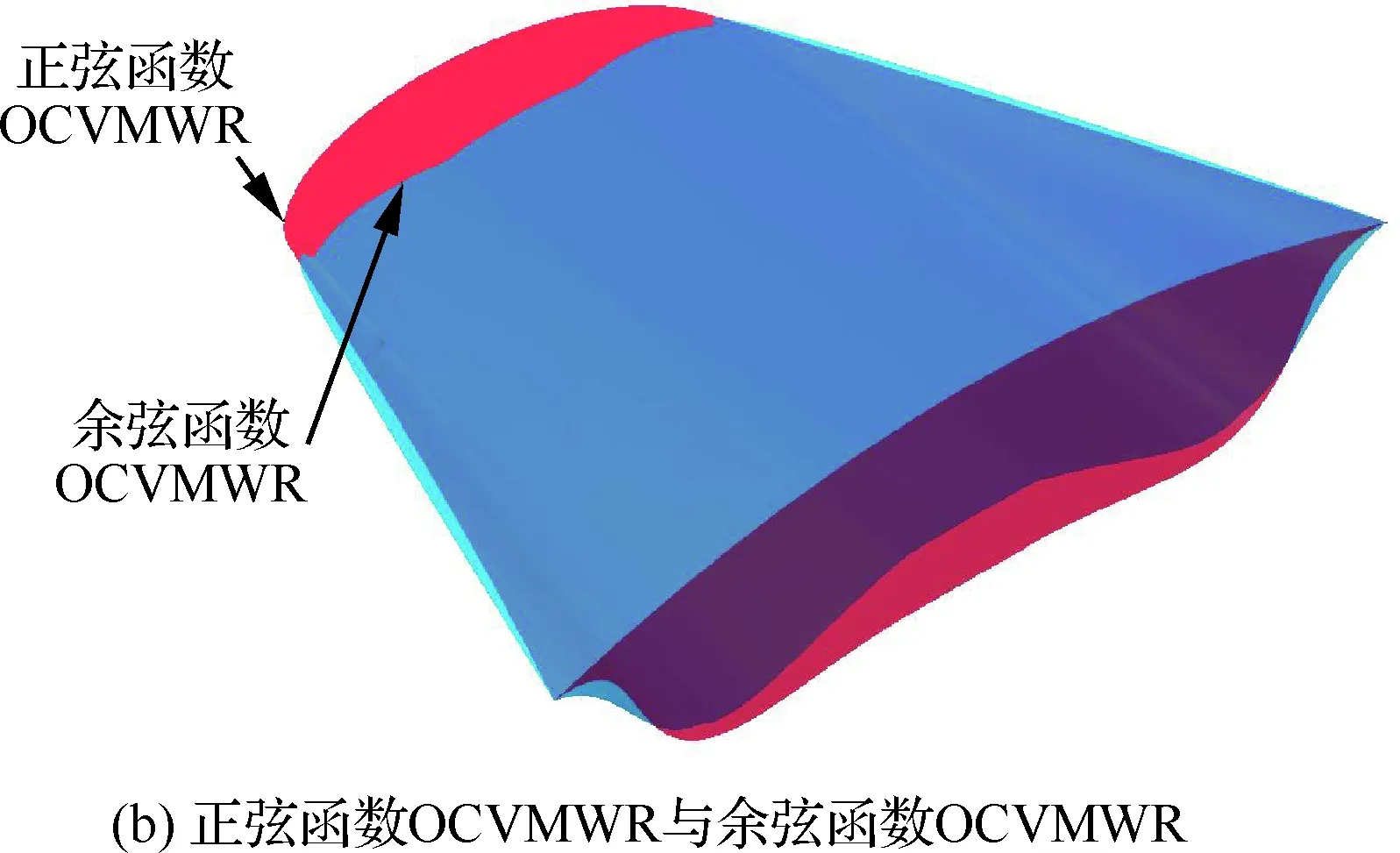
图6 具有不同单调性离散方法生成的OCVMWR几何构型对比Fig.6 Comparison of geometric models of OCVMWR generated by discrete methods with different monotonicity

图6(b)与图6(c)所示为正弦函数OCVMWR(1-余弦函数OCVMWR)和余弦函数OCVMWR(1-正弦函数OCVMWR)之间的构型差异情况，可见与线性递增OCVMWR和线性递减OCVMWR构型间的差异情况基本上是一致的，只是在相应的幅度上有所区别。由此可知，在其他条件相同的情况下，离散方法具有单调递增性质的OCVMWR构型在构型中间处比具有单调递减性质的OCVMWR构型更长、更厚一些，而在构型边缘处则更窄一些。

此外，线性递增OCVMWR与线性递减OCVMWR构型在底面处的宽度是相同的，这是由设计参数Lw控制的；在构型的中间处，线性递增OCVMWR构型的长度更长，这主要是由于其中间位置处的设计马赫数为高马赫数，而在构型的边缘处，线性递减OCVMWR构型更宽一些；在高度方向，两构型的下表面在展向的某一位置处相交，这主要是由于线性递增OCVMWR和线性递减OCVMWR在构型的中间处和边缘处的设计马赫数相反造成的。

3.3 凹凸性对几何构型的影响

如图2所示，通过对比正弦函数OCVMWR与1-余弦函数OCVMWR的构型布局差异以及余弦函数OCVMWR与1-正弦函数OCVMWR的构型布局差异，可以分析离散方法的凹凸性对OCVMWR构型布局的影响情况。

如图7(a)所示，在具有相同非线性和相同单调性的情况下，离散方法具有凸函数性质的正弦函数OCVMWR构型包含具有凹函数性质的1-余弦函数OCVMWR的构型，即离散方法具有凸函数性质的正弦函数OCVMWR构型体积更大一些，这一点从表2中的体积参数也可看出。此外，正弦函数OCVMWR构型的容积率也更大一些。

图7 具有不同凹凸性的离散方法生成的OCVMWR几何构型对比Fig.7 Comparison of geometric models of OCVMWR generated by discrete methods with different concavity and convexity

上述结论对于离散方法具有凸函数性质的余弦函数OCVMWR构型和具有凹函数性质的1-正弦函数OCVMWR构型也是成立的，如图7(b)所示。由此可知，在其他条件相同的情况下，离散方法具有凸函数性质的OCVMWR构型包含具有凹函数性质的OCVMWR的构型，具有更大的容积率。

第3节分析了离散方法的不同性质(包括(非)线性、单调性以及凹凸性)对OCVMWR几何构型的影响。总体上来说，与其他性质相比，离散方法的单调性对OCVMWR几何构型的影响最大。

4 马赫数离散方式对OCVMWR气动性能的影响

利用商业CFD软件ANSYS Fluent对在第2节中生成的6种OCVMWR构型进行了黏性数值模拟，分析马赫数离散方式对OCVMWR构型气动性能的影响。

在数值计算中，选取给定的设计马赫数区间内4.0、6.0、8.0、10.0作为飞行马赫数，设置飞行攻角分别为-2°、0°、2°、4°、6°、8°、10°，来流条件为25 km高空的大气条件，静压设置为2 511.01 Pa，静温为221.65 K，采用理想气体假设，壁面条件为绝热无滑移条件。

4.1 (非)线性对气动性能的影响

与第3.1节相似，离散方法的(非)线性对OCVMWR构型气动性能的影响既可通过对比分析线性递增OCVMWR、正弦函数OCVMWR以及1-余弦函数OCVMWR之间的气动性能差异获得，也可以通过对比分析线性递减OCVMWR、余弦函数OCVMWR以及1-正弦函数OCVMWR之间的气动性能差异获得。

图8给出了线性递增OCVMWR、正弦函数OCVMWR和1-余弦函数OCVMWR在不同飞行马赫数下的气动性能情况。可以看出，在同一飞行马赫数下，3种OCVMWR的升力系数与阻力系数均随攻角的增加而增大，升阻比随攻角的增大而减少，这是符合OCVMWR的气动特性的[18]。在不同飞行马赫数下，除飞行攻角为-2°、飞行马赫数为8.0和10.0这两种飞行工况外，线性递增OCVMWR的升阻比均小于1-余弦函数OCVMWR，而大于正弦函数OCVMWR。同时，正弦函数OCVMWR和1-余弦函数OCVMWR升阻比之间的差异即是由于离散方法的凹凸性不同造成的。此外，在阻力系数方面，除飞行攻角为10°、飞行马赫数为4.0这一飞行工况外，线性递增OCVMWR的阻力系数均小于正弦函数OCVMWR，而大于1-余弦函数OCVMWR。但这3种OCVMWR的升力系数则不具有类似的规律性。

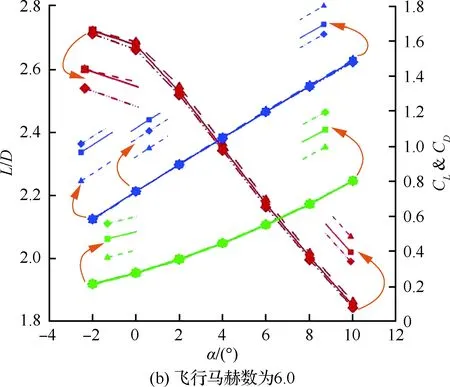
图8 线性递增OCVMWR、正弦函数OCVMWR和1-余弦函数OCVMWR气动特性随攻角的变化情况Fig.8 Changes of aerodynamic performance of LIF-OCVMWR, SF-OCVMWR and 1-CF-OCVMWR versus angle of attack

图9给出了线性递减OCVMWR、余弦函数OCVMWR和1-正弦函数OCVMWR在不同飞行马赫数下的气动性能情况。可以看出，在每一飞行马赫数下，线性递减OCVMWR的升阻比均小于1-正弦函数OCVMWR，而大于余弦函数OCVMWR。在此，对比考虑线性递增OCVMWR、正弦函数OCVMWR和1-余弦函数OCVMWR可以发现，1-正弦函数OCVMWR与1-余弦函数OCVMWR的离散方法具有相同的凹凸性，余弦函数OCVMWR与正弦函数OCVMWR具有相同的凹凸性。由此可知，在单调性相同的情况下，离散方法是线性的OCVMWR的升阻比大于非线性的具有凸函数性质的OCVMWR，而小于非线性的具有凹函数性质的OCVMWR的升阻比。

在升力系数方面，如图9所示，线性递减OCVMWR的升力系数均小于1-正弦函数OCVMWR，而大于余弦函数OCVMWR。但这3

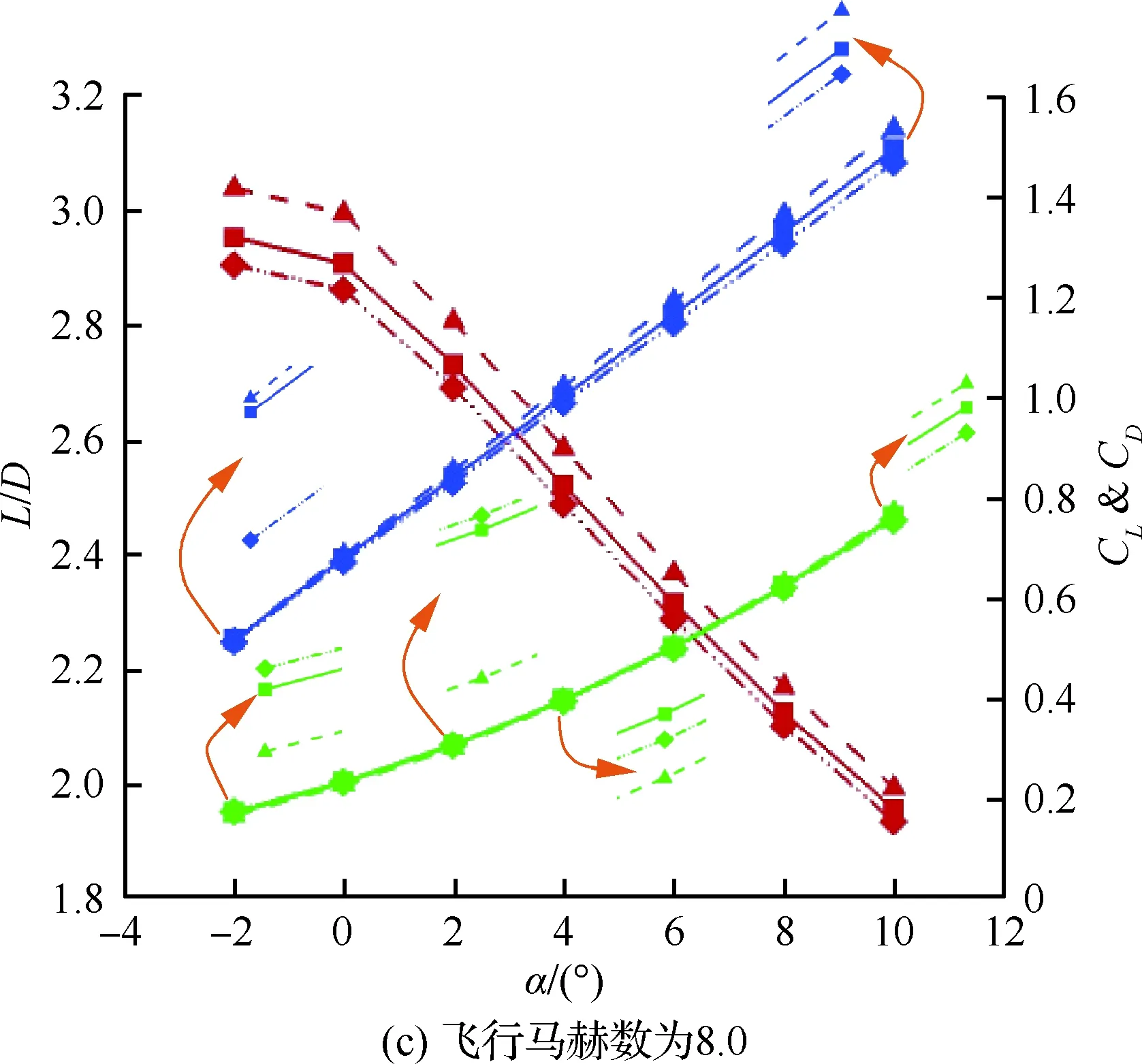
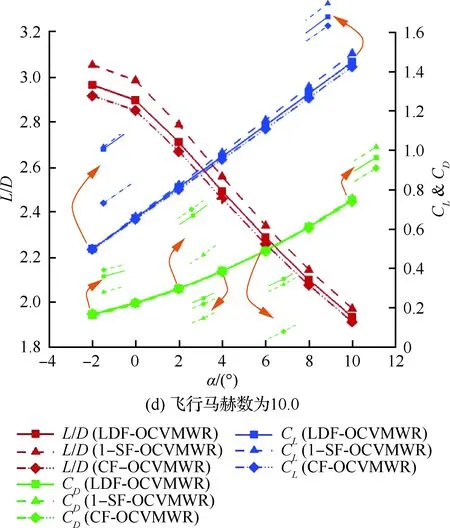
图9 线性递减OCVMWR、余弦函数OCVMWR和1-正弦函数OCVMWR气动特性随攻角的变化情况Fig.9 Changes of aerodynamic performances of LDF-OCVMWR, CF-OCVMWR and 1-SF-OCVMWR versus angle of attack

种OCVMWR的阻力系数则不具有类似的规律性。这里的升、阻力系数的规律性和线性递增OCVMWR、正弦函数OCVMWR与1-余弦函数OCVMWR之间的升、阻力系数的规律性是不同的，其差异是由离散方法的单调性造成的。

此外，对比图8与图9可以看出，线性递减OCVMWR、余弦函数OCVMWR和1-正弦函数OCVMWR三者之间的升阻比偏差是大于线性递增OCVMWR、正弦函数OCVMWR和1-余弦函数OCVMWR三者之间的升阻比偏差的。这也反映出离散方法的单调性对OCVMWR气动性能的影响更为明显。

4.2 单调性对气动性能的影响

图10～图12分别对比地给出了线性递增OCVMWR与线性递减OCVMWR、正弦函数OCVMWR与余弦函数OCVMWR以及1-正弦函数OCVMWR与1-余弦函数OCVMWR之间的气动特性情况。可以看出，在升阻比方面，离散方法是单调递减的OCVMWR的升阻比均大于离散方法是单调递增的OCVMWR。升力系数方面，在小攻角时，单调递减的OCVMWR总是低于单调递增的OCVMWR的，而在大攻角时却相反。此外，与单调递增的OCVMWR相比，单调递减的OCVMWR总是具有更低的阻力系数。

图10 线性递增OCVMWR和线性递减OCVMWR气动特性随攻角的变化情况Fig.10 Changes of aerodynamic performances of LIF-OCVMWR and LDF-OCVMWR versus angle of attack

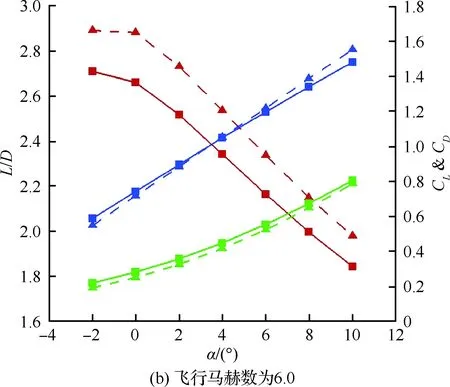
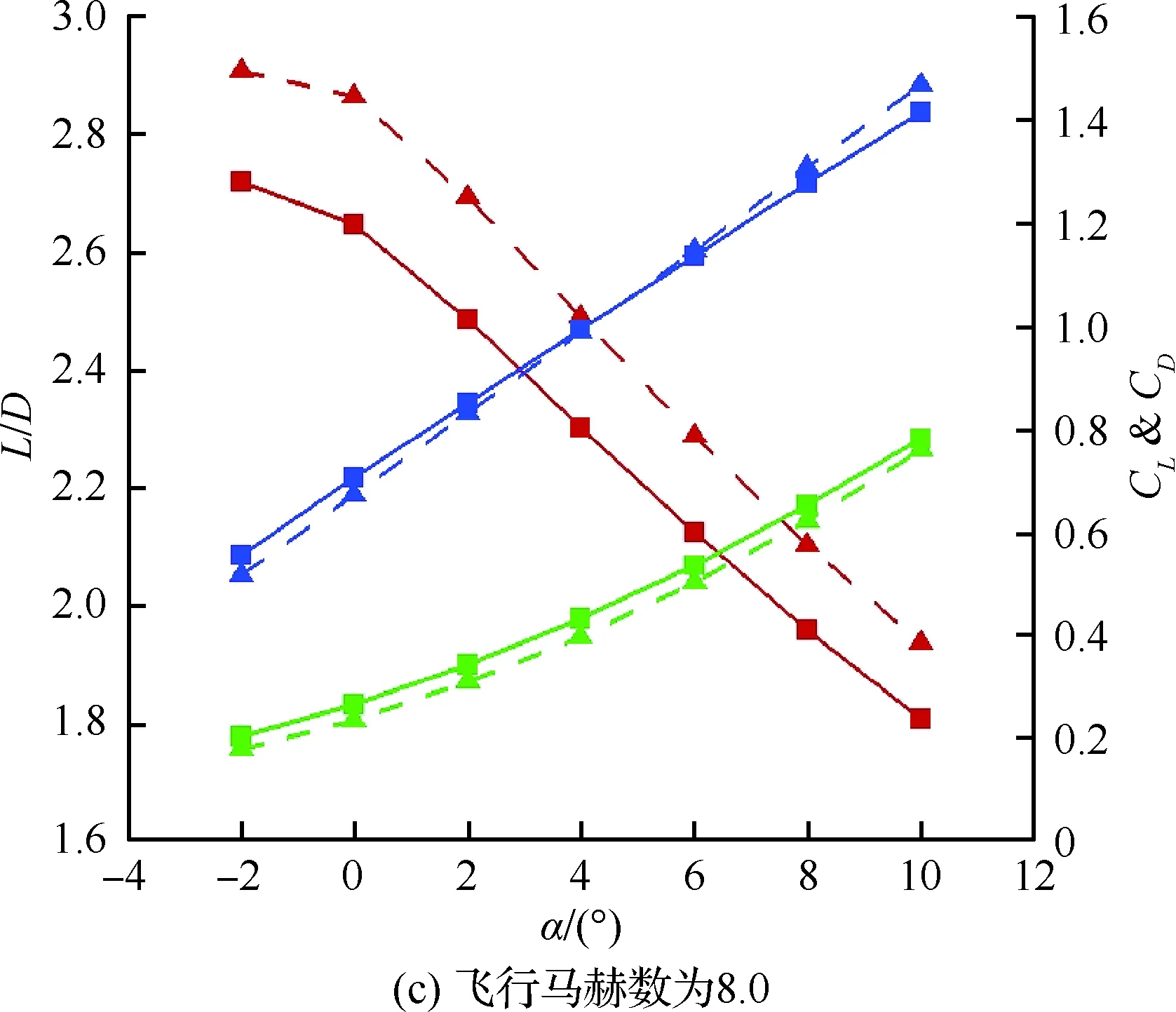
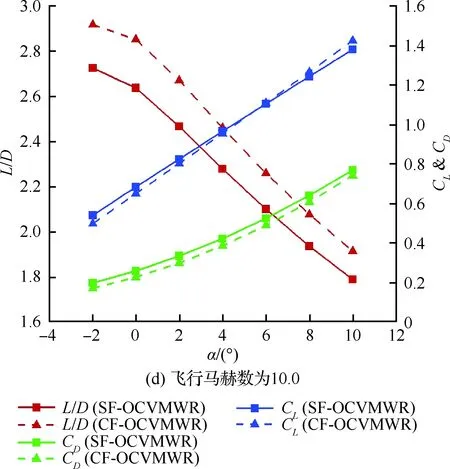
图11 正弦函数OCVMWR和余弦函数OCVMWR气动特性随攻角的变化情况Fig.11 Changes of aerodynamic performances of SF-OCVMWR and CF-OCVMWR versus angle of attack

4.3 凹凸性对气动性能的影响

类似于第3.3节，通过对比正弦函数OCVMWR(余弦函数OCVMWR)与1-余弦函数OCVMWR(1-正弦函数OCVMWR)的气动特性差异情况，可以分析离散方法的凹凸性对OCVMWR气动特性的影响情况。

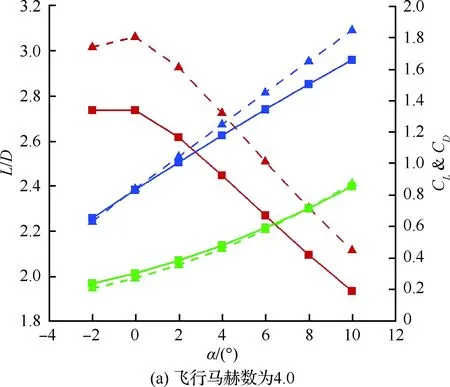
图12 1-余弦函数OCVMWR和1-正弦函数OCVMWR气动特性随攻角的变化情况Fig.12 Changes of aerodynamic performances of 1-CF-OCVMWR and 1-SF-OCVMWR versus angle of attack

实际上，图8与图9已经给出了它们之间的气动性能对比情况，即在升阻比方面，除飞行攻角为-2°、飞行马赫数为8.0和10.0这两种飞行工况外，1-余弦函数OCVMWR的升阻比均大于正弦函数OCVMWR；而在所有飞行工况下，1-正弦函数OCVMWR的升阻比均大于余弦函数OCVMWR；在升力系数方面，1-正弦函数OCVMWR的升力系数均大于余弦函数OCVMWR，而1-余弦函数OCVMWR与正弦函数OCVMWR在升力系数相对大小方面则不具有类似的规律性。此外，在阻力系数方面，除飞行攻角为10°、飞行马赫数为4.0这一飞行工况外，正弦函数OCVMWR的阻力系数均大于1-余弦函数OCVMWR，而余弦函数OCVMWR与1-正弦函数OCVMWR在阻力系数相对大小方面则不具有类似的规律性。

注意到1-正弦函数OCVMWR与1-余弦函数OCVMWR的设计马赫数离散方法均具有凹函数性质，而正弦函数OCVMWR与余弦函数OCVMWR的离散方法均具有凸函数性质。由此可知，在其他条件保持相同的条件下，与离散方法具有凸函数性质的OCVMWR相比，离散方法具有凹函数性质的OCVMWR具有更高的升阻比。

第4节分析了离散方法的不同性质(包括(非)线性、单调性以及凹凸性)对OCVMWR气动性能的影响。总体上来说，与其他性质相比，离散方法的单调性对OCVMWR气动性能的影响最大。

5 流场特性分析

为进一步理解设计马赫数的离散方式对OCVMWR气动性能的影响情况，从第4节中选取了相应的典型算例进行流动特性分析可以发现，在不同飞行马赫数下，OCVMWR的各气动性能参数均随飞行攻角的变化具有类似的趋势，所以第5节选取在飞行马赫数为6.0、飞行攻角为6°条件下的飞行流场进行分析。

5.1 (非)线性对流场特性的影响

与第3.1、4.1节相似，在分析(非)线性的影响时，既可对比分析线性递增OCVMWR与正弦函数OCVMWR以及1-余弦函数OCVMWR，也可以对比分析线性递减OCVMWR与余弦函数OCVMWR以及1-正弦函数OCVMWR。选取线性递增OCVMWR、正弦函数OCVMWR和1-余弦函数OCVMWR的飞行流场进行流场特性分析。

图13给出了线性递增OCVMWR与正弦函数OCVMWR距其各自前端1/4、1/2、3/4处以及出口处横截面上的压力分布。可以看出，线性递增OCVMWR与正弦函数OCVMWR周围压力分布相差不大，并且在前缘处的溢流情况类似，这即体现了两者在气动性能上的差异较小，如图8所示；具体来说，两者在构型前部分上的差异大于后部分，即在距离前端1/4处，两者压力在构型边缘处存在一定的差异，在距离前端1/2处，两者压力在构型中间处存在一定的差异。实际上，距前端1/4、1/2处正是两者构型前缘处偏差较大的地方，如图4(a)和图4(b)所示。这正体现出了两者构型在前缘处的差异对其气动性能的影响。

图14给出了线性递增OCVMWR与1-余弦函数OCVMWR距其各自前端1/4、1/2、3/4处以及出口处横截面上的压力分布。可以看出，线性递增OCVMWR和1-余弦函数OCVMWR之间的压力分布差异情况与线性递增OCVMWR和正弦函数OCVMWR类似，在此不再赘述。

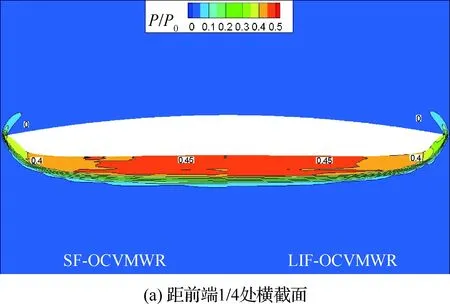
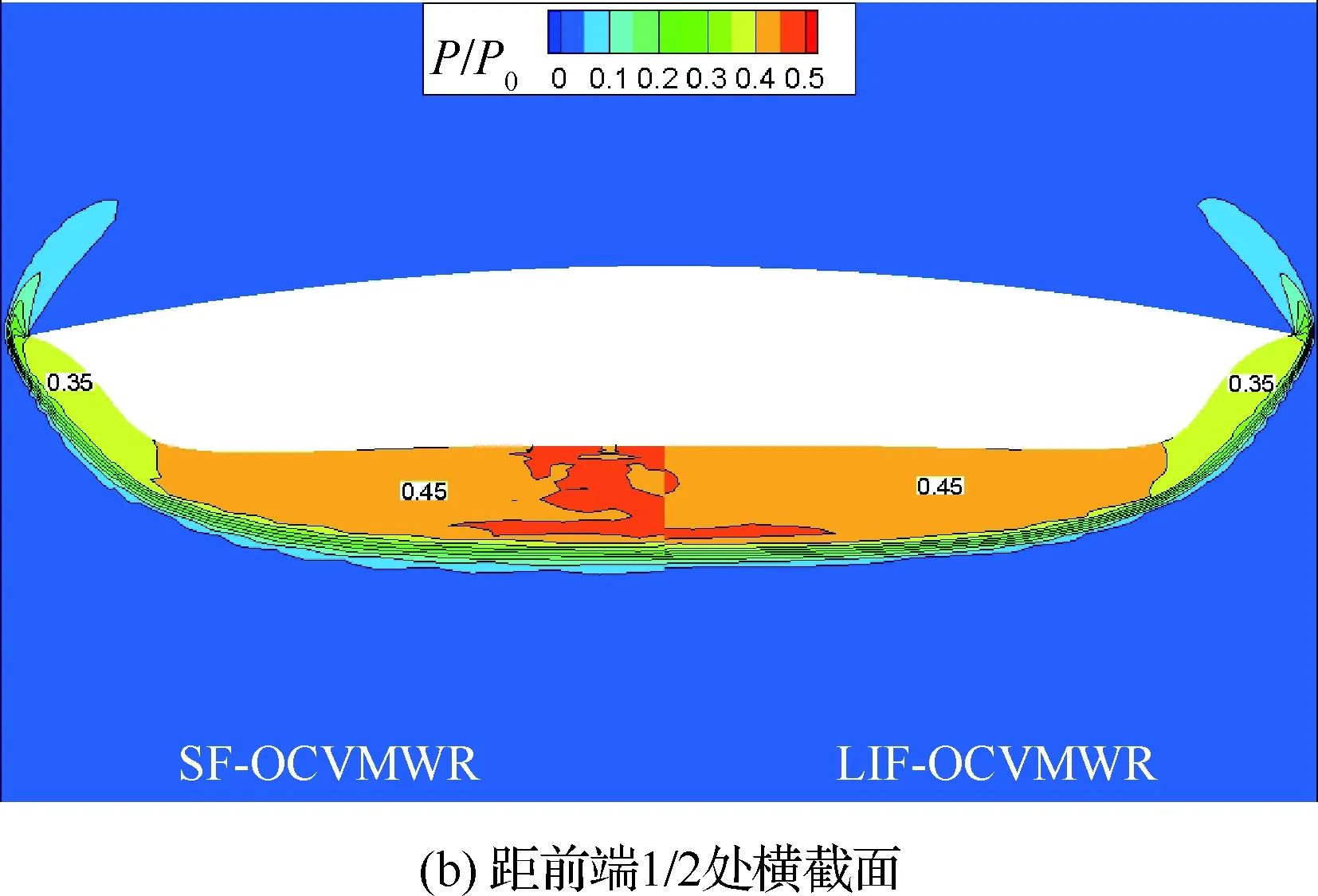
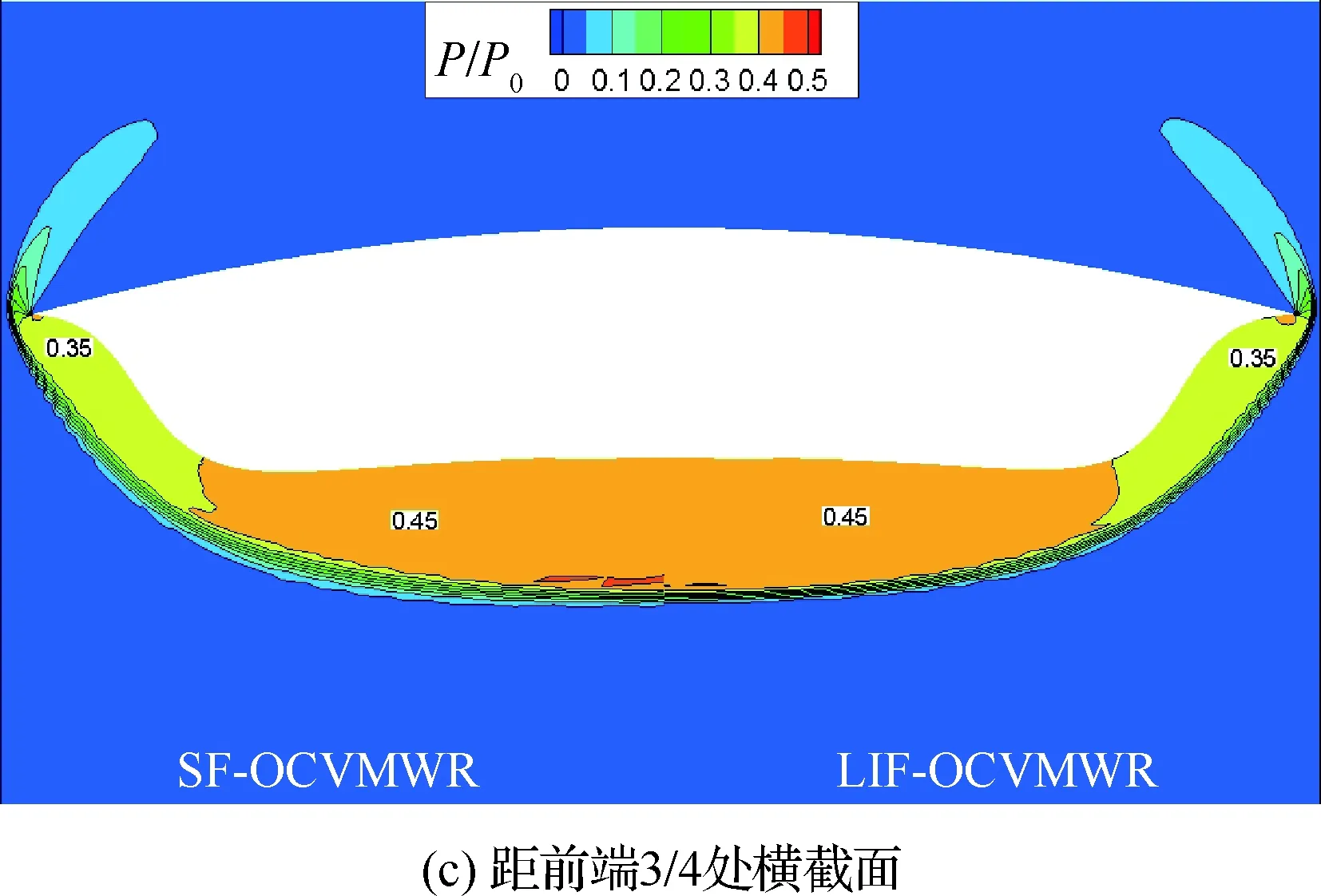
图13 线性递增OCVMWR和正弦函数OCVMWR不同横截面处的压力云图Fig.13 Pressure contour lines on different cross sections of LIF-OCVMWR and SF-OCVMWR

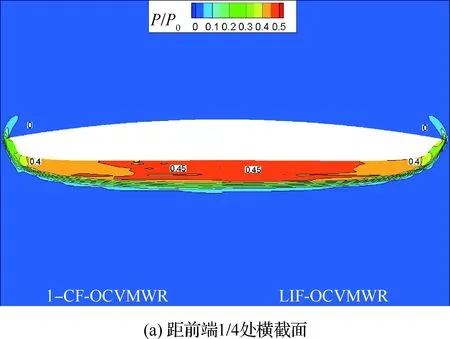
图14 线性递增OCVMWR和1-余弦函数OCVMWR不同横截面处的压力云图Fig.14 Pressure contour lines on different cross sections of LIF-OCVMWR and 1-CF-OCVMWR

5.2 单调性对流场特性的影响

选取正弦函数OCVMWR与余弦函数OCVMWR的飞行流场进行流场特性分析，进而研究单调性的影响。

图15给出了正弦函数OCVMWR与余弦函数OCVMWR距其各自前端1/4、1/2、3/4处以及出口处横截面上的压力分布。可以看出，两类OCVMWR的溢流情况相差不大，并且正弦函数OCVMWR下表面处的压力更大一些。但实际上，从图11中可以看出，在此飞行条件下，余弦函数OCVMWR的升阻比更大一些，这主要是由于其构型更薄一些。从气动系数的角度来看，相比于正弦函数OCVMWR，余弦函数OCVMWR的升力系数更大一些，而其阻力系数更小一些。

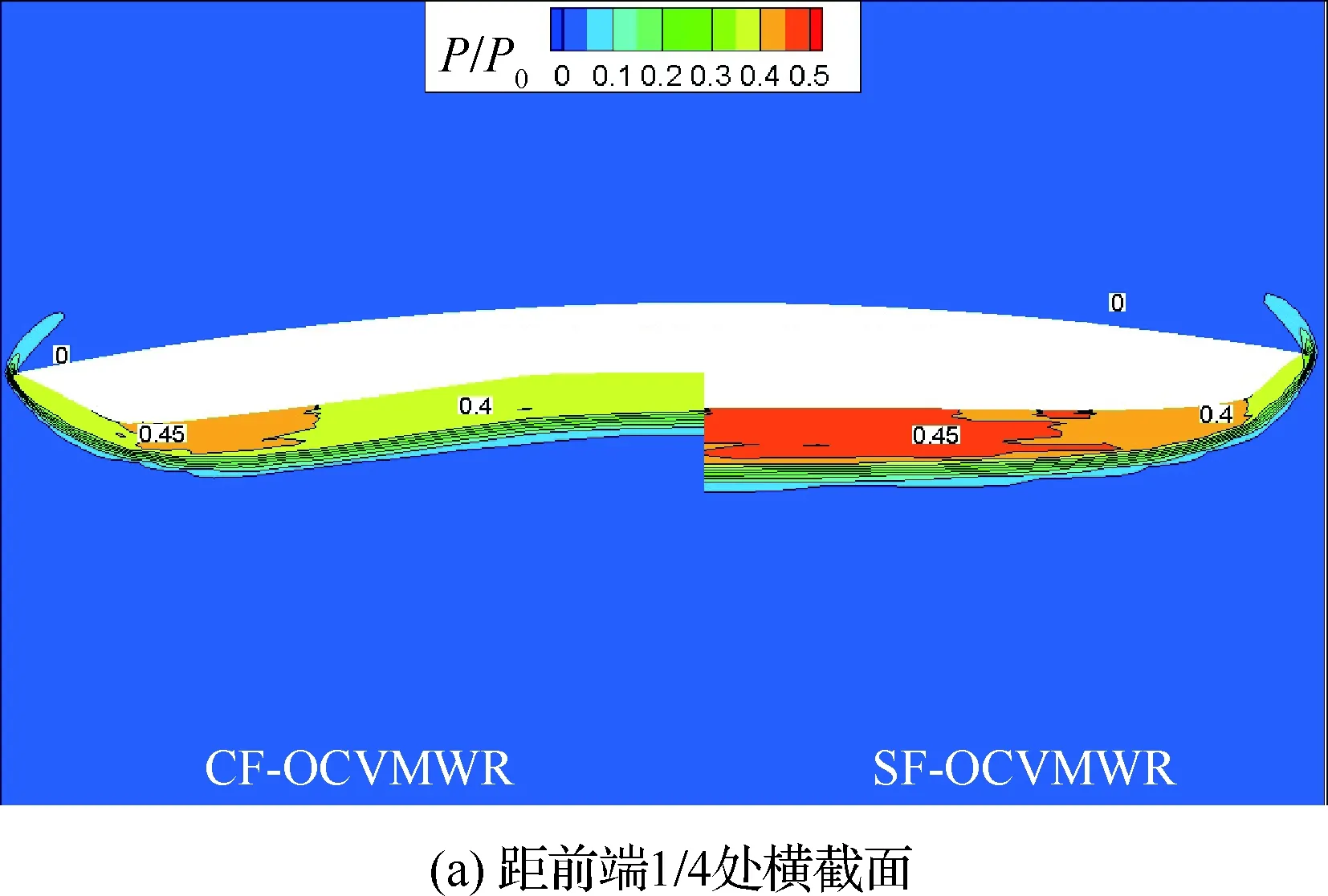
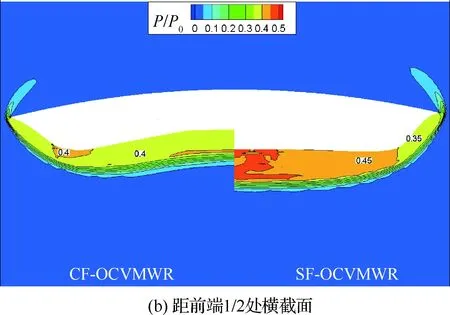
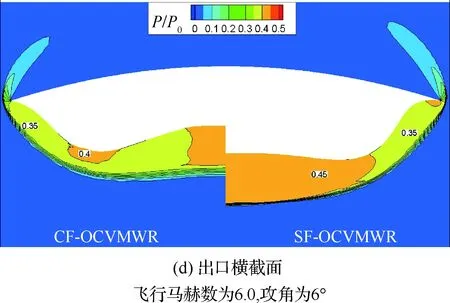
图15 正弦函数OCVMWR和余弦函数OCVMWR不同横截面处的压力云图Fig.15 Pressure contour lines on different cross sections of SF-OCVMWR and CF-OCVMWR

此外，从图15中也可看出，在不同横截面处，余弦函数OCVMWR的下表面中存在一压力较高的单独区域，而其原因在于从前缘处开始，余弦函数OCVMWR的下表面产生了一定的凹陷，从图16中也可以看出这一点。

图16 余弦函数OCVMWR和正弦函数OCVMWR下表面压力云图Fig.16 Pressure contour lines on lower surface of CF-OCVMWR and SF-OCVMWR

5.3 凹凸性对流场特性的影响

通过对比分析余弦函数OCVMWR和1-正弦函数OCVMWR的飞行流场之间的异同研究凹凸性的影响。图17给出了余弦函数OCVMWR和1-正弦函数OCVMWR距其各自前端1/4、1/2、3/4处以及出口处横截面上的压力分布。可以看出，压力在构型边缘处的差异在其前端更大一些，而构型后端的压力差异主要表现在截面的中间部分。