变循环发动机过渡态性能直接模拟方法
2020-12-28贾琳渊陈玉春程荣辉宋可染谭甜
贾琳渊,陈玉春,程荣辉,宋可染,谭甜
1. 西北工业大学 动力与能源学院,西安 710072 2. 中国航发沈阳发动机研究所,沈阳 110015
变循环发动机(Variable Cycle Engine,VCE)是军民用超声速巡航动力研究的热点。VCE通过变几何部件的调节,不仅可以获得更好的稳态性能,还能够有效地缩短过渡态过程时间、增加稳定裕度。但这一特点也增加了VCE过渡态性能模拟和控制规律设计的难度,特别是VCE的转模态过程一直是VCE研究的重点和难点。
国内外研究人员已经在VCE过渡态性能模拟和控制规律设计方面做了一定的研究工作。Przybylko和Rock[1]设计了GE23变循环发动机的多变量控制器,在发动机过渡态计算模型上验证了VCE过渡态过程多变量控制的可行性。唐海龙[2]和刘增文[3]等分别利用稳态计算模型对带有核心机驱动风扇(Core Driven Fan Stage,CDFS)的VCE的转模态过程进行了研究,给出了可行的变几何参数的调节规律。苟学中[4]给定了转模态过程变几何部件的调节规律实现了VCE转模态过程的动态模拟,但是转模态过程中出现了显著的超温、超转和喘振裕度的波动。周红等[5-7]研究了影响VCE转模态过程的关键参数,给出了变几何参数的一般性调节规律,但并未获得转模态控制规律的设计方法。Zheng等[8]建立了自适应循环发动机部件级性能计算模型,并分析了变几何参数对不同模态下发动机性能的影响。刘佳鑫等[9]用数值模拟方法研究了模态转换动态过程中流场参数的变化规律。张晓博等[10]分析了FLADE(Fan on Blade,叶片上的风扇)变循环发动机的模态转换过渡态特性,研究了几何参数调节及其不同组合形式对FLADE变循环发动机模态转换过程的影响。薛益春[11]和徐佩佩[12]对变循环发动机转模态过程的动态性能进行了模拟,但计算结果均出现了不同程度的超温、超转以及喘振裕度的波动。Ulizar和Pilidis[13]研究了可选择放气VCE模态转换过程的控制规律和特性。谢振伟等[14]针对变循环发动机提出了一种完全分布式控制框架,设计了分散控制算法和总线通信方案,并通过Simulink仿真验证了其适应性和鲁棒性。Corbett和Wolff[15]利用推进系统数值仿真(Numerical Propulsion System Simulation, NPSS)研究了转子动力学、雷诺数、空气湿度、部件热存储和燃油滞后对VCE过渡态性能的影响。Connolly等[16]建立了涵盖进气道、尾喷管和变循环发动机在内的准一维推进系统动态模拟模型,研究了整个推进系统的推力动态性能。笔者团队[17-18]研究了变几何参数对VCE过渡态性能的影响,提出了VCE过渡态控制规律设计的过渡态逆算法,通过7个步骤实现了典型工况下转模态控制规律的正向设计。宋可染等[19]提出了涡轮发动机过渡态性能计算的显式格式与隐式格式计算方法,通过直接给定过渡态过程中的涡轮前温度、共同工作点、燃烧室油气比或加速率实现发动机过渡态过程的模拟与最优控制规律设计。
综上所述,目前对VCE过渡态的研究主要集中在转模态过程性能的模拟,并研究影响VCE转模态性能的关键参数,或在某个特定的工况下试凑出一个基本可行的调节规律,无法避免发动机过渡态过程中超温、超转、喘振和贫富油熄火等现象。笔者[18]提出的基于纯功率提取法的转模态逆算法虽然实现了转模态控制规律的正向设计,但是步骤繁琐,且由于该方法是基于发动机稳态模型的,容积效应和转差等过渡态因素会带来微小的误差。
本文拟结合过渡态性能隐式格式计算方法[19]和VCE稳态逆算法[20-21]的建模思路,提出VCE过渡态性能直接模拟方法,并利用该方法改进VCE转模态控制规律设计流程,完成典型工况的转模态控制规律设计。
1 模型的建立
本文的研究对象为带CDFS双外涵变循环发动机(CDFS VCE),其基本构型和变几何部件如图1所示。这些变几何参数包括:风扇、CDFS和压气机的导叶角度αf、αCDFS和αc,模态转换阀(MSV)面积AMSV,前可变面积引射器(FVABI)面积A231,后可变面积涵道引射器RVABI面积A25,高/低压涡轮导向器喉部面积Anb,h和Anb,l,尾喷管喉部面积A8。
本文对变循环发动机的关键截面编号及定义如表1所示。

图1 CDFS VCE变几何部件示意图Fig.1 Schematic of variable geometries in CDFS VCE

表1 CDFS VCE关键截面编号及定义Table 1 Station numbers and their definitions of CDFS VCE
本章以该CDFS VCE为对象简要介绍稳态逆算法、隐式格式计算方法并在此基础上建立VCE过渡态直接模拟方法。
1.1 稳态逆算法
发动机部件级性能计算模型本质上是构建并求解非线性方程组的过程。对VCE而言,其方程组的自变量X又可以分为两类,第1类是发动机的状态参数和部件参数:
X1=[nl,nh,βf,βCDFS,βc,T4,πt,h,πt,h]T
(1)
式中:nh和nl为高低压转子转速;βf、βCDFS和βc为压缩部件工作点;T4为燃烧室出口总温;πt,h和πt,l为高低压涡轮落压比。
第2类参数为发动机的可变几何参数,如关键截面面积和压气机导叶角度等:
X2=[αf,αCDFS,αc,Anb,h,Anb,l,A8,A25,…]T
(2)
逆算法的思路是将X1作为已知量,而X2则为方程组的自变量通过非设计点迭代求解。通过上述措施,使得逆算法在计算前已经规定了发动机共同工作点等状态参数,确保了VCE工作在合理的区域,从而提高了模型的收敛性,消除了无意义的解。
文献[21]针对CDFS VCE双外涵模态建立的稳态逆算法模型如表2中模型1~5所示。特别地,考虑到Anb,h调节在工程上实现难度较大,部分VCE通常不对其进行调节,此时可仍将Anb,h作为给定参数,而βc则作为自变量,见模型6。表中被控参数为计算时的输入参数,而自变量则与残差方程共同组成非线性方程组。表2中6种逆算法的残差方程相同,均为Y=[δWg,4, δWg,5, δLh, δLl, δps,25, δWa,232, δWg,8]。其中δWg,4和δWg,5为高低压涡轮处的流量平衡;δLh和δLl为高低压转子的功平衡;δps,25为混合器处两股气流的静压平衡;δWa,232为FVABI处的流量平衡;δWg,8为尾喷管喉部流量平衡。单外涵模式下残差方程δWa,232替换为风扇出口与CDFS进口的流量平衡δWa,21,其他不变。

表2 CDFS VCE的稳态逆算法模型Table 2 Reverse method modeling of CDFS VCE
1.2 隐式格式计算方法
隐式格式计算方法是针对定几何涡轮发动机提出的一种过渡态性能模拟与控制规律设计方法。该方法在发动机稳态部件级性能计算模型的基础上添加容积效应、转子加速功率等过渡态效应计算模型,从而获得发动机过渡态性能模拟模型。
发动机过渡态转子加速功率Pacc可描述为
Pacc=f(n,dn/dt)=
(3)
式中:Pacc为转子加速/减速功率,单位W;J为转子的转动惯量,单位kg·m2;n为物理转速,单位r/min;tk和tk+1代表相邻的2个时间节点,单位s。
本文采用激盘—容积模型计算容积效应,并采用式(3)计算转子动力学效应。这2个模型与文献[19]完全相同,不再赘述。由于Pacc是发动机转速和加速率的函数,同时,在容积效应计算模型中也考虑了温度、压力、流量等参数对时间的导数,因此发动机过渡态方程组是非线性微分方程组。
与常规过渡态模型不同的是该模型不是以燃烧室燃油流量Wfb(与燃烧室油气比FAR4等效)为输入,而是直接给定过渡态过程中nh、nl、T4、βc或βf的变化历程。从而使得发动机按照给定的热负荷限制、稳定性限制或加速率限制进行加减速。发动机过渡态性能模拟过程即为最优控制规律设计的过程,控制规律设计精度完全取决于过渡态模拟模型的精度,设计结果不存在理论误差。
文献[19]针对双轴分排带增压级的定几何涡扇发动机建立了隐式格式计算方法的模型,并且证明了该模型解的唯一性。本文进一步将该方法推广到CDFS VCE中,建立的隐式格式计算方法模型如表3所示。发动机类型的变化不会影响模型的适用性,故本文不再证明该模型解的唯一性。表中所有模型的残差方程相同,均为:Y=[δWg,4, δWg,5, δLh, δLl, δps25, δWa,232, δWg,8]。单外涵模式下残差方程δWa,232替换为δWa,21,其他不变。

表3 CDFS VCE过渡态隐式格式计算模型Table 3 Transition implicit model for CDFS VCE
计算时首先给定期望的状态参数(βc,βf,T4,nh,nl中的一个)随时间的变化历程,作为过渡态计算的输入条件。过渡态性能模拟为已知tk时刻发动机状态确定tk+1时刻发动机状态的过程。首先根据时间节点tk+1从状态参数变化历程中插值获得βc,βf,T4,nh,nl中的一个作为输入,代入过渡态隐式格式计算模型程序中完成tk+1时刻迭代计算,接着进入下一时间节点并重复上述计算工作,直至过渡态计算结束。计算中按照式(3)计算tk+1时刻发动机转子的剩余功率并计入转子功率平衡方程。
隐式格式计算模型中默认变几何参数为定值或者按照已知的规律变化,因此该方法无法完成变几何参数调节规律的设计。
1.3 VCE过渡态直接模拟方法
变循环发动机过渡态性能模拟是指获得发动机性能参数、部件参数、气动热力参数随时间的变化历程。常见的过渡态性能模拟方法以变几何参数X2和燃油的变化历程作为性能模拟的输入,这些可调参数的变化历程即为VCE过渡态控制规律,而状态参数X1则为输出结果。在该框架下,过渡态性能模拟为动态泛函约束条件下的非线性微分方程组求解问题:
Y=F(t,X1)
subject to:H(X1)≥0
(4)
式中:Y=F(t,X1)为描述发动机过渡态整机匹配条件的非线性微分方程组。H(X1)为约束函数,具体表达式如下:

(5)
其中,h1(n,β)≥0为最小喘振裕度的约束,ΔSMmin为最小喘振裕度;h2(T4) ≥0为最高涡轮前温度的约束;h3(Wfb) ≥0为贫富油熄火边界的约束;z1(n,β)将压缩部件喘振裕度描述为转速n与β值的函数;z2(Wfb)则将燃烧室油气比FAR4描述为Wfb的函数。
X1可进一步描述为时间t和X2的函数,即X1=G(t,X2)。可见,H(G(t,X2))为动态泛函,H(X1) ≥0构成了方程组的约束条件。
式(4)中假设X2没有限制,考虑到VCE设计阶段需要给出变几何参数的调节需求,而部件往往难以给出变几何参数的限制,上述假设仍有现实意义。对给定的VCE进行仿真时则应考虑X2的限制。
模型的输入条件X2与约束条件H(G(t,X2)) ≥0之间的动态泛函关系增加了X2确定的难度,影响了常规过渡态模型的收敛性,增加了控制规律设计的难度,不可避免地出现了超转、超温或喘振的现象。
解决该问题的核心是对动态泛函约束进行简化。稳态逆算法和隐式格式计算方法为解决该问题提供了思路,即以变几何参数X2替换过渡态非线性方程组Y=F(t,X1)中的状态参数X1,使得X1成为模型的输入参数。在该框架下,过渡态性能模拟简化为简单约束条件下的非线性微分方程组求解问题:
Y=F1(t,X2)
subject to:H(X1)≥0
(6)
式中:Y=F1(t,X2)为以X2为自变量的非线性微分方程组。
由涡轮前温度、喘振裕度、油气比和加速率等的定义以及式(5)可知,根据约束H(X1) ≥0可直接确定出X1的取值范围,在该范围内给定X1的值,可直接通过式(7)完成发动机过渡态性能模拟,并保证满足过渡态的限制条件。正是因此,该方法被称为过渡态直接模拟方法。
Y=F1(t,X2)
(7)
基于表2中双外涵模态稳态逆算法模型建立的6种VCE双外涵过渡态直接模拟方法模型见表4。6种模型的给定参数、自变量和残差方程分别与表2中6种稳态逆算法一致。所不同的是直接模拟方法在每一个时间节点上均求解该模型,且部件气动热力计算时计入了容积效应的影响,而由式(3)计算的转子剩余功率也被计入功率平衡方程δLh和δLl中。
模型中风扇和压气机的导叶角度αf和αc按照各自的换算转速进行闭环控制,αf和αc对风扇和压气机特性的影响已经包含在所使用的风扇和

表4 CDFS VCE过渡态直接模拟方法模型
压气机特性中,故不再将αf和αc作为独立的变量进行研究。FVABI则按照CDFS的压比进行闭环控制,而MSV仅在模态转换过程中需要调节,因而αf、αc、A231和AMSV并未出现在整机模型中。
6种模型可分别对拥有不同变几何参数的VCE进行模拟。当只有A8可调时,可同时给定过渡态过程中的nh和nl;当A8和Anb,l可调时,可同时给定nh,nl和T4;以此类推,当A8,Anb,h,Anb,l,A25和αCDFS均可调时,可同时给定nh,nl,T4,βc,βf和βCDFS。当A8,Anb,l,A25和αCDFS可调,而Anb,h不可调时,可同时给定nh,nl,T4,βf和βCDFS。
模型给定参数中,nh和nl的变化历程即为发动机的加速率,T4表征发动机的热负荷,而βc、βf和βCDFS则确定了压缩部件的喘振裕度。模型中T4和FAR4完全等效,因而在需要限制燃烧室油气比的条件下,可将模型中的T4替换为FAR4,从而实现定油气比的算法。因此VCE的直接模拟方法可按照给定的加速率、热负荷限制、油气比限制以及喘振裕度限制模拟VCE的过渡态性能。上述特点使得采用该方法进行VCE过渡态性能模拟和控制规律设计将比采用常规的VCE过渡态性能模拟方法更为方便和准确。
6种模型的残差方程相同,均为Y=[δWg,4, δWg,5, δLh, δLl, δps,25, δWa,232, δWg,8]。对于CDFS VCE而言,其过渡态直接模拟方法模型为7元非线性方程组。单外涵过渡态直接模拟方法模型也与单外涵稳态逆算法模型的给定参数、自变量和残差方程相同,不再赘述。
计算时首先给定期望的状态参数(βc,βf,βCDFS,T4,nh,nl)随时间的变化历程,作为过渡态直接模拟方法的输入条件。具体的过渡态计算过程为已知tk时刻发动机状态,求tk+1时刻发动机状态的过程。根据时间节点tk+1从输入的状态参数变化历程中差值获得状态参数的输入值,按照式(3)计算tk+1时刻发动机转子的剩余功率并计入转子功率平衡方程,并将状态参数输入值代入到过渡态直接模拟程序中完成tk+1时刻迭代计算,获得tk+1时刻所需的变几何参数(A8,βc,Anb,l,A25,αCDFS等)、燃烧室供油量和转子加速率,接着进入下一时间节点并重复上述计算工作,直至过渡态计算结束。从输出的结果中提取出换算油气比或换算加速率,并采用合适的参数进行描述,即可获得VCE过渡态过程开环或闭环控制规律。
1.4 VCE过渡态直接模拟方法的验证
以某CDFS VCE的双外涵加速过程为例。原有的加速过程以供油量和几何调节规律作为过渡态计算的输入条件,采用常规的过渡态计算模型计算。获得原有的加速特性后,用nh,nl,T4,βc,βf的计算结果作为输入,分别按表3中的模型1、2、3和表4中的模型5和模型6来计算VCE的加速过程。直接模拟方法计算结果与常规模型的加速过程对比如图2所示。计算结果表明,表4中的模型5和模型6的计算结果完全一致,因此,模型6的计算结果不在图中展示。
模型1、2、3中分别给定nh,nl或T4,同时在这3种模型中所有变几何参数的调节规律均按照常规模型的计算结果给定。模型5中给定发动机6个状态参数nh,nl,T4,βc,βf,βCDFS随时间的变化规律,迭代求解变几何参数和燃油流量的调节规律。
可见常规模型与直接模拟方法计算结果中nl的最大误差为0.58%,nh的最大误差为0.35%,而T4和A8的模拟结果无显著误差。这些误差是由直接模拟方法中nh,nl,T4,βc,βf等输入参数插值带来的。证明适用于VCE的直接模拟方法模型正确,其计算精度与常规的过渡态计算模型基本一致。


图2 VCE过渡态直接模拟方法与常规方法的结果对比Fig.2 Simulation results of direct simulation method and conventional method
2 算例与分析
下面采用VCE过渡态直接模拟方法对文献[18]中提出的VCE转模态性能模拟和控制规律设计方法进行改进,以超声速巡航状态下单外涵转双外涵的模态转换过程为例,对转模态过程进行模拟和控制规律设计,并对2种方法的设计结果进行对比。
2.1 VCE转模态直接模拟方法
文献[18]中基于纯功率提取法提出了VCE的转模态逆算法,并通过7个步骤实现了典型工况下的VCE转模态控制规律设计和性能模拟,见图3左侧框图。该方法仍然存在2点不足:一方面,转模态逆算法中未考虑容积效应和转子转差等过渡态效应,使得控制规律设计存在一定的误差;另一方面,该方法流程复杂,操作困难。
针对上述不足,本文提出采用直接模拟方法实现VCE转模态性能模拟和控制规律设计。利用直接模拟方法设计VCE转模态控制规律的思路见图3右侧框图。该方法的步骤如下:

图3 两种转模态模拟方法流程对比Fig.3 Processes of two mode-transition simulation methods
第1步:由转模态前后发动机的工作状态结合稳态控制规律确定转模态起始点和终了点上的发动机状态参数X1=[nh,nl,βf,βCDFS,βc,T4],并分别标记为X1,initial和X1,final。
第2步:给定对X1随时间的变化规律并使得起始时刻和终了时刻的X1分别等于X1,initial和X1,final。
X1=F(time)
(8)
第3步:将X1的变化规律代入到基于直接模拟方法的转模态过渡态性能计算程序中直接计算获得变几何参数、燃油流量的变化规律以及发动机转模态过程中的性能。
第2步中,在给定转模态过程转速变化曲线时应避免曲线突然转折,亦即避免曲线不可导的情况,因为转速变化曲线的斜率代表了转子的加速率,而加速率的突变将导致变几何参数的突跃,这在工程上是不可实现的。
转模态过程中FVABI的调节规律与稳态条件下的调节规律不同:双外涵转单外涵时A231开度逐渐增加,增加第2涵道的背压,减少第2涵道的流量;反之,A231逐渐关小,减小第2涵道的背压,增加第2涵道的流量。转模态过程中MSV随着第2涵道流量的变化在最大开度与完全关闭2个状态之间快速切换,MSV在中间状态停留会带来突扩损失。AMSV的调节规律应与A231的调节规律相匹配,否则会导致第2涵道气流临界或者倒流。本文采取的方法是给定所期望的MaMSV变化规律,在转模态过程的动态计算中使用给定MaMSV求AMSV的算法即可求解获得AMSV的调节规律,从而有效避免由于AMSV给定不合适而引起的MSV截面临界或倒流的情况。
可见基于直接模拟方法的转模态控制规律设计方法只需要3步即可完成VCE转模态控制规律设计和转模态性能模拟,比基于纯功率提取法的转模态逆算法更为简便实用。
2.2 发动机主要设计参数
本文所研究的CDFS VCE采用高导喉部面积不可调的方案,其他变几何参数如图1所示。该VCE主要参数如表5和表6所示。表中H为飞行高度;Ma为飞行马赫数;Fn为非安装推力;Fs为单位推力;SFC为非安装耗油率;Wa为发动机进口空气流量;BPR为总涵道比;πf为风扇压比;πc为压气机压比;πCDFS为CDFS压比。
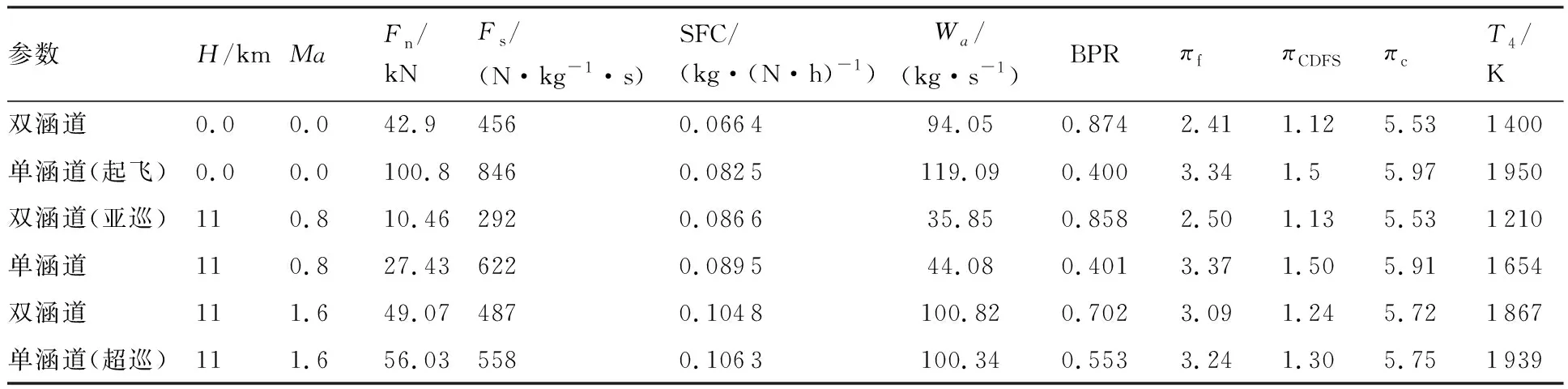
表5 CDFS VCE关键状态下的性能参数Table 5 Performance parameters of CDFS VCE in key state

表6 CDFS VCE关键状态下的变几何参数Table 6 Variable geometry parameters of CDFS VCE in key state
根据发动机尺寸重量评估的结果预估的发动机高低压转子的转动惯量分别为12.78 kg·m2和14.17 kg·m2。本文所采用的CDFS特性为GE公司于1979年公布的核心机驱动风扇的部件特性[22],并使用文献[18]介绍的变几何压缩部件特性三元插值方法进行插值。
2.3 超声速巡航单外涵转双外涵性能模拟
本节利用基于直接模拟方法的转模态控制规律设计方法完成CDFS VCE在超声速巡航状态下单外涵转双外涵的控制规律设计与性能模拟,并将模拟结果与文献[18]中基于纯功率提取法的转模态控制规律设计结果进行对比。本算例所研究的CDFS VCE高压涡轮导向器喉部面积不可调,在计算时使用了表4中的模型6。
发动机在超声速巡航状态下迅速节流,发动机流量减小,进气道背压升高,将导致进气道结尾正激波被推出唇口,进气道进入亚临界状态,从而引发进气道甚至是发动机的喘振。这一现象制约了发动机的过渡态响应速度。而VCE可保持发动机进口流量不变的情况下从单外涵模态转到双外涵模态,并在双外涵模态下进一步等流量节流,从而实现发动机推力的快速下降。
超声速巡航状态下单外涵最大状态与双外涵最大状态发动机的性能参数、循环参数和变几何参数见表5和表6。给定2种状态下发动机的状态参数[nh,nl,T4,βf,βCDFS]作为转模态过程的起始点和终了点,并给定转模态过程中状态参数的变化规律。采用直接模拟方法计算获得了转模态过程中变几何参数和燃油的控制规律,如图4所示。发动机主要状态参数、喘振裕度(ΔSM)和关键截面马赫数如图5所示。其中Ma22和Ma25分别代表MSV和RVABI出口的马赫数,Ma231和Ma232分别代表FVABI内外涵出口的马赫数。

图4 超巡状态单外涵转双外涵过程变几何参数变化规律Fig.4 Control schedule of variable geometry parameters during mode transition(Single-bypass mode to Dual-bypass mode at supersonic cruise)
在2.1节中已经说明,单外涵转双外涵时A231逐渐关小,而MSV则应在较短的时间内迅速打开。由图4可知,在转模态的起始阶段,对A231进行了预收,目的是减小第一外涵出口静压,避免MSV打开的瞬间第二外涵出现倒流,这也导致了其他参数的微小波动。在约0.1 s时,MSV的面积A22迅速打开到最大值,以保证Ma22按照给定的规律变化。
转模态前后A8放大了12.5%,以适应发动机压比的降低。Anb,l用以控制高低压转子转差以及高压转子转速变化率:在0.8 s以前,Anb,l关小约7%,以降低高压涡轮落压比,减小高压涡轮功,使得nh降低;在0.8 s以后,高压转子转速下降率减小,需要打开Anb,l约2%,以增加高压涡轮落压比和功。A25主要用于调节风扇和CDFS的喘振裕度以及涵道比,其变化趋势与Anb,l相反:在0.8 s以前,A25逐渐打开约106%,以适应涵道比的增加;在0.8 s以后,A25减小约12.5%。

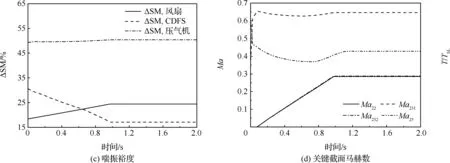
图5 超巡状态单外涵转双外涵过程主要参数变化历程Fig.5 Parameters during mode transition(Single-bypass mode to Dual-bypass mode at supersonic cruise)
CDFS导叶角度主要用于调节CDFS的压比、流量和喘振裕度,从单外涵到双外涵时πCDFS降低,CDFS导叶角度关小约35°。由于核心机转速下降且进口总压降低,使得核心机流量减少,主燃烧室燃油流量减少约14%。
由图5可见,转模态时间约为1 s,转模态过程中推力系数(T/TSL)下降14%,核心机转速下降1%,涡轮前温度下降3.7%,未出现喘振和截面临界的情况。且风扇转速保持不变,可实现等流量条件下的节流,从而避免进气道进入亚临界状态引发的喘振。需要说明的是,在高转速下,风扇的流量-压比特性比较陡,因此,在风扇转速和流量不变的情况下,压比降低,喘振裕度增加。
上述算例中所设计的变几何参数和燃油的控制规律并非最优,但是直接模拟方法为VCE过渡态控制规律的优化设计提供了有效的工具。
文献[18]中采用基于纯功率提取法的过渡态逆算法实现了超声速巡航状态下单外涵转双外涵过程的控制规律设计和性能模拟。本文以文献[18] 中给定的状态参数变化规律作为输入采用直接模拟方法实现了转模态过程性能模拟。图6对比了2种方法的模拟结果。可见纯功率提取法模拟结果中,转速、T4和喘振裕度的最大误差分别为0.04%、0.1%和1%。采用直接模拟方法的模拟结果保证了转速、涡轮前温度和喘振裕度严格按照给定的规律变化,提高了转模态过程控制规律设计与性能模拟的精度。

图6 两种设计方法模拟结果对比Fig.6 Simulation results of two methods
2.4 海平面静止双外涵转单外涵性能模拟
本节利用基于直接模拟方法的转模态控制规律设计方法完成CDFS VCE在海平面静止状态下双外涵转单外涵的控制规律设计与性能模拟。海平面静止状态下双外涵节流状态与单外涵最大状态发动机的性能参数、循环参数和变几何参数见表5和表6。给定2种状态下发动机的状态参数[nh,nl,T4,βf,βCDFS]作为转模态过程的起始点和终了点,并给定转模态过程中状态参数的变化规律,采用直接求解算法模型6计算了转模态过程中变几何参数的变化规律,如图7所示。发动机主要状态参数、喘振裕度和关键截面马赫数如图8所示。
在2.2节中已经说明,在给定转模态过程中转速变化曲线时应避免不可导的情况,从而防止变几何参数的突跃。为进一步证明该结论,在本算例中转模态起始阶段,高低压转子转速按照线性增加(见图8(a)),这就使得转模态其实时刻高低压转子的加速率出现了突升。这只能通过增加燃油流量或者改变发动机的几何来获得。在本文提出的方法中燃油流量的变化主要由T4的变化规律决定。在T4也按照线性变化的情况下(见图8(b)),只能通过变几何参数的调节来实现。结果是,转模态起始时刻A8和Anb,l分别阶跃了13%和8.6%,而A25也突降了约20%,见图7。这样的调节规律在工程上是无法实现的,可通过对转模态起始阶段的转速变化曲线进行光滑处理得到解决。
整个转模态过程中αCDFS、A231单调增加,该措施可降低双外涵模态下第2涵道的流量,为关闭MSV创造条件。转模态前后αCDFS从-58°增加至0°,而A231则从0.004 m2增加到0.04 m2。同时,Wfb则从0.8 kg/s增加到2.31 kg/s,以实现发动机的加速和推力提升。
在整个转模态过程中Anb,l均大于其目标值,这是为了增加高压涡轮落压比和功,以维持高压转子的加速率。在转模态的末期,高压转子加速率减小,Anb,l也逐渐减小到期稳态目标值。
在起始点之后A8逐渐关小,以提高风扇压比,增加单位推力和总推力,转模态前后A8收小了约30%。转模态过程中A25总体呈现缓慢增加的趋势,但是在MSV关闭的瞬间,由于外涵流量突然减小,使得A25产生了一定的波动,这表明当前给定的MSV关闭时机并非最佳。在双外涵转单外涵的过程中应该先通过增加CDFS转速和导叶角度并放大A231等措施减小第2涵道的流量直至接近0,此时迅速关闭MSV可避免A25波动。转模态前后A25增加了约25%。
图8表明,转模态时间为3 s,涡轮前温度从1 400 K增加至1 950 K,推力系数T/TSL从0.2增加至0.6,转模态过程中推力、转速、涡轮前温度实现了平稳过渡,未出现喘振和截面临界的情况。

图7 海平面静止双外涵转单外涵过程变几何参数变化规律Fig.7 Control schedule of variable geometry parameters during mode transition(Dual-bypass mode to Single-bypass mode at sea level)
上述算例表明,直接计算模型可以用于CDFS VCE转模态性能模拟和控制规律设计,与基于纯功率提取法的转模态控制规律设计方法相比,该方法更为简洁,且计算精度更高。
3 结 论
1) 定几何涡扇发动机过渡态隐式格式计算方法可推广到CDFS VCE中,在给定所有变几何参数调节规律和一个状态参数(nh,nl,T4,βc,βf,βCDFS)之一的条件下,其计算结果与常规的给定燃油的过渡态模拟模型计算结果误差不大于0.58%。
2) 将隐式格式计算方法与稳态逆算法相结合,可获得CDFS VCE过渡态性能直接模拟方法,该方法直接给定过渡态过程中nh,nl,T4,βc,βf,βCDFS中全部或部分参数的变化历程,直接计算获得所需的变几何参数与燃油流量的调节规律,计算结果表明直接模拟方法的计算精度与常规的CDFS VCE过渡态性能计算结果一致。
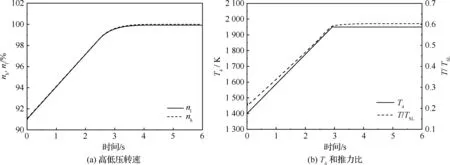
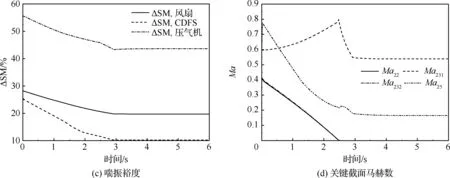
图8 海平面静止双外涵转单外涵过程主要参数变化历程Fig.8 Parameters during mode transition(Dual-bypass mode to Single-bypass mode at sea level)
3) 过渡态性能直接模拟方法可用于VCE转模态过渡态性能模拟和变几何参数控制规律的设计,与基于纯功率提取法的转模态控制规律设计方法相比,该方法可提高设计精度,简化设计流程。
4) 本文所研究的CDFS VCE在超声速巡航状态下,由单外涵模态转换为双外涵模态的时间不超过1 s,模态转换前后风扇流量保持不变,核心机转速下降1%、涡轮前温度下降3.7%,推力下降14%。
