空天飞行器整体式救生座舱的稳定减速与分离特性数值模拟

刘愿，陈川，钱战森,*

1. 中国航空工业空气动力研究院，沈阳 110034 2. 高速高雷诺数气动力航空科技重点实验室，沈阳 110034 3. 航空工业成都飞机设计研究所，成都 510100

空天飞行器是一种可重复利用、水平起降、高马赫数巡航、进入地球轨道的飞行器，因其具有高空侦察、快速突防及远程运输等特点而成为世界各国的研究热点。救生系统作为飞行器的关键部件之一，是飞行员空中的“生命之舟”，其安全分离和稳定减速等性能必须得以保证。尤其对于空天飞行器，救生系统必须能够在包含亚声速、超声速及高超声速等的宽速度范围内正常工作，才能保障飞行员在整个飞行包线内的生命安全。但是，常规弹射座椅救生包线一般高度为0～20 km，Ma<2[1]，无法满足该飞行包线内的救生要求。整体式密闭救生座舱方案将整个驾驶舱与座椅进行一体化设计，在弹射之后具有独立的密闭式结构，可在高马赫数飞行情况下有效保护飞行员免受高速气流的吹袭，能够大幅扩宽飞行器的救生包线，是空天飞行器救生系统设计的重要方案之一。

常规飞行器救生系统的研制主要以弹射座椅为主，先后经历了弹道式弹射、火箭弹射、多态控制弹射以及自适应弹射4个阶段的发展[1-2]。现阶段，各国作战飞机装配的弹射座椅(如美国ACES-II型弹射座椅、英国马丁贝克公司MK-16座椅及俄罗斯K-36型座椅)均属于第3代多态控制弹射座椅，第4代自适应座椅由于推力矢量技术瓶颈难以突破而尚未实现工程化应用，仍处于技术发展阶段。针对弹射座椅的气动问题，国际上已形成了以综合风洞试验、数值计算及数学建模等为手段的研究体系[3-7]。中国针对弹射座椅的出舱过程、姿态稳定与控制、飞行员保护措施等方面也开展了相应的研究工作，发展了弹射座舱气动性能预测的数值模拟方法[8-10]与风洞试验方法[11-12]、座椅增稳方法[13-17]、座椅姿态控制方法[18-19]、高速气流吹袭保护措施[20-21]等多项关键技术。但是，随着飞行器飞行马赫数的不断提高，常规弹射座椅救生方式已经难以完成高马赫数情况下的救生任务。

整体式救生座舱设计思想最初来源于空间运载器的返回舱以及B-58的密闭式救生座椅[22]，并在F-111飞机上获得了工程应用[23-24]，最大限度地保护了飞行员。但是由于该系统集成复杂、质量大且姿态难控制等诸多问题[25]，导致在F-111飞机退役后整体式座舱救生方式在其他型号上并未得到采用。现阶段常规战斗机仍主要偏向于配备飞行员简易保护装置的座椅救生方案，这使得针对整体式救生舱系统，尤其是对整体式座舱分离安全性、减速效率及姿态稳定等气动性能的研究较为少见，且所有研究针对的速度上限基本均在低超声速范围。对于宽速域飞行的空天飞行器，由于马赫数范围明显拓宽，整体式座舱所面临的各种问题将更加复杂。但是，近年来随着新型材料和控制系统的发展与应用，各系统集成、减重等问题有望逐渐获得突破，整体式座舱将成为新型空天飞行器的一种理想救生系统。然而目前国内外对于宽马赫数范围的整体式座舱稳定性和分离安全性等关键气动特性的研究仍十分缺乏。

本文主要围绕整体式座舱系统的气动稳定性和分离特性开展数值模拟研究。首先开展基本气动性能数值模拟，重点考察座舱在宽速域下的稳定性和减速效率；然后通过一种刚性减速伞减速增稳方案，对座舱稳定性和减速效率进行改善；最后基于动态重叠网格方法，对座舱+减速伞构型离机过程开展动态数值模拟，进一步验证座舱抛投的安全性、稳定性等性能。该项研究工作对开展空天飞行器救生系统设计具有一定的参考意义。

1 整体式救生座舱简介

整体式救生座舱方案将飞行员、任务系统、环境控制与生命保障系统等相关系统集成为一体，形成独立的结构，实现所谓的“短袖座舱”；应急救生促发后，座舱在分离机构的作用下与空天飞行器切断连接并弹射离体；在安全分离之后，通过稳定系统和降落伞实现安全着陆。整个弹射过程飞行员不会暴露于外界环境中，能够获得最好的保护，所以整体式座舱将成为一种较为理想的空天飞行器救生系统。

1.1 整体式救生座舱的气动构型

为更好地保护飞行员的生命安全，整体式座舱必须能够容纳飞行员、座椅、控制操纵平台和供氧装置等系统，并形成密闭式空间。同时整体式座舱作为空天飞行器机体的一部分，其外部型面还应与飞机进行一体化设计。研究的整体式救生座舱如图1所示，座舱上表面为飞行器舱盖，在正常飞行时其他表面均位于机体内部，其空间能够容纳驾驶舱，紧急抛投指令触发后座舱整体弹出。

整体式救生座舱模型具体尺寸如图2所示，模型总长为4.46 m，宽1.10 m，高1.43 m，重心位置距离座舱前缘点1.98 m，距离座舱下端面0.77 m。 座舱总质量m=900 kg，转动惯量IXX=169.123 kg·m2、IYY=805.263 kg·m2、IZZ=727.988 kg·m2。

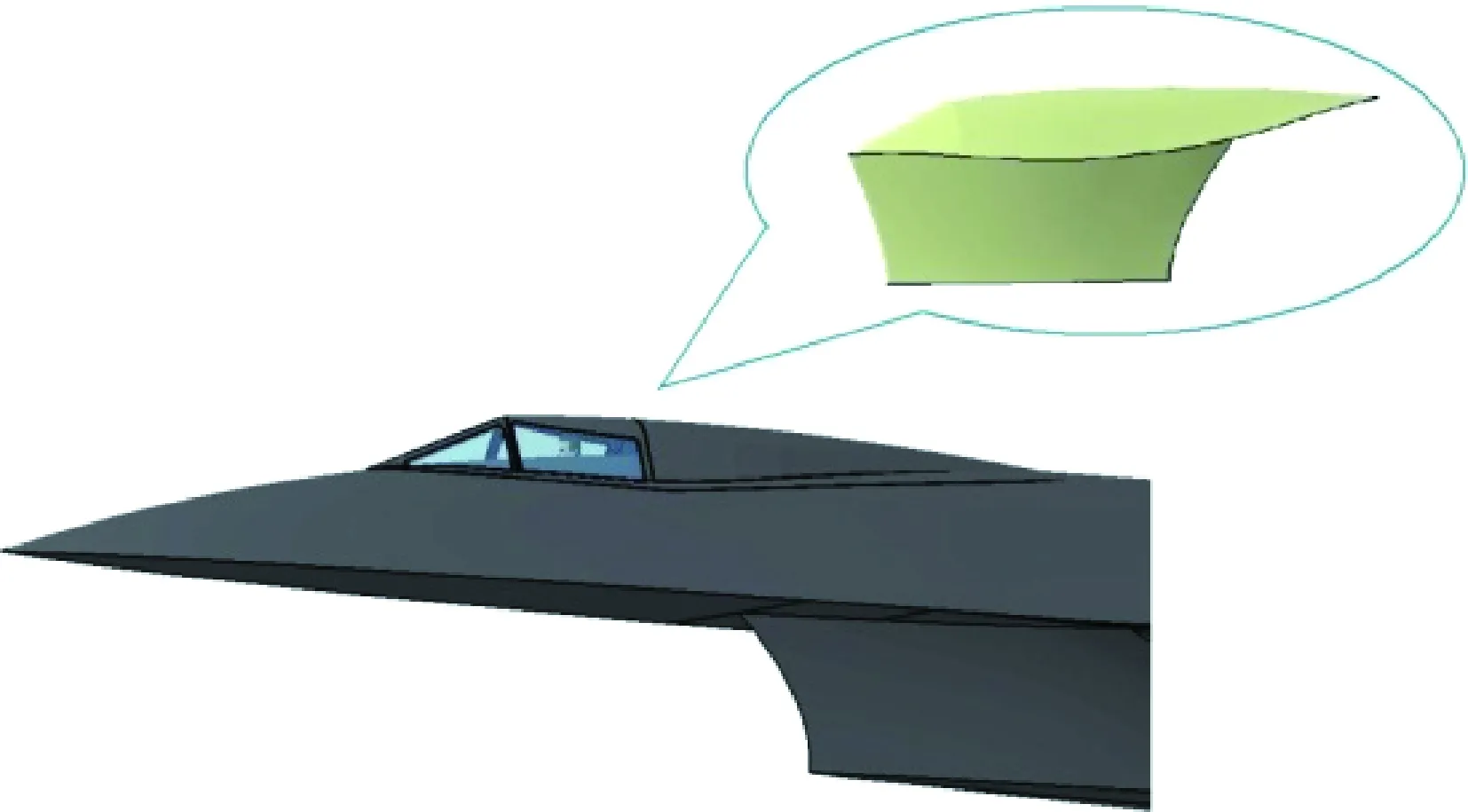
图1 整体式救生座舱示意图Fig.1 Concept configuration of integral escape module

图2 整体式救生座舱总体尺寸Fig.2 Overall sizing for integral escape module

1.2 整体式救生座舱的工作模式

为保证座舱与机体的安全分离，并满足飞行员的身体耐受范围，在座舱弹射初期采用轨道弹射和火箭助推的方式，使座舱获得足够的离机法向高度，同时控制座舱加速度小于人体承受极限。根据轨道弹射和火箭助推的作用时间范围，整体式座舱弹射过程可分为滑道弹射、火箭助推以及自由飞行3个阶段，各个阶段的主要参数如表1所示。

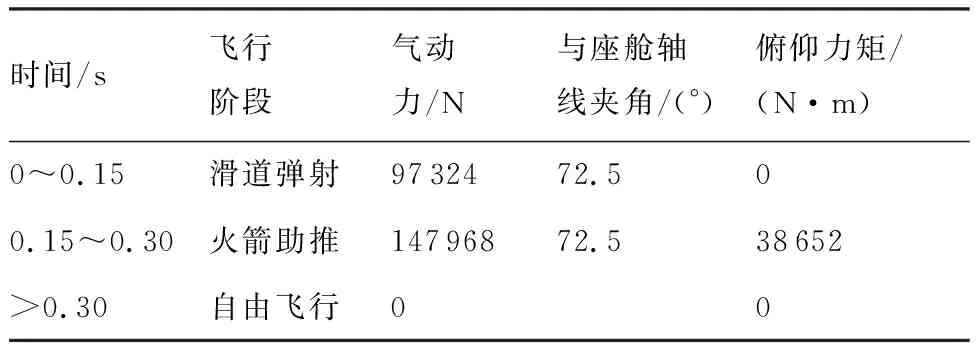
表1 整体式救生座舱抛投过程Table 1 Ejection process of integral escape module

针对上述座舱构型，首先采用数值模拟方法开展基本气动性能计算，并重点评估整体式座舱在宽速域下的稳定性和阻力特性；之后基于该构型，开展整体救生系统增稳减速方案的设计与评估。

2 数值模拟方法

数值模拟采用ARI-OVERSET软件，该软件是中国航空工业空气动力研究院的自研数值模拟平台[26]。该平台能够高效地完成航空领域的多种工程计算任务，并广泛应用于飞行器设计。重叠网格方法作为该平台的关键技术之一，在武器投放、变几何进/排气系统等诸多多体相对运动的动态数值模拟中获得了可信的计算结果[27-29]。

2.1 重叠网格方法

重叠网格方法[30]最初用于降低复杂构型的网格划分难度，后来被广泛运用于多体相对运动问题的数值模拟。对于多体相对运动的数值模拟，每一时刻物体间的相对位置均发生变化，网格应与物体随动，实时更新，传统多块拼接和变形网格技术在处理该类问题时将遇到困难。重叠网格方法将各个物体各自划分网格，通过挖洞和插值将各套网格联系在一起。如图3所示，计算网格分为两个部分：背景网格和包含圆形物面的子网格，在数值模拟过程中，子网格外边界被定义为挖洞边界，位于该边界内的背景网格单元被挖掉，并形成背景网格的内边界；背景网格内边界和子网格外边界的流场数值将通过附近对方网格的数据插值获得，从而完成两套网格之间的数据传递。当网格随物体运动而更新时，包含运动边界的网格块跟随物体运动，但网格质量和拓扑结构均不会发生改变，故重叠网格方法在多体运动应用方面具有较高的灵活度、较广的适应性以及较强的鲁棒性。

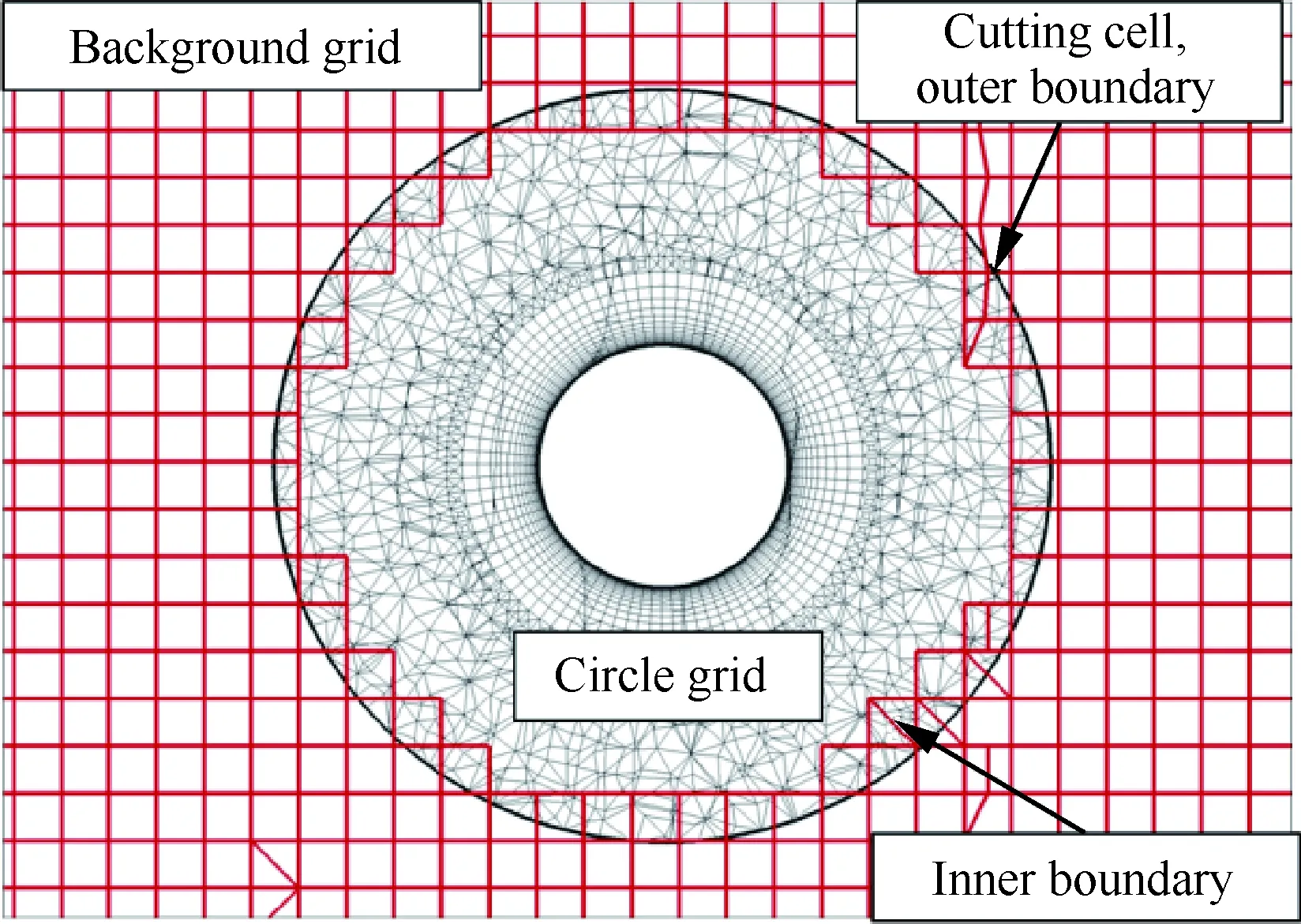
图3 重叠网格示意图Fig.3 Sketch map of chimera grid technique

2.2 数值求解格式

Navier-Stokes(N-S)方程的无黏项采用二阶精度Roe格式离散，黏性项采用二阶中心差分格式离散，并采用Spalart-Allmaras(S-A)单方程湍流模型；非定常计算时，时间推进采用二阶精度双时间步迭代方法，物理时间步采用二阶向后差分格式，内迭代采用一阶隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)格式。救生座舱物面采用无滑移边界条件，远场边界采用黎曼无反射条件。研究的来流速度范围为Ma=0.3～4.0，飞行高度范围为H=0～30 km，沿飞行包线的具体参数见表2。

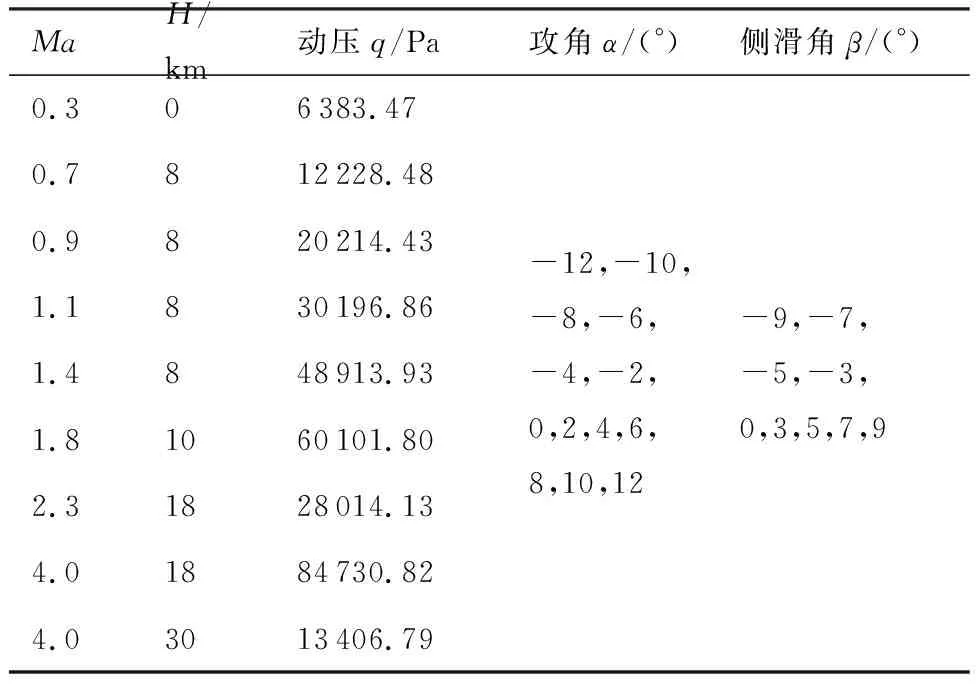
表2 数值计算工况Table 2 Numerical simulation conditions

2.3 计算网格

整体式座舱气动性能计算采用内外层相结合的结构/非结构混合网格，物面网格为结构网格形式，在靠近物面的区域采用长宽比较大的棱柱体网格识别边界层流动，在远离物面的区域采用四面体网格填充，如图4所示。这种处理方式可在满足精度要求的前提下大幅减小网格总量，提高计算效率。物面第1层网格高度保证y+<10，并针对模型前后缘和物面曲率变化较大的区域进行网格加密。

采用的重叠网格技术、计算方法以及网格划分策略等数值模拟方法的可靠性在多个典型算例中已得到了验证：在NACA0012翼型强迫振荡算例中气动载荷迟滞曲线与实验结果一致[27]；在涡轮基组合发动机(Turbo-Based Combined Cycle，TBCC)进气道模态转换气动性能计算中，进气道沿程压力分布与实验结果良好吻合[28]；在美国空军机翼/挂架/外挂弹组合体的典型投放验证算例

图4 整体式救生座舱网格示意图Fig.4 Grid illustration of integral escape module

计算中，外挂物重心位置、姿态角等轨迹特性均与实验数据一致[29]。故不再给出数值模拟方法验证的细节。

3 整体式救生座舱静态气动特性分析

为获得整体式救生座舱在宽速域范围内的气动特性，采用ARI-OVERSET对其开展数值模拟计算，计算工况如表2所示，包含了亚声速、跨声速及超声速等宽速域范围。

图5给出了抛投包线内典型马赫数情况下的流场马赫数云图。在亚声速(Ma=0.7)情况下，流动首先经过座舱前体时受到压缩而加速，但因来流速度较低，在型面拐角处也未能形成声速，随

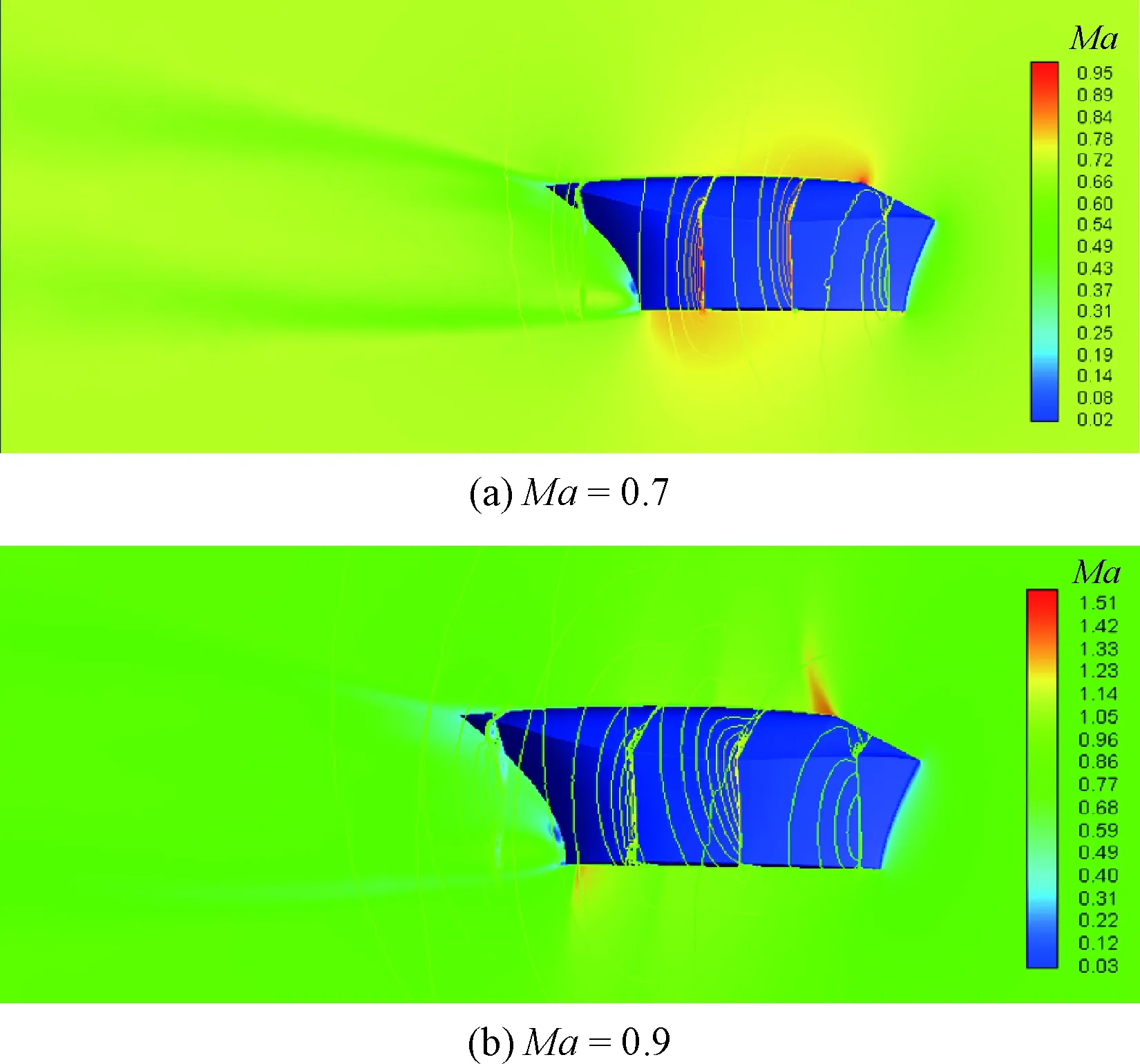
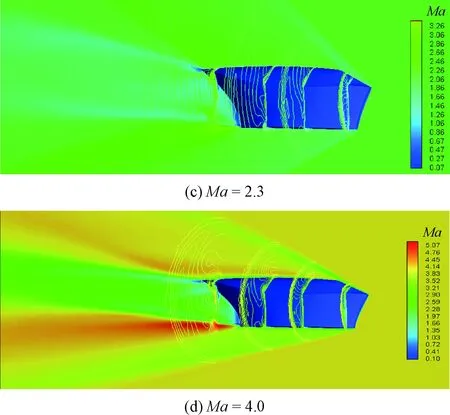
图5 α=6°、β=0°时典型马赫数情况下整体式救生座舱马赫数云图Fig.5 Mach contour of integral escape module for typical Mach numbers at α=6°, β=0°

后在膨胀的后体型面作用下减速，最后在座舱后缘形成尾迹区；在跨声速(Ma=0.9)情况下，流动在前体的压缩作用下速度快速升高，并在型面拐角附近达到声速，且在来流攻角为6°的情况下，座舱上表面结尾激波前移，接近型面拐角，而下表面型面为平面，结尾激波处于后缘；在超声速情况下，首先来流在座舱前体形成前缘斜激波，且随马赫数的增加，激波强度增加，激波面更靠近物面，但波后马赫数仍为超声速，之后在后体收缩型面的作用下速度有所回升，最后在后缘形成结尾激波以及尾迹区。

可见在宽速域情况下，整体式座舱绕流流场结构随着来流马赫数的变化而发生明显改变，进而将影响整体式座舱的气动特性。图6给出了Ma=0.3～4.0时整体式座舱的纵向气动特性曲线。可见在亚声速情况下，气动特性系数(升力系数CL和俯仰力矩系数Cmy)斜率随马赫数的增加而增加，如图6(a)～图6(c)所示，而超声速条件下其随马赫数的增加而减小。升力系数在整个弹射包线内随攻角增加呈近似线性增长；阻力系数在负攻角情况下变化较大，而在正攻角情况下变化平缓，并随马赫数的增加而增大，亚声速情况下的阻力远低于超声速情况。俯仰力矩系数Cmy在攻角-12°～12°范围内虽未呈现出线性分布规律(如图6(c)所示)，但从曲线变化趋势可以看出大部分工况下整体式救生座舱处于纵向静不稳定状态(Cmy曲线斜率大于0)，且在正攻角情况下尤为严重。

为更为准确地评估整体式救生座舱各个工况下的纵向静稳定性，采用中心差分离散方法，求解每个攻角下的∂Cmy/∂α，结果如图6(d)所示，可见大部分工况下整体式救生座舱处于纵向静不稳定区域(∂Cmy/∂α>0)，且随着马赫数、攻角的增加，处于不稳定区域的范围也逐渐增加。

图7给出了Ma=0.3～4.0时整体式座舱的横、航向气动特性曲线。在-9°～9°的飞行侧滑角范围内，整体式救生座舱横向力系数CY、偏航力矩系数Cmz以及滚转力矩系数Cmx呈近似线性分布，如图7(a)～图7(c)所示，且侧力和偏航力矩随着侧滑角的增加而降低，而滚转力矩升高。采用最小二乘法对各曲线进行线性拟合，获得整体式座舱在Ma=0.3～4.0范围内的∂Cmx/∂β和∂Cmz/∂β，如图7(d)所示。根据静稳定性的判断准则，整体式座舱在整个弹射包线内，横、航向均呈静不稳定性(∂Cmx/∂β>0、∂Cmz/∂β<0)。

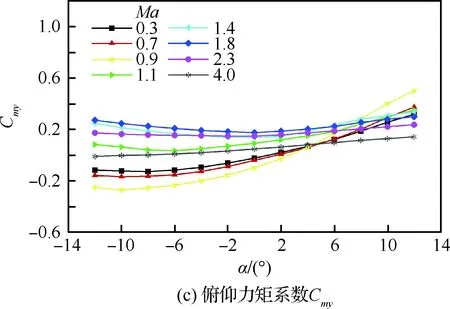
图6 整体式救生座舱宽速域纵向气动特性曲线Fig.6 Longitudinal aerodynamic coefficients of integral escape module for wide Mach number range

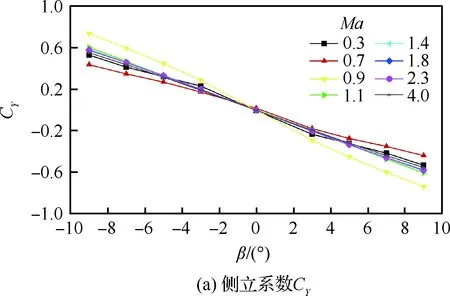
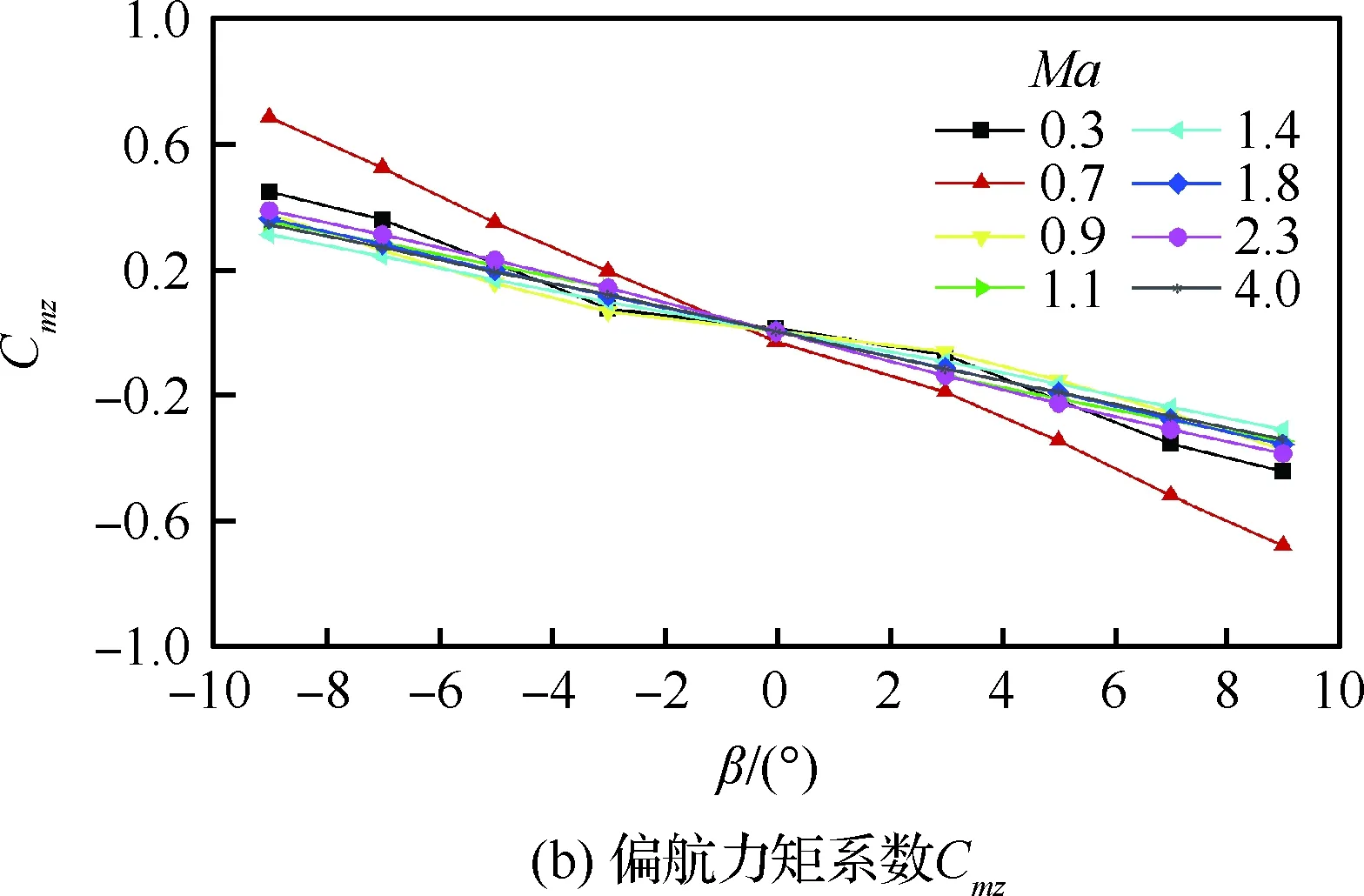
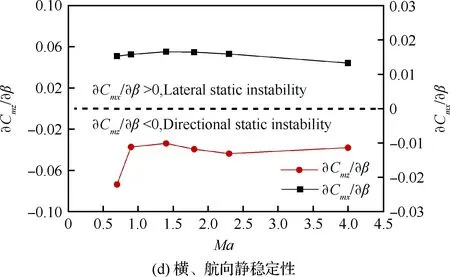
图7 整体式救生座舱宽速域横、航向气动特性曲线Fig.7 Lateral and directional aerodynamic coefficients of integral escape module for wide Mach number range

因此，1.1节给出的整体式救生座舱构型虽然能够较好地保护飞行员不受气流吹袭，但因其特殊的气动外型而存在严重的不稳定性问题，无法保障飞行员的过载范围。

4 刚性减速伞增稳方案及评估

第3节研究表明，整体式座舱在宽速域范围内稳定性并不理想，而整体式座舱又无法配置可调节力矩特性的主动姿态控制机构(如舵面等)，这将导致座舱在抛投过程中容易出现姿态发散而失控，严重影响飞行员的生命安全，因此，设计一种实用且结构易实现的增稳方案尤为重要。目前弹射救生系统的稳定减速方案主要有3种：柔式稳定装置、微调火箭稳定装置及硬式稳定装置[31]。柔式稳定装置即柔性稳定伞在强烈气动力/热载荷作用下将遭到严重破坏而在高马赫数情况下无法正常工作；微调火箭稳定装置虽能在高速弹射时大幅提升座椅的稳定性，但因推力矢量、智能化控制等关键技术的限制而尚处于验证阶段；硬式稳定装置通过改变座椅的气动外形改善气动特性，在高马赫数情况下可有效改善座椅的稳定性，其结构形式主要包括稳定板和伸出式刚性减速伞。稳定板因距离座椅重心较近且气动载荷较小，对座椅稳定性的改善能力比较有限；而刚性减速伞借助可伸缩式套筒远离座椅重心，能够更为高效地改善座椅的气动特性。本文将尝试采用刚性减速伞方案，在分离前将减速伞安置于座舱内部，分离后借助多级伸缩杆快速顶出，通过减速伞带来的气动载荷增量提高座舱的气动性能。第4节将针对该减速伞方案分别开展静、动态数值计算，评估其对座舱的增稳特性以及减速效率。

4.1 刚性减速伞增稳方案

减速伞具体尺寸如图9所示，减速伞由球面和锥面组成，球面半径为0.60 m，锥面半锥角为69°；两个减速伞对称分布在座舱左右两侧，通过三级伸缩式稳定杆与座舱连接，与座舱纵向中心面成9°夹角，并垂直于座舱轴线，且与座舱前端点距离1.84 m。为考虑座舱整体质量的分布且进一步提高稳定性，将座舱重心偏移到距离前缘端点1.48 m的位置。

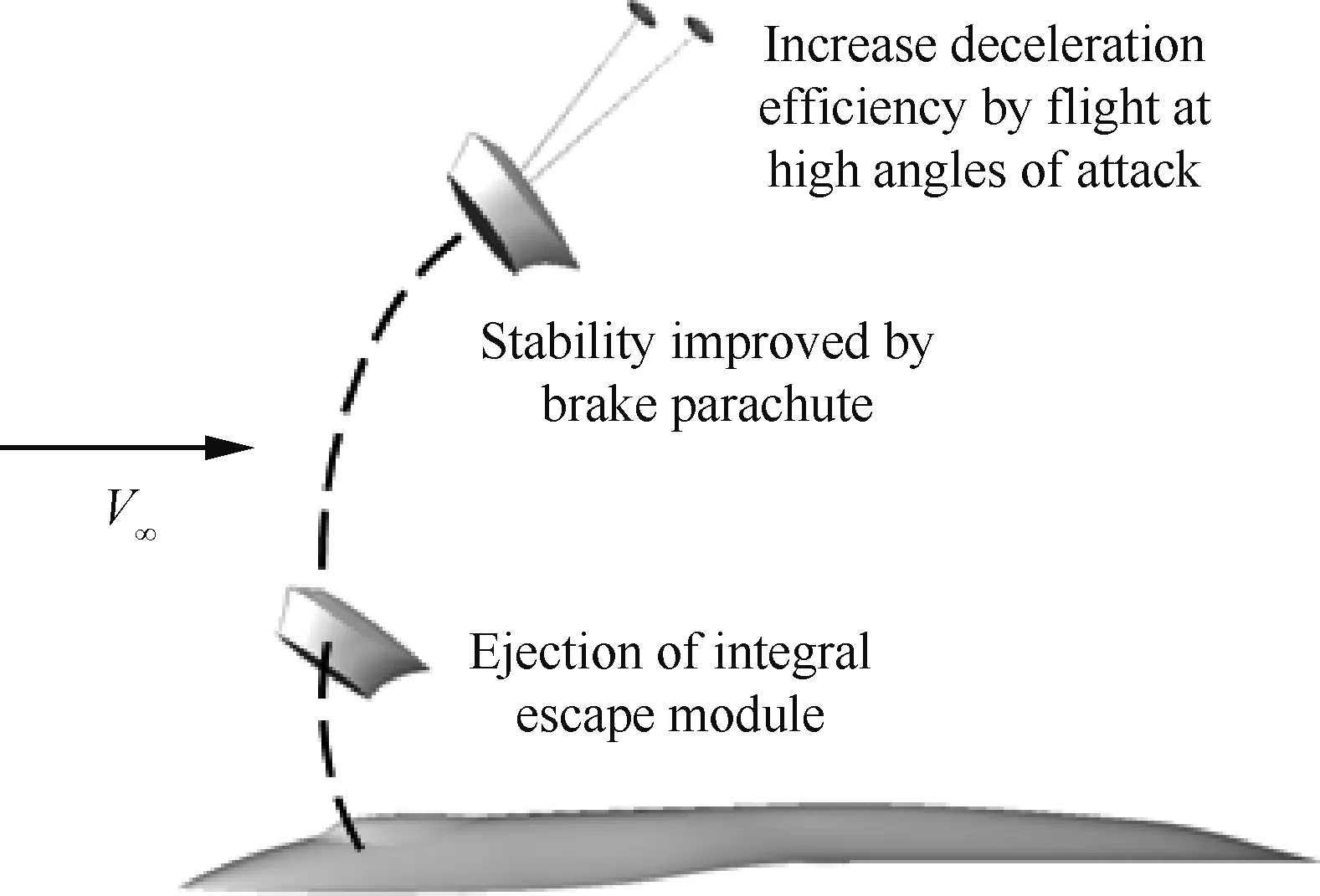
图8 整体式救生座舱抛投轨迹示意图Fig.8 Illustration of separation trajectory of integral escape module

图9 减速伞尺寸示意图Fig.9 Size illustration of brake parachute

4.2 静稳定性评估

计算网格如图10所示，同样采用内外层结合的结构/非结构混合网格，物面第1层网格高度保证y+<10，针对模型前后缘以及物面曲率变化较大的区域进行网格加密。考虑该座舱系统将以大攻角状态自由飞行，将气动评估攻角序列更改为α=30°～70°、Δα=5°，侧滑角序列更改为β=-20°～20°、Δβ=5°。

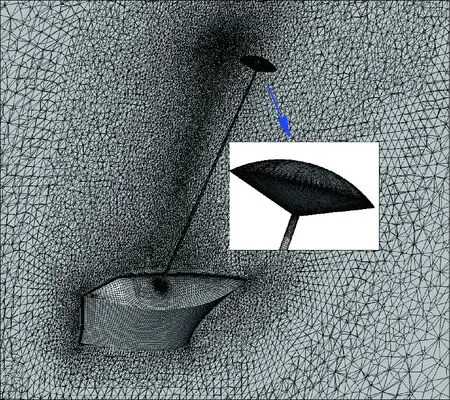
图10 整体式座舱+减速伞构型计算网格示意图Fig.10 Grid illustration of integral escape module with brake parachute

图11给出了抛投包线内典型马赫数情况下的流场马赫数云图。在亚声速(Ma=0.7)情况下，流动经过整体式座舱前体时受到压缩而加速，并在上表面前缘形成小范围的超声速流动，同时在后体形成低速尾迹区；在跨声速情况下，流动上表面前缘形成范围更大的超声速流动区域，并在较强的逆压梯度作用下形成较大的低速尾迹区，且在减速伞下游形成了明显的结尾激波；在超声速情况下，来流在座舱前体形成前缘斜激波，并随马赫数的增加激波强度增大，激波面更靠近物面。另外，在不同马赫数条件下减速伞均处于座舱低速尾迹之外，能够提供高效的气动载荷。

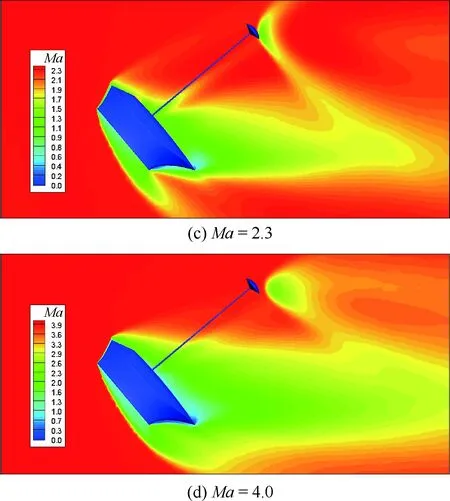
图11 攻角为50°时典型马赫数情况下整体式座舱+减速伞构型对称面流场马赫数云图Fig.11 Mach contour of symmetrical flow field of integral escape module with brake parachute for typical Mach numbers at angle of attack 50°

图12给出了Ma=0.7～4.0时整体式座舱+ 减速伞构型的纵向气动特性曲线。由于飞行攻角均不低于30°，该构型升力随攻角的变化规律偏离线性区，呈先增加后减小的趋势，如图12(a)所示；在大攻角情况下，随着迎风面的大幅增加，气动载荷在阻力方向的分量明显增大，且随攻角的增加而接近线性增大，如图12(b)所示；加之减速伞气动载荷在阻力方向的贡献，使得在俯仰力矩配平的情况下，整体式座舱+减速伞构型的阻力在宽速域范围内均得到明显提升，且高于6倍单独整体式座舱阻力，如图12(c)所示；俯仰力矩在该攻角范围内呈现近似线性递减的变化趋势，超声速情况下力矩配平攻角基本为52.7°，而亚声速基本为62.1°，如图12(d)所示；俯仰力矩随攻角的变化斜率在宽速域范围内均小于0，如图12(e)所示，可见改进后的座舱系统在该攻角范围内均具有静稳定的特性。

图13给出了Ma=0.7～4.0时整体式座舱+减速伞构型的横、航向气动特性曲线。侧力系数CY仍旧呈近似线性分布，且随侧滑角的增加而降低，如图13(a)所示。由于减速伞位于座舱重心后上方，当座舱受到横、航向扰动后，可为座舱提供抵制该扰动的力矩。因此在减速伞的辅助下，整体式座舱偏航力矩Cmz随侧滑角的增加而增加，而滚转力矩系数Cmx随侧滑角的增加而减小。采用最小二乘法对各曲线进行线性拟合，其斜率∂Cmx/∂β、∂Cmz/∂β如图13(d)所示，整体式救生座舱在整个弹射包线内，横、航向均具有静稳定性(∂Cmx/∂β<0、∂Cmz/∂β>0)。

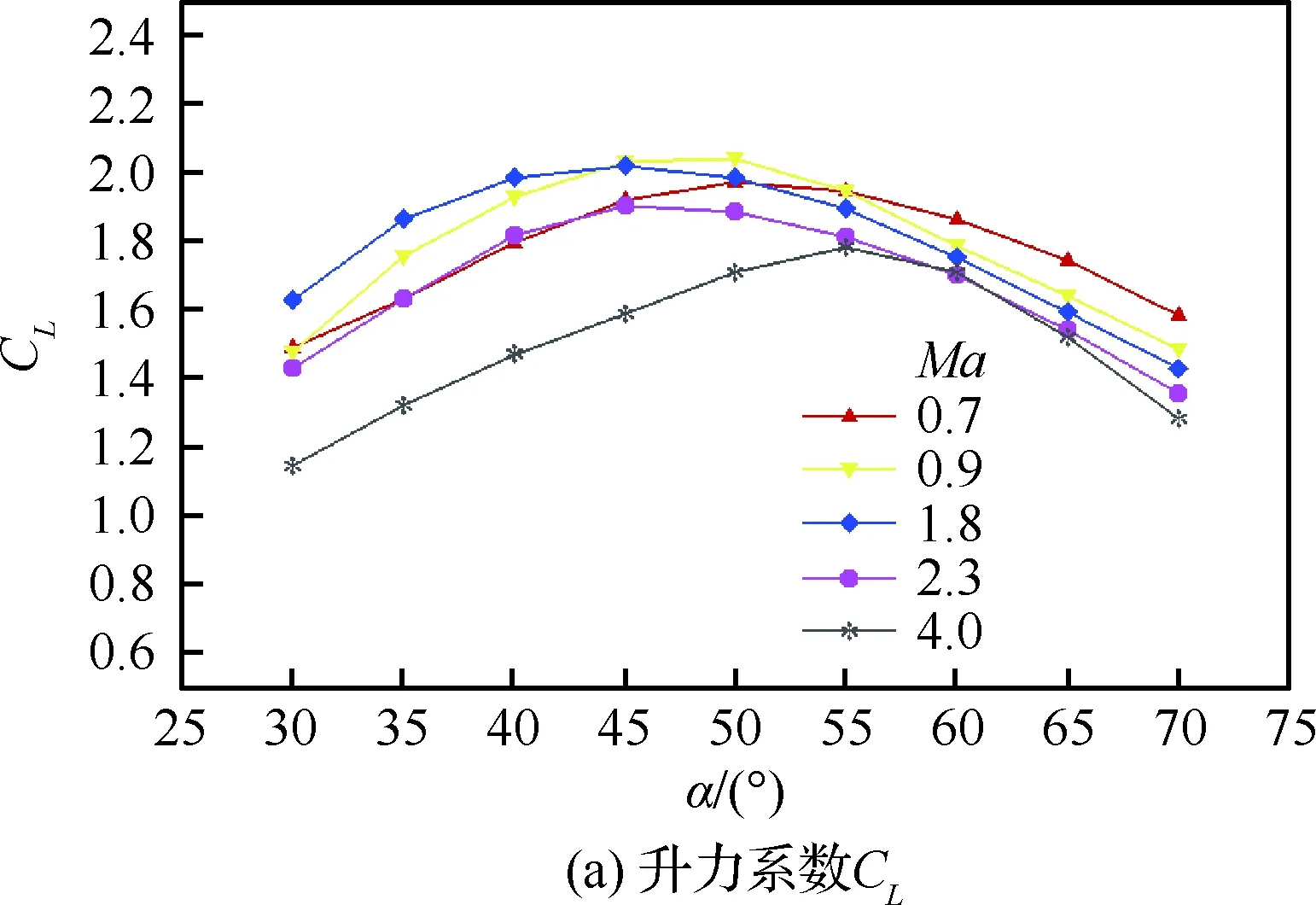
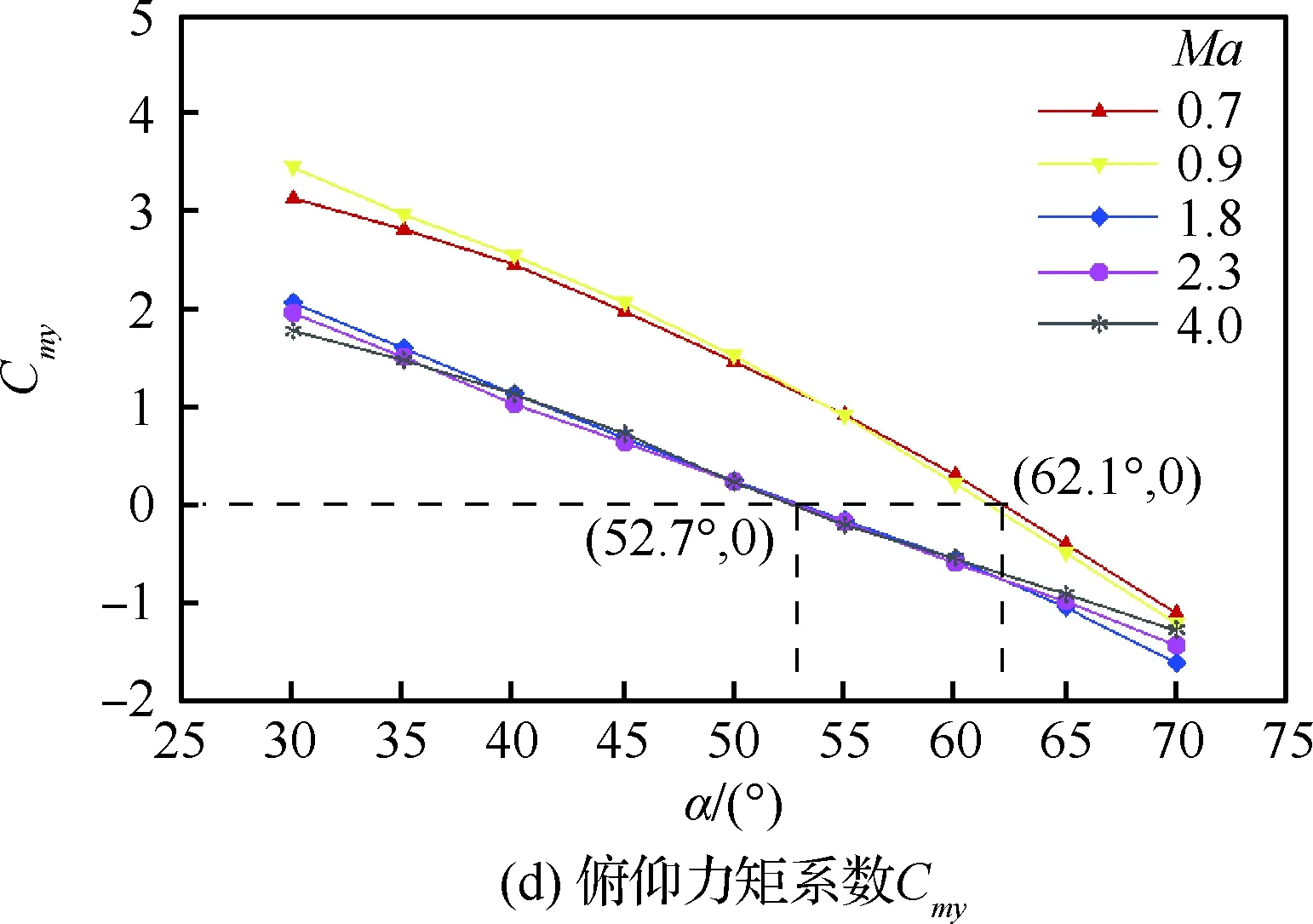
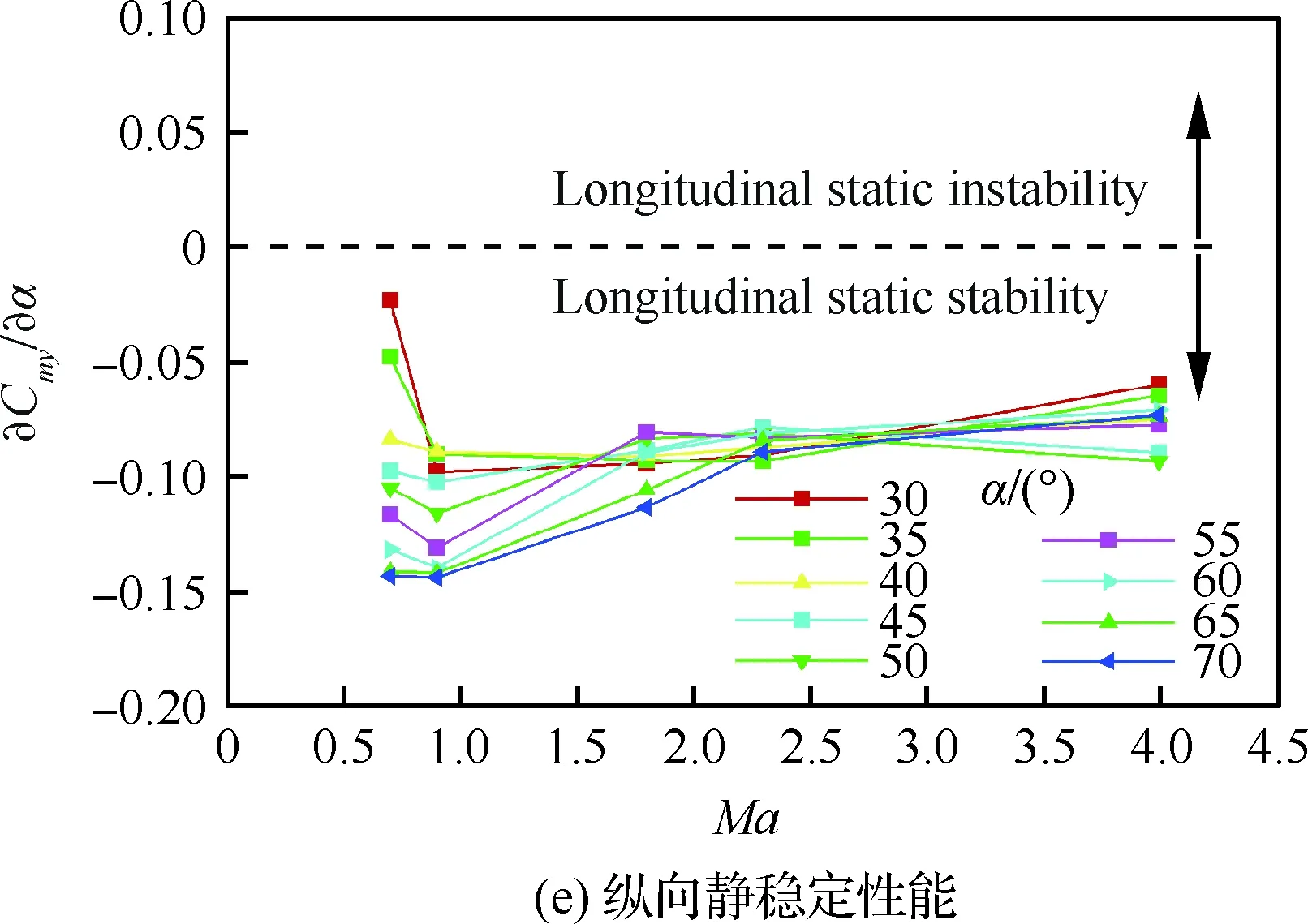
图12 整体式座舱+减速伞构型宽速域纵向气动特性曲线Fig.12 Longitudinal aerodynamic coefficients of integral escape module with brake parachute for wide Mach number range

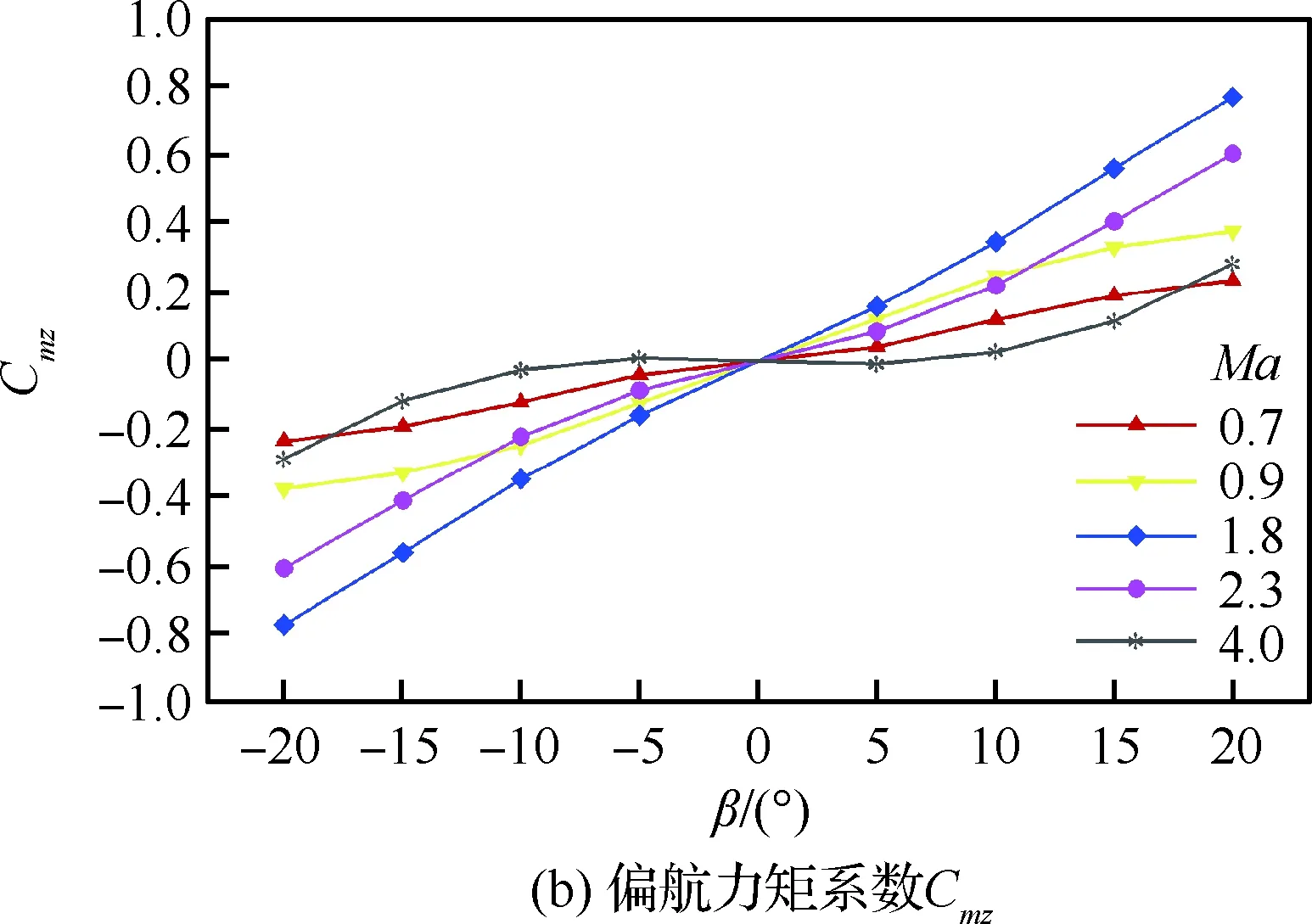
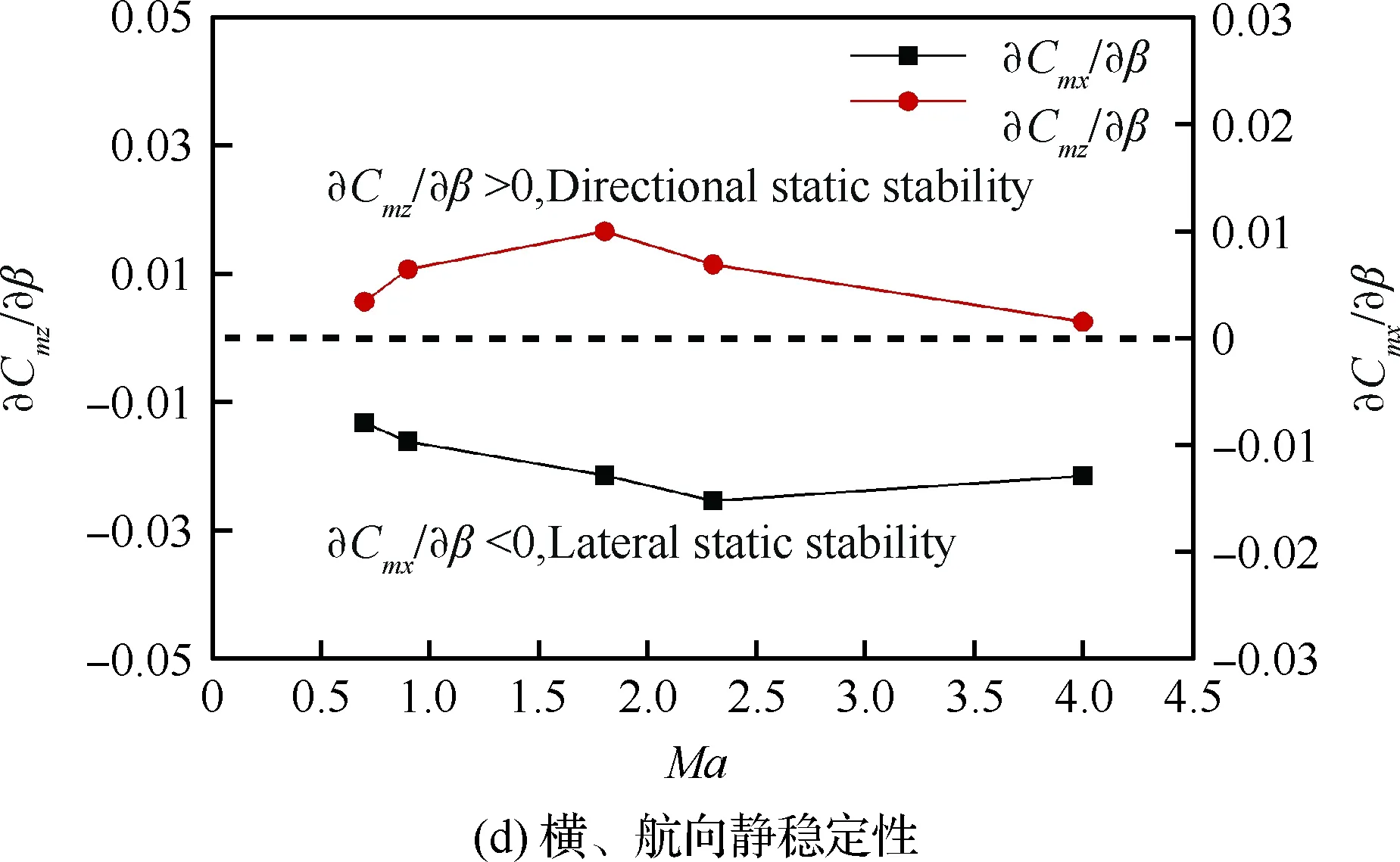
图13 整体式座舱+减速伞构型宽速域横、航向气动特性曲线Fig.13 Lateral and directional aerodynamic coefficients of integral escape module with brake parachute for wide Mach number range

总体来看，座舱在增加刚性减速伞之后，纵向、横向以及航向气动特性均得到了大幅改善，在宽速域范围内均具有静稳定性，同时阻力提升6倍以上，可为座舱的稳定减速提供良好的气动载荷保障。

4.3 动稳定性评估

为进一步评估座舱系统在抛投后的动态稳定性，采用动态数值模拟方法对座舱系统开展自由俯仰转动计算。计算网格分为两个部分：静止的外流场区域(Outer Field)和跟随座舱系统自由俯仰转动的流场区域(Inner Field)，如图14所示，两区域通过交界面(Interface)边界分开，并通过该边界进行数据传递；考虑座舱与机体分离后一般难以直接处于力矩配平姿态，所以将座舱初始姿态设置为30°，模拟座舱在处于非力矩配平状态后的自由俯仰转动特性。

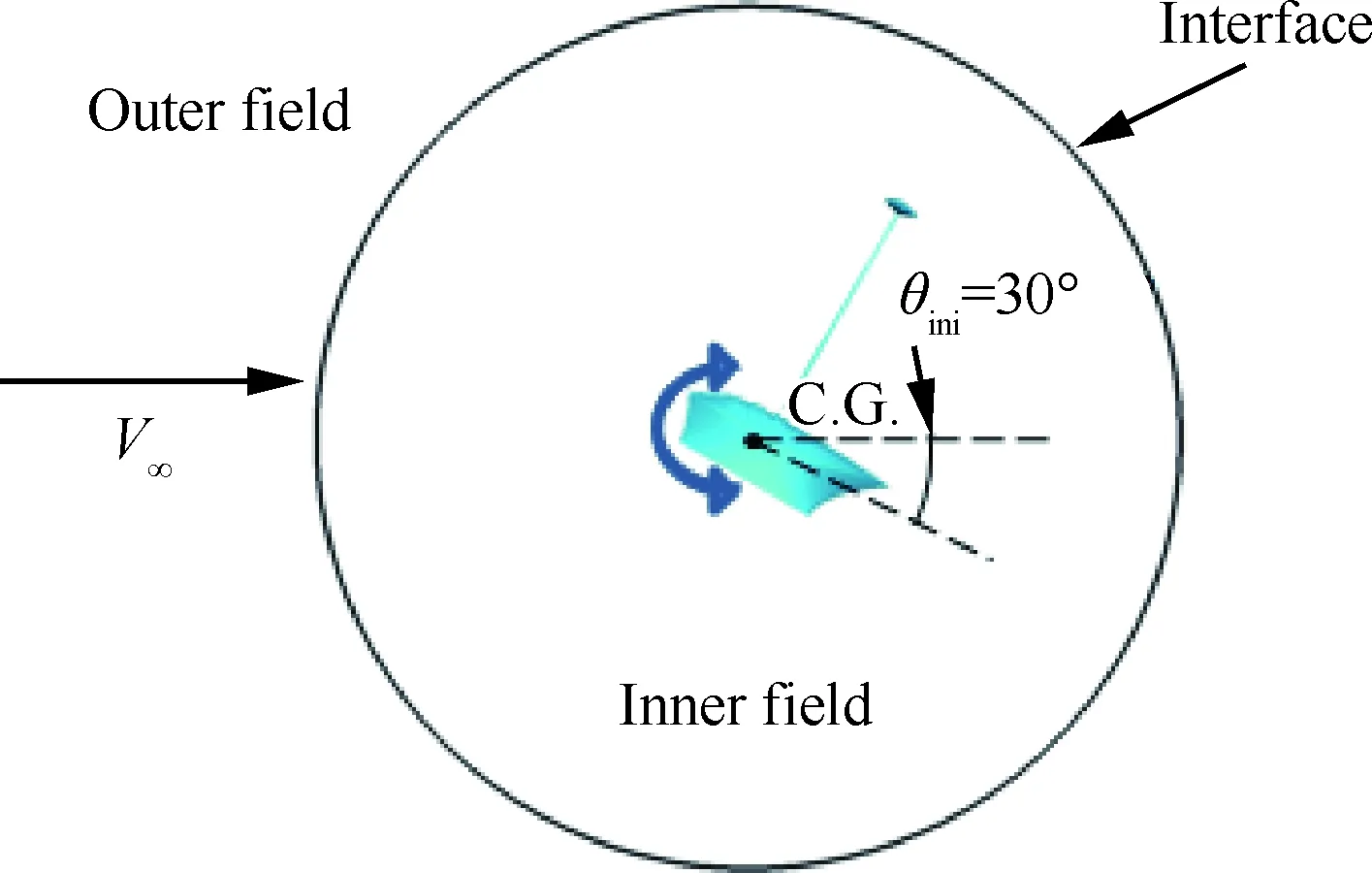
图14 整体式座舱+减速伞构型自由俯仰转动示意图Fig.14 Illustration of free pitching of integral escape module with brake parachute

图15给出了Ma=0.3～4.0时座舱系统在自由俯仰转动过程中的俯仰角曲线。在宽速域范围内座舱系统俯仰姿态均呈现减幅振荡的变化趋势，该系统具有动稳定性能；在亚声速情况下，随着马赫数的增大，座舱俯仰角振荡幅值和周期减小，阻尼增大；超声速情况下反之；对于Ma=4.0的情况，当飞行高度为30 km时，因来流动压较低，其俯仰角振荡收敛较为缓慢，而当飞行高度降低到18 km后，因飞行动压增加，座舱俯仰振荡的恢复力相应增加，使得俯仰角振荡幅值减小，同时由于大气密度的增加，阻尼较大，其振荡周期随之减小，姿态收敛较为迅速。

诚然，监狱和镣铐确实不是对思想的反驳。 那么什么东西可以反驳思想呢？可以用思想反驳思想，可以用理论反驳理论(尽管对理论的最好反驳是事实)。 什么东西可以反驳“瘙痒”的思想呢？很显然，已经被“瘙痒”打碎的理论无力承担这份责任。 我们知道，陀思妥耶夫斯基的“瘙痒”常被称为极端个人主义(ultra- individualism)，也可以称为个性自由(freedom of personality)的辩护。 罗扎诺夫想出来的对付“瘙痒”的方法，是另一种形式的“瘙痒”。 正是多种“瘙痒”的并存，肯定了自由的无限可能性。 他说：

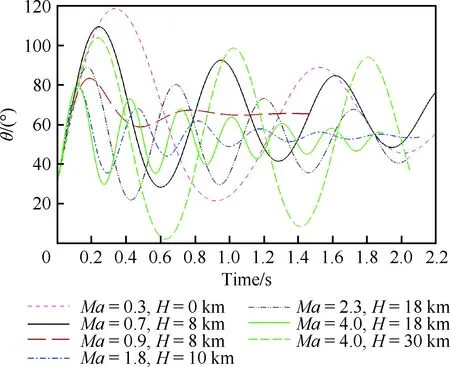
图15 整体式座舱+减速伞构型自由转动过程俯仰角变化Fig.15 Pitching angle variation during free pitching for integral escape module with brake parachute

通过刚性减速伞方案，整体式座舱在宽速域范围内获得了较高的动稳定性能。虽然座舱在马赫数较低(Ma=0.3)时姿态收敛较为缓慢，但该速度范围已经可以采用常规的降落伞方式辅助稳定落地；对于高马赫数(Ma=4.0)情况，座舱姿态也存在收敛缓慢的问题，此时可通过降低飞行高度的方式增加飞行动压，一方面增加座舱俯仰振荡的阻尼，加快姿态的收敛，另一方面增加座舱俯仰振荡的恢复力，降低俯仰振荡的幅值，从而改善座舱姿态的收敛特性。

5 整体式座舱系统分离轨迹仿真

第4节提出的刚性减速伞方案使座舱在宽速域范围内获得了静、动态稳定性，且具有高效的减速性能。第5节将针对该座舱系统的近机区抛投过程，采用动态重叠网格技术开展动态数值模拟，分析并验证座舱与机体分离的安全性。

5.1 座舱分离轨迹动态数值模拟方法

图16给出了近机区座舱系统的抛投过程示意图，共分为3个阶段：座舱沿滑道迅速弹出、火箭助推以及自由投放，各阶段具体参数可见表1。为保证座舱与机体安全分离，在滑道弹射和火箭助推阶段的外加载荷均远大于气动载荷，且作用时间短，所以在数值模拟过程中将这两个阶段采用指定运动的方式进行模拟；进入自由投放阶段后，以前两个阶段产生的位置、姿态、速度以及角速度作为初始值，开展自由抛投模拟，最终获得座舱系统抛投过程的整个轨迹特性。

计算网格如图17所示，由机体网格(背景网格)和座舱网格(子网格)两部分组成，并以座舱网格的外边界作为挖洞边界，将位于座舱网格区域内的机体网格挖掉，且挖洞位置将随座舱的运动而实时改变。为降低计算量，采用简化机体模型，主要考虑机体上表面形状对抛投过程的影响。

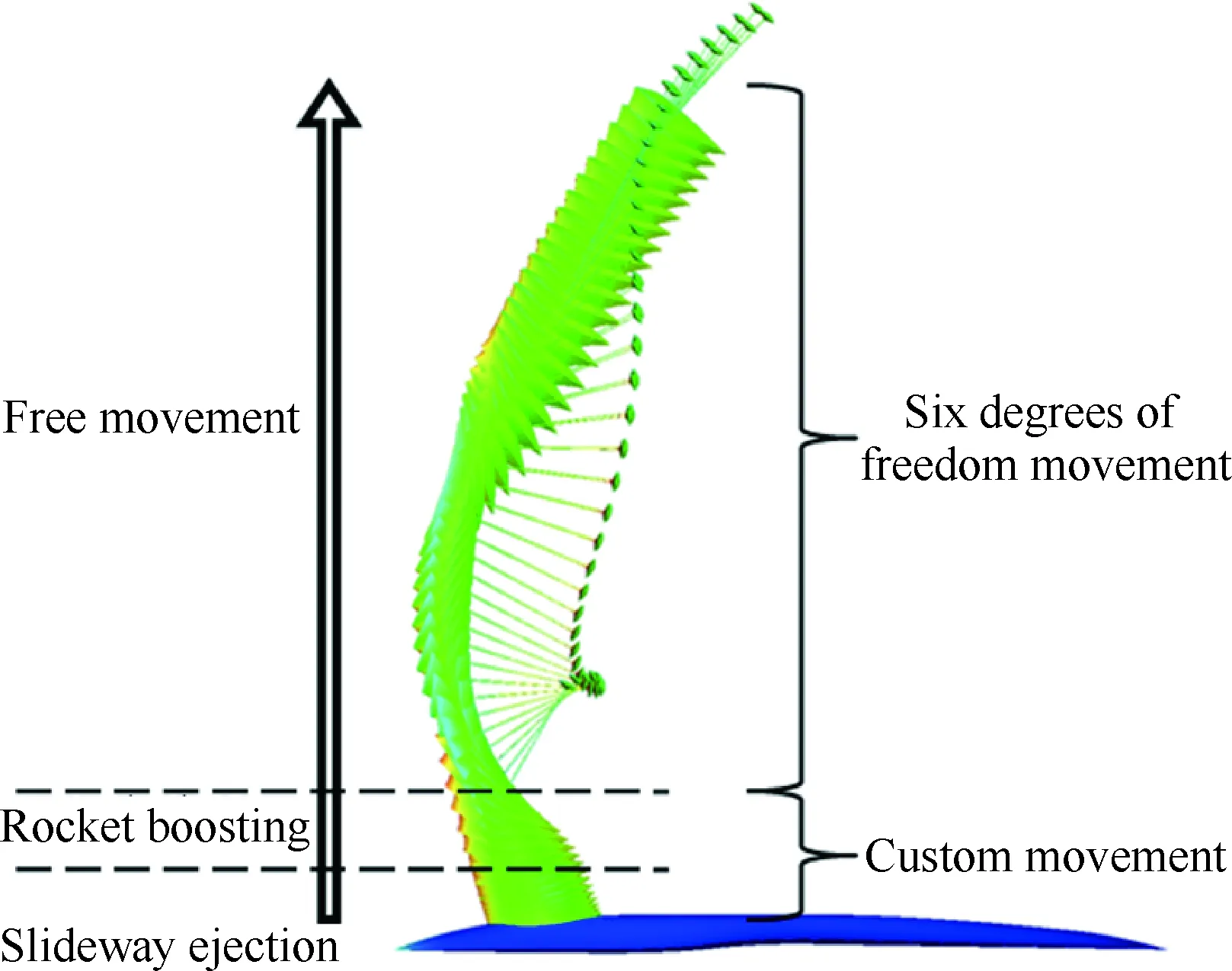
图16 整体式座舱+减速伞构型抛投过程示意图Fig.16 Illustration of separation stages of integral escape module with brake parachute

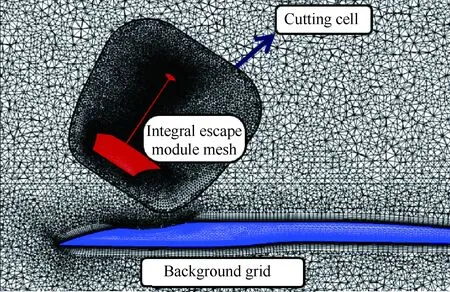
图17 带机体模型的整体式座舱+减速伞构型抛投计算网格Fig.17 Grid illustration of integral escape module with brake parachute and aircraft model

5.2 座舱轨迹特性分析

图18给出了典型马赫数情况下座舱抛投轨迹图，Ma=0.7时，座舱首先沿滑道直线弹出；然后在火箭助推作用下继续离开机体，同时在火箭助推抬头力矩和座舱前体高压区的作用下逐渐抬头；最后在打开减速伞后，座舱获得较大抬头力矩而继续迅速抬头，同时座舱后体物面压力变强以及减速伞气动力对座舱重心的力臂变小，使得俯仰角达到一定值后转为低头运动。其他马赫数情况下座舱轨迹和物面压力变化规律与Ma=0.7时的比较相近，但由于飞行环境和飞行动压的不同，其轨迹在姿态收敛速度和平移运动量等方面存在一定的差异。

图19给出了Ma=0.3～4.0时座舱系统抛投轨迹曲线。座舱抛投1.3 s后离机垂直距离z均高于7.98倍座舱长度LZC，座舱具有足够的离机距离，远离机体气动干扰区。轴向距离x(减速效率)和姿态随马赫数的变化规律与单独评估座舱+减速伞救生系统动稳定性的结论一致：亚声速时，随着马赫数的增加，轴向距离x随之增加，俯仰角振荡收敛，且周期和幅值均随之减小；超声速时反之，但由于Ma=4.0时采用低空(H=18 km) 抛投，动压及空气密度大幅增加，其轴向距离明显增大，俯仰角θ收敛速度明显增快且振荡幅值大幅降低。

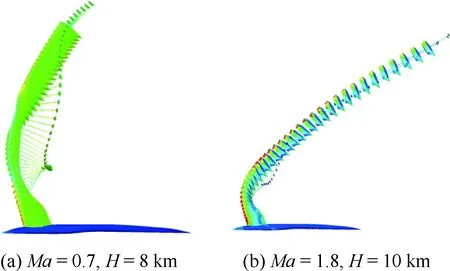
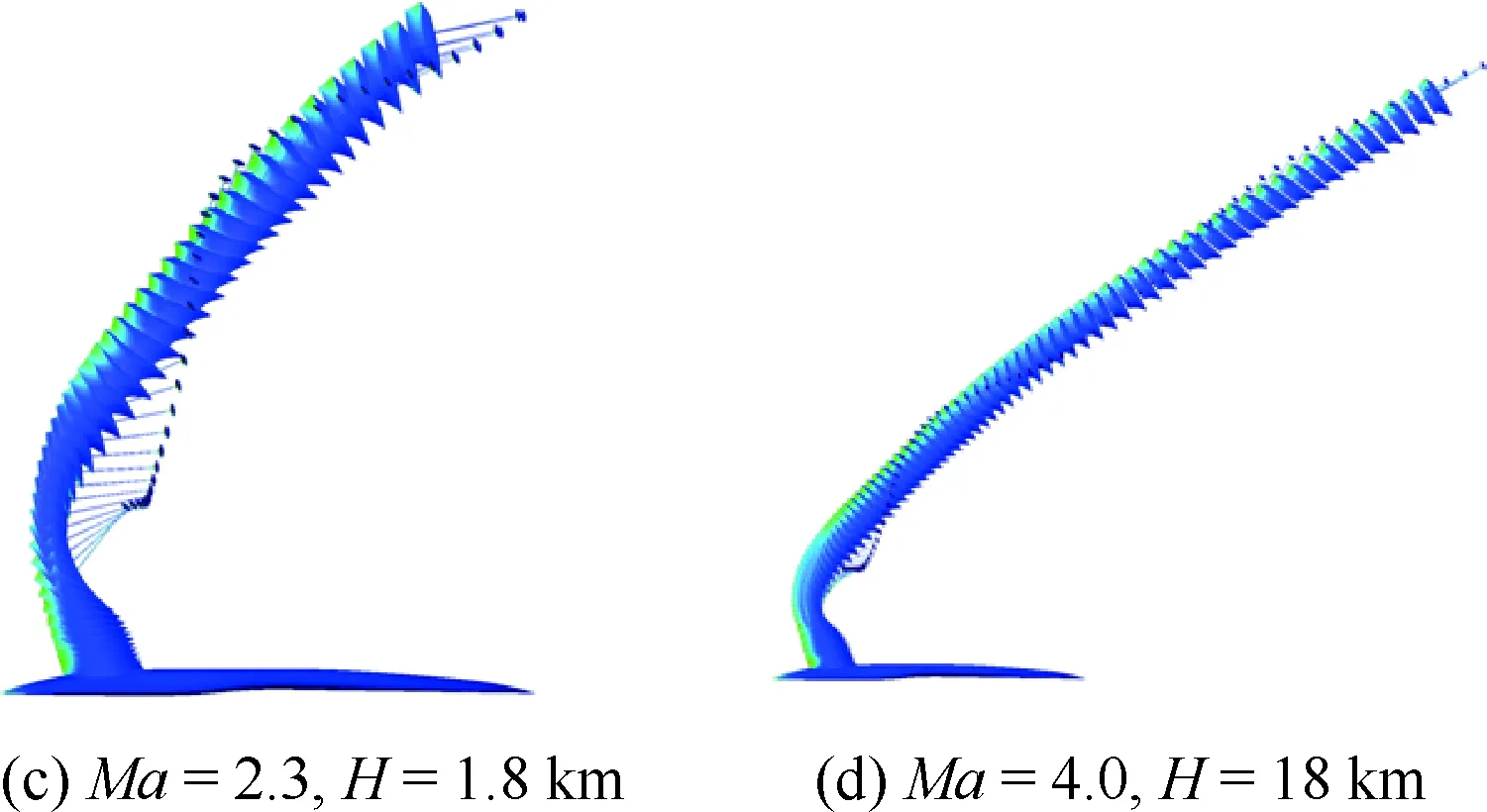
图18 典型马赫数情况下整体式座舱+减速伞构型抛投过程轨迹Fig.18 Separation trajectory of integral escape module with brake parachute at typical Mach numbers

图19 宽速域整体式座舱+减速伞构型抛投过程轨迹Fig.19 Separation trajectory of integral escape module with brake parachute for wide Mach num-ber range

在宽速域范围内，带刚性减速伞的座舱系统均能安全抛离机体，且在离机后具有姿态收敛的稳定特性，为抛投后座舱的安全着陆提供可靠的气动保障。

6 结 论

首先，针对空天飞行器提出了一种整体式救生座舱系统，并采用减速伞方案对其稳定性和减速效率进行了改善；然后，采用基于动态重叠网格方法的自研数值模拟平台ARI-OVERSET对整体式座舱+减速伞构型纵向抛投近机轨迹特性开展了动态数值模拟计算。研究结果表明：

1) 对于研究的单独整体式座舱，气动性能在纵向、横向以及航向均出现静不稳定问题(∂Cmy/∂α>0、∂Cmx/∂β>0以及∂Cmz/∂β<0)，且纵向静不稳定性随着马赫数、攻角的增加而恶化。

2) 通过刚性减速伞方案，座舱系统(整体式座舱+减速伞构型)静、动稳定性和减速效率均得到大幅改善。在减速伞气动载荷的作用下，座舱气动焦点后移，在Ma=0.3～4.0飞行包线内均具有静、动稳定性；在亚声速情况下，随着马赫数的增大，座舱俯仰角振荡幅值和周期减小，阻尼增大，而超声速情况下反之，但高马赫数(Ma=4.0)时可通过降低飞行高度的方式进一步提升座舱动稳定性；另外，减速伞抬头力矩使座舱在超声速情况下的力矩配角攻角为52.7°，而亚声速情况下为62.1°，从而使座舱减速效率提升6倍以上(即阻力载荷提升6倍以上)。

3) 在宽马赫数飞行包线内，整体式座舱+减速伞救生系统弹射过程中，通过近机区的动态数值模拟分析可知，在弹射力和火箭推力的辅助下，座舱构型能够实现安全分离，其姿态收敛特性随马赫数的变化规律与单独评估整体式座舱+减速伞构型动稳定性的结论一致，具有收敛特性。