强迫扰动下的射流撞击雾化特性

李佳楠，雷凡培，杨岸龙，周立新

1. 西安航天动力研究所 液体火箭发动机技术重点实验室，西安 710100 2. 中国船舶集团有限公司，北京 100097

燃烧不稳定是液体火箭发动机研制过程中经常遇到的重大技术问题[1]，其重要特征表现为燃烧室中与声学固有振型一致的大幅值背压振荡，振幅达到稳态室压的10%～100%，振荡频率从数百Hz到15 000 Hz以上[2]。燃烧不稳定会导致发动机极高加速度的机械振动，对发动机的机械系统造成破坏，还会破坏推力室内的冷却系统，导致超高热流流向喷注器以及壁面，引起内壁面的烧蚀，对发动机造成毁灭性打击。由于燃烧不稳定自身复杂的耦合特性，以及推力室高温、高压、高热流难以获取数据的恶劣环境，人们对燃烧不稳定的激发、维持机理仍没有清晰的认识，喷雾燃烧的各个物理化学子过程都有可能成为燃烧不稳定激发与维持的关键子过程。

研究燃烧不稳定的方法有自发激励与强迫响应2种方式[3]，自发激励必须考虑燃烧室中所有的物理化学过程，强迫响应则是通过在边界施加扰动，研究强迫扰动下的喷雾燃烧过程。自发激励的优点是完全揭示了燃烧火焰与背压振荡之间的激发与反馈机理，强迫响应的优点则在于可以研究各种不同的子过程对于不同振幅、不同频率的声学压力振荡的响应。相关研究表明雾化不仅影响稳态的燃烧过程，而且与燃烧不稳定的激发、维持有着千丝万缕的联系。撞击式喷嘴的Hewitt准则[4-6]表明，撞击式喷嘴燃烧稳定性由2个重要参数控制，一是射流直径，二是喷射速度。通过改变喷射速度可以改变发动机的稳定性阈值，实现发动机由稳定向不稳定的转变，Hewitt准则预测的稳定性边界与多种全尺寸发动机的实际工作特性十分吻合[6]。Qin等[7]通过数值计算发现，液滴粒径分布与空间分布对燃烧不稳定产生重要影响，局部聚集的细小液滴会形成局部准定容燃烧过程，并在推力室空间内形成压力尖峰，空间随机产生的压力尖峰最终会诱导出声学振型，产生燃烧不稳定，在这个过程中，喷雾是最为关键的环节。Bai等[8]发现，喷雾自激振荡必然引起火焰振荡以及燃料喷前压力的振荡，当自激振荡的频率与燃烧室的固有频率一致时，会诱发燃烧室的压力振荡，表明雾化的自激振荡是发生不稳定燃烧的非常关键的诱因。本文将采用强迫响应的方法研究强迫扰动条件下的射流撞击雾化特性。

为了揭示燃烧不稳定复杂的耦合机理，国内外的研究机构采用试验或者数值模拟的方法开展了声学振荡下的喷雾或者燃烧特性研究。Baillot等[9]试验研究了横向声场作用下的气液同轴剪切喷嘴的雾化特性，当射流位于速度波腹位置时，在非线性声辐射压力的作用下，射流由圆柱液体变为扁平液膜，液核长度减小，并且破碎更加剧烈。当推力室内多个喷嘴的雾化特性同时改变时，非稳态燃烧过程会发生显著变化，就有可能激发出燃烧不稳定。Carpentier等[10]在Kundt管中研究了横向声学压力振荡对于单束射流的影响，当射流位于压力波腹位置时，射流的形态几乎没有发生变化。而当射流位于速度波腹位置时，与Baillot等[9]观察到的现象类似，射流变为扁平液膜。当射流位于压力波腹与速度波腹之间时，射流在非对称声辐射压力的作用下发生偏转。Ficuciello等[11]开展了横向声学振荡条件下气液同轴射流的雾化试验，进一步验证了声学振荡对于雾场的直接作用，发现了声学耦合作用下的液滴聚集现象，并基于非线性声学理论对试验观察到的现象进行了阐释。Hardi等[12]开展了低温液氧射流试验，当存在横向声学振荡时，液氧的液核长度减小了近70%。为进一步揭示声波对于雾化过程的影响，基于气液两相流大涡模拟算法，Rutard等[13]开展了亚临界条件下气液同轴剪切喷嘴在横向振荡压力场下的雾化特性数值模拟，同样发现了射流扁平以及液核缩短的现象，并分析了横向声学振荡对于喷雾动力学以及液滴粒径的影响。Dighe和Gadgil[14-16]研究了横向声波对于射流撞击形成液膜破碎的影响，结果表明垂直于液膜的声学压力振荡促进了液膜的破碎，生成的液滴数目增多，液滴平均粒径减小。Hakim等[17]采用大涡模拟研究了横向声学扰动条件下低温推进剂的火焰特性，当火焰位于速度波腹位置时，火焰长度也会减小，并且变成扁平，同时在速度波腹位置出现周期性振荡的现象，这与横向压力振荡条件下观察到的冷态喷雾场有些类似。

笔者团队[18]总结出了背压振荡影响撞击雾化的两种作用机制，背压振荡除了对喷雾燃烧产生直接作用外，还会通过改变喷注压降影响喷射过程，进而对后续的雾化、燃烧等子过程产生影响。当推力室中出现纵向的不稳定或者喷嘴位于横向不稳定的压力波腹位置时，这种机制将会成为背压振荡影响雾化的主要作用机制，这也是本文重点关注的问题。当喷注压降周期性变化时，喷射速度也会发生周期性改变，此时，运动速度较快的流体就会追击运动速度较慢的流体，从而使流体在空间呈现出堆积的现象，这就是Klystron效应[19-20]。由系统动力学分析[21-22]可以证明，燃烧室的压力振荡与管路中的压力振荡都会引起喷射速度的周期性变化，二者在幅值与相位上存在定量关系，在一定程度上可以等效处理，由于后端扰动的研究开展较为困难，可以开展前端扰动下的雾化试验。

Crane等[23-24]设计了机械扰动装置，研究了前端压力扰动对射流破碎的影响，建立了扰动频率、幅值与射流破碎长度的关系，对低速射流破碎的Rayleigh分析作了改进，发现在强迫扰动的作用下，低速射流破碎机理由表面张力主导向Klystron效应主导转变。Chigier[25]应用压电式驱动装置对射流前端施加扰动，同样也发现了Klystron效应，射流速度的周期性变化导致射流形态出现圆盘状的结构，在射流本征频率附近的扰动能增加液滴尺寸的均匀性。康忠涛等[26]采用水力扰动装置研究了有/无振荡2种情况下气液同轴离心式喷嘴自激振荡的喷雾形态。在理论分析方面，Heister等[27]采用边界元方法(BEM)研究了气体纵向振荡条件下的射流过程，纵向扰动会使射流速度发生周期性变化，周期性扰动的速度会导致射流形成Klystron效应，通过不同频率的扰动速度分析发现，射流对其本征频率处的扰动响应最强。在数值模拟方面，Srinivasan等[28-29]基于OpenFOAM，应用VOF(Volume of Fluid)界面捕捉方法实现了射流破碎的数值模拟，通过在射流入口给定正弦的扰动速度，研究了射流平均速度以及速度扰动的频率、幅值对射流破碎的影响。数值模拟研究表明，在相同的Strouhal数下速度扰动振幅对射流破碎产生显著影响，增加振荡振幅和频率都能够增加射流的喷雾锥角。Yang和Turan[30]基于开源程序Gerris[31-32]，研究了低速与高速条件下，扰动频率、幅值对于射流雾化的影响。对于低频与中频扰动而言，随着扰动频率的增大，未受扰动的射流长度将会减小，液滴平均粒径将会增大。对于高频扰动而言，雾化特性参数则变化较小，表明射流对高频扰动的响应不敏感。扰动幅值对于液滴数目以及液滴粒径具有重要影响，扰动幅值增大，液滴数目将会增大，而液滴平均粒径将会减小。参照Bazarov等[33]设计的压力扰动装置，Yang等[34-35]设计了前端压力扰动装置，通过对喷前压力施加扰动，试验研究了喷射流量变化的Klystron效应对撞击雾化的影响，本文将在前人的基础上继续对强迫扰动下的撞击雾化过程开展系统深入的研究。

对雾化过程的研究，传统上主要采用试验的方法开展，而与试验相比，数值模拟具有独特的优势，可以对液膜、液丝的破碎过程进行细致的观察，捕获有效的数据信息，还可以对试验现象进行深入分析，揭示试验现象背后所蕴含的物理本质，本文将采用数值模拟与试验结合的方法开展研究。雾化过程属于多相、多尺度的流动过程，需要处理相界面追踪、自由界面大变形等问题，对网格尺度、时间尺度要求很高，计算量很大。本文采用的数值模拟方法在处理雾化这种多相、多尺度的流动过程中具有诸多优势：采用树形自适应加密算法对空间进行离散，同时结合分段线性的VOF方法，在实现相界面精确捕捉的同时，与固定网格相比显著降低了计算量，时间步长也随网格尺度相应调整，实现了时间尺度自适应；由高度函数结合连续表面力模型实现表面张力的精确求解，这在雾化过程的数值计算中尤为重要。

关于撞击式喷嘴的雾化机理及雾化特性，国内外已经开展了大量的研究工作，基本掌握了其在稳态条件下的工作特性，但对于其在非稳态条件下的雾化特性目前还知之甚少，导致发动机设计中无法全面准确把握该种型式喷嘴的喷雾特性。当发动机在工况调节状态下工作或出现燃烧不稳定性时，因无法掌握其喷雾特性而给性能评估以及故障分析和定位造成严重阻碍。由于燃烧不稳定是极其复杂的物理化学过程，本文将重点关注背压振荡影响撞击雾化第一种机制，采用试验结合数值模拟的方法研究喷射速度的周期性变化对于撞击雾化特性的影响，这对于进一步认识雾化在燃烧不稳定中所起的作用以及揭示燃烧不稳定机理都将起到积极的推动作用。

1 试验系统

首先介绍一下试验系统，试验系统主要由高压水路供应系统、水力扰动装置、撞击式喷嘴、脉动压力数采系统、高速摄影系统以及同步触发装置组成，其结构示意图如图1所示。液体贮箱内的工质水经过高压氮气挤压之后分为两路，一路流经撞击式喷嘴完成雾化过程，另一路流经水力扰动装置排出。

水力扰动装置是产生喷前压力扰动的核心部件，其结构示意图如图2所示，主要由定子与转盘两部分组成，定子与转盘相互贴合。转盘边缘沿周向均匀布置一圈小孔，由电机带动转动，当转盘上的孔与定子的孔重叠时就有流体流经扰动装置，当定子上的孔被完全遮挡时，就没有流体流经

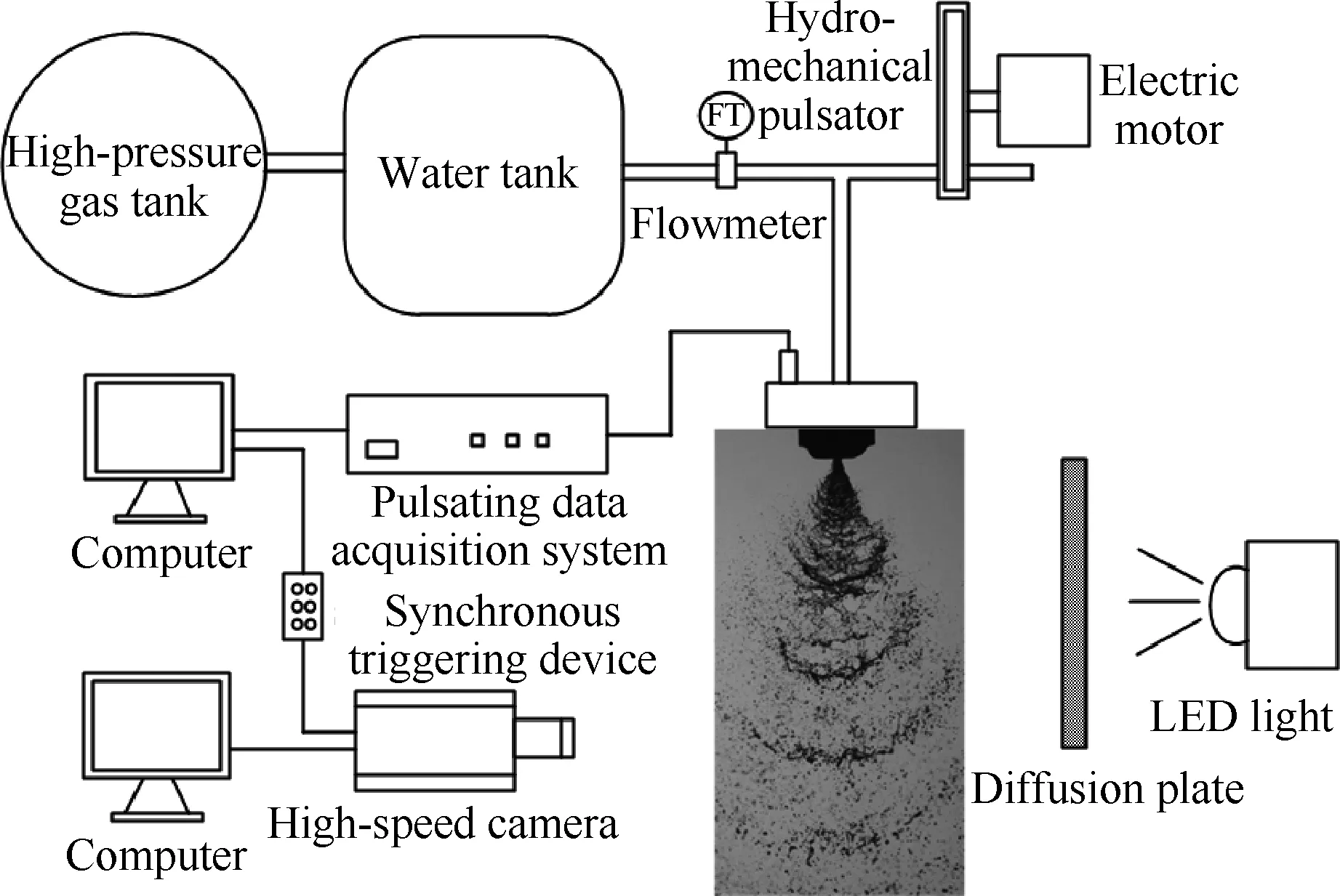
图1 试验系统结构简图Fig.1 Sketch of test system

扰动装置，由此来产生喷前压力的扰动，通过调节电机转速来改变压力扰动的频率，试验达到的最高频率约为3 563 Hz。

由Kistler脉动压力传感器采集喷前的脉动压力，由XP5压力传感器记录周期性变化的喷注压降，采样频率均设定为20 480 Hz。由高速摄影对雾场进行背光拍摄，设定高速相机的拍摄频率为每秒拍摄20 480张图片，图像分辨率为512 pixel×512 pixel。通过同步触发装置实现脉动压力测量与雾场拍摄的同步，同步测量的原理为脉动压力传感器对脉动压力不间断采集，由信号发生器产生一个阶跃信号触发高速摄影工作。高速摄影触发的时间精度为2 μs，DG535信号发生器的时间精度为ns量级，而数采系统采样的时间精度为10 μs，根据木桶原理整个同步触发装置的时间精度应为10 μs，目前试验所做的最高扰动频率约为3 563 Hz，10 μs的时间精度等级可以满足试验需求。

试验采用的撞击式喷嘴结构示意图如图3所示，两束圆柱射流轴线的交点定义为撞击点，液体工质加压喷射之后在撞击点处相互撞击完成雾化

图3 撞击式喷嘴结构示意图Fig.3 Sketch of impinging jet injector

过程。图3中标注了撞击式喷嘴的部分结构参数，选用了射流直径d为1 mm与0.8 mm两种孔径的喷嘴，撞击角2θ=60°，喷嘴出口到撞击点的喷射距离L约为6.9 mm。

2 数值模拟方案及算例验证

2.1 数值模拟方案

基于开源程序Gerris[31-32]实现两股射流撞击雾化过程的数值模拟，Gerris已在多种不同结构形式的喷嘴雾化[36-38]中得到应用，将采用的数值模拟方案描述如下。由八叉树结构形式的笛卡儿网格对空间进行离散，结合自适应加密算法实现特定区域的局部加密。由有限体积法直接数值求解不可压Navier-Stokes方程组，由分段线性的VOF方法对气液界面进行重构。表面张力采用Brackbill等[39]提出的CSF(Continuum Surface Force)方法，将相界面上一定宽度区域的表面张力等效为连续的体积力，在动量方程中加入这一项。湍流的处理采用隐式大涡模拟方法[40-41]，由数值黏性充当亚格子黏性模拟亚网格尺度的涡耗散。基于Linux系统，以MPI(Message Passing Interface)为并行平台实现三维两相流的并行计算。由于采用了动态的自适应网格，为了提高计算效率，采用了动态负载平衡技术。

图4 数值模拟计算域Fig.4 Computational domain of numerical simulations

求解的三维不可压Navier-Stokes方程组为

(1)

(2)

(3)

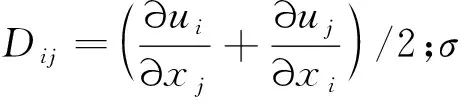
采用经典的VOF方法[42]对气液界面进行重构，在流场中引入体积分数α的概念，表征某一网格内第一相流体体积与网格体积之比：α=1表示该网格内充满第一相流体；α=0表示网格内充满第二相流体；0<α<1表示网格内存在两相流体，故存在自由界面。由于体积分数的引入，密度的对流方程式(1)可以等效为体积分数α的对流方程

(4)

流体的密度及黏度系数由网格内2种流体的体积分数加权计算

ρ=ρlα+ρg(1-α)

(5)

μ=μlα+μg(1-α)

(6)

式中：ρl与ρg分别为液相与气相的密度；μl与μg分别为液相与气相的黏度系数。

VOF方法的一个优点是不需要对界面的破裂、融合等现象作特殊的处理，因为这些拓扑结构的改变都隐式地包含在VOF方法中[43]。因此，VOF方法非常适合应用于存在诸多破碎、聚合现象的雾化过程的计算。

采用经典的时间分裂投影方法对控制方程进行离散，离散后的方程为

(7)

(8)

(9)

(10)

同时需要求解泊松方程

(11)

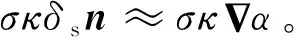
2.2 算例验证

关于Gerris计算稳态撞击雾化的算例验证工作在相关文献[36,44]中已经开展过，本文将进一步验证建立的数值模拟方案计算非稳态撞击雾化过程的有效性。对试验工况进行数值模拟的关键是获得喷嘴出口的周期性变化速度，以此作为数值计算的边界条件。现有的流量计都是稳态流量计，无法获得高频脉动的喷射速度，将通过流量压降的关系计算高频脉动的喷射速度。验证算例采用直径为0.8 mm的喷嘴，由XP5表压传感器记录得到随时间周期性变化的喷注压降，由于测量点与喷嘴出口距离较近，忽略流体惯性产生的时滞，并假定喷嘴的流量系数不随喷注压降的变化而变化。由压降与流量的计算公式(12)得到喷嘴的周期性变化流量。由式(13)换算成喷嘴出口的周期性变化速度u。要得到周期性变化的喷射速度还需要标定喷嘴的流量系数Cd，由式(12)可以看出喷嘴流量的平方与喷注压降呈线性关系，可以记录一系列一一对应的流量与压降，通过曲线拟合得到流量系数。

(12)

(13)

XP5表压传感器记录得到的周期性变化的喷注压降如图5所示，经过曲线拟合可近似认为喷注压降为正弦形式的振荡。喷嘴流量系数的标定曲线如图6所示，与上述分析一致，流量的平方与喷注压降近似呈线性关系，经过拟合可以得到喷嘴的流量系数Cd≈0.555。最终得到的喷嘴出口喷射速度随时间的变化如图7所示，喷嘴出口的周期性变化速度可以写成式(14)的形式，其中平均喷射速度u0=16.1 m/s，速度脉动幅值u′=0.186，扰动频率f=1 257 Hz。

u=u0(1+u′sin(2πft))

(14)

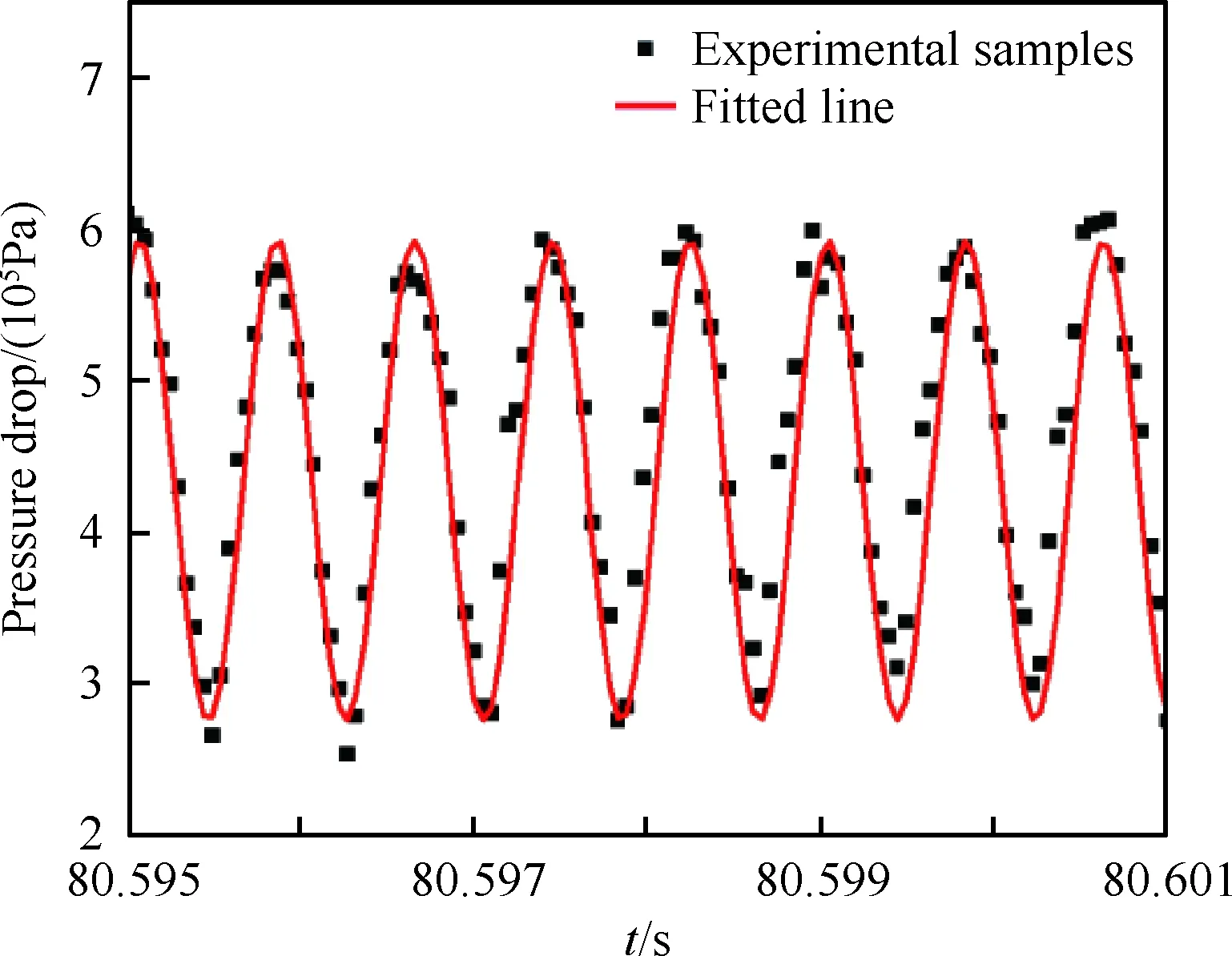
图5 压降信号与拟合曲线Fig.5 Pressure drop signals and fitted line

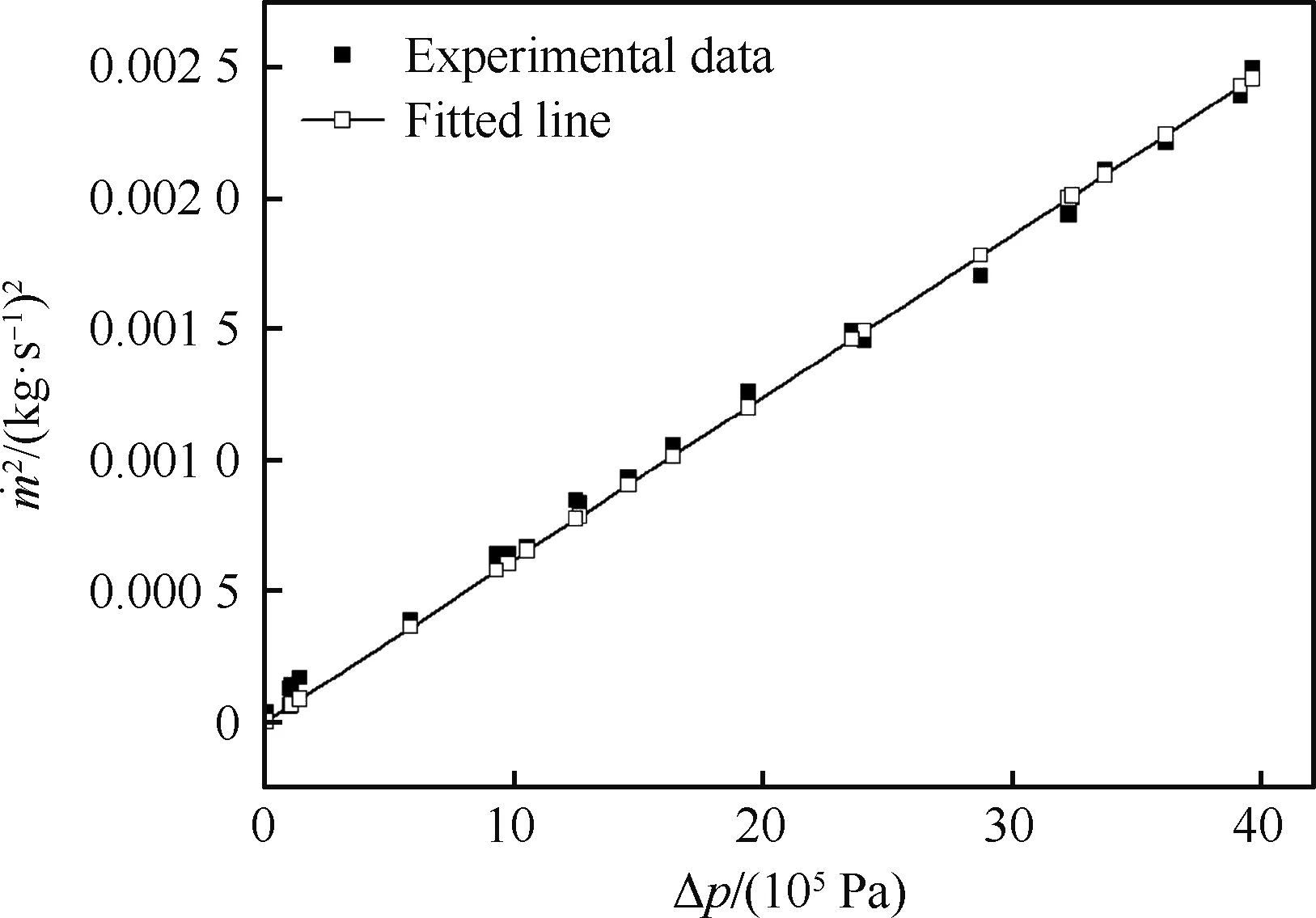
图6 流量与压降的对应关系Fig.6 Relationship between mass flow rate and pressure drop

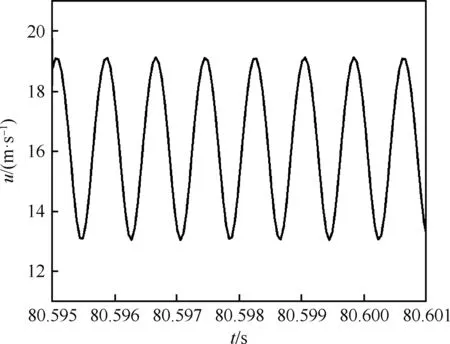
图7 周期性变化的喷射速度Fig.7 Periodically varying injection velocity

由上述得到的周期性变化速度作为数值模拟的边界条件，基于2.1节建立的数值模拟方案开展数值模拟。首先进行网格无关性验证工作，分别设定网格最高加密等级为7级、8级与9级，对应的最小网格尺度分别为234 μm、117 μm与58.6 μm，计算得到的撞击式雾场分别如图8所示。当网格分辨率较低时，数值模拟捕捉到的液滴尺寸较大，无法准确捕捉液膜的波动破碎过程，同样无法辨识雾化的Klystron效应。随着网格分辨率的提高，计算得到的雾场结构越来越精细。当网格最高加密等级为9级的时候，数值模拟能够捕捉到雾场中液膜、液丝、液滴等精细结构，同时也捕捉到了非稳态雾化中周期性液滴群聚集现象。因此最高加密等级为9级可以满足雾场空间发展对网格分辨率的要求，这与文献[45]中网格无关性验证的结论一致，在后续的数值模拟中设定网格的最高加密等级为9级。

计算得到了两束射流从喷射到撞击形成液膜，液膜波动破碎形成弓形液丝，弓形液丝进一步收缩形成液滴的完整雾化过程，整个过程与Anderson等[46]建立的三步雾化模型完全一致。数值模拟结果与试验结果的对比如图9所示，图9(a)为雾场正面的对比，图9(b)为雾场侧面的对比。从宏观上看，计算得到的雾场结构与试验拍摄的雾场结构是非常接近的。雾场正面形成以撞击点为顶点的具有一定喷雾角的雾化区域，雾场侧面液膜在撞击波的作用下波动破碎，并且在周期性变化的喷射速度作用下调制出Klystron效应，雾场下游出现周期性脱落的大尺度液丝，在3.1节将重点分析强迫扰动下的撞击雾化特性。图10展示了计算得到的非稳态喷雾场结构，根据试验以及数值模拟结果，其喷雾场可以大致划分为2个区域，即一次雾化区域与二次雾化区域。一次雾化区域主要包含液膜破碎的区域，液膜初步破碎形成了大尺寸的液丝以及大颗粒的液滴，是相对粗糙的雾化区域。二次雾化区域则更靠近雾场的下游，液丝与大颗粒液滴在气动力以及表面张力的作用下进一步收缩破碎形成更小尺度的球形液滴，雾化最终形成的液滴尺寸不仅取决于一次雾化形成的大颗粒液滴尺寸，还取决于二次雾化形成的小颗粒液滴尺寸。

图9 数值模拟喷雾图像与试验的对比Fig.9 Comparison of spray images between simulations and tests

图10 数值模拟得到的非稳态喷雾场Fig.10 Unsteady atomization field from numerical simulations

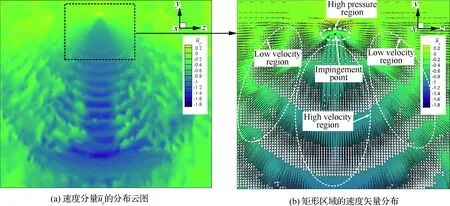
图11 YZ平面的速度分布Fig.11 Distribution of velocity on plane YZ

雾场沿XY截面与YZ截面的体积分数分布灰度图分别如图12(a)和图12(b)所示，黑色区域的体积分数为0，是气相区域，白色区域表示体积分数为1，为液相区域，气液界面处的体积分数0<α<1。 从两幅图中都可以明显观察到液膜的波动特性，液膜向下游运动过程中，在Kelvin-Helmholtz不稳定的作用下发生破碎。在图12(a)中定义了液膜的破碎长度与撞击波的波长λ，其中液膜破碎长度是一个动态的概念，液膜完全破碎之后，射流撞击形成液膜的破碎长度定义为撞击点到液膜完全破碎位置的距离。从图12(a)可以看出随着与撞击点距离的增加，液膜的波动幅值在逐渐增大，达到破碎的临界条件之后就开始破碎形成液丝。由于喷射速度是周期性变化的，速度较快的流体会追击速度较慢的流体，数值模拟也捕捉到了射流中流体堆积形成的“鼓包”结构。由图12(b)可以看出，液膜下游黑色与白色区域交替出现，这正是由于液膜的波动造成的，并且在越靠近下游的区域，弓形液丝的厚度也在减小，表明液膜在向下游运动过程中厚度是在不断减小的，这也是造成液膜不稳定性的另外一个因素[47]。在液膜破碎之后的下游区域，由于雾化的Klystron效应出现了大尺度的弓形液体结构。

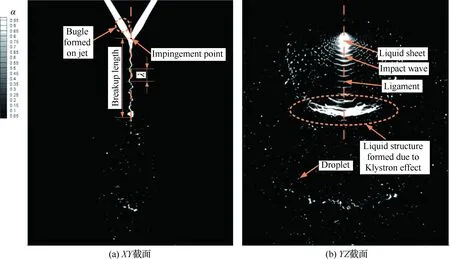
图12 不同截面的α灰度图Fig.12 Grayscale images of α of different slices

图13 液膜破碎区域速度分量的分布云图Fig.13 Contour of velocity component of liquid sheet breakup region

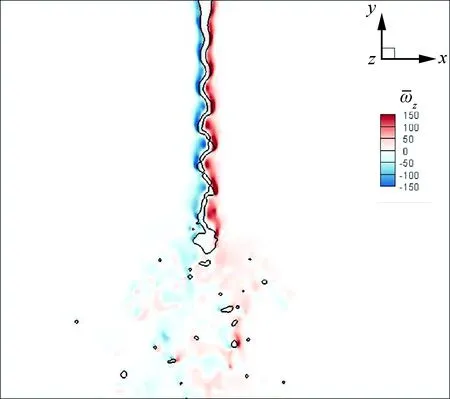
图14 液膜破碎区域涡量分量的分布云图Fig.14 Contour of vortex component of liquid sheet breakup region

数值模拟统计液滴粒径的方法是由液滴的体积进行换算，由包含在气液界面内的网格体积与网格内液相体积分数相乘求和得到液滴的体积，假定液滴形状为球形，由球形的体积计算公式计算得到液滴的直径。统计不同网格分辨率条件下雾场液滴尺寸分布的概率密度函数(Probability Density Function, PDF)，其定义为某个粒径区间内的液滴概率，不同网格分辨率的液滴粒径统计结果如图15所示。当网格加密等级较低时，数值模拟会捕捉到一些大尺寸液滴。随着网格分辨率的提高，数值模拟捕捉到的液滴尺寸开始向小粒径区域偏移。需要指出的是，当网格分辨率不够时，就会发生数值破碎而产生伪液滴，这种情况会随着网格分辨率的提高而得到改善，但是并不能够完全消除。如果非线性不稳定也能产生飞溅的小液滴的话，由于网格分辨率的缺陷也会导致对这种小液滴捕捉不够准确，因此需要对这种小液滴进行剔除。数值模拟的有效性应体现在可以较为完整地展现整个雾化过程，并且数值破碎产生的小液滴所占的比例足够小。假定小于4个网格捕捉到的液滴属于伪液滴，使用Gerris自带的RemoveDroplets函数将小于4个网格捕捉到的液滴全部剔除，因此统计曲线的起始点并不是零点。由图15可以看出，计算得到的液滴粒径分布范围大致在0～350 μm，液滴粒径概率密度分布的峰值在50～200 μm之间，概率密度数值基本在0.02以上。

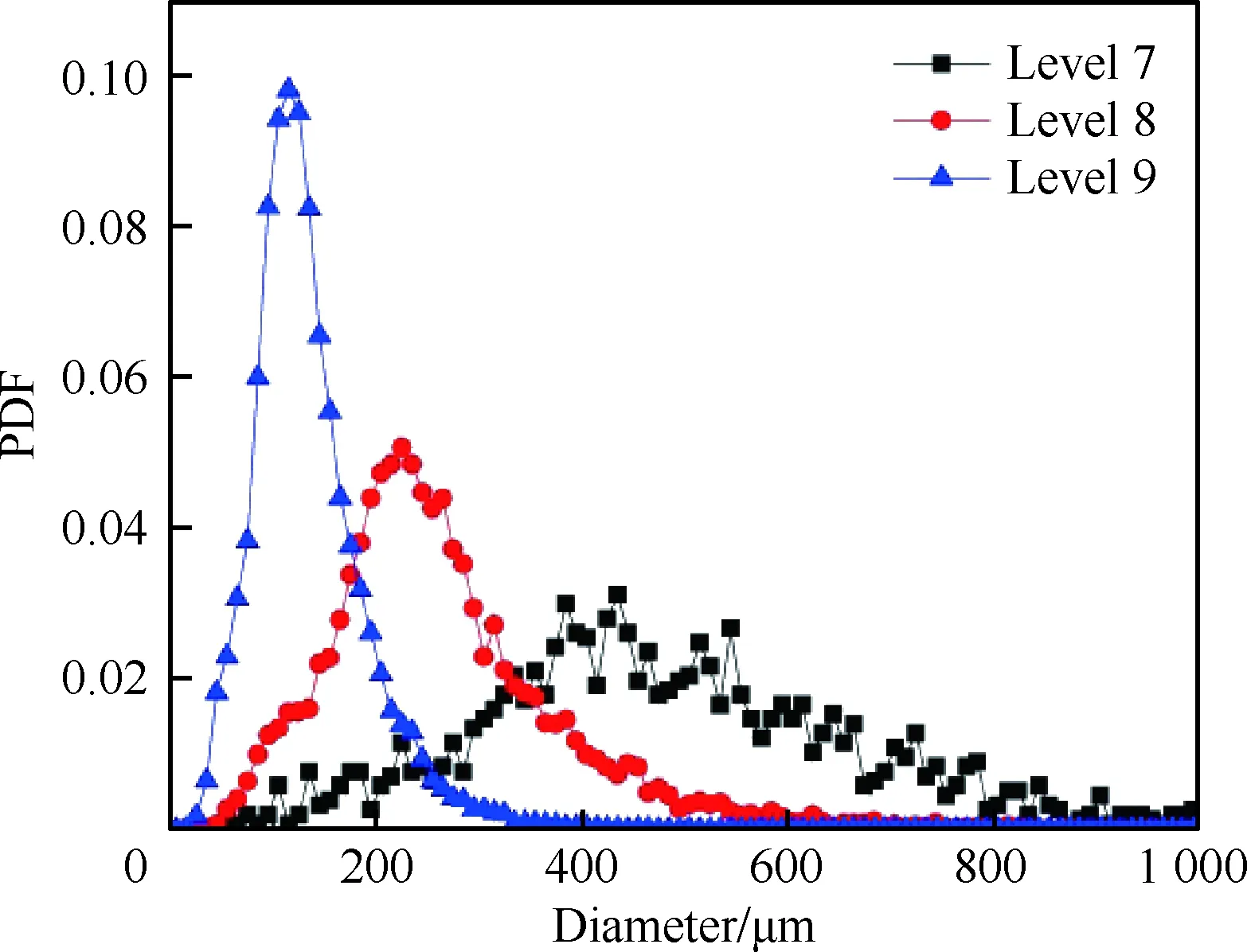
图15 不同网格分辨率的液滴尺寸分布Fig.15 Droplet diameter distributions of different mesh resolutions

3 结果分析

3.1 强迫扰动下的射流撞击雾化特性

在前面已经提到，背压振荡与喷前压力扰动都会引起喷射速度的周期性变化，二者在幅值与相位上存在一定关系，可以通过开展喷前压力扰动试验，并结合系统动力学分析将喷前压力扰动转化为背压振荡对喷射的影响。采用水力扰动装置产生喷前压力的扰动，开展了前端扰动条件下的射流撞击雾化试验，试验采用孔径为1 mm的喷嘴。首先对比强迫扰动雾化与自然雾化之间的差别，然后着重探讨强迫扰动条件下的撞击雾化特性。图16为脉动压力传感器记录得到的典型喷前脉动压力p′，水力扰动装置迫使喷前压力出现周期性振荡，从而使喷注压降发生周期性改变，最终导致喷射速度周期性变化，并调制出雾化的Klystron效应。对该脉动压力信号作快速傅里叶变换(FFT)，可以得到该脉动压力的频谱图，如图17所示，脉动压力的频率为1 782 Hz。由高速摄影对存在喷前压力扰动与不存在喷前扰动的喷雾场分别进行拍摄，图18(a)为不存在扰动时的自然雾化图像，图18(b)为存在喷前压力扰动的雾化图像。从宏观上看，二液滴空间分布比较均匀，而对于存在扰动时的喷雾场，在液膜下游则出现了大量液滴群聚集的弓形结构，观察不同时刻的高速摄影图像可以发现弓形液滴群的出现表现出一定的周期性。Rayleigh准则[48]指出了发生燃烧不稳定的2个必要条件：① 存在周期性的释热波动；② 压力振荡与释热波动同相位。当同时满足这2个条件时，压力振荡就会在正反馈机制下持续放大。雾化的周期性必然导致周期性的燃烧释热，如果周期性的燃烧释热与周期性的压力振荡耦合在一起形成正反馈，则有可能调制出燃烧不稳定，由此可以推断，背压振荡调制出的周期性雾化有可能成为燃烧不稳定的驱动机制之一。

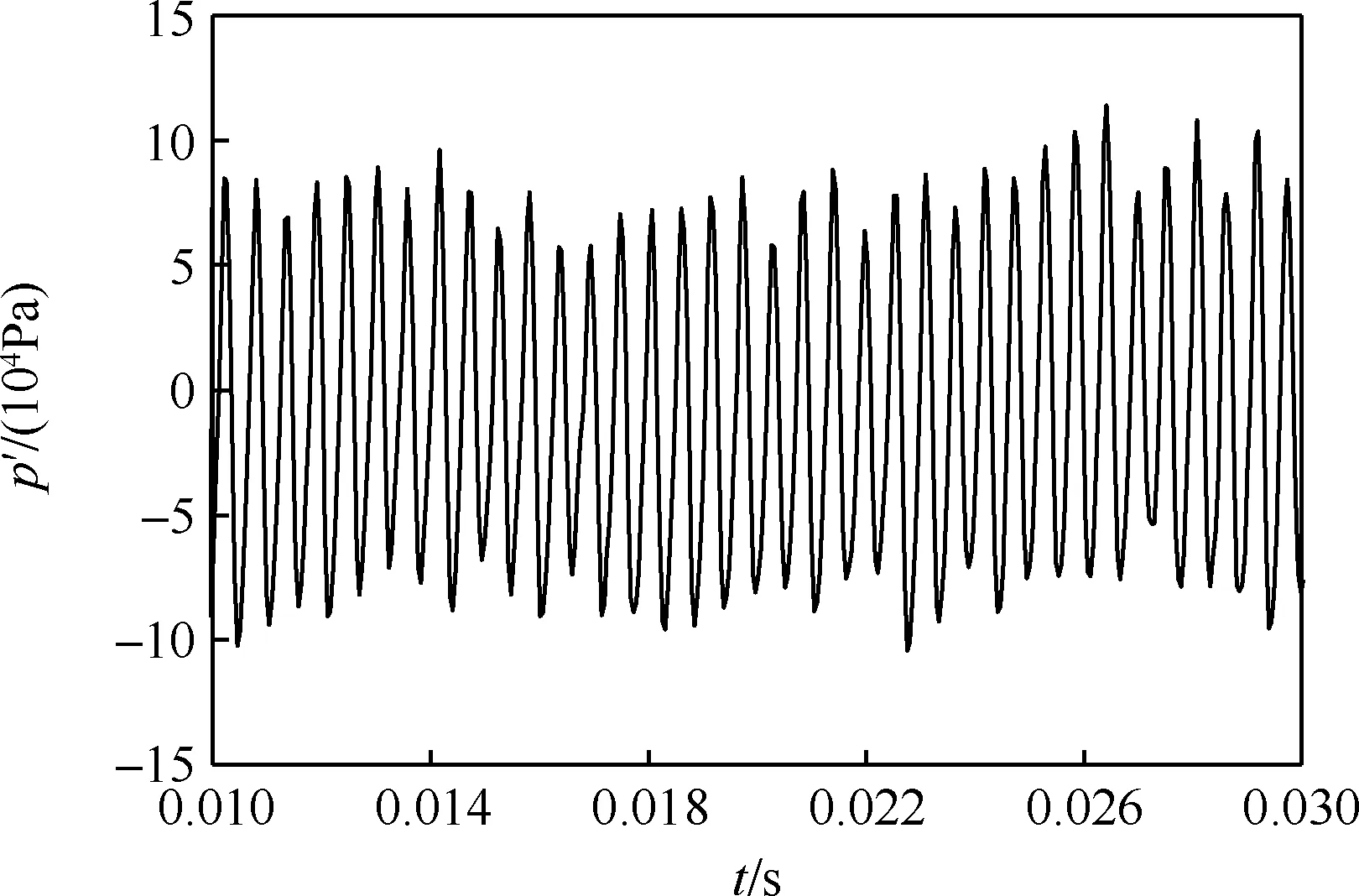
图16 喷前脉动压力Fig.16 Pulsating pressures before injection

图17 脉动压力的频谱分布Fig.17 Spectral distribution of pressure fluctuations

图18 撞击式喷嘴的喷雾场Fig.18 Atomization field of impinging liquid jets

(15)

为获得更多的数据信息，本文基于开源程序Gerris开展了数值模拟，重点关注的是喷射速度的周期性变化对于雾化特性的影响，因此，模拟强迫扰动雾化的方法是按照式(14)在边界给定随时间周期性变化的喷射速度。设定射流的平均速度u0=31.5 m/s，速度的扰动幅值u′=0.05，扰动频率f=1 782 Hz，其他结构参数与试验所用的喷嘴参数一致。数值计算得到的自然喷雾场与强迫扰动下的喷雾场对比如图22所示，二者之间的差别与试验观察到的雾场区别一致，自然喷雾场的液滴空间分布比较均匀，而强迫扰动下的液膜下游出现了大尺度的弓形结构，并且在雾场出现了局部液滴聚集的周期性现象。在一个周期T内，雾场随时间的变化如图23所示，由一个周期内的雾化过程可以对撞击雾化的Klystron效应形成机制进行阐述。当喷射速度出现周期性变化时，运动速度较快的流体追击运动速度较慢的流体，在射流中出现“鼓包”的现象，如图23(a)，之后“鼓包”向下游运动并在撞击点位置相互撞击，如图23(d)。该现象类似于射流速度更高、直径更大的两束射流撞击，撞击之后的液膜厚度与宽度增加，如图23(e)。 液膜变得更加不稳定，大尺度的弓形液团形成并在液膜下游脱落，如图23(f)～图23 (h)。液团在向下游运动过程中快速破碎并形成大量在空间聚集的液滴群，整个物理过程在时间上表现出显著的周期性特征，类似于射流的Klystron效应，可以认为是撞击雾化表现出的Klystron效应。

图19 3个观察窗的大小与位置Fig.19 Positions and sizes of three interrogation windows

图20 自然雾化随时间变化的灰度值与相应的FFT结果Fig.20 Time varying grayscale values and corresponding FFT results for natural atomization

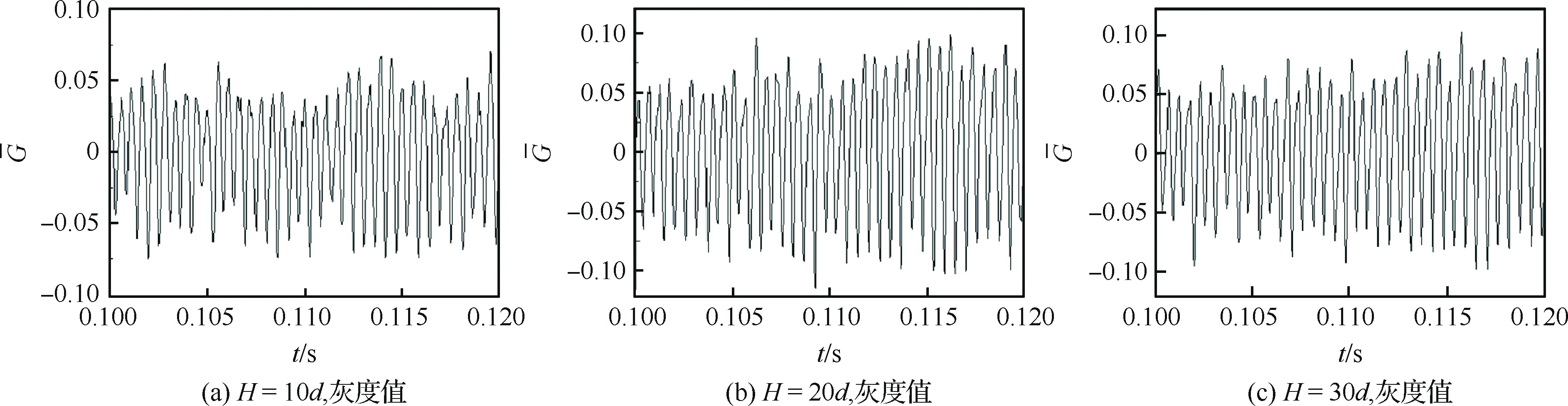
图21 强迫扰动雾化随时间变化的灰度值与相应的FFT结果Fig.21 Time varying grayscale values and corresponding FFT results for atomization with forced perturbations

图22 数值模拟得到的不同喷雾场的对比Fig.22 Comparison of different atomization fields from numerical simulations

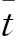
图24 不同位置处速度分量随时间的变化Fig.24 Time varying velocity component at different positions

与试验统计雾场信息的方法类似，在撞击点下游某个位置处设定观察窗，统计该区域的液滴信息。统计撞击点下游10d与20d位置处，厚度为2d，宽度为30d区域内的液滴数目以及Sauter平均直径(SMD)随时间的变化。自然雾化的液滴信息统计结果如图25所示，可以看出液滴数目以及Sauter平均直径的变化与试验观测的灰度信息类似，呈现出随时间无规律变化的特征。而当喷射速度周期性变化时，观察窗内的液滴数目以及液滴的Sauter平均直径则表现出周期性变化的特征，如图26所示，并且周期性波动的频率与施加的强迫扰动的频率一致。对某个时刻两个观察窗内的液滴粒径分布进行统计，统计结果分别如图27(a)和图27(b)所示。当存在强迫扰动时，小尺寸液滴所占的比例提高，大尺寸液滴所占的比例减小，表明在强迫扰动的作用下，观察窗内的液滴平均尺寸有减小的趋势。对一段时间内观察窗内的液滴数目与液滴粒径进行时间平均，统计结果如表1所示。当存在周期性扰动时，观察窗内的液滴数目显著增多，时间平均之后的Sauter平均直径显著减小，最大Sauter平均直径也相应减小。与自然雾化相比，强迫扰动雾化的2个观察窗内液滴数目分别提高了6.0%与13.3%， 时间平均的Sauter平均直径分别减小了8.8%与5.5%。由数值模拟结果可以看出，当存在前端扰动时，雾场空间局部区域生成的液滴数目显著增多，并且液滴粒径有减小的趋势。由Qin等[7]的研究成果可以得知，燃烧不稳定的激发与液滴粒径有强的相关关系，液滴粒径的减小与液滴数目的增多更有利于激发燃烧不稳定，强迫扰动下的雾化有可能成为燃烧不稳定激发的重要中间环节。

图25 自然雾化观察窗内的液滴数与SMD随时间的变化Fig.25 Time varying droplet number and SMD of interrogation windows of natural atomization field

图26 强迫扰动雾化观察窗内的液滴数与SMD随时间的变化Fig.26 Time varying droplet number and SMD of interrogation window of atomization field coupled with forced perturbations

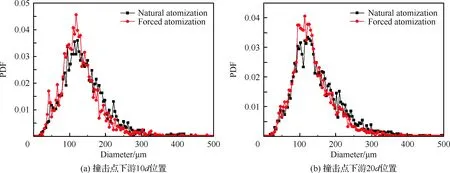
图27 观察窗内的液滴粒径分布Fig.27 Droplet diameter distribution in interrogation windows

表1 自然雾化与强迫扰动雾化观察窗内的液滴粒径信息Table 1 Droplet information of two interrogation windows of natural atomization and forced atomization

3.2 扰动频率对雾化特性的影响

这一部分将分析扰动频率对于撞击雾化的影响，通过改变电机转速实现对频率的调节，图28给出了不同频率的喷前脉动压力作快速傅里叶变换之后的频谱图，扰动的频率从1 347 Hz一直变化到3 563 Hz。图29为对应的不同扰动频率条件下的雾场图像，从图29可以看出在所研究的频率范围(1 347～3 563 Hz)内，撞击式喷嘴的雾化对扰动都存在响应，在强迫扰动的作用下撞击雾场都表现出周期性特征，表明撞击式喷嘴的雾化在一个非常宽的频带范围内对扰动都存在响应。这也表明撞击式喷嘴的工作状态易受到外界的影响，并不是一种工作特别稳定的喷注雾化单元，这种结构形式的喷嘴非常容易产生燃烧不稳定[20]。

图28 不同脉动压力的频谱分布Fig.28 Spectral distribution of different pressure fluctuations

从宏观上看，随着扰动频率的增大，空间局部聚集的弓形液滴群之间的间距在减小，表明液膜下游弓形液丝脱落的频率也在提高，与强迫扰动的频率变化保持一致。

图29 不同频率下的强迫扰动喷雾场Fig.29 Forced atomization field with different pressure fluctuation frequencies

图30 同步测量的灰度与脉动压力信号Fig.30 Synchronous signals of grayscale values and fluctuating pressures

(16)

图31 压力振荡与非稳态释热之间的时滞Fig.31 Time delay between pressure fluctuations and unsteady heat release

假定相邻2个脉动压力波形之间的相位差为360°，统计得到的不同频率条件下雾场灰度与脉动压力之间的相位差如图32所示。从图中可以看出扰动频率对相位差影响很大，雾场相同位置处，扰动频率越高，灰度信息与扰动压力之间的相位差值也就越大。在相同的距离范围内，扰动频率越高，统计得到的相位差的变化区间也就越大，表明在相同的距离内所包含的灰度变化周期更多，这也与从图29中观察到的弓形液滴群之间距离减小的现象一致。文中得到的是喷前脉动压力与雾场灰度之间的相位关系，通过系统动力学分析可以得到产生相同流量脉动的条件下，后端扰动与前端扰动之间的相位关系，这样就可以间接得到后端压力扰动与脉动灰度之间的相位关系，考虑其他子过程之后由图31可以得到最终的相位关系。未来可进一步考虑燃烧的影响，建立起基于周期性雾化的燃烧稳定性分析理论体系。

图32 不同频率灰度值与振荡压力之间的相位角Fig.32 Phase angle between grayscale values and pressure fluctuations at different frequencies

3.3 扰动幅值对雾化特性的影响

液体火箭发动机推力室内的室压通常都存在小幅值的波动，只有当发生燃烧不稳定时，扰动压力的幅值才会超出稳态室压的10%以上，扰动压力的幅值是甄别燃烧不稳定是否发生的一个重要参数，这一部分将采用数值模拟的方法研究扰动幅值对撞击雾化的影响。当推力室内出现纵向振荡时，喷嘴处于压力波腹的位置，反压振荡影响雾化的主要作用机制是通过改变喷注压降继而改变喷射速度，从而对雾化产生影响，也就是本文所研究的作用机制。选取与某型推力室一阶纵向不稳定频率接近的频率作为参照频率来研究扰动幅值对于撞击雾化的影响。根据式(14)，设定扰动频率为2 230 Hz，扰动幅值的大小u′依次为0.01，0.05，0.1，0.2与0.5，计算得到不同扰动幅值条件下的喷雾场分别如图33所示。由图33(a)可以看出，当扰动幅值很小时，雾场空间并没有形成局部聚集的液滴群，强迫扰动的喷雾场与自然喷雾场相比并没有显著差别，可以认为喷嘴此时工作在准稳态条件下。只有当扰动幅值高于某一临界值之后，雾场才会发生显著改变。由图33(b)～图33(e)可以看出，随着扰动幅值的增大，振荡压力场对于雾化的影响加剧，空间局部聚集的液滴群更加明显，并且液膜的变形更加剧烈。图34为不同扰动幅值条件下，雾场XY截面体积分数分布灰度图。从图中可以看出，扰动幅值的大小对于撞击前射流的状态影响较大。扰动幅值增大，射流中液体堆积形成的“鼓包”更加明显，表明雾场的Klystron效应更加显著。并且扰动幅值对于射流撞击之后的液膜波动状态、液膜的厚度分布以及破碎长度都有影响，液膜的破碎机制也发生变化，破碎过程由撞击波主导开始转变为撞击波与Klystron效应共同主导。

图33 不同扰动幅值下的强迫扰动喷雾场Fig.33 Forced atomization field with different perturbation amplitudes

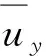
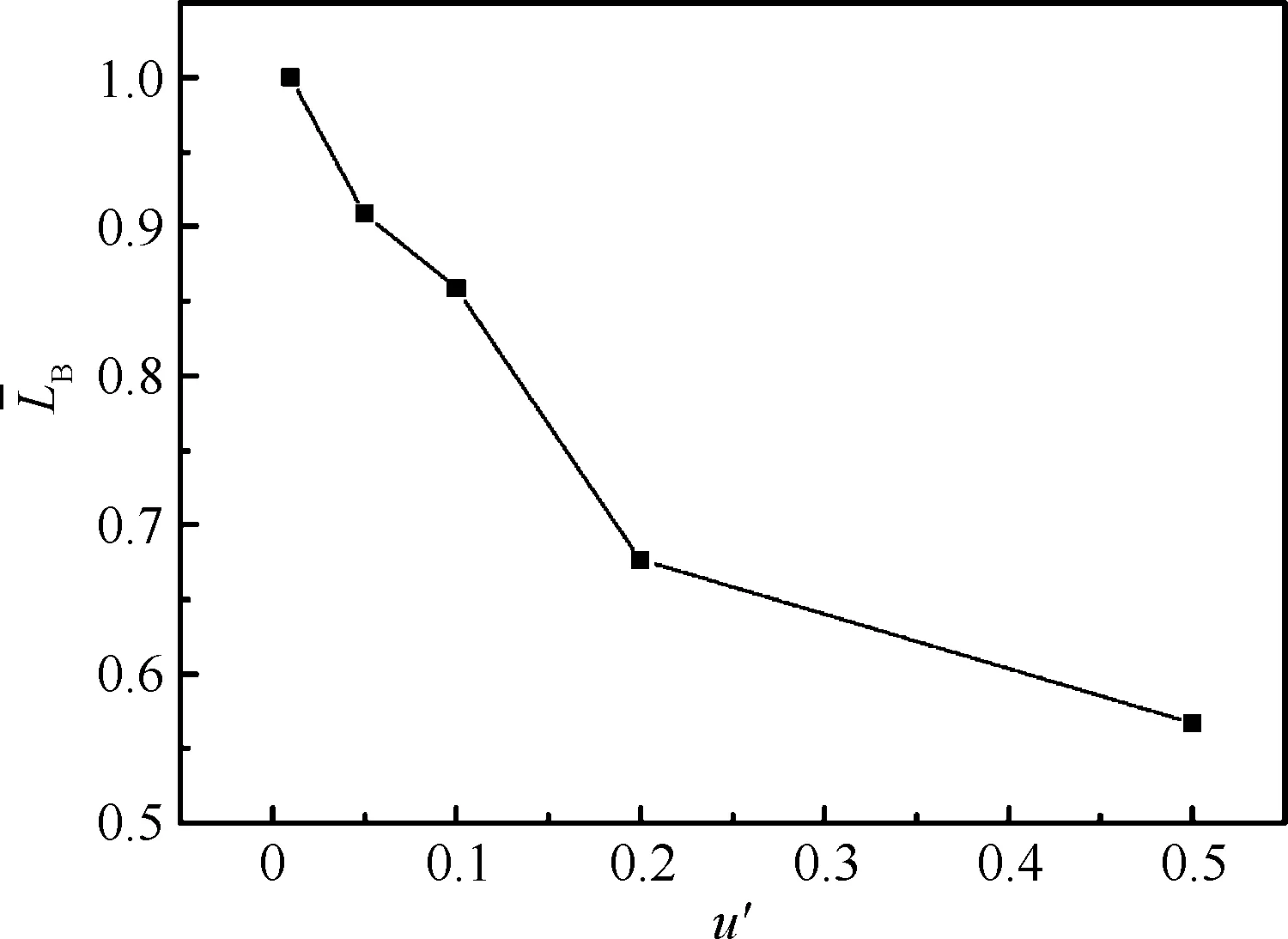
图35 不同扰动幅值下液膜的无量纲破碎长度Fig.35 Dimensionless breakup lengths of liquid sheet with different perturbation amplitudes

图36 不同扰动幅值下撞击点下游3d位置的速度分量Fig.36 Velocity component on point 3d downstream impingement point with different perturbation amplitudes

4 结 论

燃烧不稳定的显著特征是推力室内周期性的背压振荡，背压振荡会引起喷射速度的周期性变化，从而调制出与自然雾化显著不同的雾化特性。本文采用数值模拟结合试验的方法研究了强迫扰动条件下的射流撞击雾化特性，主要目的就是全面把握喷嘴的工作特性，进一步认识自然雾化与强迫扰动雾化之间的差别以及雾化在燃烧不稳定中所起的作用，得出的主要结论如下：

1)基于树形自适应网格与分段线性的VOF方法建立的雾化数值模拟方案可以细致刻画出强迫扰动条件下的撞击雾化过程，模拟得到了强迫扰动作用下的周期性喷雾场，可以为燃烧不稳定正反馈机制的研究提供重要的参考，并为非稳态燃烧的数值模拟提供准确的初边值条件。

2)强迫扰动的喷雾场与自然喷雾场之间存在显著差别，自然喷雾场的液滴在空间分布比较均匀，强迫扰动条件下的射流撞击喷雾场出现了弓形液滴群局部聚集的现象，并且在时间上表现出周期性特征，雾化频率与强迫扰动的频率一致。在本文研究的频率范围(1 257～3 563 Hz)内，撞击式喷嘴的雾化对扰动都有响应，表明撞击式喷嘴的雾化在一个非常宽的频带范围内对扰动都存在响应。

3)扰动频率主要影响雾场空间相邻弓形液滴群之间的间距，以及雾场与振荡压力场之间的相位关系。扰动频率越高，雾场空间某一固定位置与扰动压力之间的相位差越大，并且在相同的距离范围内，相位差的变化区间范围也越大。

4)扰动幅值决定了雾化Klystron效应的强度，只有当扰动幅值高于某一临界值时，雾场才会表现出周期性特征。扰动幅值增大，液膜的破碎长度减小，撞击点下游的流量波形由正弦波向陡峭前缘波转变，表明流量由线性变化向非线性变化转变。

5)强迫扰动下喷雾场的许多特性都更加有利于激发燃烧不稳定，比如雾场表现出的周期性特征，雾场出现局部聚集的液滴群，以及流量特性由线性向非线性的转变等等，这些特性的出现有可能在正反馈机制中起到推波助澜的作用，需要在非稳态雾化的基础上开展燃烧的研究来进一步明确这些特征对燃烧特性的影响。

下一步工作：采用光学手段直接测量喷嘴出口周期性变化喷射速度，为数值模拟提供更加准确的边界条件；进一步测量雾场的微观信息，采用微距镜头结合图像处理获得瞬态液滴粒径随时间的变化规律；在雾化研究的基础上进一步建立燃烧响应模型，从而构建起基于周期性雾化的燃烧不稳定分析理论体系。

致 谢

本项工作在国家超级计算天津中心的“天河一号”超级计算机上完成，感谢天津超算中心的大力支持。