非均匀来流下三维激波反问题的微元密切轴对称解法
2020-12-28周航金志光
周航,金志光
南京航空航天大学 能源与动力学院, 南京 210016
在过去的几十年间,高超声速技术取得了极大进步,并不断推动着高超声速飞行器研究研制工作的变革与发展[1-2],高超声速飞行器前体、进气道及二者的气动一体化设计是其中的重要研究方向[3-6]。
乘波体因其显著的高升阻比和高效预压缩特性,长期以来被公认是高超声速飞行器设计领域的一种理想构型[7-8]。乘波理论中,前缘激波与飞行器边缘在精心设计下能够完美贴合,飞行器犹如“乘坐”在激波面之上,故而得名。在利用乘波概念进行高超声速飞行器前体、进气道设计时,一般首先需要进行无黏基准流场构建,其中关键在于对前缘激波的设计和控制,然后从激波面上选定的前缘线进行流线追踪[9],即可得到具备乘波特性的气动压缩面。在乘波设计理念的指导下,很自然地逐渐发展形成了两种设计思路:① 给定激波生成体,通过数值计算得到激波面和波后流场;② 给定激波形状,通过求解反问题得到压缩面和波后流场。
第1类设计思路中,研究者首先基于楔、锥形流的理论解展开设计,例如分别由Nonweiler[10]和Jones等[11]提出的“Λ”构型乘波体和锥导乘波体。Rasmussen[12]应用高超声速小扰动理论基于小攻角圆锥绕流和椭圆锥绕流设计了乘波体构型。随着CFD技术的发展,更多更加复杂的流场被用作乘波体基准流场,通过直接求解三维欧拉方程,Takashima和Lewis[13]研究了楔锥混合乘波体,Cui等[14]基于方锥、花锥、十字锥绕流研究了广义锥导乘波体。
第2类设计思路起始于Sobieczky等[15-17]提出的密切轴对称(Osculating Axisymemtric flow,OA)理论及横向推进求解(Cross-Stream Marching,CSM)方法,其能够基于广义激波形状进行乘波体构型设计。自该理论提出后,直到今天仍引领着密切锥乘波体的研究热潮,有关该理论的修正[18-19]、发展[20-23]和应用[24-28]工作层出不穷。其中包括,Chauffour和Lewis[18]与Rodi等[19]先后针对密切锥乘波体设计中的横向压力梯度与横向流动进行的修正;Qiao等[20]发展的CSM方法,其给出了一种精确性和鲁棒性得到提升的CSMP方法;Zheng等[21]拓展并提出的多密切锥方法(Mutiple-OCs),通过在密切面内的非共轴特征线(Noncoaxical Method of Characteristics)计算,使得沿激波面周向不同位置可以有不同的激波强度;Chen等[22]通过调整横截面激波曲率中心位置,给出的高容积率密切锥乘波体设计方法;Liu等[23]基于各密切面上不同的来流马赫数设计的宽速域密切乘波体。
事实上,两种思路均能得到满足要求的基准流场,但各有长短。前者在设计时能够得到更多复杂构型下的超声速基准流场,无需拘泥于采用二维平面激波、二维轴对称激波等简单几何形状,但其生成的激波可控性较差。后者作为一种反向设计,能够对所乘激波形状进行精细控制,但实现难度较大,尤其是三维情况下,现阶段仅在某些特殊限制内(如激波形状为三维密切轴对称曲面,来流条件为均匀水平气流等)实现了对曲面激波反问题的求解,而一般意义上的三维曲面激波反设计问题目前仍处于探索阶段[20-21,29]。工程中,高超声速飞行器的前体、进气道设计往往存在各种限制条件,导致两者的气动一体化设计难度较大,灵活性亟需进一步提高,有必要发展更多针对该问题的求解方法。
本文首先在传统密切轴对称方法基础上,探讨了针对非均匀来流条件的三维曲面激波设计反问题,然后提出了一种针对该问题的微元密切轴对称解法(Micro Osculating Axisymmetric flows,MOA)。为验证求解方法和相关程序的正确性和可行性,采用该方法重构了一个4°攻角条件下的内锥激波生成体,和一个10°外锥形流中的内锥激波生成体,并分别与CFD数值仿真结果进行了对比。最后讨论了该方法在前体/进气道一体化设计中的应用前景。
1 传统密切轴对称方法
20世纪90年代,Sobieczky等证明了空间三维流动可以用密切平面内的轴对称二维流动等效[15],进而由此提出了密切轴对称理论,解决了三维密切曲面激波的反设计问题。
图1以内锥形激波为例,阐释了传统密切轴对称理论的基本原理。沿着非轴对称内锥激波周向,三维空间被离散为一系列二维切片,即密切平面,这些周向排列的密切平面与激波曲面垂直,与波前来流平行。同时,三维内锥激波及波后三维流动亦被视作这些密切平面上轴对称二维激波和二维流动的叠加,而根据轴对称二维激波曲线反设计压缩面型线可借助二维逆特征线法实现。
为避免各密切平面之间横向流动的干扰,每个密切平面内轴对称二维流动的激波曲线形状均相同,即激波强度相同,从而保证了各密切平面内的激波后沿压力相等,这也是上文所述用轴对称二维流动等效空间三维流动的前提。
各密切平面上轴对称流动的唯一区别在于其对称轴位置各不相同(如OAOA′,OBOB′等),它们由基准横截面上激波曲线的局部曲率中心位置决定。实际上,这也正是密切轴对称流动与轴对称流动的差别所在:密切轴对称流动是一种更为广义的轴对称流动,后者只是前者在横截面上激波曲线形状为圆形时的一种特例,此时,各密切平面即为相同的轴对称平面,各局部曲率半径即为同一个圆弧半径,各局部曲率中心即为同一个圆弧中心(见图2)。
根据传统密切轴对称理论基本原理可知,只有当各密切平面之间不存在横向速度与横向压力梯度时,这种采用周向布置二维密切平面组成三维空间的构造方法才是精确的。这说明密切轴对称理论仍然存在一定的局限性,其构造的三维激波只能是某种密切曲面,而非真正的任意三维曲面,并且只能基于均匀水平来流条件。

图1 传统密切轴对称理论示意图Fig.1 Schematic of traditional osculating axisymmetric flows concept
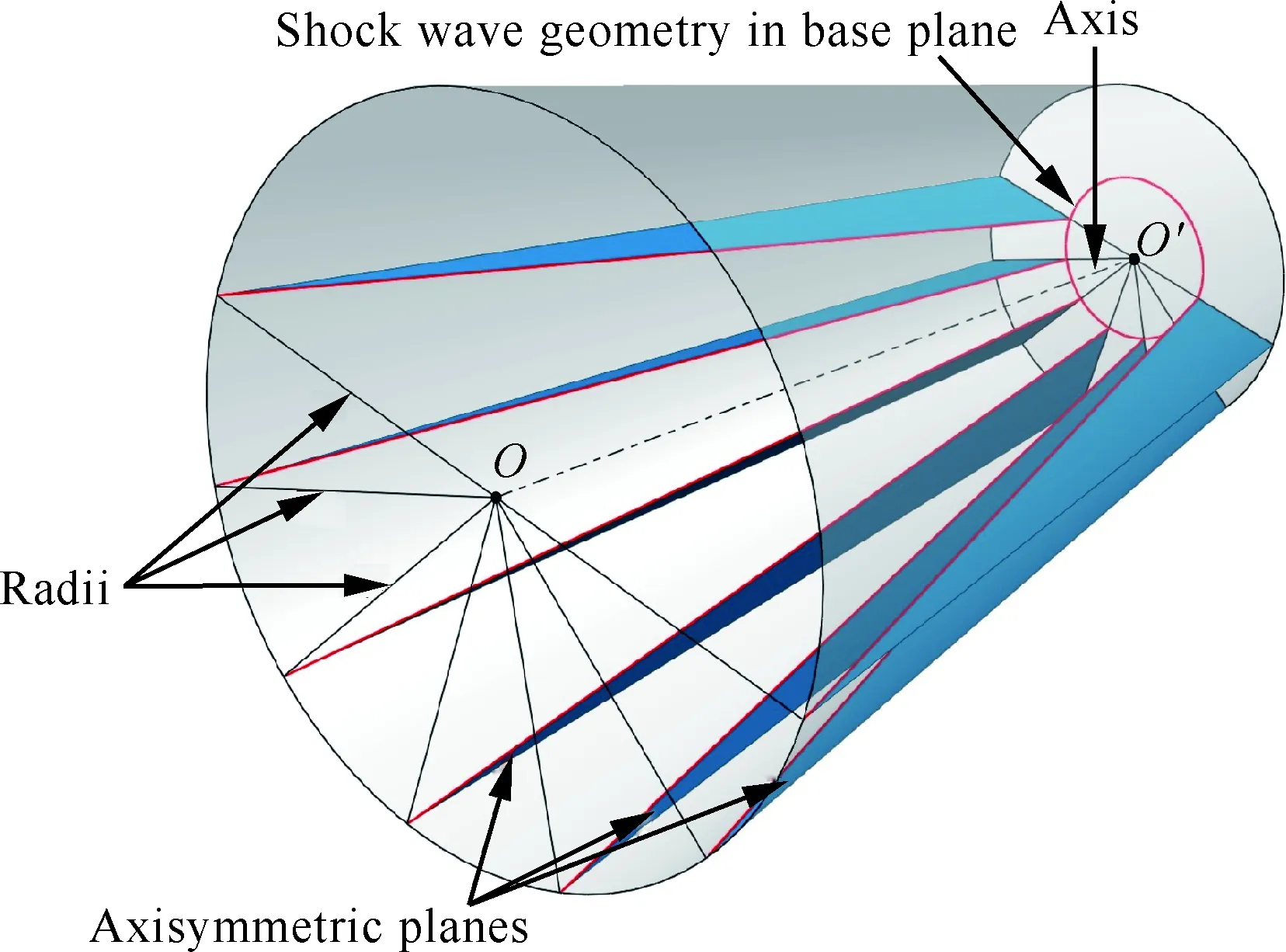
图2 轴对称内锥流动Fig.2 Axisymmetric internal conical flow
如图3所示,激波面为满足密切几何条件的内锥曲面,密切平面OABO′即xy平面,点P位于激波曲面与密切平面OABO′的交线上,P点波前速度矢量为
V=Vx+Vy+Vz
(1)
式中:Vx、Vy、Vz分别为x、y、z方向的速度矢量。
根据当地激波曲面形状和Rankine-Hugoniot方程,当波前为均匀水平来流时,Vy=Vz=0,波前速度V=Vx,波后速度方向仍在密切平面OABO′之内;而当波前为非均匀来流时,如Vz≠0,则波后速度必然存在垂直于密切平面OABO′的速度分量Vcross,若继续以密切面OABO′上的轴对称二维流动代替原空间三维流动显然是不合适的。这意味着传统密切轴对称理论中构造密切平
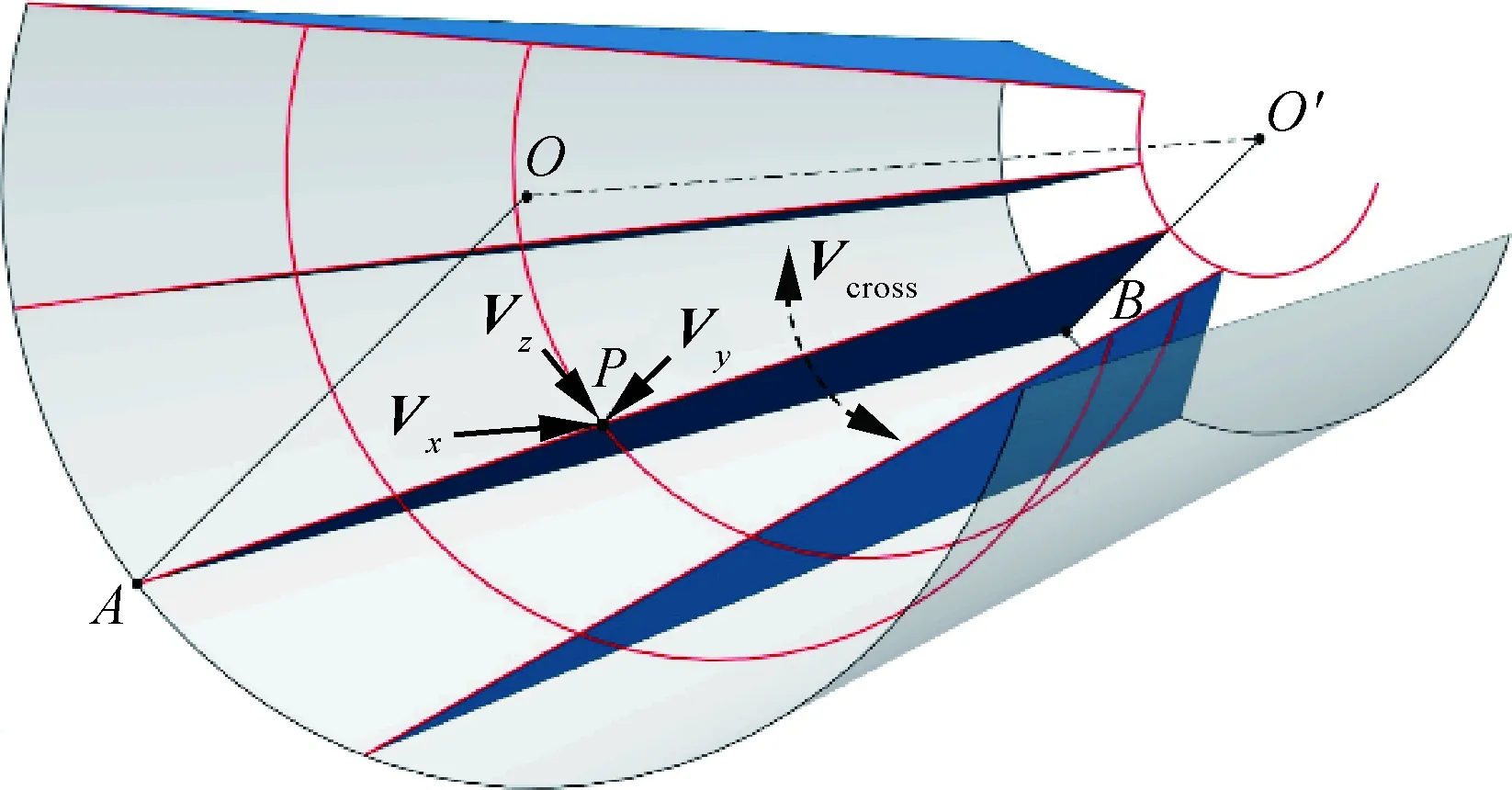
图3 传统密切轴对称理论适用性分析Fig.3 Applicability analysis of traditional osculating axisymmetric flows theory
面的方法失效,并且不难发现,在任意给定非均匀波前参数情况下,波后的三维流场中也不存在其他任何具备此前密切平面特征(例如无垂直方向上流动)的整张二维平面。
尽管如此,在三维激波曲面上的任意一点,仍能找到局部的微元密切平面,在该点附近的小范围内,依然能够延续用轴对称二维流动代替空间三维流动的等效求解思路。将该方法命名为微元密切轴对称方法,具体原理和实施方式在第2节进行详细分析。
2 微元密切轴对称方法
如图4所示,P11为激波面上一点,在非均匀来流下,其波前速度为某种任意指定大小和方向的Vpre,波后速度Vpost由当地激波曲面形状和Rankine-Hugoniot方程得到。本文所谓“微元密切面”(Micro Osculating Plane,MOP)之一即点P11附近由矢量Vpre和Vpost确定的微平面,由于Vpre方向的随机性,微元密切面并非传统密切理论中垂直于激波面的轴对称径向平面。
根据微元密切面定义,P点速度方向恰好在微元密切面之内,因此可以看作是一种局部的二维流动,在该点局部应用密切轴对称原理,即可将复杂三维流动转化为过该点的微元密切面上的轴对称二维流动进行求解。应当说明,在非均匀来流条件下,按照上述方法生成的激波面上各个局部微元密切面是以一种相对无序的方式排布的,即使是沿流向分布的一系列微元密切面(如图4中过点P11和点P12的微元平面),其上的轴对称二维流动也并非共用一根对称轴(如轴对称激波的对称轴OO′),而是各自拥有相互独立的“微元对称轴”(如图4中的O1O2和O2Oi)。微元对称轴的空间位置和角度各异,是由周向相邻两个微元密切面的交线决定的,这些特征与传统密切轴对称理论中整张密切平面对应整条对称轴不同。微元密切面与微元对称轴的确定是微元密切轴对称方法的关键。
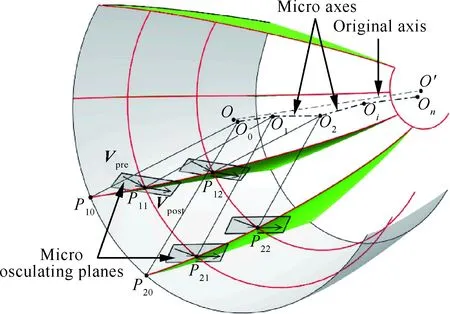
图4 微元密切轴对称方法示意图Fig.4 Schematic of micro osculating axisymmetric flows method
由于流场被离散为更多的微元密切面,而非传统密切理论中数个周向排布的密切平面,图5所示整张密切平面上的轴对称二维特征线法将难以直接应用,但在各个微元密切平面内,均为局部的轴对称二维流动,其控制方程依旧是连续性方程(式(2))、动量方程(式(3)~式(4))和声速方程(式(5)):
(2)
(3)
(4)
(5)
式中:ρ为密度;p为压力;Vx、Vy、Vz分别为x、y、z方向的分速度;c为声速。
特征线方法将这些偏微分方程转化为沿特征线的常微分方程,然后进行求解。式(6)~式(7)和式(8)~式(10)分别给出了特征线方程和沿特征线的相容关系[30]:
(6)
(7)
dp-c2dρ=0
(8)
pVdV+dp=0
(9)
(10)
式中:λ为特征线斜率;θ为流动角;μ为马赫角;V为速度;Ma为马赫数;下标0和±分别表示流线和左行/右行特征线。
值得注意的是,与在整张轴对称二维平面上进行推进求解不同,图5中前一条特征线的计算结果可以直接作为后续计算域的初值线(如P1Q1,P2Q2等),但在图6所示由一系列微元密切面拼接而成的三维扭转曲面上,则必须对各微元面内的数据进行处理,即把前一个微元密切面(Micro Osculating Plane,MOP)内结尾特征线(如MOP1内的P1Q1,MOP2内的P2Q2等)上的坐标与流动参数向后一个微元密切面当地二维坐标系内投影变换,从而保证特征线计算能够持续推进。这种处理有效避免了三维特征线计算,三维情况下,沿特征面的相容关系不再是常微分方程,问题将变得十分复杂,且有研究表明[31],与有限差分方法相比,三维特征线法在计算效率上也不再具备特殊优势。
最终,沿流向排布的一系列微元密切面组成一张三维流面,如图7所示,三维流动曲面相比二
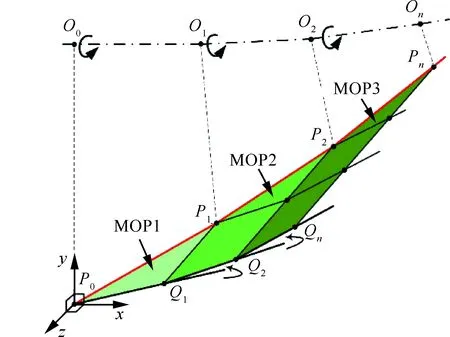
图6 流向排布微元密切面上的特征线网格Fig.6 Mesh of characteristic lines on curved micro osculating surface in flow direction
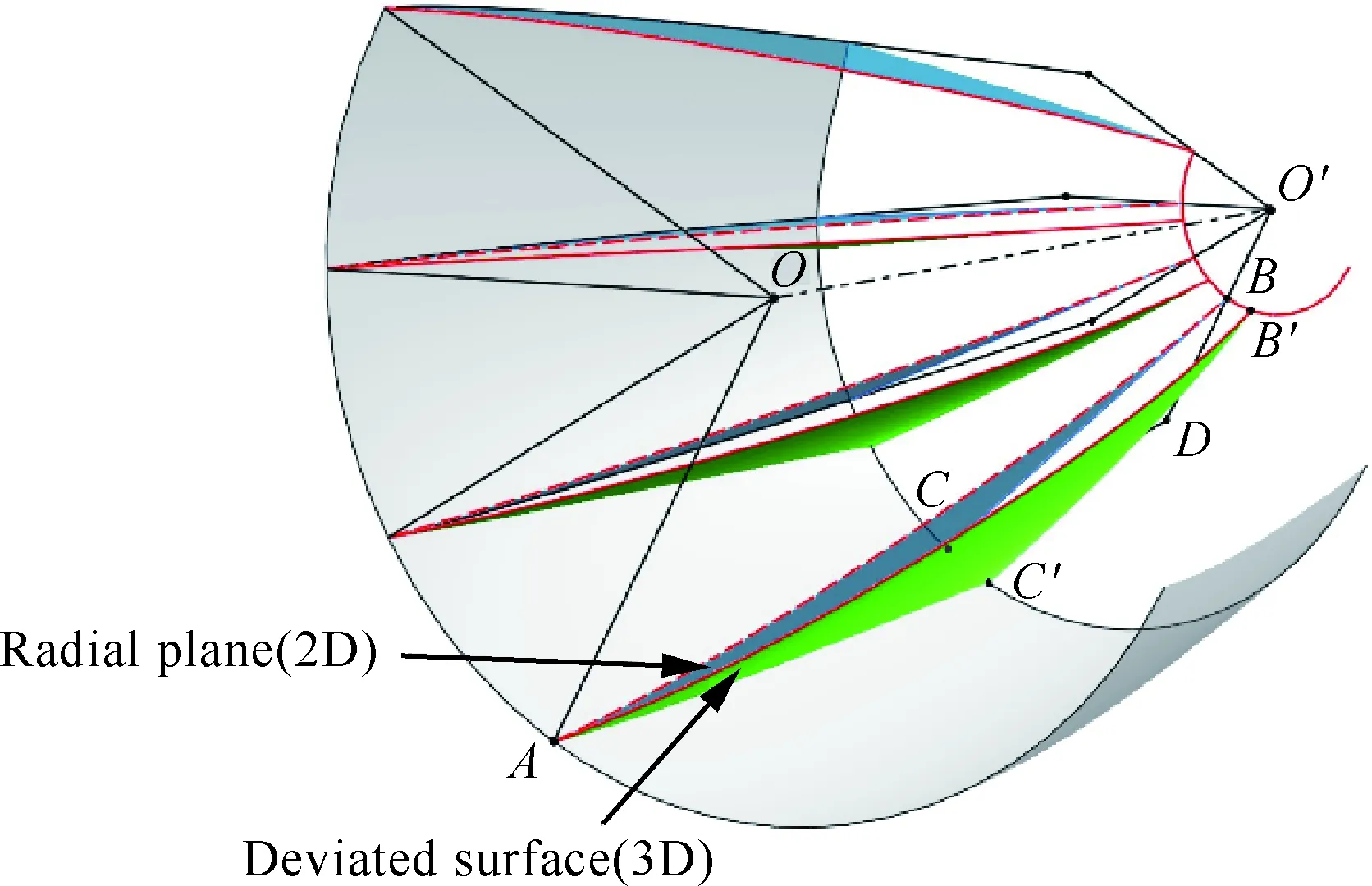
图7 三维密切曲面与传统二维密切平面对比Fig.7 Comparison of traditional 2D osculating plane and 3D surface consisting of micro osculating planes
维径向平面发生了明显的偏转,并且随着流动越向下游发展,偏离程度越大。
3 非均匀来流条件下三维曲面激波重构
基于上述方法编写了非均匀来流下三维曲面激波构建的设计程序,并以高超声速推进系统气动设计中的两类常见问题为例,分析讨论微元密切轴对称方法的设计结果,并与CFD数值仿真结果进行对比。三维定常流场的无黏数值仿真采用了ANSYS Fluent的密度基求解器,其中欧拉方程的求解采用有限体积法,无黏通量计算采用二阶AUSM (Advection Upstream Splitting Method)格式,气体性质选择为理想气体,比热比γ为1.4。计算过程的收敛依据为各项残差下降至少3个数量级并保持稳定。计算所用网格由ANSYS ICEM生成,由于对称性,仅取模型的一半进行网格划分,并在各压缩面前缘对激波根部区域进行局部加密,总网格量约350万。
3.1 带攻角来流下的内锥曲面激波反设计
高超声速飞行器常伴随着带攻角飞行,零攻角条件下设计得到的锥导乘波体构型在有攻角来流下,前缘激波将偏离设计位置,导致不能完全乘波。本节针对这一实际问题,采用微元密切轴对称方法,在来流马赫数Ma∞=6,攻角α=4°条件下根据预设的轴对称内锥曲面激波(对称轴水平)反设计了三维压缩面。
设计时指定的内锥激波母线形状如图8所示,曲线方程为
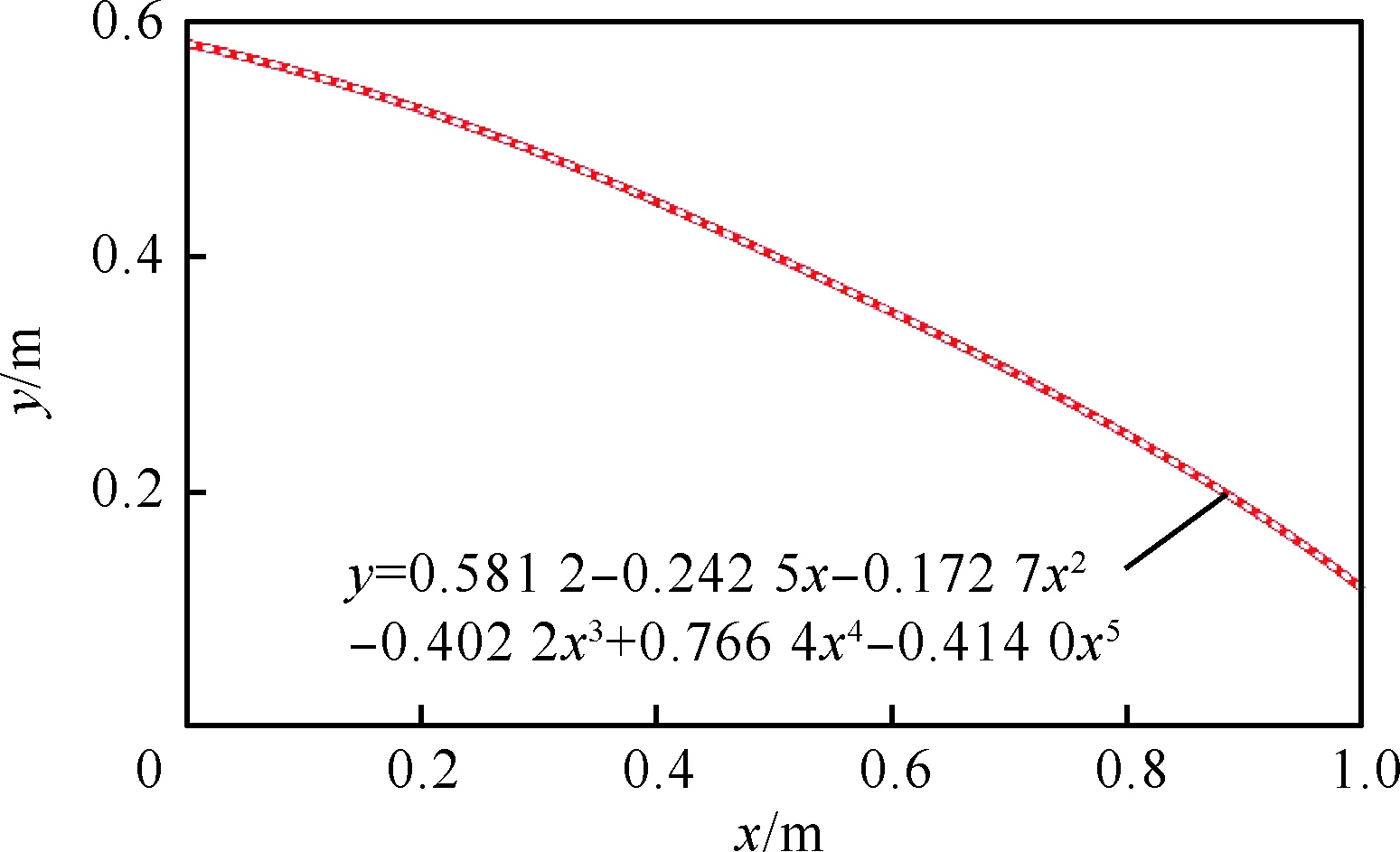
图8 内锥激波母线形状Fig.8 Internal conical shock wave geometry
y=A0+A1x+A2x2+A3x3+A4x4+A5x5
(11)
式中:A0、A1、A2、A3、A4、A5为系数,具体数值为A0=0.581 2,A1=-0.242 5,A2=-0.172 7,A3= -0.402 2,A4=0.766 4,A5=-0.414 0。
图9(a)给出了CFD计算得到的对称面流场,在4°攻角下,迎风侧与背风侧激波形状仍能保持完全相同,并与设计之初给定的激波形状(白色虚线)保持一致。图9(b)为横截面流场,图中V∞为来流速度,其中的激波形状亦保持为严格圆形。作为对照,图10考察了以均匀水平来流设计的压缩面在4°攻角下的表现,激波整体形状出现了明显的非轴对称性,横截面上的波后参数也呈现出更大的非均匀性,这些现象均对乘波体设计不利。值得注意的是,利用微元密切轴对称方法,尽管激波形状在攻角条件下能够被设计为标准内锥曲面,波后流场却并非为轴对称内锥流动,而是一种包含显著横向速度和参数梯度的三维流动。
为进一步衡量计算准确度,图11给出了两种方法得到的型面经CFD计算得到的激波位置与预设位置的误差曲线,其中Δh为实际激波位置与预设激波位置的纵坐标之差,R为进口半径。可以看出,传统二维方法由于未考虑波前来流的非均匀性,激波位置误差达到了6%,而MOA方法的误差最大约0.5%,准确度提升了一个数量级。另外,图12对比了采用微元密切轴对称方法和CFD计算得到的壁面压力曲线(图中p∞为来流压力),两者基本吻合,迎风侧与背风侧的最大误差分别为2.5%和4.3%。事实上,与其他数值解法类似,微元密切轴对称方法的计算精度与在激波曲面上选取微元密切面的数量有关,本例中沿流向和周向一共布置了25×19个微元密切面,随着离散程度的提升(计算量也会相应增加),计算误差还会进一步减小。
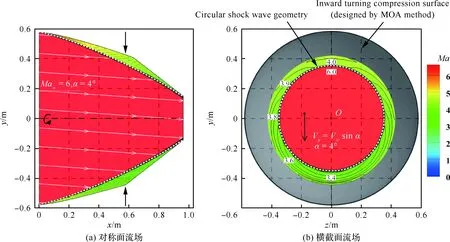
图9 利用MOA方法在攻角条件下生成的内锥激波的数值仿真验证Fig.9 Numerical validation of internal conical shock wave designed by MOA in incoming flow with angle of attack
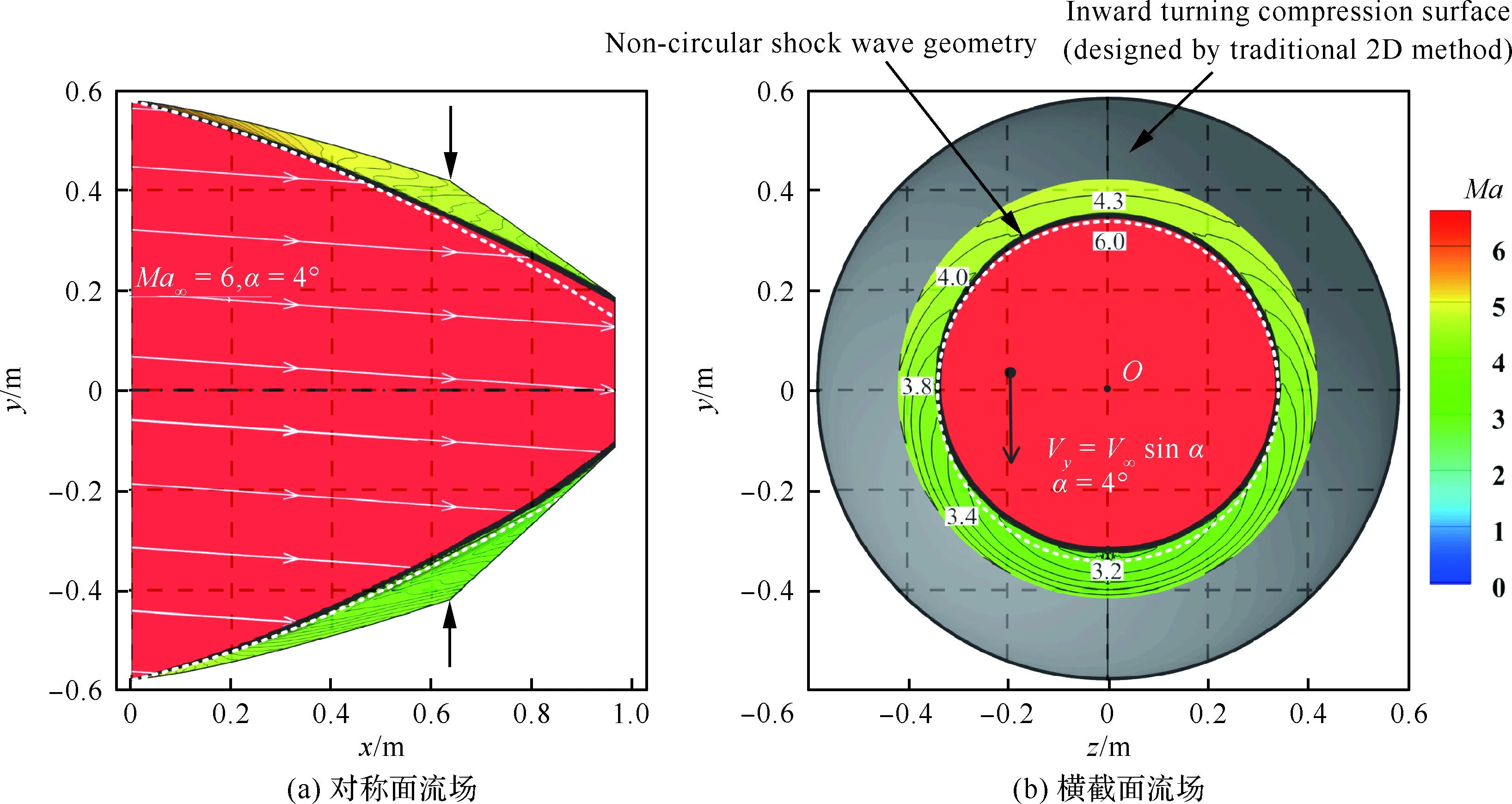
图10 轴对称压缩面在攻角条件下的流场Fig.10 Flowfield of axisymmetric compression wall in incoming flow with angle of attack
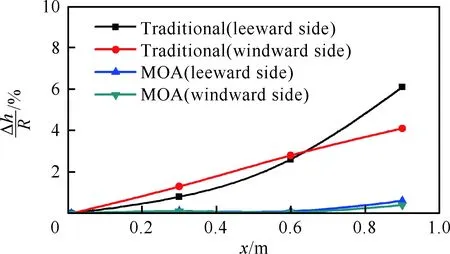
图11 流向激波位置的相对误差曲线Fig.11 Relative error curves of shock wave location along flow direction
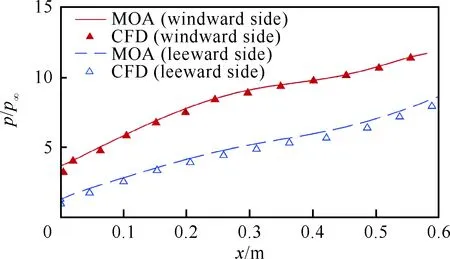
图12 MOA与CFD得到的壁面压力分布对比Fig.12 Comparison of MOA and CFD results of wall pressure distribution
3.2 外锥形流中的内锥激波反设计
在高超声速飞行器前体/进气道一体化设计时,进气道有时需被放置在经历了前体预压缩之后的流场内,这意味着进气道入口处气流不再是常规设计中的远前方均匀来流,因此必须考虑非均匀来流情况下的进气道设计。
基于外锥形流的乘波前体与基于内锥形流的内转进气道是现阶段的研究热点,图13给出了二者基准流场的一种耦合方式,其中,内锥激波曲面被包裹在外锥激波以内的部分激波面的波前参数由外锥流动决定。本节针对这种内外锥基准流场一体化构型,采用微元密切轴对称方法,在来流马赫数Ma∞=6、半锥角ψ=10°的外锥流场中根据轴对称内锥曲面激波反设计了三维压缩面。内锥激波母线形状仍由式(11)表达,其中系数更换为A0=7.600×10-1,A1=-6.653×10-1,A2=2.131× 10-1,A3=-2.281×10-1,A4=7.317×10-2,A5=-9.328×10-4。

图13 外锥与内锥流场的耦合设计示意图Fig.13 Schematic of integrated design of external and internal conical flows
设计结果如图14所示,其中包括用于产生所需非均匀外锥形流的前体锥面,和采用微元密切轴对称方法得到的内锥激波压缩面。在前体/进气道一体化设计中,进气道的唇口型线通常以横截面上的激波形状为基准,从而实现进气道的激波封口和全流量捕获,因此,横截面上的激波形状需要额外关注,图15在正视图视角下展示了所设计内锥激波形状在横截面上的准确度。由于2个基准流场不同心,前方外锥形流在内锥基准流场柱坐标系下具有明显的周向速度,即三维流动特征,但采用密切轴对称方法得到的内锥激波在横截面上的形状依旧保持为严格圆弧形(与标准圆弧虚线重合)。为进一步衡量其准确度,图16给出了各横截面上CFD计算得到的内锥激波位置与预设位置的误差曲线,其中横坐标θ为轴对称内锥激波的周向角度(对称面为0°),L为内锥激波流向总长度。在前方外锥激波的包裹区域内部,内锥激波各位置误差均不超过0.5%;当θ超出极限角度(内、外锥激波在横截面上的交点所处角度)后,由于内锥激波的波前流动参数不再是马赫数为6、10°半锥角的锥形流场参数,而是远前方均匀来流,即与设计时的输入条件不同,故激波形状开始出现显著偏差。
综上所述,采用本文所提出的微元密切轴对称方法针对2种非均匀来流重构的内锥激波形状均与数值仿真结果完全吻合,从而验证了本文微元密切轴对称方法的正确性与可行性。还应指出,应用图13所示内/外锥一体化基准流场,结合流线追踪技术,可以方便地设计出流向布局的三维乘波前体/内转进气道气动一体化构型:在内锥激波面上选取内转式进气道前缘线,然后分别在前方外锥流场与后方内锥流场中向前/向后流线追踪,即可得到相应的进气道壁面与乘波前体下表面。而在传统一体化方法中,由于内转式进气道(基准流场)基于均匀来流设计,须以平均流动参数代替非均匀的前体波后流场进行设计[32],或将内转进气道直接置于前体前缘捕获自由来流(此时前体位于进气道两侧,相当于周向布局的一体化构型)[33-34]。因此,采用基于非均匀来流下三维激波反设计方法得到的内外锥耦合流场,能够显著增强前体/进气道气动一体化设计的灵活性,相关工作值得进一步深入研究。
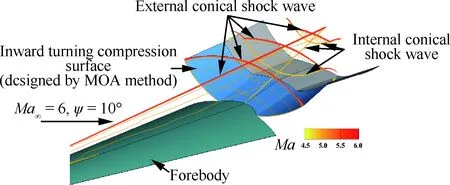
图14 内外锥耦合流场的数值仿真结果Fig.14 Numerical simulation results of integrated outward/inward turning flowfields
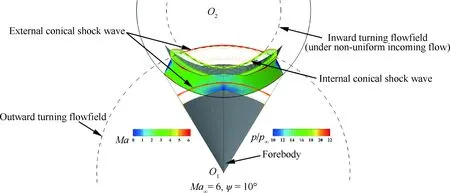
图15 利用MOA方法在外锥流场中生成的内锥激波的数值仿真验证Fig.15 Numerical validation of internal conical shock wave designed by MOA method in external conical incoming flow
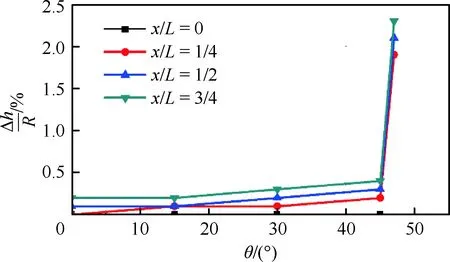
图16 周向激波位置的相对误差曲线Fig.16 Relative error curves of shock wave location along circumferential direction
4 结 论
本文讨论了针对非均匀来流条件的三维曲面激波反问题,提出了针对该问题的微元密切轴对称方法并进行了数值仿真验证。通过本文研究,得到以下结论:
1) 所提出的三维曲面激波反问题的微元密切轴对称方法,解除了传统密切方法中不能有横向流动的限制条件,可用于非均匀来流下的三维曲面激波反设计。
2) 基于微元密切轴对称方法分别求解了带攻角来流与外锥形流来流2种来流条件下的标准内锥曲面激波及波后流场,数值仿真结果证实了所设计的三维曲面激波形状与预设形状完全吻合。
3) 该方法为高超声速飞行器三维乘波前体、内转式进气道及二者的气动一体化设计提供了新的解决途径,展示出在该领域内的重要应用前景。
