二维弯曲激波/湍流边界层干扰流动理论建模
2022-10-14程剑锐施崇广瞿丽霞徐悦尤延铖朱呈祥
程剑锐,施崇广,瞿丽霞,徐悦,尤延铖,朱呈祥,*
1. 厦门大学 航空航天学院,厦门 361102 2. 中国航空研究院,北京 100012
激波/边界层干扰(Shock Wave/Boundary Layer Interaction, SWBLI)机理及其流动控制始终困扰着航空航天工程界和学术界。自1940年Ferri首次通过实验观测到机翼后缘的SWBLI造成边界层分离现象以来,有关其流动特性与影响因素就一直被广泛地研究与讨论。尽管SWBLI流动呈现出较强的非定常性,然而构建一种时均的无黏简化模型用于理论描述或分析干扰流场基本特征具有重要意义,譬如Delery等提出经典的入射斜激波/平板湍流边界层干扰无黏简化模型分析方法。但可以发现,以往大多数的流场结构研究更多集中于直线型或以直线为母线的圆锥型激波,然而此类流动模型在曲面构型导致弯曲激波波后流动呈现明显非均匀的情况下似乎难以有效反映出流场特性,即不具备描述一般干扰流场的普适性。以曲面压缩进气道及其反设计为例,弯曲激波/边界层干扰(Curved Shock Wave/Boundary Layer Interaction, CSWBLI)已经逐渐成为不可忽视的流动特征。即便在直线激波的边界层干扰问题中,受流动非均匀性影响,分离激波及反射激波事实上也会呈现出变曲率弯曲的流动特性。
本质而言,CSWBLI属于SWBLI,因此除激波本身外,传统SWBLI的大量研究对CSWBLI仍具有指导性意义。如Chapman等根据大量实验结果提出经典的自由干扰理论(Free Interaction Theory, FIT),将分离原因归结为来流马赫数与雷诺数的影响,这也成为人们研究流动分离的基本定理之一。在后续研究中,学者们通过实验和数值模拟陆续发现了干扰流场受多种因素共同影响,如边界层状态、入射激波强度、下游扰动等。但另一方面,弯曲激波又表现出相较直线激波的特殊性,尤其是沿弯曲激波的不规则参数变化以及波后流场的非均匀性,由此也带来构建CSWBLI流动模型的困难。对于CSWBLI问题的准确描述必须依赖于弯曲激波理论(Curved Shock Theory, CST)的发展与应用。Mölder首次推导出包含涡量变化的非均匀一阶弯曲激波方程组,将波后非均匀参数梯度与激波曲率通过代数方程组联系起来。Shi等在上述工作基础上对方程沿激波求偏导得到二阶弯曲激波方程组以及高阶弯曲激波求解方法,而高阶参数意味着更丰富的流场信息与更高的建模精度。因此,CST的建立为CSWBLI流动模型的构建提供了新的理论方法。
本文以CST为基础,结合FIT构建了二维入射弯曲激波/平板湍流边界层干扰的流动特征模型,通过数值仿真验证了模型的可靠性,并在此基础上应用理论模型分析了弯曲入射激波强度、边界层厚度、下游扰动对二维CSWBLI的影响规律,总结了分离区的增长特性。
1 弯曲激波/边界层干扰理论基础
1.1 弯曲激波理论
有别于直线激波的波后均匀参数,弯曲激波理论建立面临的最大挑战在于如何给出波后各向异性的参数描述,尤其是与波前参数的关联关系。事实上,Mölder和Shi等提出的弯曲激波理论是通过分析弯曲激波曲率和激波前后流动参数导数之间的关系来解析流场的,在三维弯曲激波上建立流动平面与垂流平面,通过定义如图1所示的流向与横向激波曲率和,将复杂三维激波曲面映射于两正交平面(二维流动情况下横向曲率为0)。图中:激波角定义为曲线-相对于入射速度的倾角;为沿-方向的距离;和分别为波前波后的流向角;为流动偏转角。
通过引入3个参数,即标准压力梯度:=(∂/∂)·(),为压力,为流线方向,为密度,为流向速度;流线曲率:=∂/∂;标准涡量:=,为涡量。将其代入流线-垂流线坐标系下的欧拉方程,联立R-H方程(式(1)和式(2)),整理可得一阶CST方程组(式(3))。
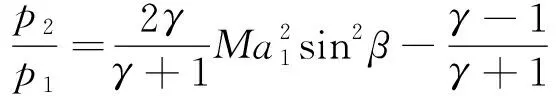
(1)
+sin=+sin(-)
(2)

(3)
式中:为比热比;为马赫数;系数、、、、、、以及带角标“′”的系数均为来流马赫数、激波角、流向角的显式函数;下标“1”和“2”分别代表波前波后参数。详细推导过程较为复杂,具体可参考文献[17, 20]。若沿激波曲线对一阶参数进一步求偏导可以得到二阶乃至更高阶的弯曲激波方程组。其物理意义在于:相较于直接离散弯曲激波求解R-H方程,该理论仅需求解代数方程组即可联系激波曲率得到波后高阶信息,而高阶信息意味着跟踪初始扰动的传播将更为精确。图2中黑色实线为特征线法(MOC)计算结果;蓝色虚线为一阶CST计算结果;绿色虚线为二阶CST计算结果;为来流压力;/表示流场横向无量纲长度。
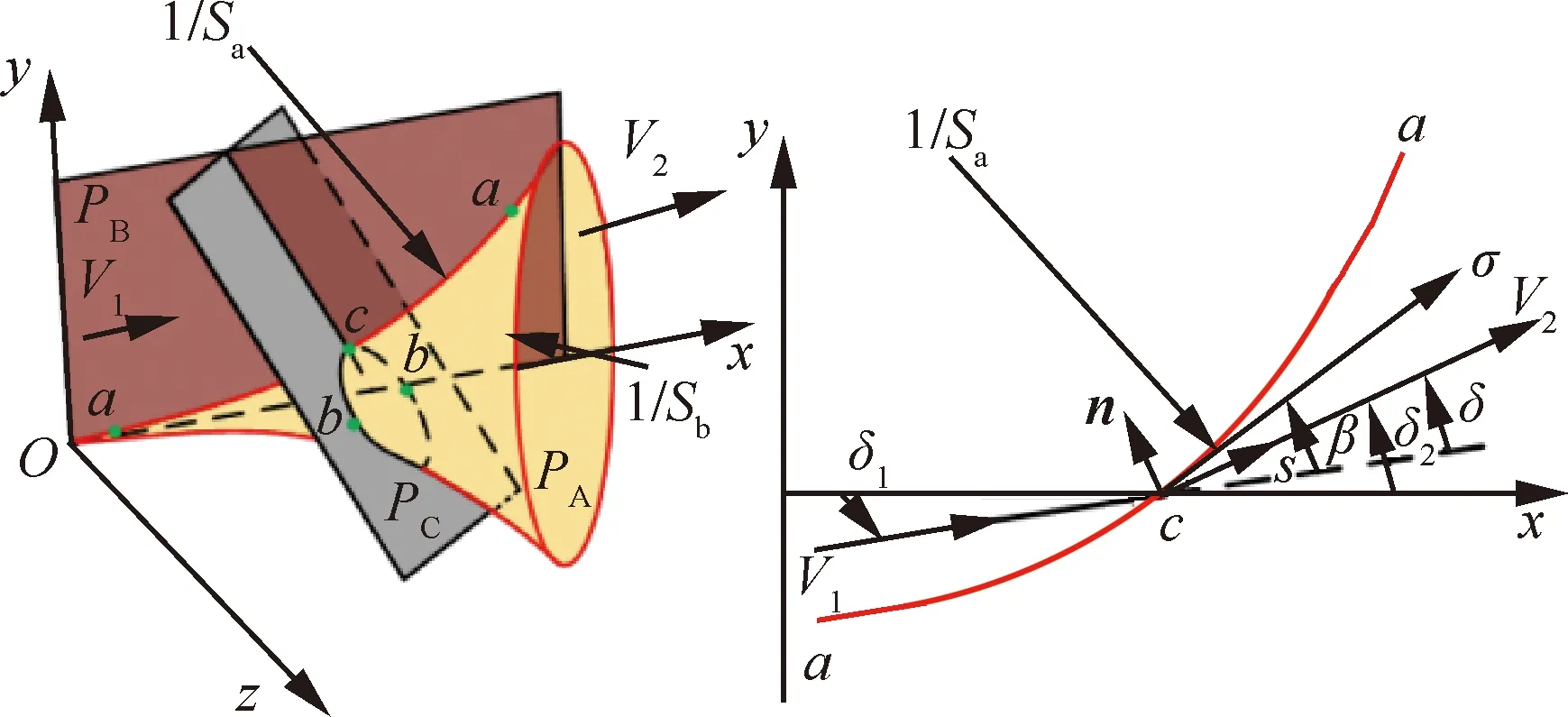
图1 三维弯曲激波几何示意图以及流平面内参数[20]Fig.1 Schematic diagram of geometry of 3D curved shock and variables in flow plane[20]
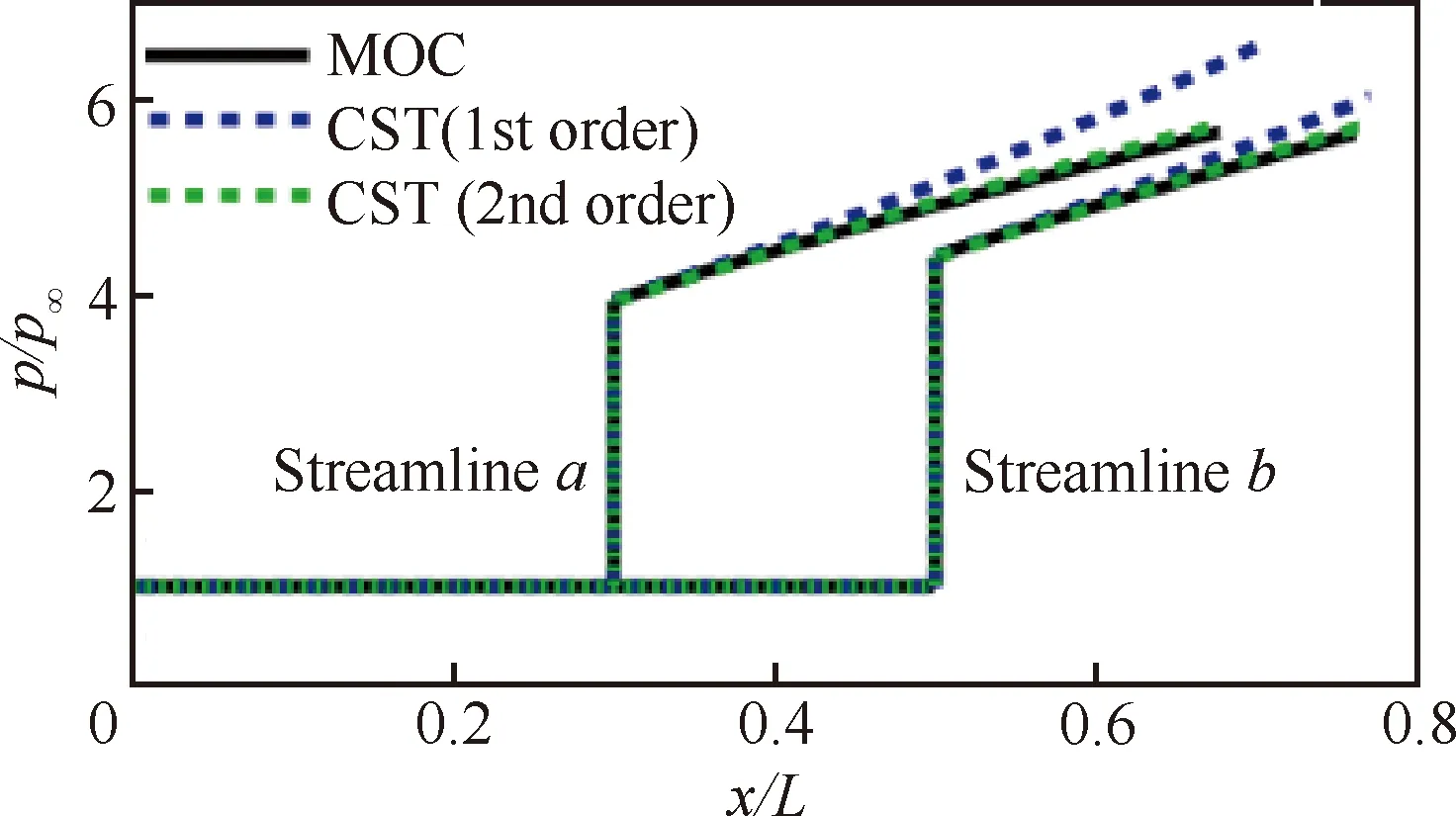
图2 不同方法计算弯曲激波波后沿流线压力分布 (Sa≠0, Sb=0)[20]Fig.2 Pressure distribution along streamlines after a curved shock calculated by different methods (Sa≠0, Sb=0) [20]
1.2 自由干扰理论
自由干扰理论认为,超声速分离是当地边界层与无黏外流间的自由干扰过程,分离区增压比以及干扰长度只取决于干扰起始点流动参数,与下游条件以及激波条件无关。尽管越来越多的研究表明FIT存在一定局限性,但不可否认该理论在对分离点附近的增压预测以及对激波/边界层强干扰大分离的定量描述方面仍然是较为准确的。通过简化分析,在壁面处对边界层动量方程式(4)作积分,其中、分别为、方向的速度分量,为剪切应力。联立超声速等熵流动关系式(5),并对结果进行无量纲化处理,得到干扰过程增压关系式(6)。
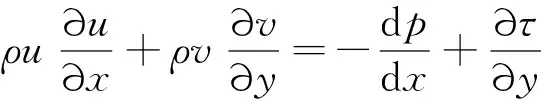
(4)
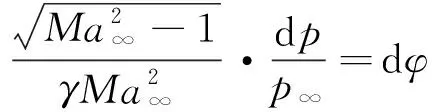
(5)
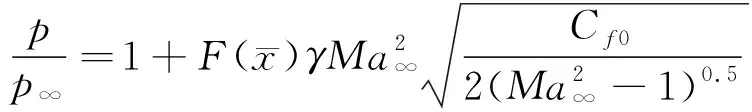
(6)
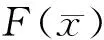
综上,本文将综合应用CST与FIT方法,对在二维条件下弯曲构型的入射激波与湍流边界层相互干扰的流场进行理论流动建模。
2 弯曲激波/边界层干扰理论建模方法
2.1 流场区域划分
CSWBLI与传统SWBLI流场结构相似,主要区别在于激波弯曲带来的非均匀性,尤其体现在入射激波/分离激波发生Ⅰ类Edney干扰后产生的2道透射弯曲激波。图3给出了CSWBLI流动结构示意图。弯曲入射激波与分离激波相交,产生2道透射激波和,激波后流场的非均匀性使得与均表现出弯曲特征。流动穿过激波+与穿过激波+熵增不同,因此从激波交点发出一道弯曲滑移线(剪切层)将两区域分隔开。透射激波与上壁面后端膨胀扇相互干扰,产生弯曲激波′。此外,理论上存在2条特殊流线可将整个流场近似划分为3个区域:流线在穿过入射激波后刚好流经膨胀波与透射激波的干扰起始点,即激波与′的分隔点;流线在穿过分离激波后刚好流经透射激波与分离包的交点,即激波的端点。2条流线将流场划分为区域Ⅰ~区域Ⅲ,其中区域Ⅰ主要流动结构为上游弯曲入射激波压缩与下游弯曲激波/膨胀波相互干扰;区域Ⅱ主要流动结构为弯曲激波/分离激波相互干扰;区域Ⅲ主要流动结构为少部分无黏外流、边界层黏性内流以及边界层分离。
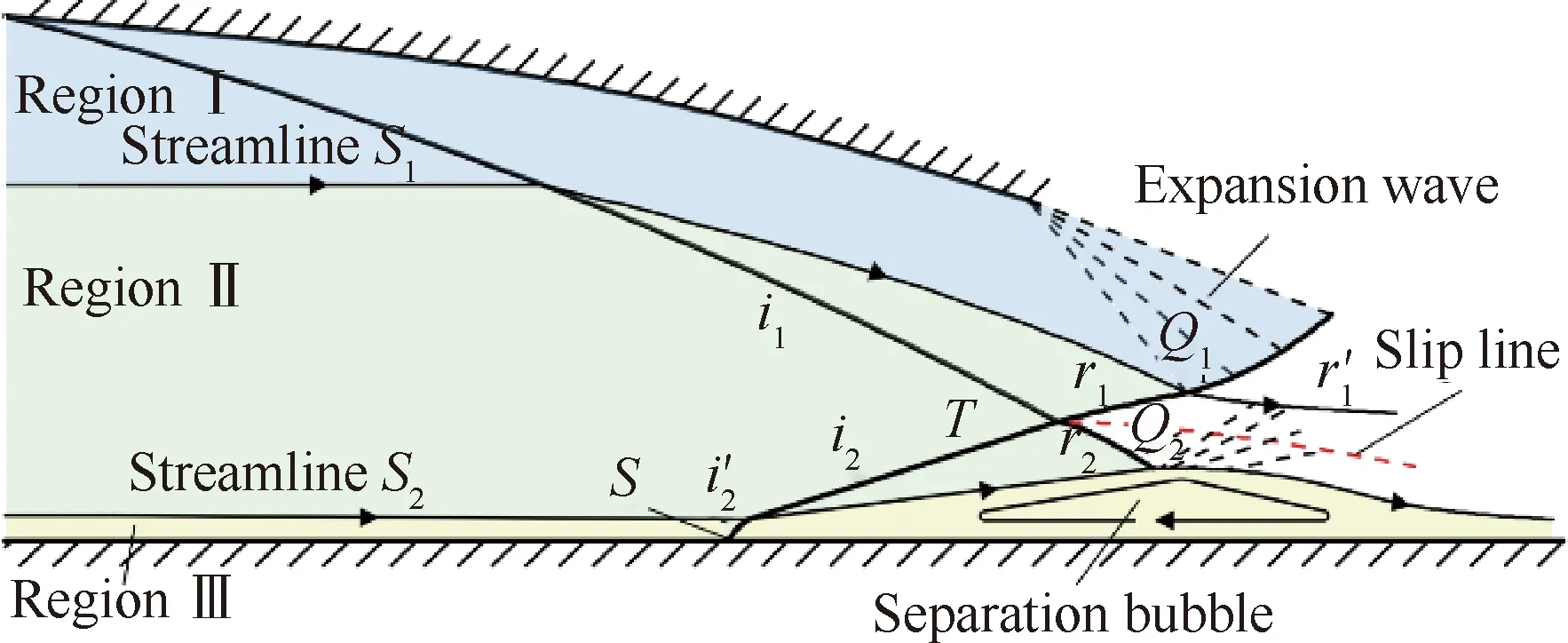
图3 产生分离的弯曲激波/边界层干扰模型Fig.3 Flow model of CSWBLI with separation
2.2 Ⅰ区流动建模方法
对于Ⅰ区流动,上游弯曲入射激波可根据壁面型线由CST方法得到。下游弯曲激波/膨胀波干扰流动特征如图4所示,由于上游入射弯曲激波波后的非均匀性,膨胀波内的马赫线实际为曲线,将弯曲马赫线离散为若干微元段,基于等熵流动假设求解,具体分为膨胀波过程以及激波过程。
在图4(a)所示的膨胀波过程中,EW1为膨胀扇的起始马赫线,其参数可在上游入射弯曲激波波后流场内插值得到。将马赫线离散为若干微元段,每段可近似为直线段,即图4(a)中线段、′,其斜率由马赫波波前流向角和马赫角确定,图中和分别为微元段的局部流向角和局部马赫角。对于从点发出的膨胀扇,沿膨胀角离散为若干微元膨胀扇,且要求流线流经每微元膨胀扇转角相等,由描述等熵膨胀/压缩的P-M方程式(7)求解包括由离散点发出的流线流向角在内的流场参数。流线与马赫线交于点,联立两直线方程可确定点坐标进而求解点流动参数。重复上述过程可逐步解得膨胀扇流场。
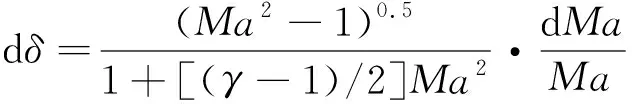
(7)
在图4(b)所示的激波过程中,透射激波′与膨胀波EW1、EW2等依次相交,使得激波′逐渐向上偏转。其中、、分别为微元段的局部压力、马赫数和激波角。由于在膨胀波过程中已得到沿马赫线有关参数,因此激波过程主要通过离散激波,逐步求解激波/马赫波干扰。在图4(b) 中,流线流经膨胀波EW1上半段加激波段与流经激波段加EW1下半段后压力、流向角相等。其中,流经激波参数变化由R-H方程求解,流经马赫波参数变化由等熵流动二阶近似关系式(8)求解,联立此二方程逐步解出激波′的段激波角。此后更新参数,即令马赫线EW1参数更新为马赫线EW2参数,重复上述过程逐步解出透射激波′每一微元段的激波角,进而求解出激波曲线几何形状。

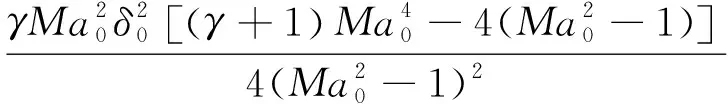
(8)

图4 弯曲激波/膨胀波干扰流动特征Fig.4 Flow characteristic of curved shock wave/expansion wave interaction
2.3 Ⅱ区流动建模方法
对于Ⅱ区弯曲激波/分离激波干扰流动,由于气流穿过激波+与穿过+熵增不同,2个区域被一道滑移线隔开。激波由于波前参数非均匀而呈现弯曲特征,激波尽管波前参数可等效为均匀流场,但由于波后流动受弯曲滑移线两侧复杂流场影响,因此仍然表现出弯曲特征。滑移线两侧的压力、流向角相同,可以通过如图5(a) 所示的-极曲线确定交点的压比以及偏转角:由于在激波交点的气流穿过激波和与穿过和的增压比相同,读取如图5(a)中压比和偏转角即可计算出对应激波角,进而求解该点附近流动状态。对于传统的直线型激波相互干扰,由于波后流场参数均匀,因此交点处流动参数即为干扰区流场的流动参数。然而,对于弯曲的透射激波和,仅获得滑移线起始点位置的坐标(零阶信息)以及激波角(一阶信息)无法得到完整激波曲线。这主要是因为:假设在入射激波上选定若干离散点,, …,进行流线追踪,则当且仅当离散点位于时满足图5(a)中曲线Reg2的激波压缩变化,其他离散点均要首先在激波后经过一段等熵压缩,且离散点越接近交点则压缩距离越短,增压越小,如图5(b)所示。
本质上,-极曲线可认为是对R-H方程的应用,即仅能获取流场参数的零阶信息(坐标值)以及一阶信息(激波角)。但根据1.1节介绍的弯曲激波理论,获取完整弯曲激波的方法需要解析点参数的更高阶信息。因此分别对激波、列出弯曲激波方程组式(9)和式(10),其中下标“11”和“12”表示波前与波后参数,下标“21”和“22”表示波前与波后参数。对于二维平面流动,横向曲率=0。同时,滑移线两侧压力、偏转角处处相等,即压力梯度和流线曲率相等。求解方程组式(9)~式(11),共计6个方程6个未知数,即、、、、、,可以得到、激波曲率和。

(9)
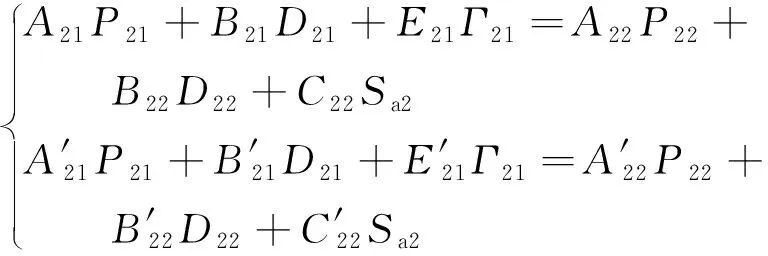
(10)
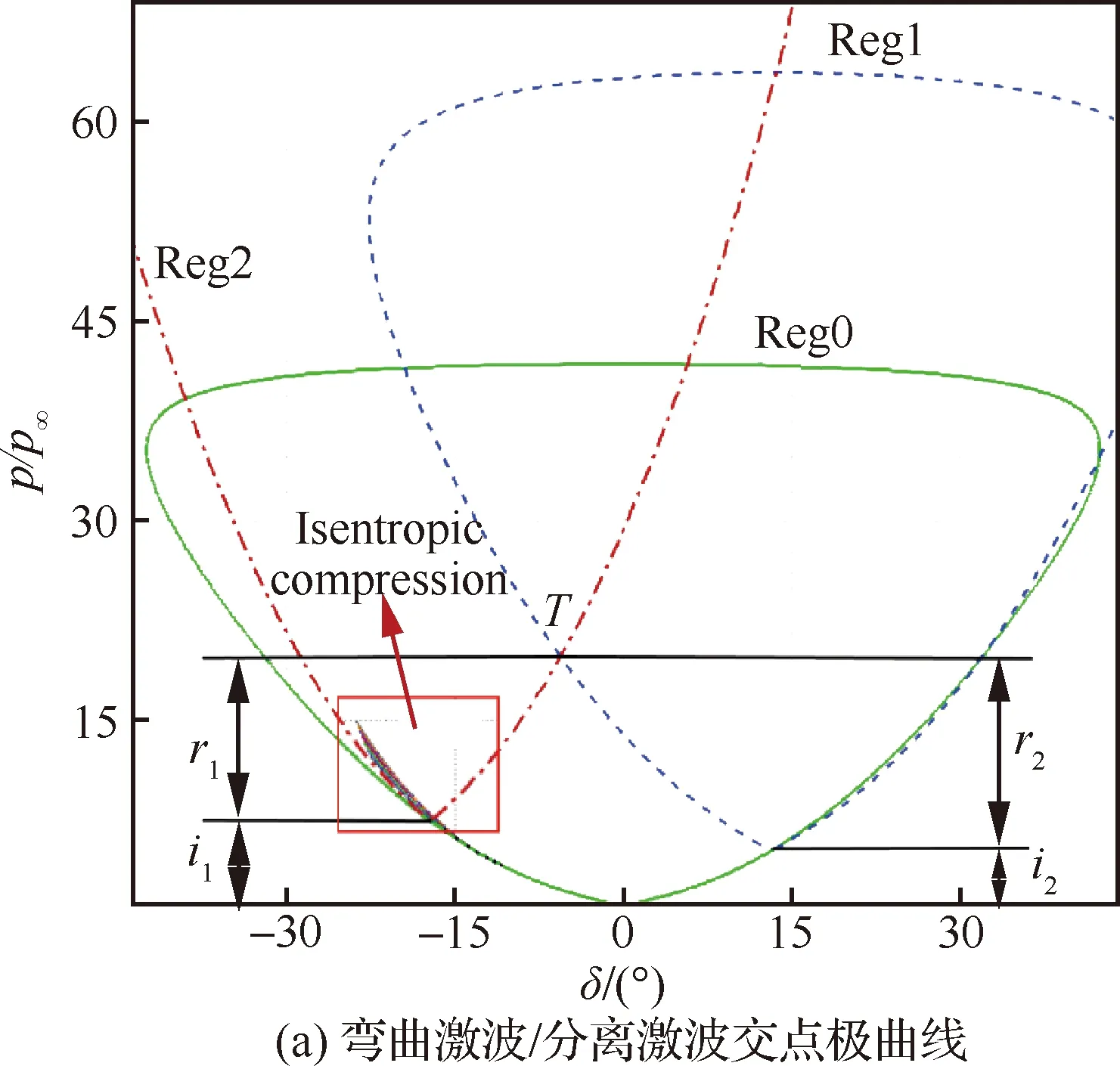
图5 入射激波/分离激波干扰极曲线Fig.5 Shock polar of incident shock/separation shock interaction
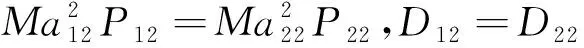
(11)
对于激波的曲线特征而言,激波角相当于描述其形状的一阶参数,即′。曲率相当于描述其形状的二阶参数,即″。在透射激波、交点处作泰勒展开,如式(12)所示,可以得到透射曲线激波坐标(,),下标“=u”和“=d”分别表示点上下侧激波,下标“”表示以点作为展开点。由于与仍处在入射激波与影响域内,因此将激波、曲线离散后在入射激波波后流场内插值即可得到其波前参数,如压力、流向角等。
≈+′(-)+″(-)2=u,d
(12)
2.4 Ⅲ区流动建模方法
Ⅲ区流动涉及湍流边界层的流动近似。分离激波在边界层内与湍流边界层的速度分布相关,法向速度梯度的存在使得该区域分离激波向壁面弯曲,形成长度有限的一段弯曲分离激波′,而弯曲分离激波′的高度及形状取决于当地边界层厚度及速度分布。湍流边界层包含黏性层流层、对数层以及外层,且每层占比受多种因素如雷诺数、压力梯度等影响,本文拟采用表征湍流边界层速度分布的Coles方程来描述边界层内流动,即:
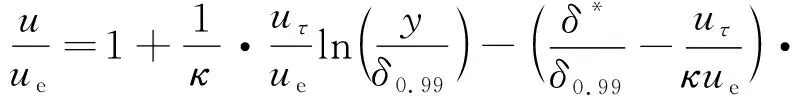

(13)
式中:为边界层厚度;为边界层位移厚度;为边界层外流速度;为摩擦速度且/= (/2),为摩擦系数;= 0.41为von Karman常数;(/)为尾迹分量,并存在以下关系式:
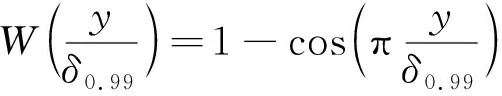
关于湍流SWBLI的分离区尺寸,目前还无法解析地给出其表达式。文献[28-29]指出,无论对于层流还是湍流边界层的分离,其分离区上游影响长度均可表示为几个无量纲特征参数的相关函数:
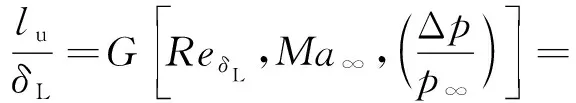

(14)
式中:为上游影响长度,即分离点与无黏激波入射点间长度;为未受干扰时激波入射点的边界层厚度;Const表示常数;、和分别为来流马赫数、压力及以边界层厚度为特征长度的雷诺数;Δ为流经激波的增压值;、、为各项指数,在不同条件下取值不同,对于本文4 ≤≤6、≥10条件,参照文献[28]分别取、、为-1/3、-7/5、4/3。图6反映了式(14) 关于影响长度拟合情况与数值模拟及实验数据的对比,其中黑色实线“Standard line”反映了式(14)左右表达式的函数关系,图中黑色圆点代表本文采用数值模拟方法得到的各算例结果,其余数据点取自文献[28]。由于边界层特性与发展长度紧密相关,因此本节在Ⅲ区流动建模以及后文数值验证中均考虑了一定的边界层发展长度。这一方面可以使得湍流边界层充分发展,另一方面也可以通过控制弯曲激波入射点处的边界层厚度分析其对弯曲激波/边界层干扰的影响规律。
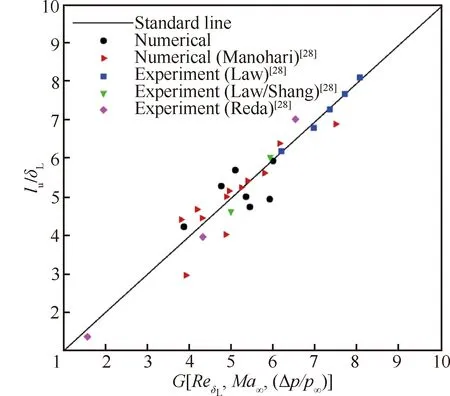
图6 入射激波的上游影响长度Fig.6 Upstream influence length for incident shock
综上,本节建立的CSWBLI理论模型,可以快速预测二维弯曲激波/湍流边界层干扰流场中以弯曲激波相交和分离区等为特征的典型流动结构,CST方法的应用使得弯曲激波波后非均匀流动的求解精度更高,也为弯曲激波/边界层干扰的全流场建模奠定基础。由于Ⅲ区建模依赖于工程拟合以及边界层流动近似,因此将在第3节对该无黏理论模型开展数值验证。
3 CSWBLI模型验证
3.1 数值方法验证
本节将采用数值方法验证第2节提出的CSWBLI模型精度。求解雷诺平均Navier-Stokes方程组,通量项采用二阶迎风格式离散。以结构网格对计算域进行网格划分,并对边界层附近加密。为确保网格无关性,本文分别绘制3套网格,分别为粗糙网格(18万)、中等网格(36万)、精细网格(70万),并设置相同计算条件求解流场。分别提取上述3种网格流场中的壁面压力分布进行对比,结果如图7(图中为流场入口高度)所示,发现采用中等网格与粗网格所得初始升压位置误差约为0.6%,而压力峰值误差为1.8%,由此可以验证网格因素对计算结果影响甚微。综合考虑计算量及计算效率,后文数值模拟过程均采用中等网格对计算域进行划分。

图7 不同网格划分下沿壁面压力分布Fig.7 Pressure distribution along wall with different meshing method
为了选择合理的湍流模型,首先参考文献[16,30]设计了2种斜激波/湍流边界层干扰构型,并分别采用SA (Spalart-Allmaras)、-、-Shear Stress Transport (SST)湍流模型进行仿真,结果如图8(a)和图8(b)所示。对比文献[16,30]中的实验数据可以发现,SA湍流模型对于分离点位置的预测均较其他模型更为准确。事实上,已有相关论述表明,SA模型可以有效反映边界层的黏性影响区,对存在逆压梯度的边界层模拟效果较好,因此本文后续均采用SA模型开展数值验证。
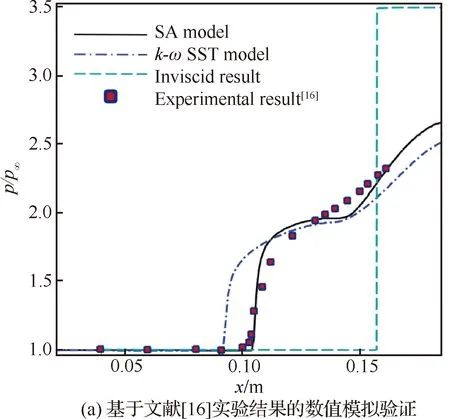
图8 不同湍流模型数值验证Fig.8 CFD verification with different turbulence models
3.2 流场波系结构对比
为了验证CSWBLI理论模型对二维弯曲激波/边界层干扰流动特性的预测精度,本节在不同均匀来流条件下,采用不同二次函数形式给出弯曲壁面构型。为防止该壁面边界层对入射激波型线的干扰,对曲壁面进行无摩擦处理。同时为使平板边界层充分发展,在其上游延伸出一定距离的预发展长度作为远场。参数表示上游预留的平板长度,表示来流入口高度。计算方法及湍流模型同3.1节。对于来流=6,壁面型线=++1,其中=-0.067 8,=-0.191 9,计算所得密度梯度数值纹影如图9所示,其结果与CSWBLI理论模型的定性描述相似,即由弯曲上壁面生成1道入射弯曲激波至下壁面平板边界层引起边界层分离,进而分离区产生一道分离激波与入射弯曲激波相互干扰并形成2道弯曲透射激波。
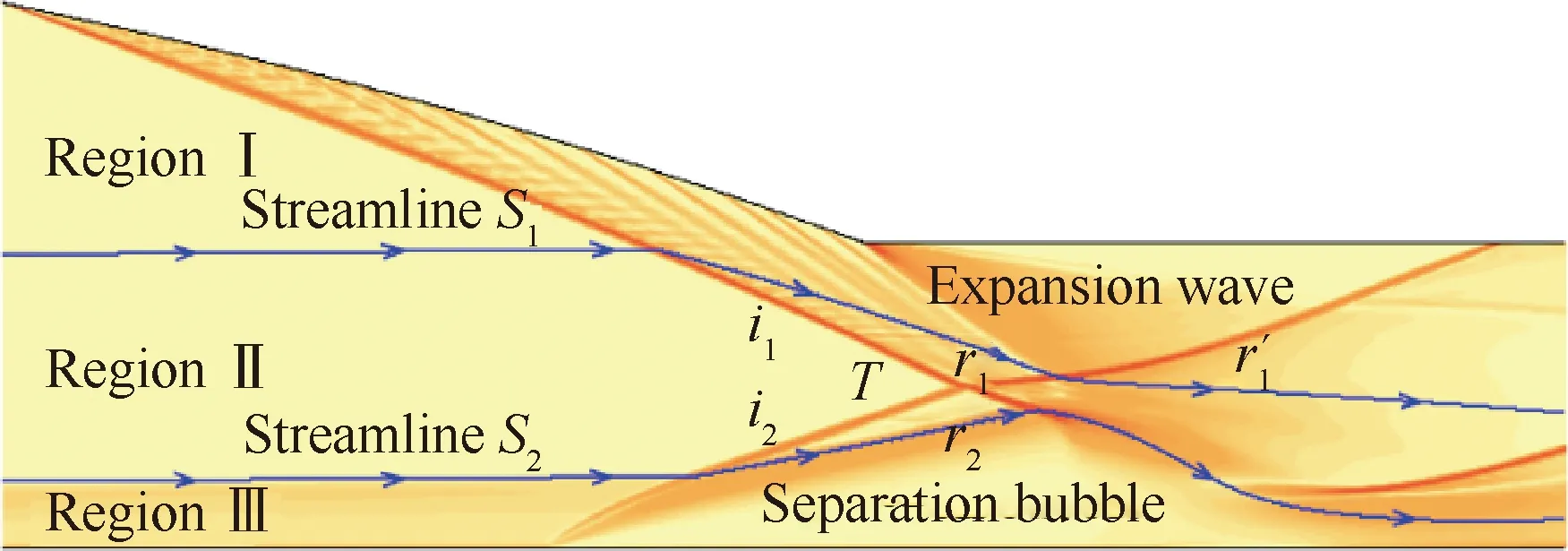
图9 入射弯曲激波/边界层干扰数值纹影(y=-0.067 8·x2-0.191 9x+1, Ma∞=6)Fig.9 Numerical schlieren of incident curved shock wave/boundary layer interaction (y=-0.067 8·x2-0.191 9x+1, Ma∞=6)
本文提出的CSWBLI无黏理论模型着重构建了干扰流动特征,尤其体现在对弯曲激波及弯曲激波干扰结构的有效复现。图10给出了CSWBLI无黏模型理论计算所得各道激波,包括弯曲入射激波、分离激波、透射激波和以及受膨胀波影响的弯曲激波′。图10中黑色点划线表示采用简化模型理论求解的波系,背景云图为采用3.1节计算方法得到的CFD结果。图10(b)和图10(c)分别为边界层分离点、激波干扰点附近局部放大图。图10(a)内各关键点坐标值是在通过CFD方法得到的流场云图中直接读取所得,图10(b)和图10(c)坐标轴上数值表示通过CSWBLI无黏理论模型计算的关键点坐标值。将坐标看作以原点为起点的向量,分别比较理论模型与云图各关键点向量的模与向量角。将各关键点坐标值误差表示在图11(a)中,纵坐标表示理论结果与CFD结果的比值。可以发现,除分离点外,各关键点向量模误差最大值小于0.13%,向量角误差最大值小于2.63%。

图10 CFD结果与理论计算波系对比(y=-0.067 8x2-0.191 9x+1, Ma∞=6)Fig.10 Comparison of shock waves between CFD and theoretical results (y=-0.067 8x2-0.191 9x+1, Ma∞=6)
此外,分别改变来流马赫数、壁面型线参数、上游边界层预发展长度进行理论计算与数值验证,各算例参数条件汇于表1,相对误差情况分别如图11(b)~图11(e)所示。可以看出当参数条件改变时其误差均可保持在较小水平,在算例3的极限情况下最大误差低于4.5%。由于式(14)本身的拟合精度,部分关键点的数值结果与理论结果存在偏离。然而从整体上看,本文所构建的CSWBLI流动模型在给定的范围内能够实现较好的流场重构。

图11 关键点坐标的CFD与理论结果对比Fig.11 Comparison of CFD and theoretical results of coordinates of key points

表1 不同CSWBLI算例参数设定Table 1 Parameter setting in different cases of CSWBLI
3.3 分离区结构对比
3.2节表明CSWBLI理论模型可以有效预测二维弯曲激波/边界层干扰的弯曲激波相交及分离区特征。本节将所预测的分离区结构等效为壁面,并在此基础上结合二维弯曲壁面开展无黏流动数值仿真。作为对比,同步对相同二维弯曲壁面直接开展有黏数值仿真。图12(a)给出了有黏数值仿真和结合CSWBLI理论模型的无黏数值仿真得到的流场结构。可以发现二者流动结构吻合良好,但由于边界层内分离激波′的弯曲特性,理论模型与仿真流场的实际分离点存在一定偏差。若将压力平台处激波沿图12(a)中白色虚线延伸至平板并将其交点定义为名义分离点,可以发现名义分离点与理论模型得到的分离点重合度较高。
为了定量对比2个流场,图12(b)与图12(c)分别提取了流线与流线上压力分布进行对比。其中,图12(a)有黏流场中流线、仍选取为Ⅰ、Ⅱ、Ⅲ区分界线;而在图12(a) 无黏流场内,流线仍为穿过膨胀波初始马赫线与透射激波交点的流线,流线则要求其与分离激波的交点和有黏流场中的交点横坐标相同,即保证在两流场中沿流线的初始压升位置相同。
对比可以发现,图12(a)中有黏和无黏流场的激波及流场云图基本呈现对称分布,说明干扰流场内分离包结构是产生复杂流动结构的主要原因,而本文构建的CSWBLI无黏模型能够有效反映该分离包结构,进而实现对流场波系的重构,即通过无黏流动来复现有黏流动的主要特征。从图12(b)和图12(c)沿流线、压力分布的对比来看,无黏流场可以精准模拟有黏流场的波系位置及激波强度,再次证明了CSWBLI无黏模型的高重构性。
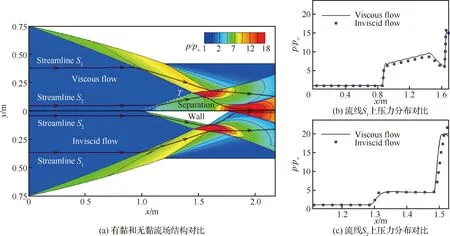
图12 有黏/无黏流场流动结构和无量纲压力分布对比Fig.12 Flow structure and dimensionless pressure distribution comparison in viscous/inviscid flowfield
4 CSWBLI理论模型应用
第3节通过数值方法验证了CSWBLI理论模型,该理论模型无论是对二维弯曲激波/边界层干扰的波系结构还是分离区位置与尺寸均拥有较好的描述。本节将尝试利用该模型对二维弯曲激波/边界层干扰现象进行规律性研究,着重考虑弯曲入射激波强度、边界层厚度、下游扰动3个关键参数对二维CSWBLI流动的影响规律,并在此基础上总结分离区增长特性。
根据1.2节干扰过程增压比方程式(6),压力平台性质主要由来流马赫数、壁面摩擦系数决定。而与边界层性质及发展情况有关,用于描述边界层发展情况的参数可采用当地雷诺数。对于较大的情况,应用von Karman隐式方程求解,即
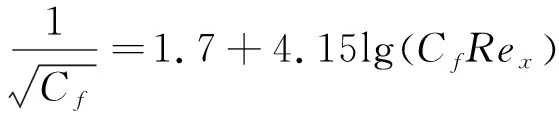
(15)
除此之外,入射激波强度对SWBLI干扰流场也有较大影响。当来流条件一定,斜激波强度可选用激波角表示,但对于激波角沿曲线变化的弯曲激波而言,需要一个能够综合描述整体激波状态的参数来衡量其强度。根据CST方法,来流条件一定时弯曲激波几何条件由壁面曲线形状决定且一一对应。对于二次函数壁面形状=++,系数作为入射激波高度的无量纲基准,令=1,同时令二次曲线对称轴位置-/(2)为常数,此时可提取参数作为衡量壁面形状的唯一几何参数。实际上,对壁面求二阶导得″=2,因此参数可用于描述壁面的弯曲程度。来流马赫数一定时,代表入射激波的值绝对值越大则入射激波强度越高。
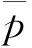

(16)
式中:表示波后速度;为激波曲线。由式(16)可知,波后等效背压实际相当于波后的质量平均压力,代表了下游扰动对于入口激波状态的综合影响。对于本文+的激波相交结构,式(16)扩展为

(17)
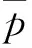
图13表示不同入射激波下,通过控制上游边界层预发展长度来探究激波入射点边界层厚度对分离区尺寸的影响规律。分离区尺寸随入射点边界层厚度明显增长,且激波强度越高则增长幅度越大。由于在CSWBLI理论建模时应用了式(14),因此其增长关系大致满足的2/3次幂。而对于同一边界层厚度条件,入射激波强度越大则分离区尺寸越大。图中= -0.098 4为该入射条件下激波强度的最大边界,若继续增大弯曲激波强度,则入射激波在平板发生正则反射后无法匹配流线转角,即发生马赫反射。

图13 CSWBLI分离上游影响长度随边界层厚度及入射激波强度的变化Fig.13 Variation of upstream influence length in CSWBLI with local boundary layer thickness and incident shock intensity
图14反映不同入射弯曲激波下,固定上游预发展长度,分离区尺寸随波后背压的变化规律。其中黑色点划线为CSWBLI模型适用边界。由图可见,激波强度越大则其可承受背压值越高。在本文设定条件下,当分离激波强度小于入射弯曲激波强度时(即图中||≥0.04),分离区与波后背压值呈负相关。进一步减小入射激波强度,该变化趋势相反,即在较弱入射激波下,分离区尺寸随波后背压而增大。此外,可以发现对于较小强度的入射激波,分离区尺寸对背压的变化更为敏感,下游很小的扰动将造成分离区尺寸较大的改变。
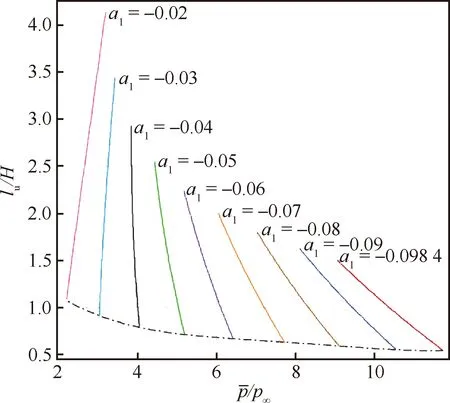
图14 CSWBLI分离上游影响长度随波后反压的变化Fig.14 Variation of upstream influence length in CSWBLI with back pressure
综上所述,本节描述了分离区随入射激波强度、激波入射点边界层厚度、下游扰动的增长规律。本文所建立基于CST方法的CSWBLI无黏模型实际构造了描述弯曲激波与边界层干扰的多元函数,因此以上述影响因子作为输入条件,以干扰流场特性作为输出参数,可以有效分析流场内参数分布规律。
5 结 论
1) 基于Mölder弯曲激波理论,结合经典的自由干扰理论,构建了带有分离的二维入射弯曲激波/平板湍流边界层干扰的初步模型CSWBLI。流场内3个区域采用不同方法加以分析。其中,采用泰勒展开求解弯曲激波/分离激波干扰波系的方法有效克服了极曲线法在弯曲激波特性求解应用的难题。
2) 二维入射弯曲激波/湍流边界层干扰,主要特征在于波后各向异性参数分布。其流动结构包括入射弯曲激波、分离激波、弯曲透射激波、分离包结构。相较于入射斜激波/边界层干扰,CSWBLI中激波呈现出明显弯曲特性。
3) 通过数值方法对比无黏理论模型与黏性干扰流动情况,提取二者关键点位置向量及沿流线压力分布做定量对比。不同条件下流场建模精度不同,最大误差小于4.5%,最小误差趋近于0。因此总体而言理论模型能够较好地实现黏性流场的重构。
4) 建立了以分离点当地边界层厚度、入射激波强度、波后等效背压为自变量,以分离区上游影响长度为因变量的函数关系。在本文设定条件下,分离区尺寸随入射点边界层厚度增加而增长;而分离区受下游扰动影响情况与入射激波强度有关,强度较大的激波有能力承受更高的背压。
