极区格网惯性导航性能分析
2017-06-10彭文生孙付平蔡韧鸣肖乐杰
彭文生,孙付平,蔡韧鸣,肖 凯,肖乐杰
(信息工程大学 导航与空天目标工程学院,郑州 450001)
极区格网惯性导航性能分析
彭文生,孙付平,蔡韧鸣,肖 凯,肖乐杰
(信息工程大学 导航与空天目标工程学院,郑州 450001)
针对传统惯导系统在极区因地理经线快速收敛导致无法精确定位定向的问题,提出一种利用格网坐标系直接获得格网航向进而优化惯导系统导航性能的方法:通过构建基于格网坐标系的导航方程和系统误差模型,重点分析采用格网坐标系的惯导系统在极区能够解决定向问题的原理。仿真结果表明,在极区使用格网坐标系代替地理坐标系作为导航系,能够较好地解决传统惯导系统在极区的定向难题,其姿态、速度和位置3者的误差与传统惯导系统在低纬度地区的误差相当。利用格网坐标系的惯导系统能够满足载体在极区航行的要求。
极区;惯导系统;格网坐标系;误差模型;导航性能
0 引言
随着我国综合国力的增强和海外利益的不断拓展,我国人员、舰艇和飞机的活动范围逐渐覆盖全球,极区精确导航成为必须解决的课题。由于复杂的地理、气候和电磁环境,全球卫星定位系统(global positioning system,GPS)、天文导航、磁罗经等多种导航手段在极区都存在一定程度的缺陷,导航的精度不能得到保证[1-3]。惯性导航由于其能够自主导航,不会受到外界干扰和具有较强的隐蔽性,已成为导航的主要手段。然而传统的惯导系统在极区尤其是近极点区域存在因经线收敛引起的严重定位定向难题和系统误差偏大的问题[4-8]。格网坐标系正是基于解决传统惯导系统在极区的定向难题而提出的一种有效手段。
文献[9]定义了格网坐标系的基本概念,以地理系真北航向为参照,定义了格网北向,并推导了地理北向与格网北向之间的夹角(σ)与地理经纬度之间的关系式。文献[10]从格网坐标系的定义出发,推导了格网系的惯性导航力学编排方程。
本文进一步探讨σ角与地理经纬度之间的关系,着重对格网系能够实现在极区定向的数学机理进行分析,通过构建格网坐标系下的导航方程和系统误差方程研究格网坐标系下的误差模型。
1 格网坐标系的建立
设载体的位置为P,格网坐标系用G表示,其定义为:过P点作一平面平行于本初子午面,同时过P点作当地水平面,2个平面相交产生的交线以北偏东为正向,即格网系G的北向轴,格网天向与地理天向重合,格网东向、北向和天向构成右手坐标系,如图1所示。
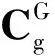

(1)
对北半球而言,文献[11]推导了σ、纬度L及经度λ的关系:
(2)

(3)
2 导航方程
1)位置微分方程

(4)
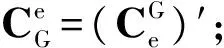

(5)
VG为载体在格网系中的速度。
将球面坐标换算成直角坐标的计算公式为
x=(RN+h)cosLcosλ;
y=(RN+h)cosLsinλ;
z=(RN(1-f)2+h)sinL。
(6)
式中:RN为卯酉圈曲率半径;h为载体高度;f为地球扁率。
2)速度微分方程

(7)
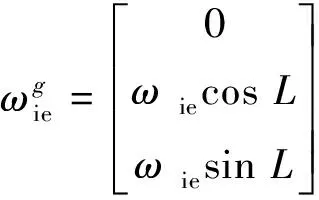
(8)
(9)

(10)
式中:RM为子午圈曲率半径;VGE为格网系东向速度;VGN为格网系北向速度。
3)姿态矩阵微分方程

(11)
综上,可得到以格网系为导航系的总的导航方程为

(12)
3 误差方程及定向机理分析
根据惯性导航系统通用ψ角误差模型[12]230,可得格网系下惯性导航系统的ψ角误差模型基本方程为:
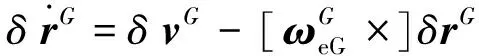
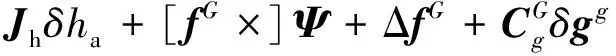
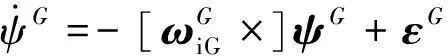
(13)
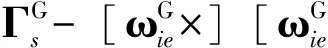
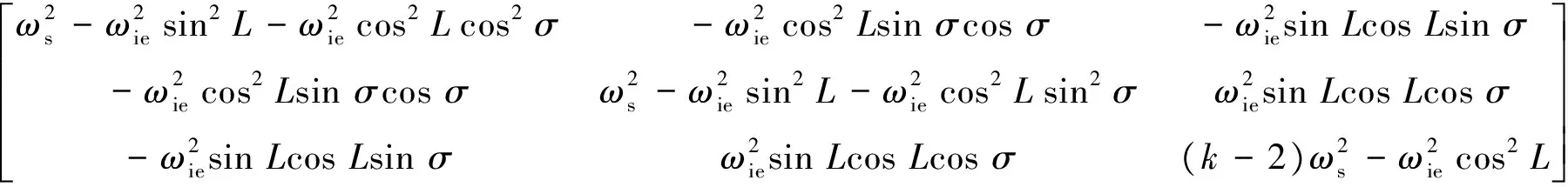
(14)

1)位置误差

(15)
2)速度误差

(16)
3)漂移角误差

(17)
格网系定向机理分析:
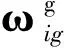
(18)
观察式(18)中的第3项可知,当载体位于极点附近时,天向陀螺的指令角速度接近于无穷大,意味着平台上的力矩器要对陀螺施加无穷大的力矩,而这是无法实现的;因此当载体在极点附近时,平台无法实现稳定跟踪当地地理坐标系,这将对惯导的定位定向产生极大影响。对于捷联惯导,虽然没有实体平台;但是其在解算水平速度时,由于计算式中含有tanL项,当载体位于极点附近时,会引起严重的计算误差,甚至导致计算溢出。
再对以格网系作为导航系的系统进行考察,由式(1)、式(8)和式(9)可得

(19)
观察式(19),不存在当载体位于极点附近时使其值趋近于无穷大的项;因此对于指北式平台惯导,可按照指令角速度正常对陀螺施矩。而对于捷联惯导,在解算水平速度时也不存在计算溢出的问题。
进一步分析,对式(2)及式(3)微分,得
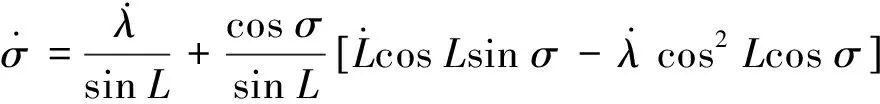
(20)
(21)
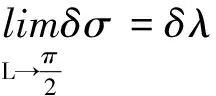
(22)
可见,在载体靠近北极点的过程中,δσ是否发散取决于δλ是否发散,而
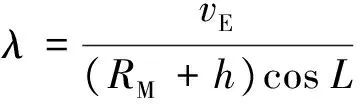
(23)
(24)
从漂移角误差方程可知,航向误差漂移角不存在使方程发生发散的项;因此格网航向是不发散的。由地理航向φN和格网航向φGN的关系式
δφGN=δφN-δσ
(25)
可以看出:在δφGN不发散而δσ发散的情况下,要使等式两边相等,只有地理航向δφN的发散量与δσ的发散量相当;因此可以理解为在格网系的航向角中,由于引入了格网方位角σ,使得地理系的发散量被扣除,从而使得格网系的航向角不发散,保证了格网系较高的航向精度。
4 实验与结果分析
为了验证本文将格网坐标系作为导航系在极区的可行性和正确性,利用惯导轨迹发生器生成2条较为特殊的轨迹:一条是沿着固定经线穿过极点,初始位置为[85°N,113°E,1 000m],记为轨迹Ⅰ;另一条是沿着固定纬度运动,初始位置为[85°N, 0°E,1 000m],记为轨迹Ⅱ。2条轨迹初始速度均为150m/s,仿真时间均为10 000s,整个过程保持姿态水平。

根据轨迹发生器生成的仿真数据,使用格网导航方程对轨迹Ⅰ和轨迹Ⅱ进行仿真解算。为了对比,同时使用常规导航解算方法对轨迹Ⅰ进行仿真解算。解算的误差如图2~图11所示,其中图2~图5是格网系下轨迹Ⅰ的姿态误差、速度误差和位置误差,图6~图8是格网系下轨迹Ⅱ的姿态误差、速度误差和位置误差。图9~图11是地理系下轨迹Ⅰ的姿态误差、速度误差和位置误差。
从图2~图4可以看出,轨迹Ⅰ沿着固定经线穿过极点的过程中,横滚误差和俯仰误差小于30″,航向误差小于4′,速度误差小于1m/s,纬度误差小于1.55m,经度误差小于1m。图4中,由于轨迹穿过极点,采用地理经纬度表示位置信息时在极点附近会产生跳变,跳变的原因是跳变前后2个时刻载体位置分别位于极点的两侧,看起来位置误差变化较大,实质上计算位置与真实位置的几何距离并不大,更直观的解释见文献[13]。如果在解算中不采用经纬度表示位置,而是采用式(6)将经纬度坐标转换成直角坐标,则采用地心地固直角坐标表示位置信息时,解算误差不存在跳变的情况,如图5所示。
从图6~图8可以看出,轨迹Ⅱ在极区绕固定纬度圈运动的过程中,横滚误差和俯仰误差在小于30″,航向误差小于1.5′,速度误差小于1m/s,纬度误差小于0.8m,经度误差小于10m。
图9~图11中的轨迹是截取了轨迹Ⅰ中载体从开始运动至到达极点时的轨迹。从图中可以看出,采用传统地理系解算方法,在载体运动至极点附近时,其航向误差、速度误差和位置误差急剧增大,验证了前文所述。
综合比较格网系轨迹Ⅰ和轨迹Ⅱ的解算误差图可以看出,无论是沿着固定经线穿越极点,还是在极区沿着固定纬度运动,都没有出现传统的惯导系统在极区的误差发散的情况,格网系误差都保持在较小的范围内,说明在极区采用格网坐标系作为导航系具有较高的精度。
5 结束语
在近极点附近,传统惯导系统的航向误差会急剧增大,存在无法定位定向的问题,采用格网坐标系能够比较直观地得到格网航向。本文对格网坐标系进行了研究,推导了格网坐标系作为导航系的导航方程和误差方程,并对格网航向在极点附近不发散的数学机理进行了分析。2组特殊轨迹的仿真结果表明,在极区使用格网坐标系代替地理坐标系,具有较高的导航精度,能够较好地解决传统惯导系统在极区的定向难题;因此在极区使用格网坐标系,在低纬度地区使用地理坐标系,能够实现全球导航。然而,怎样选择2种坐标系的切换时机,使得导航系统性能最佳,仍是一个有待研究的问题。
[1] YAHYA M H,KAMARUDIN M N.Analysis of GPS visibility and satellite-receiver geometry over different latitudinal regions[EB/OL].[2016-05-18].http://eprints.utm.my/7722/1/ISG2008-1.pdf.
[2] GREENSPAN R L.Inertial navigation technology from 1970-1995[J].Navigation,1995,42(1):165-185.
[3] GREWAL M S,WEILL L R,ANDREWS A P.Global positioning systems,inertial navigation,and integration[M].Toronto:Wiley,2007:103-160.
[4] ADAM W.Navigational systems and simulators[M].Gdynia:CRC Press,2011:13-46.
[5] TITTERTON D,WESTON J L.Strapdown inertial navigation technology[M].Herts:IET,2004:17-58.
[6] KENNETH R.Inertial navigation syetems analysis[M].Toronto:Wiley,1971:109-153.
[7] GROVES P D.Principles of GNSS,inertial,and multisensor integrated navigation systems[M].Boston:Artech House,2013:121-195.
[8] BERKIR E.Introduction to modern navigation systems[M].New Jersey:World Scientific,2007:75-85.
[9] IGNAGNI M B.An all-earth inertial navigation scheme[J].Navigation,1972,19(3): 209-214.
[10]周琪,秦永元,付强文,等.极区飞行格网惯性导航算法原理[J].西北工业大学学报,2013,31(2):210-217.
[11]秦永元.惯性导航[M].北京:科学出版社,2014:356-360.
[12]高钟毓.惯性导航系统技术[M].北京:清华大学出版社,2012.
[13]严恭敏.飞越极区导航定位误差跳变的直观解释[EB/OL].(2016-03-13)[2016-11-16].http://blog.sina.com.cn/s/blog_40edfdc90102wms3.html.
Performance analysis of INS in polar region based on grid coordinate frame
PENGWensheng,SUNFuping,CAIRenming,XIAOKai,XIAOLejie
(Information Engineering University, Zhengzhou 450001, China)
Aiming at the problem that the convergence of geographic meridians makes steering and positioning extremely difficult when utilizing conventional inertial navigation system in polar region, the paper proposed a method that uses the grid coordinate frame to get the grid heading angle and enhance the navigation performance of inertial navigation system: the polar grid navigation equation and the system error model were established based on the grid coordinate frame, and the theory that inertial navigation system with grid coordinate frame could determine orientation accurately in the polar region was focused on.Simulation result showed that the orientation problem existed in conventional inertial navigation system could be well solved with the navigation of grid coordinate system instead of geographic coordinate system in polar region, furthermore, the errors of attitude, velocity and position of the proposed method would be equal to those of conventional inertial navigation system in low latitude region, which indicated that the inertial navigation system with grid coordinate frame could fulfill the navigation requirements of polar region.
polar region; inertial navigation system; grid coordinate frame; error model; navigation performance
2016-11-03
国家自然基金项目(41374027)。
彭文生(1985—),男,江西乐安人,硕士研究生,研究方向为惯性导航与组合导航。
彭文生,孙付平,蔡韧鸣,等.极区格网惯性导航性能分析[J].导航定位学报,2017,5(2):38-43,54.(PENGWensheng,SUNFuping,CAIRenming,etal.PerformanceanalysisofINSinpolarregionbasedongridcoordinateframe[J].JournalofNavigationandPositioning,2017,5(2):38-43,54.)DOI:10.16547/j.cnki.10-1096.20170207.
P
A
2095-4999(2017)02-0038-07
