＊WS-RI增量模式回溯的边界收缩加速

翟治年，卢亚辉，周武杰，3，彭艳斌，郑志军，俞 坚，丰明坤

1.浙江科技学院 信息与电子工程学院，杭州310023

2.深圳大学 计算机与软件学院，广东 深圳518060

3.浙江大学 信息与电子工程学院，杭州310027

1 引言

正随着云制造[1]等众包业务模式的发展，更多工作流开始依赖于第三方资源。此类资源通过云平台，以虚拟服务形式接入[2]，容易隐匿恶意，威胁业务安全。为防止恶意资源提供者获取关键数据，须对有关步骤施加授权约束。但其可能破坏资源分配可行性。相应的验证与决策，称为工作流可满足决策（Workflow Satisfiability Decision，*WS）[3]。*WS 属于NP 难问题[4]，仅在少数约束配置[3]或特定约束图规范[5]下多项式时间可解。通常的搜索会因“组合爆炸”产生性能瓶颈。而蚁群等智能算法难以保证完备性，不利于无解判定[6]。一个可能的优化方向是打破对称（Symmetry Breaking）[7]。即分析约束集中的对称因素，避免重复搜索对称不可行解，从而降低验证开销。

2014年，Cohen等识别了多种安全约束的资源独立（Resource Independent）性质[8]。相应约束下的*WS 记为*WS-RI。定义了*WS-RI 的合格（满足所有约束）资源分配模式。相同模式的资源分配合格性等价。为利用这种对称性，建立了借助模式压缩缓存的动态规划算法。其时间复杂度为O*(3||Vwlbw)，式中V是步骤集，w是资源分散度。但其空间复杂度仍为指数级，制约了实际性能表现。2016年，通过约束传播、消除无用资源和预处理，使模式动态规划获得了优化的时间性能[9]。2015 年，Karapetyan 等将模式引入回溯搜索，建立了*WS-RI的模式回溯法[10]。其出发点是在与步骤授权集无关的模式空间上搜索真实、合格资源分配。为此，解决了模式真实性（即该模式是否可能满足授权）的验证问题，方法是计算模式中步骤块到资源集的指派（二分）图，然后求其单向完备匹配。而模式合格性可以根据文献[8]的结论来验证。模式回溯具有多项式空间复杂度，而时间复杂度为O*(B|V|)，其中B|V|为第 |V|个Bell数。起初，仅对叶模式进行充要的真实性验证，而对其祖先仅做必要的快速验证[10]。2018年，翟治年等表明对每个模式进行充要的真实性验证，可以平衡剪枝能力与验证代价，增强宏观性能表现[11]。不过，在验证模式真实性时，文献[11]沿用了文献[10]的做法，从头计算完全指派图并求其匹配。设D表示资源集，一次真实性验证耗时O(|V|2|D|)。但其可能在每一个搜索结点处发生，且 |D|可比 |V|大得多[12-13]，故其3 次多项式的代价仍然偏高。2019 年，Karapetyan 等利用父子模式的差异，给出了增量化的真实性验证方法。一次验证耗时O(|V|2+|V||D|)[14]，降至二次多项式。由此建立了增量模式回溯（Incremental Pattern Backtracking，IPB）的方法。实验表明，相对于包括文献[9]在内的各种代表性方法，IPB 具有突出的性能优势，是目前求解*WS-RI最高效的方法。

模式技术引起了理论和应用上的进一步探索，例如文献[15]在强指数时间假设下，证明模式动态规划时间复杂度的最优性，文献[16]将模式回溯法进行推广，应用于层次化类独立约束*WS的求解等。

本文将对IPB 的真实性验证过程进行改进。针对其计算差异块邻域时，在整个资源集中展开搜索的缺陷，给出了一种边界收缩的加速方法。实验表明，改进方法在时间性能上获得了较明显的提升，且在资源集和步骤集规模较大时更有优势。

2 预备知识

*WS-RI是一个三元组＜V,d,C ＞。其中V是步骤集，d:V→2D是步骤授权集，D是资源集。C是约束集，每个c∈C有作用域Vc⊆V，值域Dc⊆。且|Vc|＞1 ，称为c的元数。对任意资源分配π:V'→D(V'⊆V)，若任取v∈V'，π(v)∈d(v)，称π是授权的。任取约束c∈C，若在Vc上的限制π↑Vc∈Dc，称π满足c。任何c∈C都具有资源独立性，即若π满足c，则对任意的θ:D→D,θ(π)也满足c。称满足所有c∈C的π合格，授权、合格的π有效，完整（即V'=V）、有效的π可行。*WS-RI 求任意一个可行资源分配，或判定其不存在。

V'模式是V'的划分(V'⊆V)。给定＜V,d,C ＞，相应*WS-RI 的任何资源分配π:V'→D都会产生一个V'模式Pπ={π-1(u)|u∈π(V')}，称其为π的模式。任何V'模式P都会产生一个资源分配集ΠP={π:V'→D|Pπ=P}。若任取π∈ΠP都合格，称P合格。若存在授权的π∈ΠP，称P真实。称真实、合格的模式有效、完整（即V'=V）、有效的模式可行。模式空间描述了向空划分逐渐加入步骤，扩展为更大划分的过程。每个新步骤要么放入一个已有划分块，要么形成一个新块。用同一步骤扩展不同划分，得不到同一划分，故模式空间呈树结构。

模式回溯法对模式空间进行深度优先搜索，通过合格与真实性验证加以剪枝，找到可行模式后，将其转换为可行资源分配。模式合格性通常根据约束语义来验证。而模式P的真实性验证分两阶段：计算其指派图BP，再求其单向（从左到右）完备匹配。BP的左侧顶集为P，右侧顶集为D。任取块b∈P和资源u∈D，(b,u)∈E(BP)当且仅当对任何v∈b均有u∈d(v)。将模式中每个块匹配的资源分配给块中所有变量，即可得到一个符合该模式的授权资源分配。

文献[14]的IPB 改进了真实性验证过程。对BP左侧的每个顶点，只计算 |V|个邻点（不足 |V|时完全计算）。当回溯搜索验证模式P的真实性时，其父模式sup(P)已通过验证，求得指派图Bsup(P)及其单向完备匹配Msup(P)。而P 相对其父的差异块bP-sup(P)是唯一的。计算该块的邻域，并沿用其他块的邻域，即可由Bsup(P)得到BP。在求BP的单向完备匹配时，以其他块在Msup(P)中的匹配边集为初始匹配，求一条源自bP-sup(P)的增广路即可。

3 基于边界收缩的块指派算法

图IPB 在搜索过程中频繁进行模式真实性验证。每次都需要计算模式的指派图。其计算效率对算法的整体性能影响很大。对每个模式P，IPB仅计算差异块bP-sup(P)的指派邻域。然而，它是从整个资源集D中寻找bP-sup(P)的邻点。对每个u∈D，为验证是否对任何v∈bP-sup(P)均有u∈d(v) ，需要O(|bP-sup(P)|)=O(|V|) 时间。在很大的D中找一个邻点，验证开销也很大。由于每个步骤v∈bP-sup(P)的授权集d(v)都是分散落入整个D的，寻找一个位于所有d(v)中的资源，可以在D中跳跃进行，减少对无效资源的验证。为此，给出一种基于边界收缩的块指派（Block Assigning via Boundary Shrinking，BABS）算法，其伪代码描述如下（next(d(vi),l)表示d(vi)中大于l的第一个值，不存在时取∞）。

算法1 BABS(b,l,h)

输入：b 为待指派邻点的块，l,h ∈D 是b 邻域的任意下界和上界（设D 上定义有全序关系）。

输出：返回b 在[l,h]之间的 ||V 个邻点（不足时全部返回）。

更新模式P的指派图时，算法1 和文献[14]的IPB一样，仅计算差异块bP-sup(P)的 |V|个邻点，仅当其不足时完全计算。由于每个块的邻域在其为差异块时计算完成，故整个指派图中，块邻域大小均不超过 |V|。而文献[10]和文献[11]的模式真实性验证使用了P的完全指派图）。在单向匹配的存在性上，上述两种指派图是等价的，但文献[14]只是默认使用了这一结论。本文补充其证明如下：根据Hall定理，二分图BP存在左到右完备匹配，当且仅当任取Q⊆P,|N(Q) |≥ |Q|,这里N(Q)=N(b)，而N(b)是b在BP中的邻域。任取块b∈P，若其邻域大小达到 |V|，包含该块的任何Q满足|N(Q) |≥|V|≥ |P|≥ |Q|。此时计算其所有邻点或者恰好 |V|个邻点，对整个BP的单向匹配存在性没有影响。由b的任意性得证。

故此，算法1 和IPB 对BP结构的简化不影响P的真实性验证结果，也不会损失授权剪枝能力。文献[14]的变量排序规则，可以在统计意义上增强约束剪枝能力。不过，本文没有对此作出优化。

用算法1 计算任意块b的邻域，时间复杂度是O(|D||b|)=O(|D||V|)。但其既是寻找仅一个邻点，也是寻找所有邻点的最坏理论代价，很难准确反映实际的邻域计算开销。算法1 利用步骤授权资源的分布边缘和间隙跳跃取值，可有效改善这一计算的实际性能。该算法依赖于外部指定的初始边界l和h。在比较粗糙的情况下，可以将它们取作minD和maxD。下一章将利用IPB的搜索结构，以每个模式处常数时间的代价计算更紧的初始边界。

4 边界收缩增量模式回溯算法

下面给出本文的改进IPB，称为边界收缩增量模式回溯（Incremental Pattern Backtracking via Boundary Shrinking，IPB-BS）。它在搜索过程中以增量方式计算差异块邻域的初始边界，以此为参数调用BABS完成该块的邻域计算。其伪代码描述如下。

算法2 IPB-BS(P,&B,M) //递归函数

输入：模式P；传址的二分图变量B=BP；M 是B 的单向完备匹配。初始调用置P ←∅，B ←∅，M ←∅。

输出：返回＜V,d,C ＞的可行解，或其不存在时，返回UNSAT

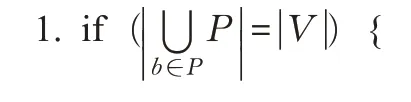
return M ；// M 可视为V →D 映射

} else {

计算将v 加入P 形成的合格模式集X(P,v)；

for (P'∈X(P,v)) {//X(P,v)是用步骤v 扩展模式P可能得到的所有子模式

if (bP'-P={v}) {//v 单独成块。bP'-P表示模式P' 相对其父模式P 的唯一差异块，其中必含步骤v

将d(v)中的前 ||V 个（不足时取全部）指派给bP'-P，将B转换为B' ，并备份更改；//B 可视为P →2D映射，为P 中每个块确定一个指派邻域

lbP'-P←min d(v)；//设置下界初值，lbP'-P是块bP'-P的指派邻域下界

hbP'-P←max d(v)；//设置上界初值，hbP'-P是块bP'-P的指派邻域上界

} else {//P' 是将v 加入P 中原有块而形成的，bP'-P∈P'在P 中对应的块为bP'-P-{v}

if (lbP'-P-{v}∈d(v)) lbP'-P←lbP'-P-{v}；//v 加入前的下界仍然有效

else lbP'-P←next(d(v),lbP'-P-{v}) ；//下界失效，用d(v)中大于lbP'-P-{v}的第一个值对其进行修正

if (hbP'-P-{v}∈d(v)) hbP'-P←hbP'-P-{v}；//v 加 入前的上界仍然有效

else hbP'-P←prev(d(v),hbP'-P-{v})；//上界失效，用d(v)中小于hbP'-P-{v}的第一个值对其进行修正

调用BABS(bP'-P,lbP'-P,hbP'-P)计算bP'-P的邻域，将B 转换为B'，并备份更改；

从M 中删去bP'-P所关联的边；

}

以M 为初始匹配，用Hungary算法求B'的最大匹配M'；

if (| M' |= |P'|) {// M'是B'的单向完备匹配π ←IPBBS( P',B',M' )；

if (π ≠UNSAT) return π；

else {利用备份恢复B；}

} else {利用备份恢复B；}

}//for

return UNSAT；

}

在搜索时，IPB-BS 对每个当前模式相对父模式的差异块进行判断（第7 行）。若其为新步骤单独形成的块，直接设置初始下界和上界（第9 和10 行）。否则，利用新步骤的授权资源集，对差异块的下界和上界加以修正（第12～15行）。这部分工作只需常数时间，不影响真实性验证的时间复杂度。同时，IPB-BS改用BABS计算块邻域，但其时间复杂度仍为O(|V||D|)。BABS 依赖于一些全局性索引数组，可以多项式时间预计算，不占用搜索时间。故IPB-BS 的整体时间复杂度和IPB 一样，为O(B|V|(f(|C|)+|V|2+|V||D|)) ，其中f(|C|) 是 |C|的函数，表示单结点处的约束验证代价。特别地，单结点处的真实性验证代价仍为O(|V|2+|V||D|)。IPB-BS为实现边界收缩附加的全局和局部数据均只占用多项式空间，因而整体上和IPB一样，具有多项式空间复杂度。

5 实验研究

本章将IPB-BS与MPB[11]、IPB[14]等国内外新近工作对比。用C++实现各算法（统一采用IPB的变量排序规则，求匹配增广路时采用宽度优先方式），编译运行环境是：GNU C++、24 GB RAM 的CentOS 7 虚拟机、3.4 GHz Intel Core i3 CPU。单个实例执行时间上限为30 min。

实验1 本实验采用文献[11]的二元随机模型生成仅含互斥约束的测试实例。其参数有 |V|、资源比例μ%=|D|/|V|、约束密度ω%=2|C|/(|V|(|V|-1)) 和授权比例k%=|d(v)|/|D|(v∈V)。它主要通过授权比例的变化来制造困难实例的生成机会。取10 ≤ |V|≤100可以覆盖大多数工作流的步骤集规模，50 ≤μ≤200 反映普通的资源比例，10 ≤ω≤25 反映工作流应用约束密度较低的特点。然后以不同跨度和分布，生成4组k值区间（第1 组：[1，33]、[17，49]、[34，66]、[50，82]、[68，100]；第2组：[8，27]、[24，43]、[41，60]、[57，76]、[75，94]；第3 组：[1，5]、[21，25]、[41，45]；第4 组：[2，4]、[22，24]、[42，44]），每个区间随机生成50 个实例，共800 个实例。三种算法在四组实例上的运行结果如表1所示。

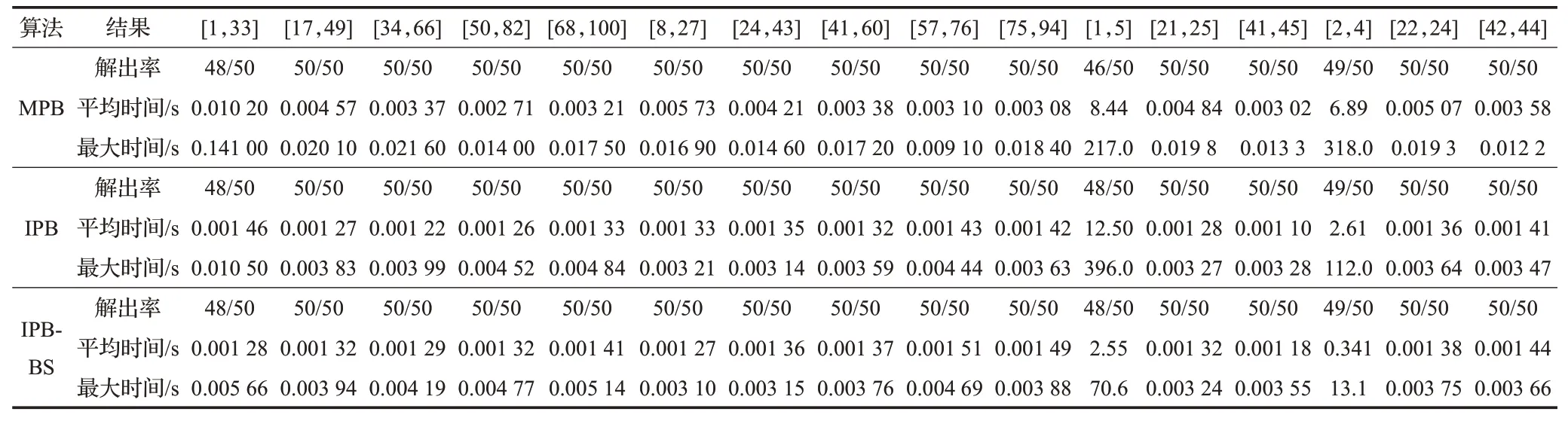
表1 三种算法四组实例结果统计

除第3组的[1，5]区间以外，三种算法在各区间的解出率均相同。在[1，5]区间，两种IPB较MPB多解出了2个实例，解出率高了4%。在所有区间上，两种IPB的未解出实例都相同，且其中不存在MPB 的解出实例。这表明两种IPB 较MPB 有微弱、确定的解出率优势。在各算法都完全解出的13个区间上，IPB的平均时间性能是MPB 的2.93 倍（各区间上平均时间之比的平均值），IPB-BS 是MPB 的2.56 倍。在其余3 个区间（第1 组的[1，33]、第3组的[1，5]和第4组的[2，4]）的共同解出实例上，IPB的平均时间性能是MPB的9.69倍，而IPB-BS是MPB 的35.9 倍。可见在共同解出实例上，两种IPB 较MPB有显著的时间性能优势。这主要因为对于每个当前模式，两种IPB 无需计算每个块的完全邻域，而只需计算差异块的邻域，且至多计算 ||V个邻点，消除了重复计算，并进一步减少了计算的邻点个数。在完全解出的13个区间上，IPB的平均性能是IPB-BS的1.03倍，但在其余3 个区间的共同解出实例上，IPB-BS 的平均性能是IPB 的4.57 倍（在[1，33]区间为1.14 倍，[1，5]区间4.90倍，[2，4]区间7.65倍）。出现这种反差的原因在于：IPB-BS为了实现边界收缩，预先计算了若干索引数组，但其降低了搜索阶段指派邻点的计算代价。对于前13个区间搜索很快完成的实例，IPB-BS 的预计算负担可能使其较IPB 处于劣势，但对于后3 个区间搜索相对耗时的实例，IPB-BS就表现出了自己的优势。特别地，取得了高达4.57倍的性能优势，其原因有两点：首先，测试实例中仅含互斥约束，其检查非常高效，使得真实性验证代价以及指派图计算开销对整体性能产生了更大的影响。进而，这3个区间（特别是[1，5]和[2，4]）的步骤授权比例很低。IPB在原始的资源集中搜索指派邻点，需要检查可高达数十倍的无效资源。IPB-BS避免了这种不必要的代价，从而获得了很高的性能收益。

实验2本实验将采用文献[14]的相变实例生成模型，将两种IPB作进一步对比，探究IPB-BS的其他适用条件。该模型具有更高的资源比例，通过约束数量的调节来生成困难实例。每个实例包含互斥、五元at-most-3和五元at-least-3三种约束。其参数有 |V|、|D|、at-most-3/at-least-3 约束数γ和互斥约束数e。令 |V|从18 开始增加。将资源比例μ取作10和100，以反映第三方资源环境的特点。该模型对每个u∈D，从V中随机选择1～|V|/2 个不同的授权步骤。这将使得授权比例k%≈1/4。at-most-3/at-least-3约束不如绑定/互斥约束常见，故只取γ=|V|。然后根据有解概率恰为50%（即欠约束和过约束两种易解情形中间的位置）的实例难度相变要求，通过估计和验证，确定剩余参数e的值。每组参数都生成了100 个实例，其中有/无解的数量相当，均为理论上的困难实例。将对每组参数下的实例运行结果分有/无解情形取平均值，消除随机性影响后，观察参数变化的性能影响。若出现超时实例，不再计算该组参数下的平均值。同时停止实验，不再求解更大参数的实例。

先在μ=10 的实例集上运行两种算法。每种算法在有/无解情形下，执行时间随 ||V值变化的对数坐标曲线如图1。

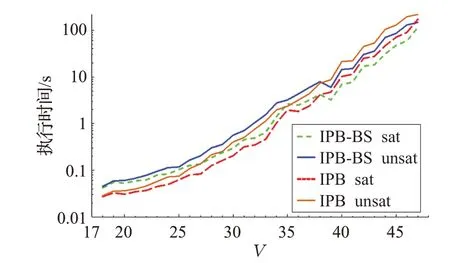
图1 IPB-BS与IPB执行时间对比(μ=10)

每种算法在无解实例上求解性能，通常都弱于有解实例。这主要是因为无解时必然遍历解空间。在|V|=18～38 区间，IPB-BS 处于相对劣势。这主要是因为IPB-BS 的预计算以及边界维护代价。但是，对作图数据的统计表明，由此导致的IPB-BS绝对劣势很小，在有/无解情形下平均差距仅为0.17 s 和0.31 s，最高差距仅为1.55 s。从 |V|=39 开始，不论有/无解情形，IPB-BS都开始取得优势：较IPB平均降低了32.8%的时间代价；最多降低了33.9%，出现在有解情形 |V|=46 处；最少降低了31.6%，出现在无解情形 |V|=39 处。整体上，随着|V|的增大，IPB-BS 不仅开始表现出相对优势，而且其优势逐渐扩大。这是因为两种IPB 的单结点真实性验证时间为O(|V||D|)=O(10|V|2)，而在本实验配置下的约束验证时间为O(|V|2)，前者会随着 |V|增加更快增长，在总代价中占据更高的比例。而IPB-BS 在真实性验证中较IPB 具有优势。当 |V|增加时，这种优势随着真实性验证代价所占比例的提高，得到了更明显的表现。就绝对差距而言，在 |V|=39～47 区间，在有/无解情形下，IPB-BS 较IPB 平均减少了16.9 s 和29.3 s 的执行时间，最高差距达到71 s。

进一步扩大资源比例，对μ=100 的情形进行实验，结果如图2所示。

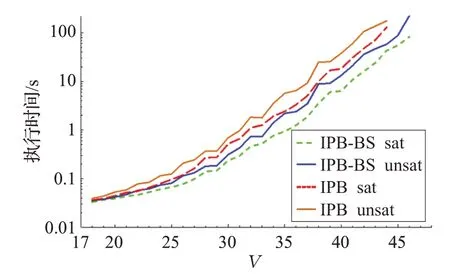
图2 IPB-BS与IPB执行时间对比(μ=100)

此时，IPB-BS的性能优势更为明显。在时限内，较IPB 多计算了 |V|=45 和 |V|=46 两组实例。在 |V|=18～44 区间，相对于IPB，在有/无解情形下平均降低了45.7%和48.7%的时间代价。在有解情形下：最多降低了66.5%的时间代价，出现在 |V|=44 处；最少降低了6.0%，出现在 |V|=19 处。在无解情形下：最多降低了67.0%的时间代价，出现在 |V|=44 处；最少降低了10.6%，出现在 |V|=18 处。相对于μ=10 的情形，IPB-BS不仅取得了更大优势，而且在不同的 |V|处始终处于优势。这主要是因为：本组实例的原始资源集D扩大了10 倍，使得从D中搜索邻点的IPB，其真实性验证代价相对于约束验证代价，以及辅助的初始和维护代价，所占比例更为突出，从而IPB-BS 在真实性验证上的优势表现得更为充分。

6 结论与下一步工作

本文对*WS-RI 的新近算法IPB 进行优化，给出了一种基于边界收缩的加速方法。利用步骤授权资源的分布边缘和间隙，通过边界对齐和滑动的方式，逐步找出步骤块各指派邻点，加快了模式真实性的验证过程。在随机实例集上的实验表明，本文提出的IPB-BS 算法较非增量模式回溯法优势显著。并且对如下的常见应用条件，较IPB有比较明显的性能优势：（1）工作流应用典型的低约束密度，结合此时容易导致困难实例的低授权比例，以及能够高效验证的约束类型。该条件下IPB-BS较IPB具有可高达数倍的性能优势。授权比例越低，优势越明显。（2）第三方资源环境下典型的高资源比例，结合适当的授权比例，以及可导致相变的、适当类型和数量的约束。该条件下IPB-BS较IPB具有比较明显的性能优势。且资源比例越高，步骤数量越多，优势越明显。下一步将对块邻域缓存的设计利用进行研究。